靶機拖帶誘餌飛行對性能影響分析
李紅泉
(中國人民解放軍92419部隊,遼寧興城 125106)
經歷了數十年的發展,無人機技術已經相當成熟,廣泛應用于社會諸多領域,成為表現最活躍的航空產品之一[1],特別是執行超越生理極限的機動飛行或惡劣氣象、生化采樣等極危險任務,具有獨特優勢[2]。軍事方面,由于在中東戰爭中的出色表現,各國軍隊紛紛發展攻擊型無人機,使其擔負大量的作戰任務[3],但平時,無人機更多用在部隊軍事訓練上,或用于驗證各種防空武器的技術性能,于是催生了無人機的一個重要分支——靶標的進步。靶標是一種動態實物航空模擬器,是防空武器所要攻擊目標的替代物,用于防空武器的研制性試驗、鑒定、效能評估,以及部隊訓練和演習[4]。鑒于現在作戰飛機已經發展到第四代,為檢驗第四代戰斗機作戰性能,滿足空戰訓練,為防空部隊防御第四代戰斗機的導彈提供目標,應開展研制相應性能的靶機[5]。
一款先進的靶機不一定都是新研產品,受研制經費、研制周期、可靠性的限制,推出新型號的過程相當漫長,且還要擔負失敗的風險,因此,各國普遍在成熟產品上進行升級改造衍生出新型號的方法,比如美國的石雞/火蜂靶機,先后服役幾十年、十多個型號、近十萬架,陪侍了幾代航空武器。本文提及的導彈形的流線體拖曳誘餌的主要結構參數,以具有一定尺寸和掛裝能力的大型渦噴靶機作為研究對象,采取飛行器設計的通用方法[6-8],進行靶機掛載拖曳誘餌性能分析,計算釋放誘餌之后靶機參數變化,開展使用靶機模擬作戰飛機實施拖曳誘餌[9]干擾的預先研究,為靶機功能升級做前期論證工作。
1 計算內容與基本假設
掛載、釋放并拖帶誘餌飛行,勢必造成靶機性能的變化,主要計算五個方面的影響。
1)釋放誘餌后,靶機的速度變化;
2)釋放誘餌后,需要多大的升降舵偏角,可使靶機繼續水平飛行;
3)釋放誘餌后,靶機的迎角變化;
4)釋放誘餌后,需要多大的方向舵偏角,可使靶機繼續沿航向飛行;
5)釋放誘餌后,靶機的偏航角變化。
為降低計算復雜程度,設計靶機的兩端翼尖均加裝拖曳誘餌(或外型配平),保持整體對稱布局。飛行過程忽略了部分擾動的影響,并作合理假設,分別是:
1)靶機在釋放誘餌之前保持穩定的平直勻速飛行狀態;
2)釋放過程緩慢穩定,忽略釋放造成的動態響應;
3)釋放過程及釋放之后無突風;
4)假設釋放誘餌后發動機推力無變化;
5)纜繩呈直線狀態,質量不變;
6)忽略飛機自動增穩系統的作用。
計算中建立地面坐標軸系、機體坐標軸系、氣流坐標軸系及穩定性坐標軸系,坐標系遵循右手定則和轉換方法,迎角、側滑角由機體坐標軸系定義,拖曳體阻力系數、摩擦系數、靜導數等經驗值取自參考文獻[10]中導彈類飛行器的圖表數據。
2 計算方法
2.1 模型參數及符號定義
計算所需靶機的主要模型參數有:機翼面積、翼展、氣動弦長、起飛重量、推重比、升阻比、縱向及航向操縱導數等;拖曳誘餌的主要模型參數有:直徑、長度、纜長、纜徑、誘餌重量、升阻比、表面摩擦系數等。使用的符號定義見表1,靶機拖帶誘餌飛行示意見圖1。

表1 符號定義

圖1 靶機拖帶誘餌飛行示意
2.2 速度變化
從靶機升阻比求出釋放誘餌后系統的阻力系數,根據阻力計算公式求出穩定拖帶的飛行速度。
由阻力公式和升阻平衡關系,靶機阻力

(1)
式中,CD1為釋放誘餌后系統總的阻力系數,包括四部分,即
CD1=CDtow+CDline-fri+CDline-pre+CDb
(2)
式中,CDtow為誘餌阻力系數;CDline-fri為纜繩的摩擦阻力系數;CDline-pre為纜繩的壓差阻力系數;CDb為靶機阻力系數。
根據導彈類飛行器數據選取誘餌升阻比,則

(3)
(4)
式中,Cfe為等效表面摩擦系數,Set為纜繩外露面積。

(5)
式中,CDcylinder為圓柱體在該雷諾數下的阻力系數。

(6)
再由式(1)、(2),計算出釋放誘餌后速度。
2.3 配平所需升降舵偏角
將誘餌和纜繩作為一個整體進行受力分析,誘餌和纜繩的重力和阻力合并計算,已知誘餌和纜繩阻力之和為
纜繩與水平面間夾角

(7)
纜繩拉力

(8)
根據纜繩與靶機的作用點距離靶機重心之間的縱向距離DX,計算俯仰力矩
Mm=F×sinθ×DX
(9)
由俯仰力矩系數

(10)
最后求得升降舵舵偏
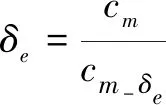
(11)
2.4 迎角的變化
迎角
(12)
計算的數值結果表示釋放誘餌后,如果不改變舵偏,靶機迎角增加情況。
2.5 配平所需方向舵舵偏
根據翼展長度和機身直徑,計算纜繩作用點距離靶機重心之間的橫向距離DY。
偏航力矩
Mn=F×DY
(13)
偏航力矩系數

(14)
方向舵舵偏
(15)
根據計算結果,可知靶機沿原航向飛行需要施加的方向舵舵偏量。
2.6 靶機側滑角的變化
側滑角

(16)
結果表示釋放誘餌后,靶機將向左偏航(釋放左翼誘餌)角度。
3 算例分析
輸入擬拖帶誘餌飛行的靶機主要模型參數和設計的誘餌系統主要模型參數,按照前述方法可計算出靶機翼尖拖帶誘餌對其性能影響結果,對比防空武器的靶標要求,論證靶機模擬作戰飛機實施拖曳誘餌干擾的情況。
根據飛機典型飛行環境,選取靶機在H=8 000 m、V=250 m/s,H=8 000 m,V=200 m/s,H=10 000 m、V=250 m/s,即相同高度、不同速度和相同速度、不同高度三種工況下靶機拖帶誘餌飛行的狀態變化。計算結果見表2。

表2 不同工況的性能比較
分析表2中數據可知:
1)隨著飛行高度的降低,飛行速度變化量明顯增大,而靶機姿態所受的影響變化不大,因此應在高空高速飛行;
2)隨著靶機飛行速度的降低,飛行速度變化量明顯減小,靶機姿態所受的影響變化不大,呈微增趨勢;
3)速度、航向姿態和方向舵偏角的變化較大,主要是由拖曳系統的阻力引起,而纜繩阻力在所有增加的阻力中占的比重最大,這是由于纜繩的外形造成后方流動分離現象嚴重,壓差阻力較大;
4)俯仰姿態和升降舵偏角的變化較小,主要是因為纜繩與靶機的連接點距離重心的縱向距離近,俯仰力矩較小。
4 結束語
與理論計算相比,科研人員還普遍使用專業軟件進行飛行器設計工作,但軟件需要建立三維模型并有限元劃分,對從業者的專業水平和數據處理設備要求較高。對于成熟飛行器的設計改造,利用已有的模型參數,使用本文介紹的計算方法,可以快速得出結果數據;若使用Matlab等運算軟件,僅修改個別參數就可以進行批處理計算,較為便捷,適合于設計的最初階段。
靶機在基本型上衍生改造,也是一種迭代調整優化過程。研究大型靶機模擬拖曳干擾的可行性,需保持系統可靠性,定型的靶機不宜在外形結構上進行大的改變;主要考慮靶機最大載荷條件下,允許的飛行包線,在可接受范圍內,逐步增大拖帶誘餌的尺寸,從而增加干擾功率和欺騙性能,往復計算中找到最優設計方案。另外,文中介紹的計算方法均有通用性,對其他飛行器的設計改進工作或可提供某些參考。

