常用經驗模型預測煤屑瓦斯解吸量對比分析*

張憲尚

(1.瓦斯災害監控與應急技術國家重點實驗室，重慶 400037；2.中煤科工集團重慶研究院有限公司，重慶 400037；3.四川大學，四川 成都 610065)

0 引言

研究煤屑瓦斯解吸擴散特征，對于探索煤礦井下瓦斯涌出、預測煤與瓦斯突出、煤層瓦斯賦存參數測定及煤層氣產能預測等方面具有重要實際意義[1-4]。國內外學者針對不同條件煤屑瓦斯解吸特征進行大量試驗研究并總結得到不同的經驗模型，如Barrer[5]依據甲烷氣體分子在天然沸石中解吸規律試驗研究，提出表達氣體累計解吸量和時間關系的巴雷爾式；Airey[6]研究碎煤瓦斯解吸擴散規律，得到艾黎經驗公式；Bolt等[7]對試驗研究不同變質程度煤的瓦斯放散過程并總結出博特式；孫重旭等[8]認為累計瓦斯解吸量與時間成冪函數關系;王佑安等[9]將煤樣解吸環境快速降至真空，總結得到出王佑安經驗表達公式;宋世釗[10]在譯著中介紹了前蘇聯的研究煤中瓦斯解吸量與時間關系的烏斯基諾夫式。

以上經驗模型是根據不同試驗條件和分析角度得到的，存在一定適用范圍并可以在一些特定環境下相互轉化[11-12]。如巴雷爾公式在地勘期間硬煤取芯推算瓦斯損失量方面得到廣泛應用，但卻不適于構造煤的瓦斯損失量的推算[13]；艾黎式明顯低估了瓦斯解吸開始階段的放散量[11]。根據瓦斯放散量與時間關系及公式特點，這些經驗模型大致可分為冪函數式和指數式2大類，冪函數則被認為煤樣暴露后60 s內的瓦斯放散速度理想的公式[14]。在實際應用過程中，多利用這些經驗模型擬合瓦斯累計解吸量隨時間的變化數據并都表現出較高的擬合度，但對各個經驗模型擬合后瓦斯累計解吸量的預測方面關注較少。

本文在試驗測定煤屑瓦斯累計解吸量的基礎上，取初期不同時間段瓦斯累計放散量數據擬合得到經驗模型參數，將模型參數代入到經驗模型中計算出不同時間的瓦斯解吸量，并將其結果與試驗測定值進行對比。該研究對經驗模型在煤的瓦斯涌出及煤層氣產能預測方面有著重要實際意義。

1 煤屑瓦斯累計解吸量的試驗測定

1.1 試驗樣品

試驗樣品采取寧夏汝箕溝礦3號煤層335工作面煤樣，按標準破碎、篩分成粒度1～3 mm的質量100 g樣品備用。樣品的密度、工業分析及瓦斯等溫吸附參數見表1。

表1 試驗樣品的工業分析及等溫吸附參數

1.2 試驗設備

煤屑瓦斯的解吸擴散屬于一種傳質過程，該過程受煤屑周圍氣體壓力、環境溫度及煤屑內部孔裂結構特征等因素影響，其測定方法一般主要分為重量法和容量法2種，重量法是根據吸附劑(煤屑)解吸前后質量變化測定得到解吸量，而容量法則根據解吸前后固定體積氣體壓力的變化測定解吸的大小[15]。試驗系統主要是由法國Setaram公司研制的全自動siverts型高壓氣體吸、解吸分析儀PCTPro-evo組成，試驗系統實物如圖1所示。

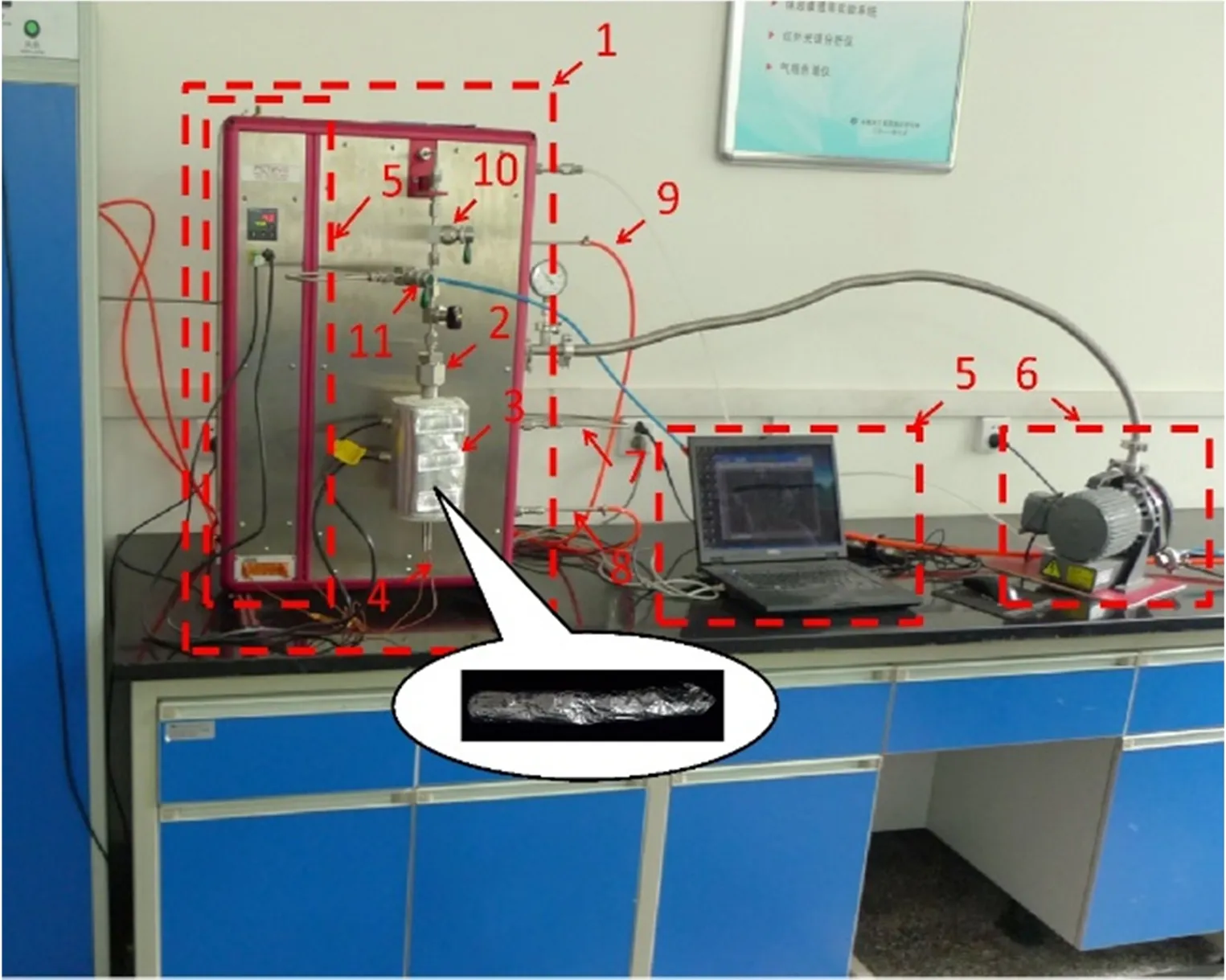
1-PCTPro-evo儀器；2-試驗樣品池;3-加熱套;4-熱電偶;5-數據采集及控制系統;6-干式真空泵;7-甲烷氣體氣路;8-氮氣氣體氣路;9-氦氣氣體氣路；10-閥門；11-閥門。圖1 PCTPro-evo吸附解吸試驗系統Fig.1 PCTPro-evo adsorption and desorption test system

1.3 試驗步驟及結果

1)將待測煤樣取30 g左右，用高精度電子稱詳細稱取煤樣質量并記錄，利用錫紙包裹裝入樣品池中并連接儀器，裝好加熱套等。

2)開啟真空泵，開啟吸附解吸測定儀，對儀器進行自檢及氣密性檢測。

3)氣密性檢測合格后，設定溫度達到60 ℃進行抽真空6 h以上。

4)設定吸附溫度為30 ℃，待儀器溫度穩定后，進行自由空間校準。

5)設置吸附壓力，并設置吸附平衡判別標準。

6)樣品吸附平衡后，關閉閥門10，對儀器進行解吸測定設置，將參考罐中氣體壓力設定為大氣壓壓力。

7)開啟閥門11，放空2 min模擬鉆取煤樣的暴露過程，關閉閥門11，開啟閥門10，進行瓦斯解吸累計量測定，如圖2所示。

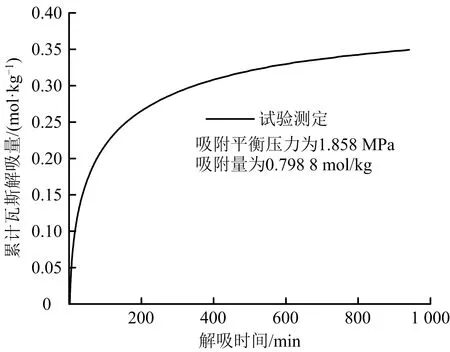
圖2 累計瓦斯解吸量Fig.2 Cumulative amount of gas desorption

8)瓦斯解吸測定完成后，關閉測試軟件及儀器設備。

2 經驗模型擬合

2.1 經驗模型回歸擬合分析

對于含有瓦斯的煤屑解吸放散過程，在煤屑暴露瞬間，只是煤屑外面附近的瓦斯開始涌出。隨著時間的增長，煤屑深部的瓦斯也開始運移，瓦斯運移界面逐漸縮小，瓦斯流動通道長度增加，運動阻力增大，當瓦斯流場長度達到煤屑半徑后，煤屑中心的瓦斯壓力將相應地降低。因此，瓦斯煤屑中的放散速度隨著時間的延長而降低，描述這一衰減過程的經驗方程有[12]：巴雷爾式、撫順式、重慶式、博特式、艾黎式、文特式、烏斯季諾夫式、指數式、模擬近似式等。對于特定煤樣，在其吸附解吸環境一定的情況下，當時間趨于無窮時，其瓦斯解吸量是恒定的，因此在實際的擬合過程中，不同公式的形式可以轉化成相同的擬合形式，如文特式與重慶式。由于試驗測定是煤屑暴露后的瓦斯解吸量，因此需要考慮暴露期間的瓦斯損失量，故擬合公式中出現常數項，并選取暴露時間后解吸5，10，30，60 min的數據，利用origin軟件對其進行擬合得到不同經驗公式的參數值，詳見表2。

2.2 回歸擬合過程及效果分析

利用origin軟件采用Levenberg Marquardt算法對瓦斯累計解吸量隨時間變化的數據進行回歸擬合分析，其經驗公式回歸分析得到的各個參數受到迭代初始值的限制，因此對同一經驗模型回歸分析過程中需要設置初始值時，保持初始值一致或按照參數隨時間變化設置。

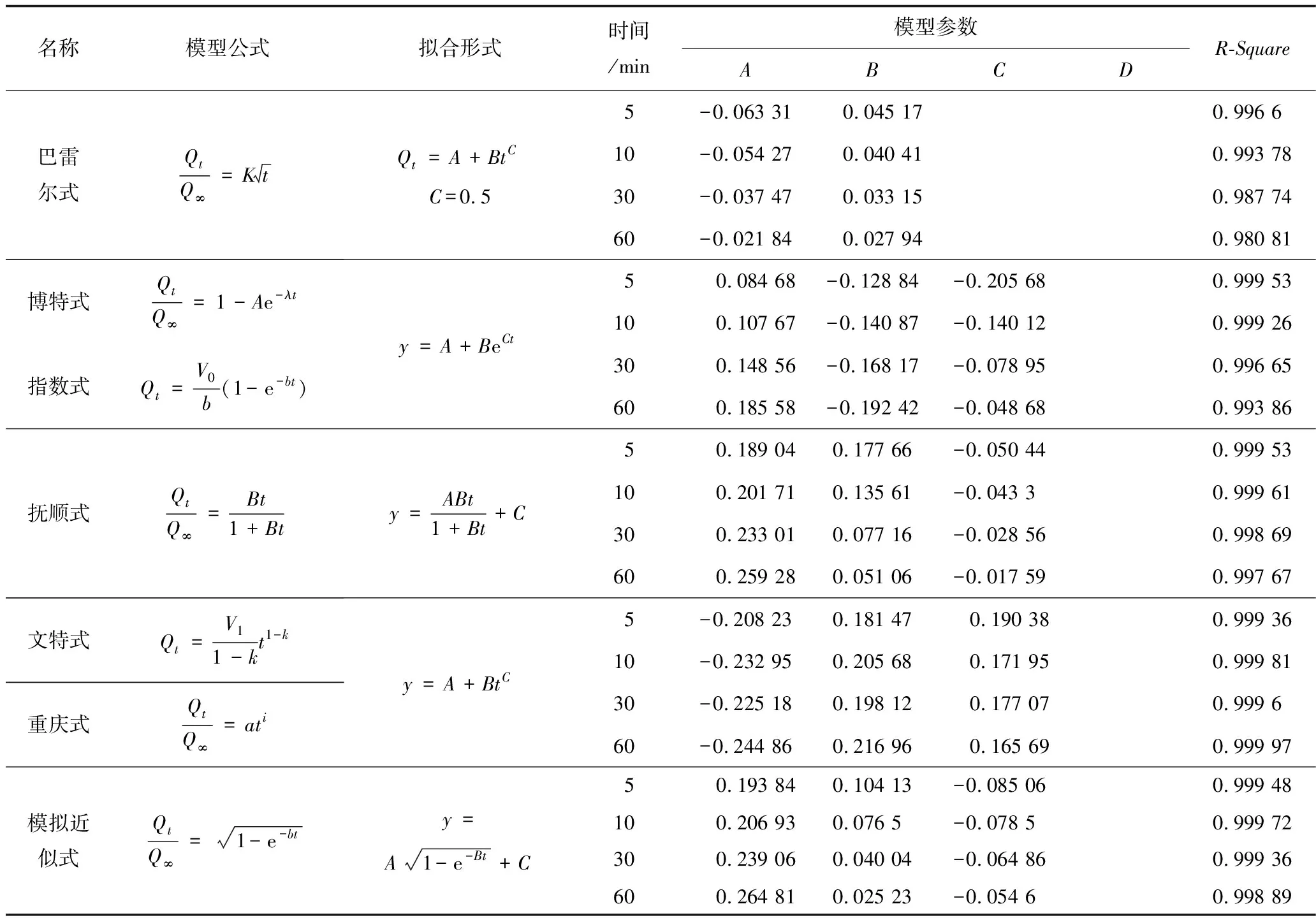
表2 各經驗模型公式擬合參數值

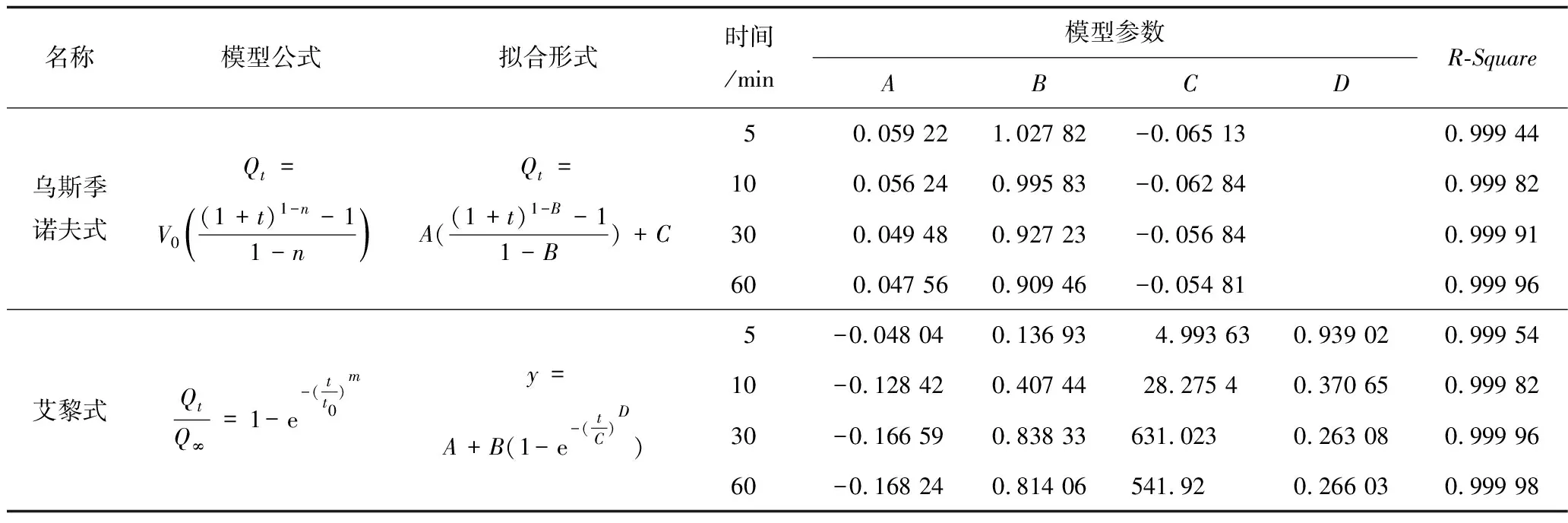
表2(續)

從確定系數R-Square(詳見圖3)值大小可以看出[16]，不同公式擬合過程中確定系數都接近1，表明模型公式的變量對數據解釋能力較強，模型對數據擬合效果也較好，其擬合效果好劣程度依次為：巴雷爾式<博特-指數式<撫順式<模擬近似式<重慶-文特式<烏斯季諾夫式<艾黎式。隨著采取數據時間段的增加，重慶-文特式、烏斯季諾夫式及艾黎式的確定系數R-Square變化平穩，擬合效果不會隨著數據多少而發生變化，而其他經驗模型公式隨著數據的增多而減低，其中巴雷爾式降低尤為明顯。

3 瓦斯解吸量預測對比

為了分析不同經驗模型公式對煤屑瓦斯解吸的預測能力，分別取不同時間段模型參數值代入經驗公式得到不同時間的累計瓦斯解吸量，并與試驗測定值進行對比，如圖4所示。

從圖4中可以看出，巴雷爾式明顯高估擬合時間段后的累計瓦斯解吸量，不適合對累計瓦斯解吸量進行預測，而指數型經驗模型曲線在擬合時間段后很快趨于平直，而低估擬合后累計瓦斯解吸量；對采用5 min和10min時間段的數據擬合參數的各個經驗模型中，烏斯季諾夫式及重慶式都表現出較高的瓦斯解吸量預測能力，這與文獻[17]結論相一致，特別是5 min時間段數據擬合參數的烏斯季諾夫式，但從初期的累計瓦斯解吸量對比中可以看出烏斯季諾夫式明顯高估了煤屑瓦斯解吸量，期間預測能力表現不如重慶式；對30 min和60 min時間段的數據擬合參數的各個經驗模型中，重慶式及艾黎式都表現出較好的瓦斯解吸量預測能力，特別是艾黎式在長期的累計瓦斯解吸量中有較好的預測能力。

圖3 不同時間段數據回歸分析的確定系數Fig.3 Determination coefficients for regression analysis of data in different time periods

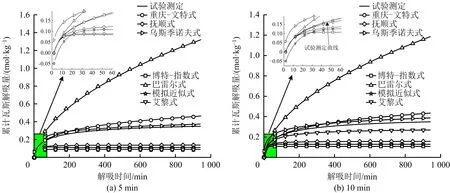
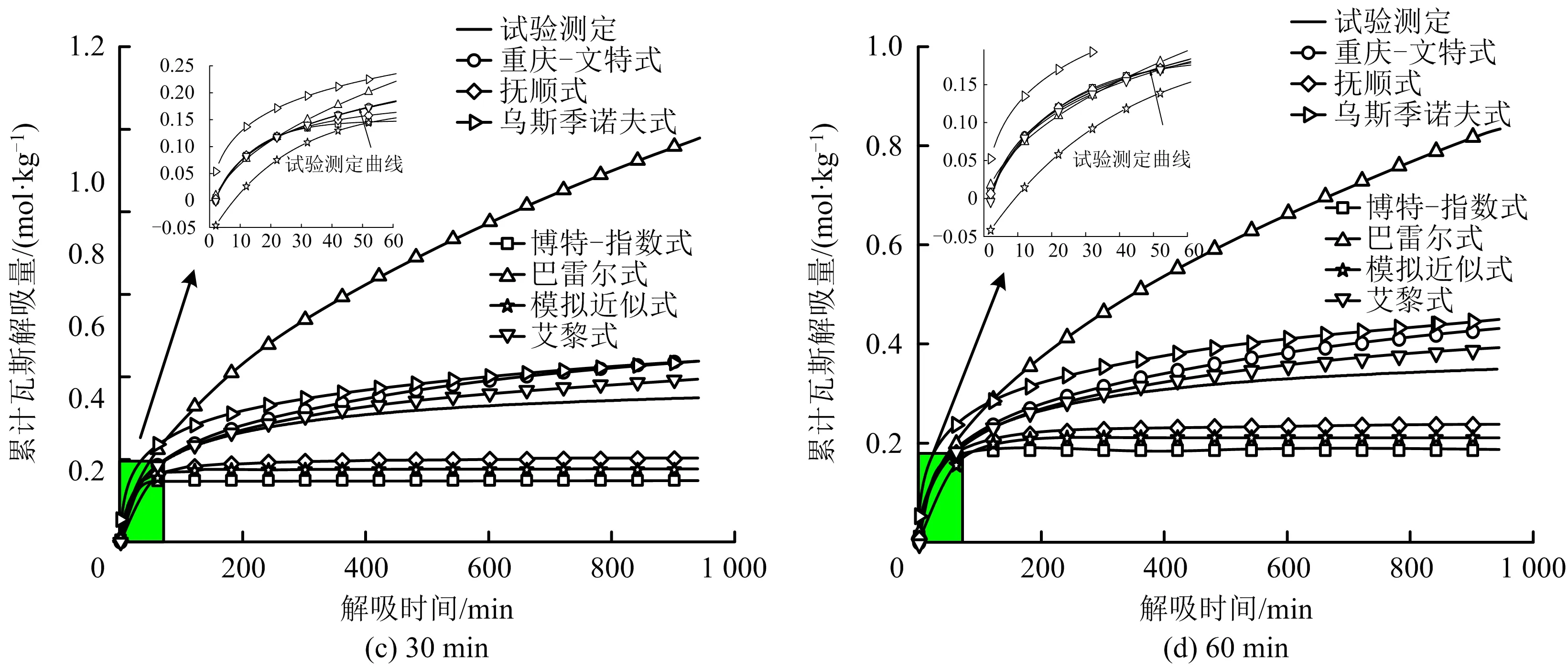
圖4 經驗模型公式瓦斯解吸量預測與對比Fig.4 Prediction and comparison of gas desorption amount based on empirical model formulas

為分析不同時間段數據量對經驗模型的預測能力影響規律，特選博特-指數式、艾黎式、烏斯季諾夫式及重慶-文特式不同時間段擬合計算得到的曲線與實際試驗測定曲線進行對比，如圖5所示。

隨著瓦斯解吸數據時間段的增長，博特-指數式、艾黎式及重慶-文特式計算得到累計瓦斯解吸量曲線越來越接近于實際測定得到瓦斯解吸量曲線，而烏斯季諾夫式隨著瓦斯解吸量數據時間段增長而遠離實際測定曲線，其中博特-指數式和烏斯季諾夫式會隨著時間段延長呈現出規律性接近或遠離。隨著時間段的增長，對于各個經驗模型計算得到曲線而言：博特-指數式在擬合時間段后很快趨于穩定平直，低估煤屑長期瓦斯解吸量，這與指數衰減的擬合形式有關；艾黎式接近實際測定曲線速度最快，在長時間段瓦斯解吸數據預測累計解吸量表現最好；在利用較短時間煤屑瓦斯解吸量數據預測長期瓦斯解吸時，烏斯季諾夫式表現最好。

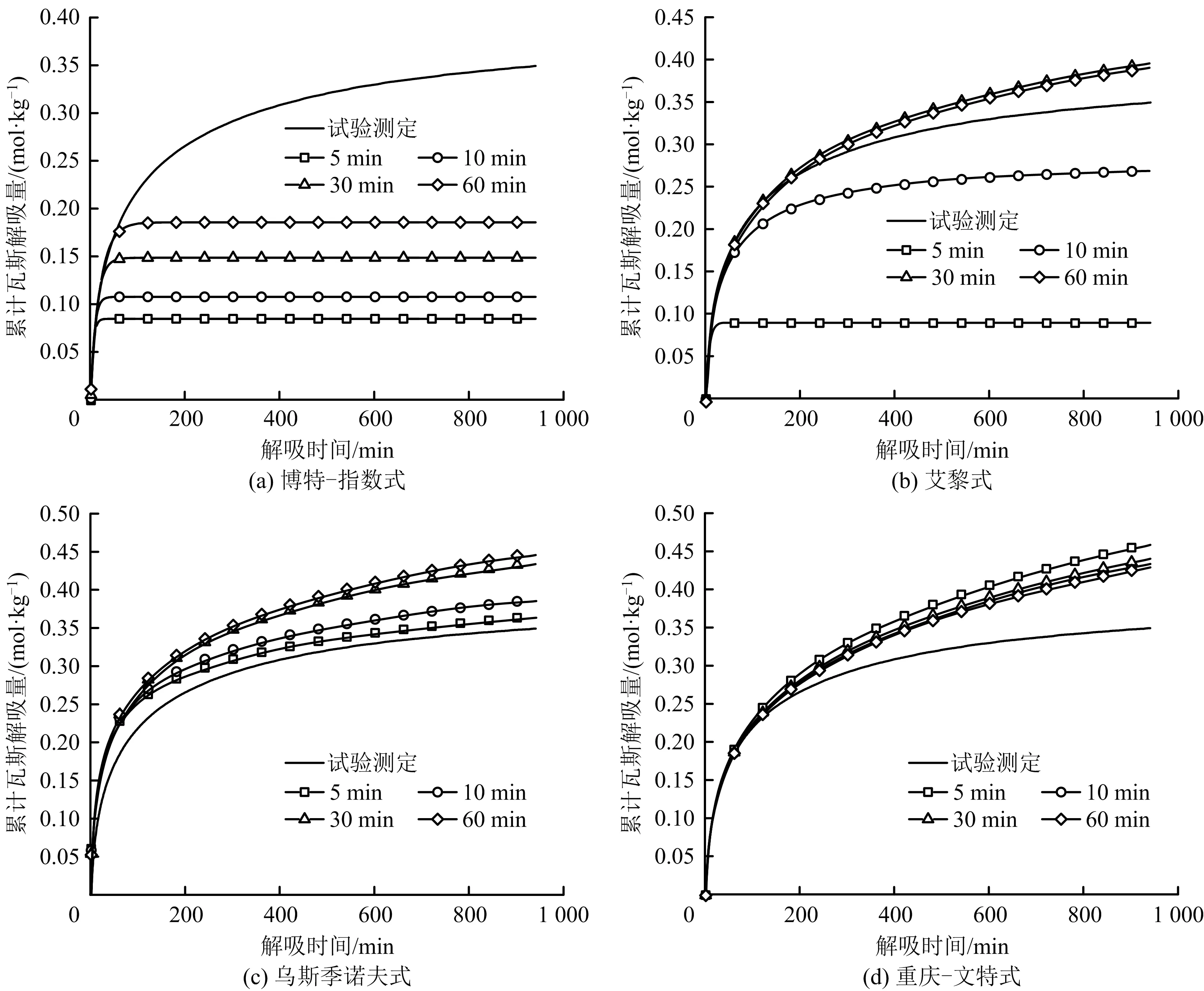
圖5 不同經驗模型公式瓦斯解吸預測量隨時間段的變化Fig.5 Variation of gas desorption prediction amount with time periods by different empirical model formulas

4 結論

1)各個經驗模型公式在擬合不同時間段的煤屑瓦斯累計解吸量時，確定系數R-Square都接近1，表現出較高擬合效果，其擬合效果好劣程度依次為：巴雷爾式<博特-指數式<撫順式<模擬近似式<重慶-文特式<烏斯季諾夫式<艾黎式。

2)巴雷爾式不適合用于煤屑的瓦斯解吸量預測，指數型經驗模型公式計算得到瓦斯解吸量曲線在擬合時間段后很快趨于平直，但會隨著時間段的增長而接近實際測定曲線，其受制于擬合數據時間段長短而低估累計瓦斯解吸量。

3)短時長煤屑瓦斯解吸數據推算預測長期瓦斯解吸量時適合采用烏斯季諾夫式，而預測短期時適合采用重慶-文特式；利用較長時間段瓦斯解吸量數據推算煤屑瓦斯解吸量宜采用艾黎式。