基于二元特征的斷面交通數(shù)據(jù)異常檢測(cè)與修正*
康晉滔,成 衛(wèi),張 靈
(1.昆明理工大學(xué) 交通工程學(xué)院,云南 昆明 650504; 2.昆明市公安局交警支隊(duì)科信處,云南 昆明 650000)
0 引言
隨著智能交通系統(tǒng)(Intelligent Transportation Systems,ITS)的引入和普及,交管部門(mén)已有龐大的交通原始數(shù)據(jù)積累。這些交通數(shù)據(jù)在交通控制、交通規(guī)劃等領(lǐng)域蘊(yùn)含了極大的潛在價(jià)值[1]。然而,受環(huán)境因素、設(shè)備故障等影響,這些數(shù)據(jù)的準(zhǔn)確性仍有待提高。研究表明,交通數(shù)據(jù)庫(kù)里的數(shù)據(jù)準(zhǔn)確率平均值低于70%[2]。因此,為保障智能交通系統(tǒng)有效工作,對(duì)其原始數(shù)據(jù)的異常檢測(cè)與修正尤為必要。
20世紀(jì)90年代,Jacobson等[3]學(xué)者通過(guò)建立交通數(shù)據(jù)最值模型,得到經(jīng)典3參數(shù)的閾值基準(zhǔn),從而對(duì)異常值進(jìn)行檢測(cè);Zhong等[4-5]在此基礎(chǔ)上,采用了插值、回歸等方法,對(duì)數(shù)據(jù)進(jìn)行修正;Min等[6]基于交通數(shù)據(jù)的時(shí)空相關(guān)性,利用鄰接數(shù)據(jù)、歷史數(shù)據(jù)等對(duì)原始數(shù)據(jù)進(jìn)行修正。國(guó)內(nèi)對(duì)于此類(lèi)問(wèn)題的研究起步較晚,大約在2005年后,姜桂艷等[7-9]針對(duì)實(shí)時(shí)動(dòng)態(tài)的交通數(shù)據(jù)提出了異常評(píng)價(jià)體系;徐程等[10]根據(jù)前人的研究成果,建立了一套標(biāo)準(zhǔn)的數(shù)據(jù)預(yù)處理流程。但是這些方法,在大數(shù)據(jù)時(shí)代下,難以高效地處理爆炸式增長(zhǎng)的交通數(shù)據(jù)。
隨著機(jī)器學(xué)習(xí)和深度學(xué)習(xí)的普及,部分學(xué)者也開(kāi)始嘗試訓(xùn)練模型來(lái)處理數(shù)據(jù)。范光鵬等[11]充分挖掘了數(shù)據(jù)在時(shí)間序列上的信息,利用深度學(xué)習(xí)LSTM模型與卡爾曼濾波相結(jié)合,來(lái)預(yù)測(cè)公交車(chē)站到站時(shí)間;Sun等[12]在傳統(tǒng)的KNN算法基礎(chǔ)上,引入時(shí)間窗和權(quán)重,極大拓展了數(shù)據(jù)集規(guī)模,從而在大數(shù)據(jù)框架下建立了GSW-KNN算法;Kim等[13]則是采用優(yōu)化的遞歸神經(jīng)網(wǎng)絡(luò)C-LSTM模型,通過(guò)對(duì)大量歷史交通數(shù)據(jù)的深度挖掘,訓(xùn)練特定場(chǎng)景的數(shù)據(jù)模型,來(lái)檢測(cè)該場(chǎng)景下的交通異常值。
綜上所述,基于交通數(shù)據(jù)時(shí)空相關(guān)性的處理方法,沒(méi)有充分挖掘數(shù)據(jù)本身的邏輯規(guī)律。然而由于道路條件等諸多隨機(jī)因素存在,在實(shí)際工程中交通數(shù)據(jù)的變化往往無(wú)法呈現(xiàn)出既有模型所具有的規(guī)律性,所以基于時(shí)空相關(guān)性的修正方法可能會(huì)出現(xiàn)較大的誤差。常用的交通異常檢測(cè)手段,多基于數(shù)據(jù)的單元特征,分別對(duì)速度或流量等參數(shù)進(jìn)行異常檢測(cè),隨著數(shù)據(jù)多元化的發(fā)展,已經(jīng)無(wú)法滿(mǎn)足智能交通系統(tǒng)的要求。而在數(shù)據(jù)修正過(guò)程中,傳統(tǒng)方法大多根據(jù)交通數(shù)據(jù)的時(shí)空特性,使用大量的歷史數(shù)據(jù),通過(guò)不同的權(quán)重來(lái)對(duì)異常點(diǎn)進(jìn)行相應(yīng)修正。
基于此,提取斷面二元特征向量速度與流量,運(yùn)用多元高斯分布機(jī)器學(xué)習(xí)模型來(lái)進(jìn)行異常數(shù)據(jù)的快速甄別。同時(shí)鑒于灰色馬爾可夫模型[14]在短時(shí)預(yù)測(cè)的領(lǐng)域有著優(yōu)良的擬合效果,提出了1種基于GM(1,1)-Markov模型的異常值修正方法,在此基礎(chǔ)上引入了小時(shí)修正窗口和波動(dòng)性數(shù)據(jù)處理,從便捷性和準(zhǔn)確性2方面優(yōu)化了該組合模型。
1 基于多元高斯分布的異常檢測(cè)
1.1 原始數(shù)據(jù)集二元特征向量提取
交通原始數(shù)據(jù)呈現(xiàn)多源異構(gòu)特征,為了便于后續(xù)的運(yùn)算處理,首先要對(duì)原始數(shù)據(jù)集進(jìn)行標(biāo)準(zhǔn)化處理。本文以10 min為基本單元進(jìn)行標(biāo)準(zhǔn)化,則每天的速度數(shù)據(jù)和流量速度分別有144組,即V=v1,v2,v3,,v144,Q=q1,q2,q3,,q144。原始數(shù)據(jù)集最終可表示為Xt=(V,Q),式中t為該數(shù)據(jù)集的日期,即t=1,2,3,,31。取第1天交通數(shù)據(jù)X1為訓(xùn)練集,并對(duì)X1進(jìn)行異常標(biāo)定,用于多元高斯異常檢測(cè)模型的訓(xùn)練。
1.2 基于速度和流量的二元高斯異常檢測(cè)
實(shí)際工程中,即使數(shù)據(jù)分布不太符合高斯分布,可以通過(guò)函數(shù)變換使其滿(mǎn)足高斯分布,這一過(guò)程稱(chēng)為高斯化。大量的實(shí)驗(yàn)[15]表明,原數(shù)據(jù)不進(jìn)行高斯化處理,異常檢測(cè)算法也能夠良好運(yùn)行。因此,本文認(rèn)為流量、平均速度等數(shù)據(jù)服從高斯分布。
根據(jù)交通工程學(xué)大量的研究,交通流三參數(shù)數(shù)據(jù)為相關(guān)性較高[16]的隨機(jī)變量。如果使用普通高斯算法,則無(wú)法表征特征向量之間的關(guān)聯(lián)性;多元高斯分布模型則可以自動(dòng)捕獲特征之間的相關(guān)。本文提取速度和流量二元特征,而每日的樣本數(shù)量144遠(yuǎn)大于特征數(shù)量2,因此滿(mǎn)足使用多元高斯異常檢測(cè)算法的前提條件。
對(duì)于訓(xùn)練集二元隨機(jī)變量X1=(V,Q),具備如下的概率分布密度函數(shù):
(1)
式中:n為特征向量(速度和流量)的數(shù)量,取2;μ為對(duì)應(yīng)特征向量的均值;Σ為二元特征數(shù)據(jù)集的協(xié)方差矩陣。
根據(jù)多元高斯模型的公式,使用matlab編程計(jì)算出X1=(V,Q)的參數(shù)μ和Σ,從而擬合出模型p(x)以及閾值參數(shù)ε。然后,將測(cè)試數(shù)據(jù)集輸入該模型p(x),計(jì)算出對(duì)應(yīng)點(diǎn)p(x)的值。通過(guò)比較計(jì)算出p(x)值與模型異常閾值ε,當(dāng)p(x)<ε時(shí),判斷對(duì)應(yīng)的數(shù)據(jù)點(diǎn)為異常值,否則為正常值。
2 基于GM(1,1)-Markov的數(shù)據(jù)修正
2.1 小時(shí)修正窗口的引入
通過(guò)異常檢測(cè)算法,可得到原始數(shù)據(jù)集中的異常點(diǎn)。假設(shè)存在異常點(diǎn)xi,xj,xk,,其中i,j,k,分別表示上節(jié)檢測(cè)出的異常點(diǎn)在原始數(shù)據(jù)集中的角標(biāo)編號(hào)。
針對(duì)每1個(gè)異常數(shù)據(jù)點(diǎn),分別建立小時(shí)修正窗口,即每個(gè)窗口(含異常點(diǎn))有6個(gè)數(shù)據(jù)。根據(jù)GM(1,1)模型的特點(diǎn),第1個(gè)數(shù)據(jù)點(diǎn)為基準(zhǔn)點(diǎn),不會(huì)被擬合計(jì)算。因此每個(gè)異常點(diǎn)有5種不同的修正窗口。用W分別表示這些窗口為:W=[xi-5,xi-4,xi-3,xi-2,xi-1,xi],[xi-4,xi-3,xi-2,xi-1,xi,xi+1],[xi-3,xi-2,xi-1,xi,xi+1,xi+2],[xi-2,xi-1,xi,xi+1,xi+2,xi+3],[xi-1,xi,xi+1,xi+2,xi+3,xi+4]。
經(jīng)過(guò)大量的實(shí)驗(yàn)運(yùn)算,得出選取將異常點(diǎn)作為窗口最后1個(gè)數(shù)據(jù)的修正窗口得到的修正值為最優(yōu)。若首次修正效果不滿(mǎn)足異常檢測(cè),則依次選取其他形式的修正窗口進(jìn)行異常點(diǎn)再修正。
2.2 修正窗口數(shù)據(jù)集波動(dòng)性處理
當(dāng)數(shù)據(jù)出現(xiàn)波動(dòng)性變化時(shí),GM(1,1)模型的擬合效果會(huì)受到影響,因此采取1種補(bǔ)加增量的方法,弱化原始數(shù)據(jù)的隨機(jī)性,提高灰色模型的運(yùn)算精度。

(2)
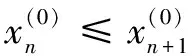
(3)
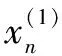
2.3 GM(1,1)-Markov模型
通過(guò)GM(1,1)灰色模型的擬合,找出數(shù)據(jù)的外在變化趨勢(shì);進(jìn)一步利用馬爾可夫模型,挖掘時(shí)序數(shù)據(jù)內(nèi)在狀態(tài)的轉(zhuǎn)移規(guī)律。具體步驟如下:
1)對(duì)數(shù)據(jù)集X(1)進(jìn)行1次累加處理:
(4)
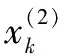
2)定義鄰值生成數(shù):
(5)
式中:zk為X(2)的鄰值生成數(shù)列。
3)建立GM(1,1)模型:
(6)
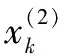
(7)
式中:α為發(fā)展系數(shù),β為灰作用量。用回歸分析求α,β的值。可得:
(8)
(9)
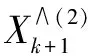
4)還原原始數(shù)據(jù)修正值:
(10)
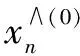
5)求出窗口修正數(shù)據(jù)集的相對(duì)殘差:
(11)
式中:k=1,2,,n。
6)劃分狀態(tài)區(qū)間:根據(jù)相對(duì)殘差范圍集中程度進(jìn)行劃分。假設(shè)劃分好的區(qū)間為E1,E2,Ej,j為區(qū)間的個(gè)數(shù)。
7)確定狀態(tài)轉(zhuǎn)移矩陣:
(12)
式中:Pab為狀態(tài)Ea轉(zhuǎn)移到狀態(tài)Eb(b>a)的轉(zhuǎn)移概率;mab表示由Ea一步轉(zhuǎn)移到Eb出現(xiàn)的次數(shù),Ma表示狀態(tài)Ea出現(xiàn)的總次數(shù)。確立1步狀態(tài)轉(zhuǎn)移矩陣:
(13)
Pk=v0·P
(14)

(15)
式中:λ+η=1,本文使用平均權(quán)值。
2.4 斷面交通異常數(shù)據(jù)質(zhì)量控制
對(duì)于斷面交通異常數(shù)據(jù),運(yùn)用上述算法,建立整套質(zhì)量控制流程如圖1所示。算法總體分為2大部分,即異常檢測(cè)與數(shù)據(jù)修正。
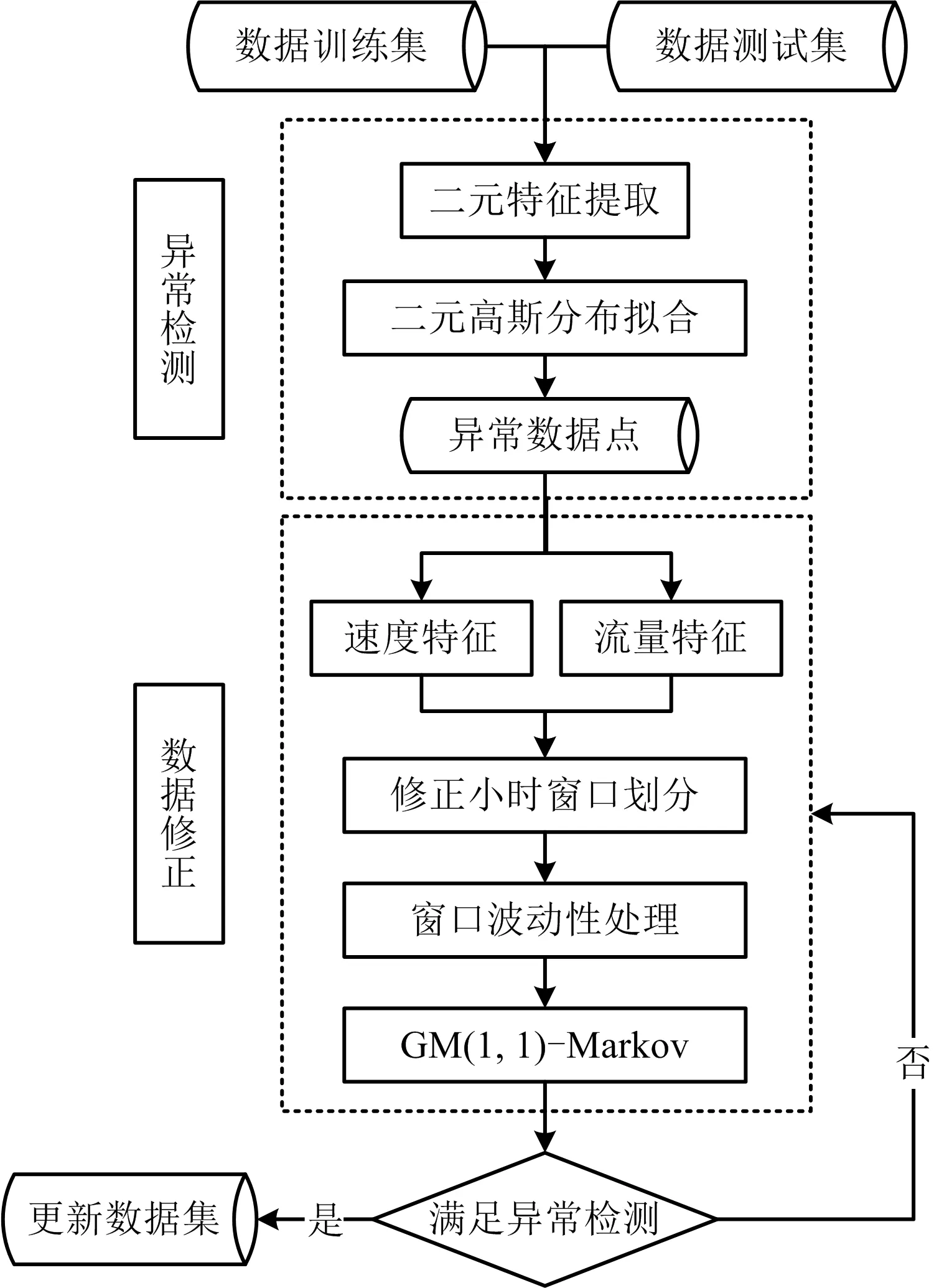
圖1 交通異常數(shù)據(jù)質(zhì)量控制流程Fig.1 Quality control procedure of traffic abnormal data
3 樣本實(shí)驗(yàn)
選取汕昆高速K2077斷面數(shù)據(jù),樣本數(shù)據(jù)集為2018年5月該斷面的交通流量以及速度數(shù)據(jù)。首先,對(duì)原始數(shù)據(jù)進(jìn)行標(biāo)準(zhǔn)化處理及二元特征提取,5月1日部分標(biāo)準(zhǔn)化數(shù)據(jù)如表1所示。

表1 樣本部分標(biāo)準(zhǔn)化數(shù)據(jù)Table 1 Partial standardized data of sample
為了便于二元高斯模型的訓(xùn)練,將所有流量數(shù)據(jù)乘以0.5,做歸一化處理。
3.1 異常檢測(cè)
使用5月1日數(shù)據(jù)集作為二元高斯模型訓(xùn)練集,5月2日數(shù)據(jù)集作為驗(yàn)證集。模型訓(xùn)練后得出異常檢測(cè)閾值ε=1.735 759e-04。檢測(cè)出驗(yàn)證集中異常數(shù)據(jù)角標(biāo)編號(hào)分別為9,24,40,49,126,128,139共計(jì)7個(gè)異常數(shù)據(jù)點(diǎn)。二元高斯模型異常檢測(cè)程序在matlab中運(yùn)行結(jié)果如圖2所示。
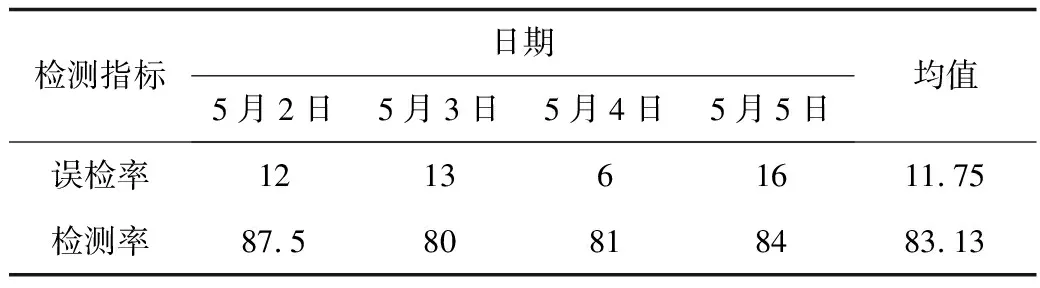
為驗(yàn)證此異常檢測(cè)算法的有效性,繼續(xù)使用5月3日、5月4日、5月5日數(shù)據(jù)作為測(cè)試集。分別檢測(cè)出對(duì)應(yīng)數(shù)據(jù)集異常值,并計(jì)算出對(duì)應(yīng)的誤檢率和檢測(cè)率,如表2所示。
通過(guò)對(duì)上述4天交通數(shù)據(jù)進(jìn)行二元高斯分布異常檢測(cè),其結(jié)果表明:模型異常檢測(cè)率均值可達(dá)83.13%,而其中誤檢率均值僅為11.75%。
3.2 數(shù)據(jù)修正
對(duì)5月2日數(shù)據(jù)集檢測(cè)出的異常點(diǎn),進(jìn)行修正窗口劃分,將這些異常修正窗口在全天數(shù)據(jù)集中標(biāo)記出來(lái),如圖3所示。每一個(gè)窗口具有6個(gè)數(shù)據(jù),異常數(shù)據(jù)點(diǎn)置于末端。

圖2 異常檢測(cè)模型可視化結(jié)果Fig.2 Visualization results of anomaly detection model
檢測(cè)指標(biāo)日期5月2日5月3日5月4日5月5日均值誤檢率121361611.75檢測(cè)率87.580818483.13
波動(dòng)性處理前后灰色(1,1)模型擬合平均相對(duì)誤差對(duì)比如表3所示,由表3中數(shù)據(jù)可知,直接使用灰色模型對(duì)窗口數(shù)據(jù)進(jìn)行處理,則各修正窗口擬合平均相對(duì)誤差的均值在20%以上。經(jīng)過(guò)波動(dòng)性處理優(yōu)化之后,灰色模型各窗口平均相對(duì)誤差的均值不足10%。
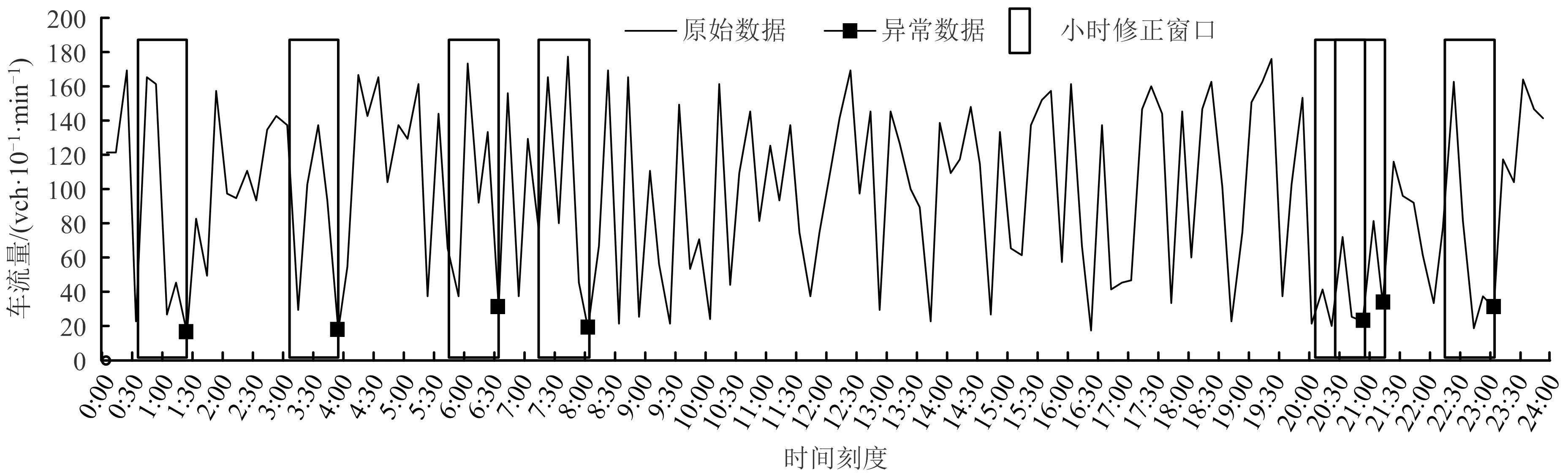
圖3 劃分修正窗口Fig.3 Partition of correction windows

模型窗口窗口1窗口2窗口3窗口4窗口5窗口6窗口7均值GM(1,1)21.0716.1845.339.9315.6925.6322.5322.34優(yōu)化GM(1,1)3.686.8129.055.8110.152.709.779.71
各個(gè)窗口的修正過(guò)程如圖4所示。由于最終的修正數(shù)據(jù)集更新只針對(duì)異常點(diǎn),因此窗口的其他點(diǎn)只參與狀態(tài)轉(zhuǎn)移的概率劃分,而不計(jì)算其最終的馬爾可夫調(diào)整量。
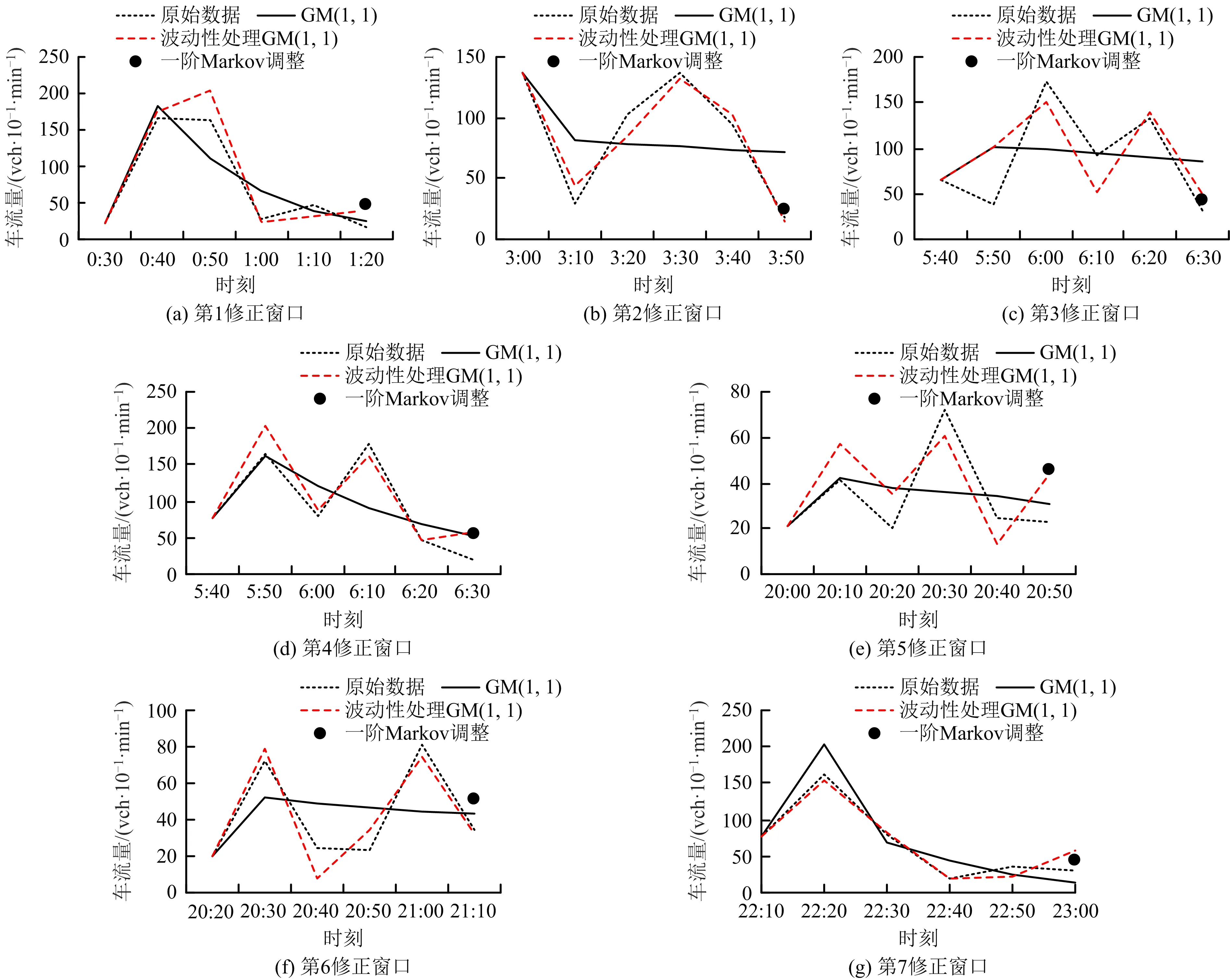
圖4 各窗口模型修正Fig.4 Model correction of each window
3.3 結(jié)果論證
為了驗(yàn)證本文提出的優(yōu)化GM(1,1)-Markov修正方法的有效性,選取歷史數(shù)據(jù)修正和移動(dòng)平均修正2種方法作為對(duì)比論證。每種方法修正的數(shù)據(jù)分別與對(duì)應(yīng)窗口的數(shù)據(jù)集平均值做絕對(duì)誤差(Absolute Error)、相對(duì)誤差(Relative Error)、以及均方根誤差(Root Mean Squared Error)計(jì)算。3種方法對(duì)異常點(diǎn)的修正誤差分析如表4所示。
通過(guò)上述3種交通數(shù)據(jù)修正方法的誤差分析,得出波動(dòng)性?xún)?yōu)化GM(1,1)-Markov深入挖掘了原始數(shù)據(jù)集的內(nèi)在規(guī)律,算法誤差小且具備很強(qiáng)的魯棒性。在不使用大量歷史數(shù)據(jù)的前提下,能夠起到良好的修正效果。
4 結(jié)論
1)以斷面數(shù)據(jù)的時(shí)間刻度為標(biāo)簽,提取該標(biāo)簽數(shù)據(jù)的二元特征向量,即速度和流量,運(yùn)用二元高斯分布擬合的模型,快速準(zhǔn)確地檢測(cè)出異常數(shù)據(jù)。今后還可以推廣到多元特征向量,例如涵蓋交通檢測(cè)器常有的占有率數(shù)據(jù)集。
2)對(duì)異常數(shù)據(jù)進(jìn)行針對(duì)性修正,引入小時(shí)窗口既使得修正過(guò)程清晰便捷又避免大量冗余數(shù)據(jù)的復(fù)合運(yùn)算。采用GM(1,1)-Markov則可以在小時(shí)窗口內(nèi)部較好地表征出異常點(diǎn)的客觀規(guī)律變化,從而進(jìn)行修正。
3)鑒于短時(shí)交通數(shù)據(jù)的隨機(jī)波動(dòng)性大,引入波動(dòng)性?xún)?yōu)化處理彌補(bǔ)了GM(1,1)-Markov模型局部失真的缺陷。

表4 修正數(shù)據(jù)誤差對(duì)比Table 4 Error comparison of corrected data
 中國(guó)安全生產(chǎn)科學(xué)技術(shù)2019年9期
中國(guó)安全生產(chǎn)科學(xué)技術(shù)2019年9期
- 中國(guó)安全生產(chǎn)科學(xué)技術(shù)的其它文章
- 水化煤飽和-風(fēng)干過(guò)程的自燃特性實(shí)驗(yàn)研究*
- 潞安礦區(qū)煤層滲透率的各向異性特征實(shí)驗(yàn)研究*
- 可燃制冷劑空調(diào)用開(kāi)關(guān)元件點(diǎn)燃危險(xiǎn)及防爆試驗(yàn)分析*
- 情景構(gòu)建理論沿革及其對(duì)我國(guó)應(yīng)急管理工作的啟示*
- 常用經(jīng)驗(yàn)?zāi)P皖A(yù)測(cè)煤屑瓦斯解吸量對(duì)比分析*
- 基于模糊Petri網(wǎng)的城市突發(fā)性燃?xì)舛倘睉?yīng)急能力評(píng)估*
