基于混行策略的橋式起重機主梁輕量化設計

陸鳳儀,任 重,徐格寧,董 青,徐 彤

(1.太原科技大學 機械工程學院,山西 太原 030024; 2.上海云童機械有限公司,上海 200126)

在結構優化設計中,通常將某一要求(如截面最小、質量最輕等)作為目標,使其在給定的約束條件下得到最優結果,如起重機一般將自重作為優化目標,通過優化截面尺寸實現減重目的.實現方法包括:準則法、數學歸納法、混合法等,傳統方法伴隨著設計周期長、結果偏大的問題,因此，現多采用啟發式算法實現.

文獻[1]利用改進人工蜂群算法對16 t/10.5～22.5 m橋式起重機主梁截面進行優化,提出了基于差分進化算法(Differential Evolution Algorithm，DE)的人工魚群算法(Artificial Fish Swarm Algorithm，AFSA),并引入遺傳算法(Genetic Algorithm，GA)中的交叉、變異算子提高其全局收斂性.文獻[2]利用改進微粒群算法(Particle Swarm Optimization,PSO)對32 t/25.5 m橋式起重機主梁進行優化,通過改進慣性權重、加速因子值使算法具有較好的全局、局部搜索能力.

雖然針對單一優化算法中存在早熟現象明顯、收斂速度慢、尋優精度不足、對初始種群敏感等缺陷[3]提出過各種改進,但無法面面俱到,為此誕生了混合、并行算法.Hua等[4]提出一種結合GA和Levenberg-Marquardt(LM)的混合算法,充分利用了GA和LM的優點,分別抑制它們局部收斂不足、全局搜索能力差的特點,如圖1(a)所示,其結果受GA生成的初始解影響,穩定性較差.Tang等[5]提出一種結合GA和模擬退火算法(Simulated Annealing Algorithm，SAA)的混合算法,將SAA嵌入GA交叉算子中,揚長避短,但兩者均為基于概率機制的算法,如圖1(b)所示,因此，穩定性方面較差.Farnad等[6]提出結合GA,PSO和共生生物搜索算法(Symbiotic Organisms Search,SOS)的混合算法,該算法分3個階段:GA擴大種群數量并將最好種群傳遞給下一階段,PSO通過自主學習使種群得到進化而后傳遞下一階段,SOS通過優勝劣汰選擇最優結果,如圖1(c)所示，由于初始算法為GA,使得該算法具有一定的概率性.Tsoulos等[7]提出并行遺傳算法,將一組工作劃分成兩小組,同時進行運算,如圖1(d)所示.Orhan[8]開發了一種基于交叉和變異機制的混合蟻群算法,將遺傳算法引入蟻群算法,解決了易陷入局部最優問題.

上述改進均將GA作為起始算法,初始解直接決定最后結果的精度,使得優化結果具有一定的概率性.因此，本文提出一種混行算法,如圖1(e)所示,最大限度降低不確定結果出現的概率.

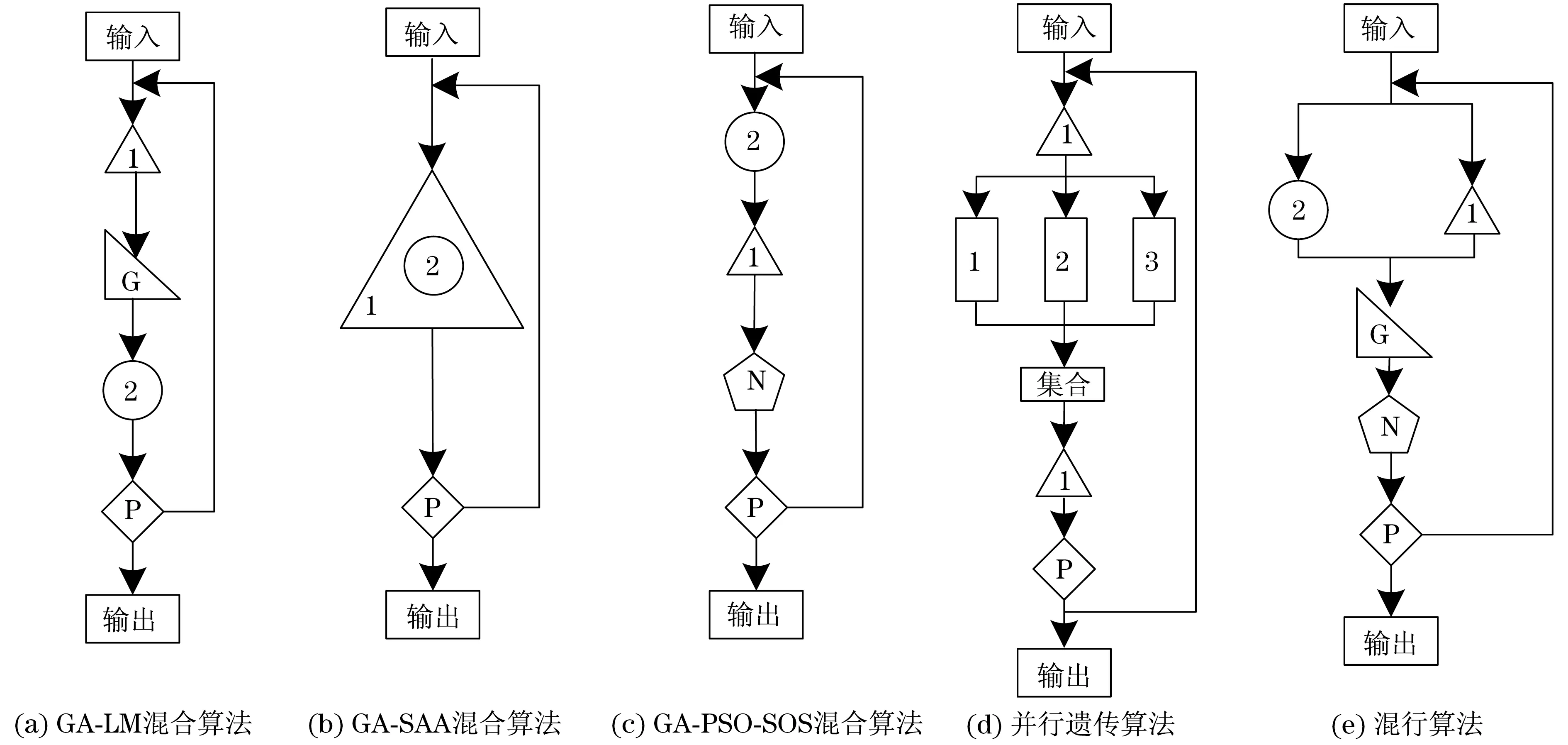
圖1 國內外混合、并行算法框圖Fig.1 Diagram of hybrid and parallel algorithm running at home and abroad

2 混行算法

以“揚長避短”為理念,本文提出混行算法的概念.區別于混合、串行算法,混行是將串行與并行按照一定規則相結合,運算過程中分別利用串行、并行算法優勢,達到“快、準、穩”的求解目標.

2.1 GA & AFSA

2.1.1GA

GA是一種模擬自然選擇和生物進化的啟發式算法,其中交叉算子提供全局搜索能力,變異算子提供局部搜索能力[9].為避免陷入局部最優,本文分別對交叉算子進行改進.

傳統交叉算子采用隨機選擇父代染色體中幾個基因起始位置(兩染色體被選擇位置、數量相同),然后交換兩者位置,交叉即完成.這種交叉方式存在一定問題:簡單隨機重組可減緩搜索速度、出現局部收斂或早熟收斂等[10],所以設計了如圖2所示的改進方法.父代染色體中隨機生成發生交叉的基因個數(位置不連續),交換時采用隨機生成的交叉順序,可提高其全局收斂性.Matlab交叉算子改進部分程序如圖3所示.

2.1.2AFSA

AFSA是一種通過人工魚來模擬魚群的覓食、聚群、追尾行為,達到尋優目標的啟發式算法[11-12].以下為其幾種典型行為:

(1) 覓食行為(AF_prey).數學表達式為

Xi/next=Xi+Random(Step),Yi≤Yj

(1)

式中:Yj為狀態Xj對應的食物濃度;Xi為第i條人工魚的狀態;Random(Step)為[0,Step]間的隨機數;di,j=‖Xj-Xi‖為人工魚個體之間的距離.

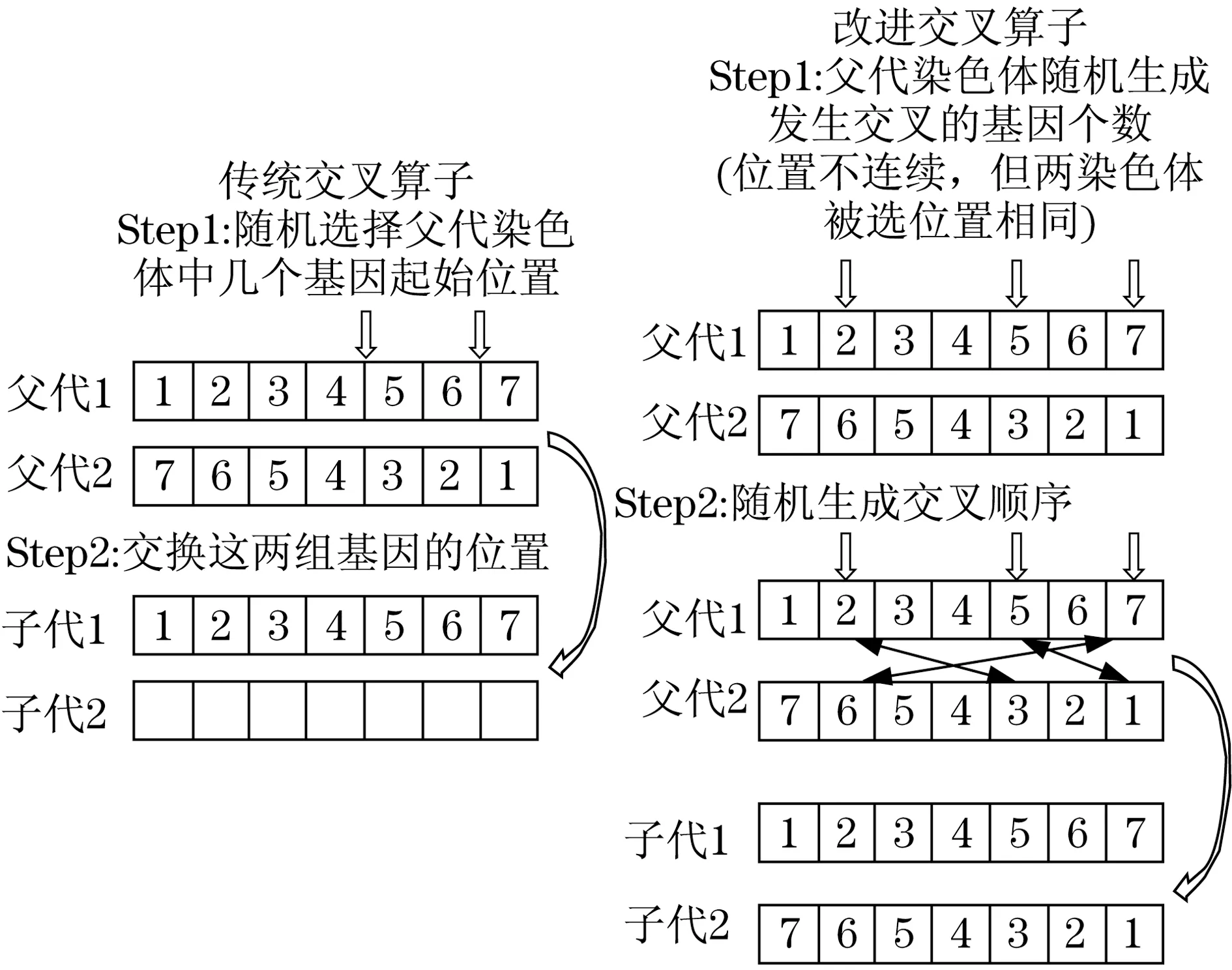
圖2 交叉算子改進示意圖Fig.2 Improved schematic diagram of crossover operator

圖3 交叉算子改進程序Fig.3 Crossover operator improvement program

(2) 聚群行為(AF_swarm).設人工魚當前狀態為Xi，搜索其臨域內(即di,j≤Visual)的伙伴數目nf和中心位置Xc，若對應的食物濃度Yc/nf>δYi(伙伴中心具有較多食物，且不太擁擠)，則向伙伴中心Xc移動一步，否則執行覓食行為.其數學表達式為

(2)

(3) 追尾行為(AF_follow).設當前人工魚狀態為Xi，搜索其臨域內(即di,j≤Visual)伙伴中Yi為最大的Xi，且滿足Yc/nf>δYi(伙伴Xi具有較多食物，且不太擁擠)，Xi臨域內伙伴數目為nf,則朝伙伴Xi前進一步，否則執行覓食行為.其數學表達式為

(3)

(4) 隨機行為(AF_random).人工魚在視野范圍內隨機選擇一個狀態,然后向其移動,以便更大范圍內尋覓食物或伙伴,該行為為覓食行為的缺省行為.

魚群通過側向反饋機制覓食,這導致其易陷入局部最優,因此,提出增加干擾行為,增加跳出局部最優解的概率.DE[13]中的變異算子可以擴大魚群間差異性,且隨機性小、可控性強,所以在覓食、聚群、追尾后增設干擾行為,其數學形式為[14]

(4)

式中:F為縮放因子;Xr1為基向量;Xr2,Xr3為差向量.

2.2 混行算法

混行算法流程圖如圖4所示,執行步驟如下.

步驟1確定變量個數,輸入對應變量范圍.

步驟2執行并行算法模塊:① AFSA部分,計算每條人工魚適應度值,執行聚群、追尾(覓食、隨機行為伴隨聚群、追尾發生)行為,分別生成新個體,計算新個體適應度值,判斷兩者大小,選擇較小個體替換原種群中對應的個體;② 判斷新個體是滿足變量條件,如不滿足則取對應變量的上下限取代原有值;③ 對新生成的個體實施干擾行為,擴大魚群間差異性;④ 判斷是否滿足迭代要求,如不滿足則繼續執行步驟①,如滿足則跳出循環,輸出運行結果1;⑤ GA部分,計算單個染色體適應度值,執行交叉、變異行為,待所有個體循環結束后,記錄當代中最優個體,替換最差個體;⑥ 判斷新染色體是否滿足變量條件,如不滿足則取對應變量的上下限取代原有值;⑦ 判斷是否滿足迭代要求,如不滿足則繼續執行步驟⑤,如滿足則跳出循環,輸出運行結果2.

步驟3對比運行結果1和2,保留優勝值.

步驟4根據橋式起重機板厚選擇原則重新設定變量范圍,設置對應的步長.

步驟5將根據新范圍生成的數值矩陣代入解析法中,驗證滿足約束條件的解.

步驟6校核二次優化后生成的解,分別判斷其是否滿足要求,保留符合要求的結果.

步驟7輸出優化結果,混行算法結束.

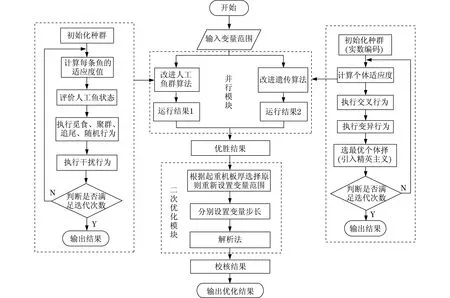
圖4 混行算法流程圖Fig.4 Flowchart of a mixed-line algorithm

3 構建數學優化模型

為實現起重機結構的輕量化設計,如圖5所示，q為主梁自重均布載荷，F1，F2為輪壓，s為跨度.現多采用優化算法來實現尺寸優化,從而達到起重機減重目的[15].尺寸優化主要通過主梁截面面積來表達,數學表達式為

(5)

式中:Ai為不同結構截面面積.

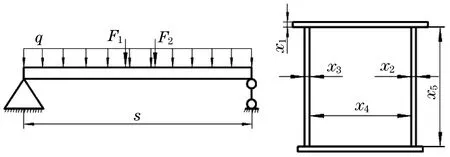
圖5 主梁力學模型簡圖Fig.5 Schematic diagram of mechanical model of main girder

當小車位于跨中時,主梁承受最大彎矩,跨中截面各驗算點的彎曲正應力和切應力為

σ0x=Mx/Wx

(6)

式中：Mx計算截面對強軸(x軸)的彎矩；Wx為計算截面對強軸(x軸)的抗彎截面系數；F為梁的剪切力；S為梁在最大剪切力截面的毛截面最大靜矩；Ix為梁在最大剪切力截面的毛截面慣性矩；δ為梁腹板厚度.

強度約束條件為

(7)

式中:M為危險截面承受的彎矩;y為截面中性軸到驗算點的垂直距離;[σ]為許用應力,[σ]=235/1.48=158.78 MPa.

剛度約束條件為

(8)

式中:Yc為集中載荷位于跨中時主梁最大變形;[Y]為許用靜位移,[Y]=L/500.

幾何約束條件為

(9)

式中:x1為上、下翼緣板厚度;x2為主腹板厚度;x3為副腹板厚度;x4為主副腹板間距;x5為腹板高度.

4 工程應用

為驗證混行算法的實用性,以32 t/22.5 m橋式起重機主梁截面作為優化工程實例.考慮結果的對比性,載荷參數采用文獻[2]中數據,如表1所示.

表1 橋式起重機參數Tab.1 Parameters of bridge crane

并行模塊運行結束后,需根據求解結果重新設定變量范圍與對應步長,設置如下:

(10)

通常梁的上、下翼緣板采用相同厚度,腹板厚度為6～14 mm,兩者均取2的整倍數.因此,設置上、下翼緣板厚度取值步長為2 mm[16],主副腹板(翼緣板寬度)間距及腹板高度的取值步長x4,x5為10 mm,如表2所示.

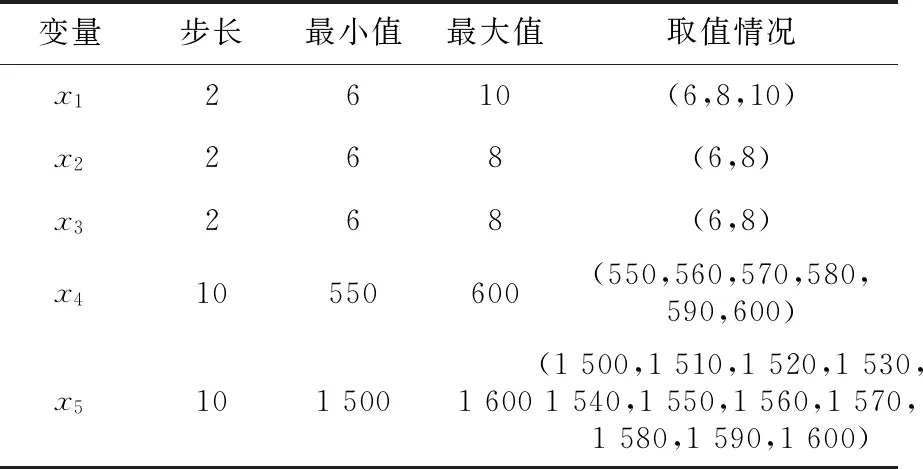
表2 二次優化參數設置Tab.2 Two-time optimization parameter settings mm

按照排列組合的方式將所有結果排列,采用解析法對其進行校核,從中選出最優組合作為二次優化的結果(見表3).

混行算法在Matlab中運行,參數采用表1中數據，運行結果如表4所示.

表3 x1選取6 mm時排列組合結果Tab.3 x1 selection of 6 mm time combination results

注:表中x5代表1 500,1 510,1 520,1 530,1 540,1 550,1 560,1 570,1 580,1 590,1 600.

表4 箱型梁優化結果Tab.4 Optimization results of box girder

通過工程驗證,結果滿足強度、剛度以及幾何約束條件.證明混行算法可以應用于橋式起重機主梁尺寸優化設計.

5 結論

針對單一優化算法中存在早熟現象明顯、對初始種群敏感等缺陷,本文提出一種全新的混行算法運用于橋式起重機主梁輕量化設計.混行算法以“揚長避短”為設計理念,分別運用不同算法優勢,取長補短從而達到“快、準、穩”的求解目標.結果表明：在32 t/22.5 m橋式起重機主梁截面優化過程中采用混行算法是合理的,對截面優化任務的最小化是成功的.