遺傳算法優化的運動冗余3-PRRR平面并聯機械手控制研究

鄧小芳,高 銳,孫貴生

(1.貴州省電子信息技師學院 機械制造工程系,貴州 都勻 558000; 2.重慶理工大學 機械工程學院,重慶 401135)

隨著工業技術的發展,并聯機械手被廣泛應用于醫療、工程和航空等各個領域[1-2].并聯機械手的冗余一般分為運動冗余和驅動冗余.當機械手的移動性大于所需的自由度時(Degree of Freedom,DOF),即為運動冗余.反之,當機械手中的執行器數目大于移動性時,即為驅動冗余[3].然而,大多數的研究[4-5]都對驅動冗余進行了討論,在不增加移動性的情況下,機械手控制的執行器多于所需的執行器.近年來,一些關于運動學冗余的研究已經展開[6-7],這類冗余既可以提高機械手的靈活性,又可以擴大機器人的工作空間.此外,通過有效地增加工作空間中的無奇異區域,運動冗余并聯機器人被廣泛應用于提高軌跡跟蹤性能.Wang等[8-9]研究了3種新型運動冗余并聯機器人的奇異性,結果表明,與非冗余度機械手相比,無奇異結構得到了明顯的改善.Cha等[10-11]提出了一種避免3-RRR機構奇異性的運動冗余分解算法,并確定了給定軌跡處于無奇異區的運動冗余主動移動關節變量的允許范圍.大部分研究工作集中在運動學設計、工作空間和奇異性避免等方面,很少有作者研究運動冗余平面并聯機器人的受力能力.文獻[12-13]提出了一種在不考慮機械手路徑情況下,確定3-RPRR機械手受力能力的優化方法,并與非冗余并聯機器人相比,取得了更好的效果.對此,為進一步提高3-RPRR機械手的精確控制,減少末端執行器的致動力矩,本文對3自由度運動冗余3-PRRR平面并聯機械手進行了運動學分析,基于雅可比矩陣方法確定了各關節力矩的數學模型,為避免運動過程中出現奇點,采用二進制編碼遺傳算法對直線運動軌跡的機械手進行了致動力矩優化.在Matlab/Simulink環境下對非冗余3-RRR機械手、1-DOKR、2-DOKR、3-DOKR冗余機械手進行仿真和對比分析.仿真結果表明,采用冗余3-PRRR可有效避免奇點處的致動力矩無限大問題,不同自由度下可進一步減小致動力矩的大小,實現并聯機械手的平滑軌跡跟蹤.

1 3-PRRR并聯機構

本文所研究的3自由度運動冗余3-PRRR平面并聯機械手可簡化為如圖1所示的機械手構形.該機構由3條支鏈構成,每條支鏈均由3個轉動副(R)和1個移動副(P)組成,與基座固連的為驅動轉動副,與動平臺(末端執行器)相連的為被動轉動副.移動副沿著平臺上導軌AiOi(i=1,2,3)運動,3個移動副與水平面的夾角用αi(i=1,2,3)表示;最大允許移動范圍用ρi表示.3個轉動副之間通過驅動連桿l1i(i=1,2,3)和被動連桿l2i(i=1,2,3)相連,長度均為l,兩連桿之間的角度用βi(i=1,2,3)表示,驅動連桿與移動副之間的角度表示為θi(i=1,2,3).

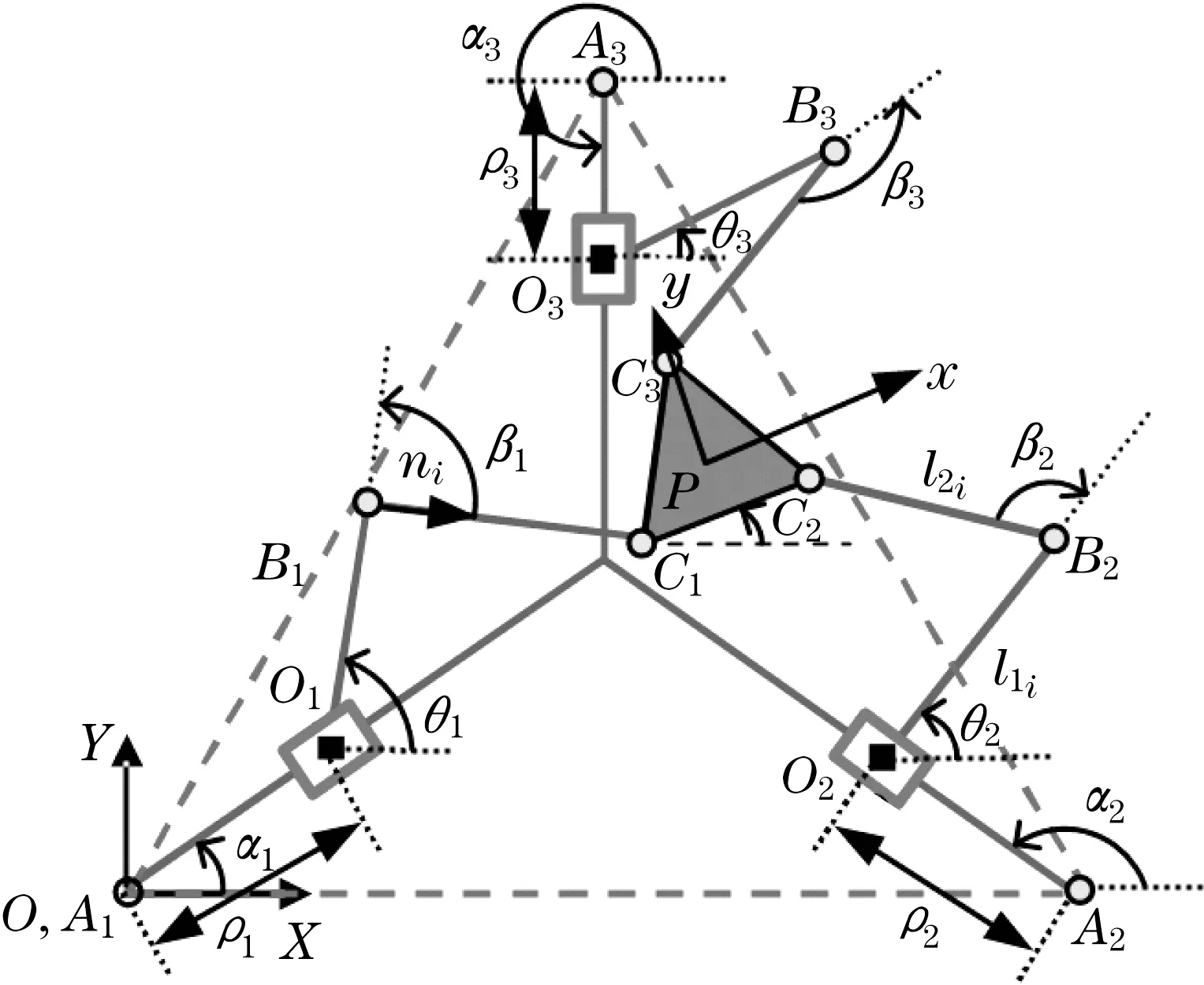
圖1 冗余3-PRRR機械手構形Fig.1 Configuration of redundant 3-PRRR manipulator

如果點Ai與Oi(i=1,2,3)重合,則該構造為非冗余3-RRR機械手.通過在3-RRR機械手的支臂上添加額外的移動副關節,推導出冗余3-PRRR機構的基本結構.增加的移動副關節可以連接到任意的基關節,運動冗余(1-DOKR)可在一定程度上減少3-RRR平面機械手的直接運動奇異點數[5].因此,在每種情況下,3-RRR機械手的每條分鏈都增加了一級運動冗余度,分別為1-DOKR，2-DOKR和3-DOKR.增加的運動冗余使機械手能夠避免運動奇異,提高操縱性,擴大其可達的工作空間和靈巧度,并且減少執行器靠近基座時重量導致的動態效應.

2 并聯機構致動力矩

雅可比矩陣表示了操作空間與關節空間之間速度與力的傳遞關系,是并聯機構性能分析與評價的基礎.在分析冗余3-PRRR機械手構形基礎上,為避免機械手運動過程中出現奇異點,采用雅可比矩陣方法獲得各關節力矩及驅動力矩.

在靜態條件下,在機械手轉動和移動執行機構的速度已知時,關節力/扭矩與末端執行器之間的關系可表示為

(1)

對于式(1)中指定的末端執行器作用力F,其廣義驅動關節力矩/力由下式給出:

(2)

2.1 非冗余3-RRR并聯機構雅可比矩陣

首先對3-RRR非冗余并聯機構進行了雅可比矩陣求解,在此基礎上推導獲得3-PRRR冗余并聯機構的雅可比矩陣.

機械手雅可比矩陣的速度方程基于輸入q=[θ1,θ2,θ3]T(關節位移)和輸出x=[x,y,φ]T(末端執行器姿態)變量隨時間變化的微分非線性閉環方程f(q,x)=0獲得,可表示為

(3)

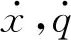
整體雅可比矩陣J可以表示為

(4)

式中:JX，Jq分別為正雅克比矩陣和逆雅克比矩陣.

在反位移[3]的基礎上,考慮圖1所示的非冗余3-RRR平面并聯機械手的幾何結構,通過定義沿遠端連桿的單元矢量ni可獲得閉環方程.因此,每個運動鏈都可以得到以下關系:

(5)

對式(5)的兩邊進行平方并應用余弦定律得

(6)

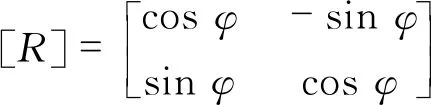
對式(6)求微分,可以獲得以下雅克比矩陣:

(7)

式中:Z為沿z方向的單位向量.

對機械手的3個支柱用矩陣形式表示為

(8)

上述式(8)類似于式(3),表示非冗余3-RRR平面并聯機械手的雅克比矩陣.

2.2 冗余3-PRRR并聯機構雅可比矩陣

基于3-RRR雅可比矩陣,根據圖1可獲得3-PRRR運動冗余并聯機械手的閉環方程，即

對式(8)關于時間求微分,可以得到以下雅可比矩陣:

(11)

運動冗余機構的所有3個支柱可以用矩陣形式表示為

1-DOKR:

(12)

2-DOKR:

(13)

3-DOKR:

(14)

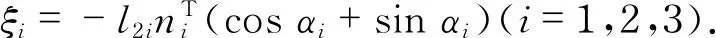
式(12)～式(14)與式(3)類似,表示冗余3-PRRR平面并聯機械手的雅可比矩陣,并對雅可比矩陣進行了維數均質化[11].當運動平臺的速度已知時,所建立的方程允許在非冗余和冗余的情況下，計算轉動和移動執行機構的速度.

3 遺傳算法優化

根據上文得到的關節力矩變化矩陣,從而得到移動關節力矩位置變化.同時,為了能夠確定關節最佳運動位置,使得受可變約束的執行器的力矩最小化,本文采用遺傳算法來實現最佳運動位置的優化.通過采用遺傳算法中二進制編碼字符串,以最小容錯作為終止準則,以最小化關節力矩作為優化目標,獲得最佳的關節運動位置.

最小化關節力矩作為優化的目標,根據第2部分力矩的求解方法,可將其表示為

(15)

關節移動過程中,受到約束主要為機械手各關節連接的連桿之間是否存在軌跡干涉,約束條件可表示為

(16)

式中:ρi,min和ρi,max分別為保證機械手無連桿干涉軌跡的上、下關節極限.

由于關節力矩是關節變量的高度非線性函數,目前,采用二進制編碼遺傳算法來獲得與最小轉矩條件相對應的結構.

采用遺傳算法具體的優化過程總共分為8個步驟:

步驟1對于給定姿態,定義機械手幾何參數;

步驟2定義軌跡;

步驟3從軌跡的初始點開始;

步驟4在邊界內生成冗余移動節點隨機位置;

步驟5計算固定平臺頂點的新坐標;

步驟6用逆運動學計算每點的雅可比行列式;

步驟7在末端執行器上施加扭矩,根據式(14)計算所需的驅動扭矩;

步驟8使用遺傳算法優化程序,使函數f(ρ1,ρ2,ρ3)=τTτ最小化;

步驟9重復步驟4到步驟8的過程,直到軌跡完成.

設定算法的控制參數如下:種群大小為100，進化迭代數為200,遺傳復制方法為輪盤賭法;交叉率為0.8;變異率隨著進化代數的增加從0.1加速增加到0.2.

4 仿真結果分析

為了驗證遺傳算法優化的冗余3-PRRR并聯機械手對關節力矩的優化效果,采用直線軌跡證明優化的有效性,在Matlab/Simulink環境下分別對非冗余3-PRRR并聯機械手和冗余3-PRRR并聯機械手進行了致動力矩仿真研究,并進行了對比分析,同時，分析了1-DOKR,2-DOKR和3-DOKR機械手的致動力矩大小.

4.1 非冗余3-PRRR并聯機械手致動力矩

假設機械手抓取平臺從工作空間中心向工作空間邊緣做直線移動,即從點(280 mm,150 mm)移動到點(480 mm,150 mm),移動步長為1.0 mm.機械手恒定幾何參數為AiAj=500 mm和CiCj=200 mm,l1i=l2i=200 mm和σ=0°.在機械手平臺上施加與運動相反方向的恒力為52 N.

非冗余3-RRR機械手恒定工作空間內的直線軌跡和奇異點如圖2所示.對應的移動過程中所需的致動力矩如圖3所示.

圖2 3-RRR聯動的工作空間和直線軌跡Fig.2 Workspace and linear trajectory of 3-RRR linkage

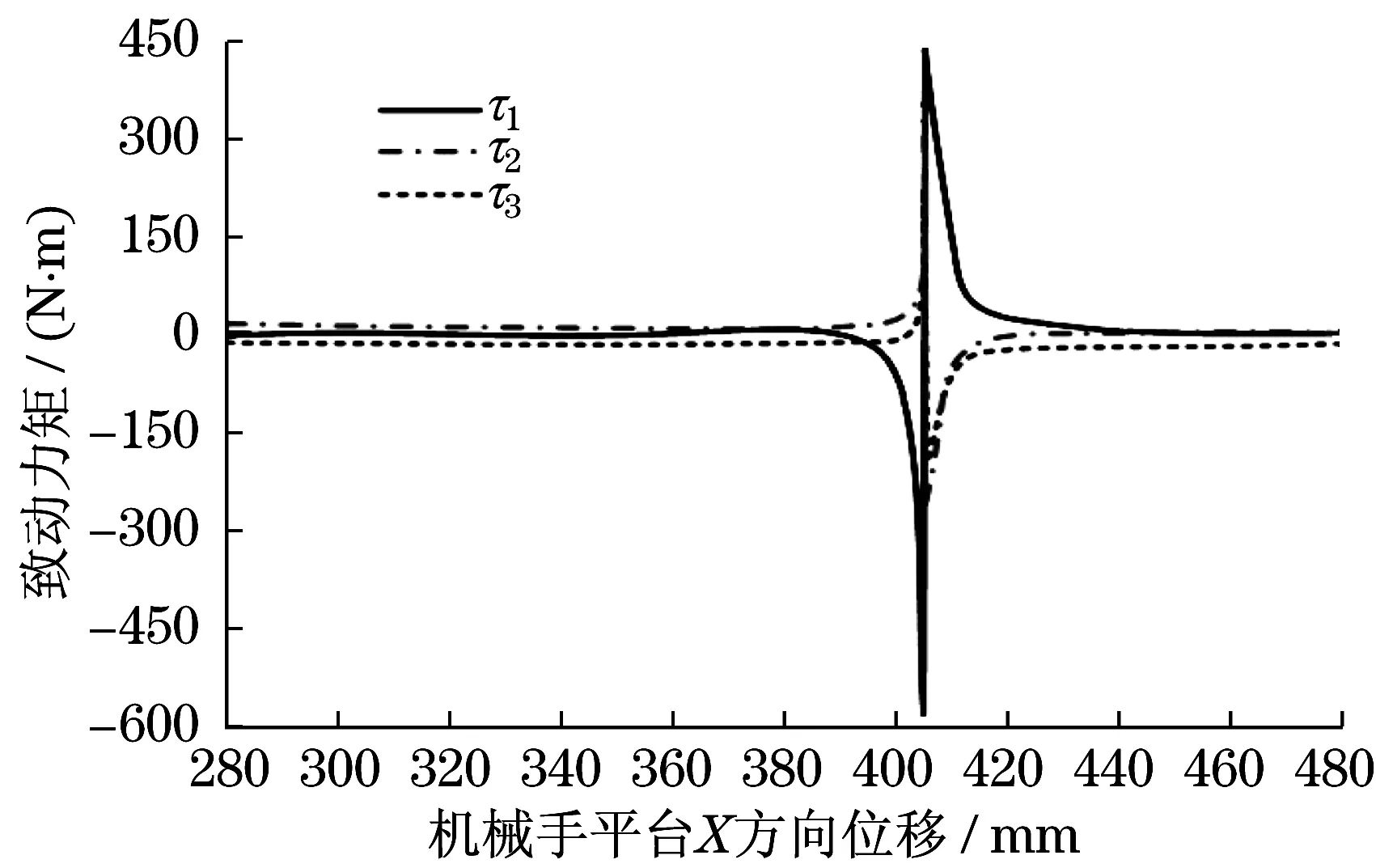
圖3 直線軌跡的3-RRR機械手致動力矩Fig.3 Actuating torque of 3-RRR manipulator with linear trajectory

可以看出,機械手在移動過程中,從點(405 mm,150 mm)移動到點(480 mm,150 mm)通過奇異位形.理論上,關節扭矩在奇點處達到無窮大.圖3在奇點位置關節扭矩為有限值,在-600～450 N·m范圍內變化,因為選擇的步長為1.0 mm.如果采用更精細的位移步長,當機械手完全處于奇異狀態時,計算將失敗.從圖3中可以清楚地看出,非冗余機械手將無法執行期望的軌跡,其需要在奇異點處獲得無限大的致動力矩.

4.2 冗余3-PRRR并聯機械手致動力矩

3-PRRR并聯機械手基礎關節的位移范圍為50～100 mm.當驅動節點的位置發生變化時,定向工作空間和奇異點也同時變化,移動關節工作范圍的選擇方式為:對于移動關節的所有位置,奇異點落在如圖2所示軌跡上的相同區域.

采用相同的直線軌跡,獲得了1-DOKR冗余3-PRRR機械手的移動關節最優位置和最優致動力矩，分別如圖4和圖5所示.其中直線軌跡的關節力矩在每一時間步長上最小.

圖4 1-DOKR冗余3-PRRR機械手移動關節最優位置Fig.4 Optimal position of mobile joint of 1-DOKR redundant 3-PRRR manipulator

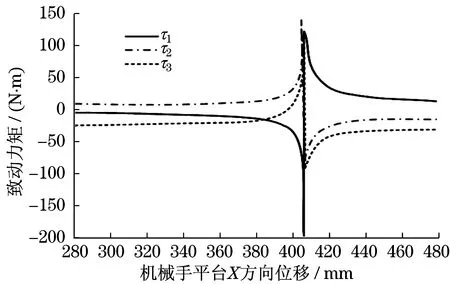
圖5 1-DOKR冗余3-PRRR機械手致動力矩優化Fig.5 Actuating torque optimization of 1-DOKR redundant 3-PRRR manipulator

在采用1-DOKR結構時,移動關節的最佳位置為50 mm,奇異點處的最佳位置達到最大值100 mm.在奇異點處,基礎移動關節的致動力矩變化范圍為-200～150 N·m,對比圖3和圖5可以看出,冗余機械手的關節力矩遠低于非冗余機械手,表明致動力矩被進一步優化.冗余機械手在保持可行的驅動關節力矩的同時,很容易通過奇點結構.與非冗余機械手相比,這種避免奇點的能力是使用冗余機械手的主要優點之一.

進一步研究2-DOKR和3-DOKR冗余3-PRRR機械手的移動關節最優位置，如圖6和圖7所示，對應的最優致動力矩如圖8所示.

圖6 2-DOKR冗余3-PRRR機械手移動關節最優位置Fig.6 Optimal position of mobile joint of 2-DOKR redundant 3-PRRR manipulator

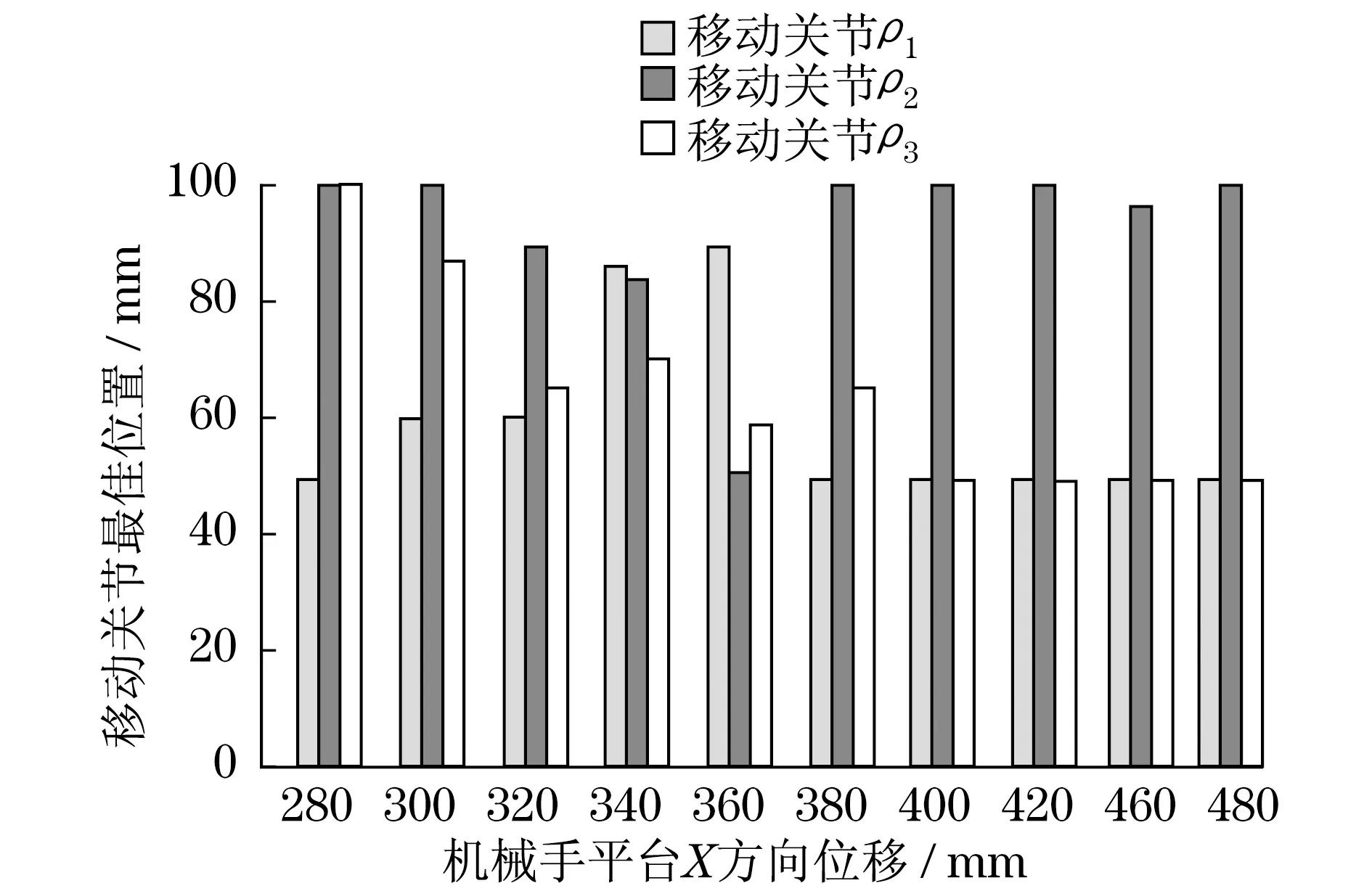
圖7 3-DOKR冗余3-PRRR機械手移動關節最優位置Fig.7 Optimal position of mobile joint of 3-DOKR redundant 3-PRRR manipulator

分析可知,在采用2-DOKR和3-DOKR結構時,相同位置處移動關節的最佳位置相比1-DOKR發生明顯變化,且對應的奇異點由(405 mm,150 mm)變化為(378 mm,150 mm),表明,并聯機械手的奇異位形并非固定不變,隨著自由度和結構的變化而變化.此外,隨冗余度的增大,并聯機械手的致動力矩進一步減小,2-DOKR和3-DOKR結構下致動力矩差異較小,最大致動力矩在-30～30 N·m范圍變化.與非冗余平面并聯機械手相比,致動力矩僅為原來的5.7%,進一步證明了本文提出的基于遺傳算法優化冗余機械手的有效性.

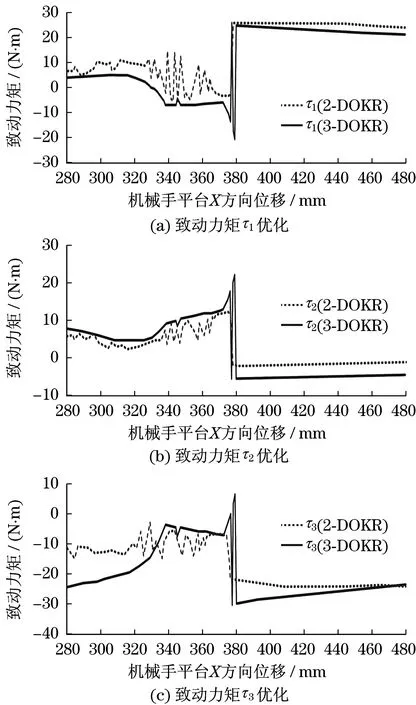
圖8 冗余3-PRRR機械手致動力矩優化Fig.8 Optimizing actuating torque of redundant 3-PRRR Manipulator

5 結論

針對傳統3-RRR平面并聯機械手運動過程中存在奇點,導致致動力矩無限大,無法實現平滑軌跡跟著的問題,采用平面3-PRRR冗余并聯機械手構形.建立了兩種機械手的雅可比矩陣,獲得了機械手的驅動力矩.采用遺傳算法對關節力矩進行了優化,在Matlab/Simulink環境下對兩種機械手直線運動軌跡的致動力矩進行了仿真.結果表明：運動冗余機械手比非冗余機械臂具有更好的性能,冗余機械手執行器所需的最優力矩遠低于非冗余機械手.為了避免選擇移動節點變量邊界的復雜性,本文提出的方法可用靈巧度約束進行擴展.