一種新型搗固裝置及參數確定方法

劉云山

(1.遼寧軌道交通職業學院 機械工程系,遼寧 沈陽 110023; 2.東北大學 機械工程與自動化學院,遼寧 沈陽 110819)

搗固機屬于小型鐵路養護機械,因其機動靈活,常應用在大型養路機械不便應用的線路,如在線路曲率半徑太小或支線等情況下的施工.

本文研究新型液壓搗固機的激振與搗固裝置及參數確定方法[1],提出了搗固裝置動力學參數的確定方法.不同于傳統液壓搗固機的激振與搗固裝置,為提高搗固機的搗固作業質量和效率提供了一條新的有效途徑.

1 激振方式

1.1 搗固機械的激振方式

目前我國搗固機械激振方式有兩種:一種是以偏心塊轉動,產生離心力而帶動搗固鎬振動;一種以偏心軸轉動,通過曲柄連桿機構帶動搗固鎬振動(即所謂強迫振動)[2].

搗固機以偏心塊轉動產生離心力為振動源進行道床搗固,液壓缸同步夾實,目前使用的電動搗固(DZG-350,DDJ-300型等)和小型液壓搗固機(YD-1,YD-2,XYD-1型等)均采用這種振動形式.液壓搗固機為雙導柱框架結構,單缸升降方式.

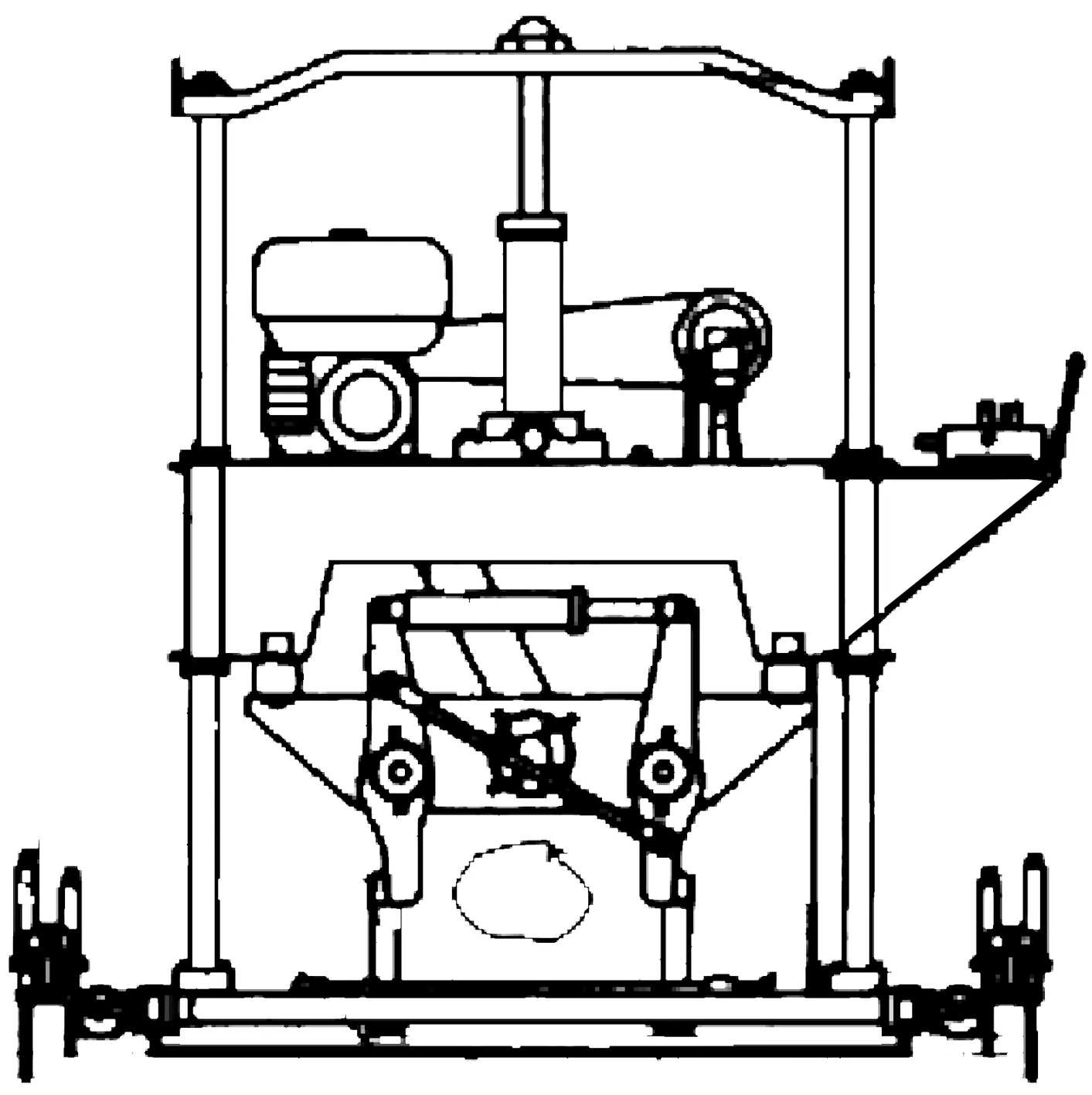
圖1 偏心塊式液壓搗固機示意圖Fig.1 Schematic diagram of eccentric block hydraulic tamping machine

采用偏心軸轉動,通過連桿帶動搗固鎬振動(即所謂強迫振動),再加上異步夾實,是國內外大型搗固機普遍采用的振動方式.它具有固定的振幅,能有效地將動力傳遞給鎬頭;鎬頭的撥動力能隨著道床阻力的增大而增大,而且可以實現反相搗固,有利于搗實枕底道碴[4].在實際搗固過程中大型搗固機通過內外加持油缸進行加持動作,因兩側搗固鎬所受的道床阻力不同,側搗固鎬堅持移動距離也有所不同,所以是異步夾持.這種異步夾持動作,能夠使枕底石砟密實度均勻[5].

大型搗固車采用的是強迫振動和異步夾實的原理,搗固鎬對道碴的作用是搖擺式振動和夾實,但功率大,結構復雜,造價昂貴,不適于鐵路日常頻繁的小規模維護保養.對此,專利[6-7]將強迫振動方式應用于小型液壓搗固機上,但存在的主要問題是由于剛性連接,振動幅值不能調節,因而在需要調整振動幅值的場合應用不方便.文獻[8]指出,在板結道床要求低振動幅值,在松散道床需要高振動幅值.而且在搗固機理方面,利用振動波理論提出了一種推論:在初始的振動、搗固次數增加時,道碴的密實度有所提高,道碴密實度提高到一定程度后,隨著振動、搗固次數的增加,道碴密實度反而減小.由此可見,在道碴足夠密實,搗固力足夠大時,振幅不減小反而降低搗固效果.

1.2 新型搗固機的激振方式

針對現有搗固機傳統偏心塊轉動式激振方式和強迫振動式激振方式的不足,本新型搗固機在設計上提出了一種新型的基于彈性連桿理論的強迫振動式反相位激振與搗固裝置,其目的是既能解決傳統搗固機不能實現反相位振動和異步夾持的問題,又能克服傳統強迫振動激振方式的振動幅值不能調節問題,提高搗固效果,使搗固機的應用更加靈活.

2 新型搗固機搗固裝置的結構及工作原理

2.1 新型搗固機搗固裝置的結構

新型搗固機搗固裝置由偏心裝置、夾持裝置和彈性連桿裝置組成(見圖2).偏心裝置由帶輪、主軸、偏心軸承、主軸軸承座組成;夾實裝置由液壓缸、螺紋活塞連桿組成.彈性連桿裝置由下彈簧、彈簧固定螺紋板、彈簧安裝板、彈簧安裝板固定螺栓、上彈簧組成.

圖2 新型搗固裝置結構三維示意圖Fig.2 Three-dimensional structure diagram of the structure of a new tamping device

2.2 新型搗固機搗固裝置的工作原理

圖2中,主軸由內燃機通過皮帶傳動提供動力,繞軸心順時針轉動.偏心軸承由于偏心安裝在主軸上的原因,其偏心距相當于彈性連桿機構的曲柄長度.在液壓缸與活塞桿沒有相對位移時,液壓缸與螺紋活塞連桿整體相當于彈性連桿機構的連桿.由于偏心距的原因,當主軸旋轉時,彈簧在連桿一端產生位移,彈簧產生形變,這樣就產生了彈力,彈力作用于搗固鎬上,就使搗固鎬產生左右擺動式的強迫振動.由于兩側偏心軸承相位相差180°安裝主軸上,搗固鎬振動的相位也就相差180°,實現反相搗固,有利于搗實枕底道碴.考慮振動頻率較高,振動狀態設為非共振狀態,要求主軸圓頻率為振動系統固有頻率的3～5倍.這就是單質體彈性連桿式振動設計理論的應用.

當液壓系統驅動兩側的液壓缸使活塞桿與液壓缸有相對運動時,相當于增大或減小了彈性連桿的連桿長度,會導致兩搗固鎬繞兩搗固鎬軸承座,有較大的轉動,產生夾持動作.通過設計液壓傳動系統可以實現異步夾持,能自動應對道碴兩側的不同阻力,有效地將石碴重新密實排列于枕軌之下.

（3）注重系統的穩定性與開放性。平臺依附于企業級服務器，系統穩定運行的情況下，盡可能減少和杜絕系統漏洞，在此基礎上豐富系統功能，全面改進穩定性，形成客戶端技術層面上的與用戶需求相貼合的體驗。

3 新型搗固裝置動力學參數確定方法

3.1 新型搗固裝置動力學模型

建立搗固裝置中除去夾持裝置的動力學模型.圖3為動力學模型,屬于單質體彈性連桿式擺動振動模型.該模型由偏心部分、連桿部分和振動質體部分組成.偏心部分為一個半徑為r的圓,r表示偏心裝置中偏心軸承的偏心距,圓心代表偏心裝置中的主軸,設轉速為ω,轉動方向為順時針.連桿部分由一條直線段和一個彈簧力學模型組成:直線段代表彈性連桿裝置中的螺紋連桿,其一端連接偏心部分的圓的圓周上一點,另一端連接一個彈簧力學模型,該彈簧力學模型軸線與所述連桿部分直線段重合;彈簧力學模型代表彈性連桿裝置中的彈簧,設彈簧剛度為k,其另一端連接所述振動質體部分(搗固鎬).

所述振動質體部分為一條長度為(l+h)的直線段,代表彈性連桿裝置中的搗固鎬,即振動質體.該直線段與所述連桿部分直線段夾角大于70°小于90°,其一端與所述連桿部分彈簧力學模型相連,設相連點為A點;另一端為自由端,設該端為D點;在沿所述振動質體部分直線段與A點距離為l處為搗固鎬轉動軸心,設該點為B點,即所述振動質體部分直線可繞B點在所述偏心部分的圓所在平面內轉動;在沿所述振動質體部分直線段與B點距離為p處為C點,該點代表搗固鎬質心.

圖3 單側搗固臂動力學模型Fig.3 Dynamic model of one-side tamping arm

3.2 新型搗固裝置動力學參數確定方法

設搗固鎬所受重力大小為G,作用點為C點,方向豎直向下;設搗固鎬所受彈簧彈力大小為Fs,作用于A點,方向沿所述振動質體部分的直線段的軸線;設搗固鎬所受石料的反力在垂直于搗固鎬方向的分力,即搗固力,為F,作用于D點,方向垂直于所述振動質體部分直線的軸線;設其所受阻尼力對B點的力矩大小與搗固鎬轉速成正比的比例系數,即總阻尼系數,為f,其方向為阻礙搗固鎬轉動趨勢的方向;設搗固鎬相對于軸承座B點的計算轉動慣量為J;設振動的平衡位置為所述振動質體部分直線段豎直時的位置.

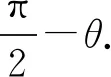
設石料參與振動部分的結合質量為ms,則石料慣性力就是搗固力F,其大小為

(1)

(2)

動力學模型中θ很小,將其進行線性化處理,即sinθ≈θ,cosθ≈1.將其帶入式(2),再將式(1)帶入式(2),則上述方程化簡為

(3)

為標準的振動微分方程,其特解(即強迫振動位移θ的解)為

(4)

式中:A為搗固鎬振動的單側角度參量的振幅;t為時間變量；α為角位移落后于名義激振力矩klsin(ωt)的相位差角.

msh2可視為物料結合質量對B點的轉動慣量.將式(4)帶入式(3),解得A的表達式為

(5)

α的表達式為

(6)

其中,z0為頻率比,即工作頻率ω與固有頻率ω0之比

(7)

而ω0為系統固有頻率,

(8)

ζ為阻尼比,即

(9)

設其激振端(A點)振幅為λ,則

(10)

由式(5)～式(10),可推得本裝置設計參數的確定方法:根據工程需要與工作條件確定基本參數λ,ω,z0,ζ與ms的值.再進行搗固鎬部分的初步結構設計,搗固鎬的結構設計完成后確定J,G,p,l與h的大小.

由式(7)推得固有頻率ω0為

(11)

由式(8)推得彈簧剛度k為

(12)

由式(5)與式(10)推得偏心距r為

(13)

搗固端(D點)的振幅為角參量振幅A乘上搗固端到搗固鎬B點的距離h.從式(5)可以看出,k值改變,A即改變,搗固端振幅即改變.

通過更換彈簧,改變彈簧剛度k,就可以改變搗固鎬的振幅,這也是本搗固裝置與傳統搗固機相比的一大優勢.

3.3 新型搗固裝置動力學參數確定方法實例

本發明實例的設計參數如下:λ=0.75 mm,ω=293.215 rad/s,z0=4,ζ=0.05,ms=2.326 kg,J=0.565 kg·m2,G=130.124 N,p=0.119 m,l=0.245 m,h=0.490 m.

將上述數據帶入式(11)～式(13),算得偏心距r=11 mm,彈簧剛度k=100 226.037 N/m.

4 結語

新型液壓搗固機的激振與搗固裝置工作原理新穎、結構簡單,適用于情況復雜的石砟道床.單質體彈性連桿式振動設計理論的應用,解決了現有搗固機的傳統偏心塊式激振方式和強迫振動式激振方式的不足.新型搗固機動力學參數確定方法,為液壓搗固機的激振與搗固裝置的設計提供了可靠的理論依據.