周邊固支功能梯度圓板的強迫振動分析

劉小飛 龍偲 湘潭大學 湖南湘潭 411105 段啟園 中北大學 山西太原 030051

功能梯度材料是多種物質復合而成的復合材料，近年來材料科學的發展有從單一物質材料發展到多種物質復合而成的趨勢，從均質材料向復合材料發展，而功能梯度材料是復合材料研究的一個重要方向，近三十年才提出，材料學家和力學家以及對功能梯度材料感興趣的科研人員與工程師進行廣泛的研究和精細化的制備。

由于材料組成與性質在橫向的非均勻性分布導致了功能梯度結構的應變在橫向分布的復雜性，表現出與均勻材料結構不同的宏觀特征。從而使得 FGM 結構的彎曲，屈曲和振動與斷裂等宏觀力學行為的分析要比相應的均質材料結構復雜得多。

本文研究功能梯度材料圓板的力學行為，功能梯度材料與均質板的區別是組成與性質隨坐標變化，研究了功能梯度圓板隨著梯度因子的變化，它的固有頻率隨材料參數的變化關系，以及研究了功能梯度圓板受一簡諧力激勵下，材料參數功能梯度因子的變化引起強迫振動的振幅與頻率的影響，此研究可以幫助制備出力學性能良好的功能梯度材料。

1 功能梯度材料簡介

材料作為國民科學技術的支柱之一，材料的進步標志著人類文明的進步，科技技術的快速發展使人們對材料的要求越來越高，特別在航空航天等高技術領域，航空航天發動機對材料有苛刻的要求，不僅需要有金屬材料的強度和韌性，還需要有陶瓷的高熔點和高硬度，但是簡單的層合組成復合材料，在高溫和大溫度梯度下由于熱膨脹將引起剝落或龜裂，為解決此類由熱應力產生材料失效的問題，日本科學家在20世紀80年代后期到90年代初提出了功能梯度材料(Functionally Graded Material，簡稱FGM)的概念，功能梯度材料的概念一經提出快速引起了材料界和力學界的高度注重，迅速成為了材料領域和力學領域的研究熱點。

2 功能梯度圓板的自由振動分析與MATLAB求解

2.1 復合材料圓板的基本假設

本文采用的是薄型圓板，厚徑比的范圍是(小于1/8到1/5)，功能梯度板也可以近似使用基爾霍夫薄板假設。首先圓形薄板作為彈性體，服從連續介質模型的假設，圓板材料是連續分布的，組成物質的質點之間是不存在任何間隙的，我們可以假設認為應力(σ，τ)，應變(ε，γ)和位移(u,v,w)等是連續的變量或者函數，在做數學推導時可以方便的運用連續和極限的操作。

但是彈性體的均勻性假設在此不成立，材料是功能梯度材料，材料的組成結構是呈梯度變化的。

2.2 參數對自然頻率的影響

（1） 參數E0對自然頻率的影響

參數半徑a對自然頻率的影響

泊松比v 對自然頻率的影響

令α=1，半徑a=1,其他變量表達式的數為1，討論厚度對自然頻率的影響

ωn，現由MATLAB作圖模擬厚度變化對自然頻率的影響，厚度h取（0，0.2）符合薄板規定厚徑比小于1/5。

參數冪指數αfalse的大小對自然頻率的影響

ωn∝，厚度0.2,半徑1,厚徑比0.2，其他物理量表達式的值設為1，討論冪指數因子α對自然頻率ωn的影響。

3 簡諧激勵作用下的強迫振動與MATLAB計算

厚度為0.2m,半徑為1m。厚徑比為0.2滿足薄板假設；設頻率比q為0.1，設施加的外力為(N）。其中力的幅值0為100000（N）；阻尼比為0.05。

其 中3h=0.2,v =0.3,E0false=70Gpa,a=1,ρ0=2700kg/m,代入上式求出下表：

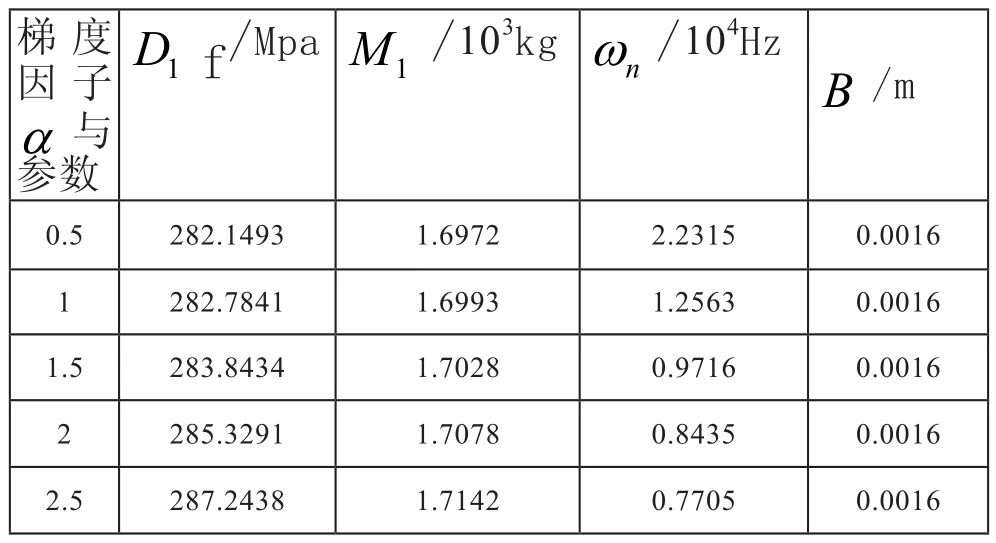
表1 不同梯度因子α對應的參數

設問題的初始條件位移為零，初速度為20m/s,固有頻率不同，阻尼λ和A 值也不同；

λ為：1.0e+03*（1.1157 0.6281 0.4858 0.4218 0.3853）；

A 為： 0.0008 0.0016 0.0020 0.0024 0.0026。

φ1=0將上面的參數代入下面的方程

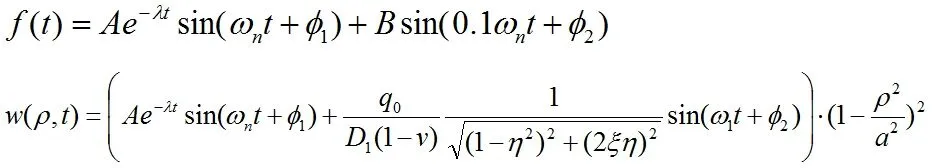
利用MATLAB繪圖如下：

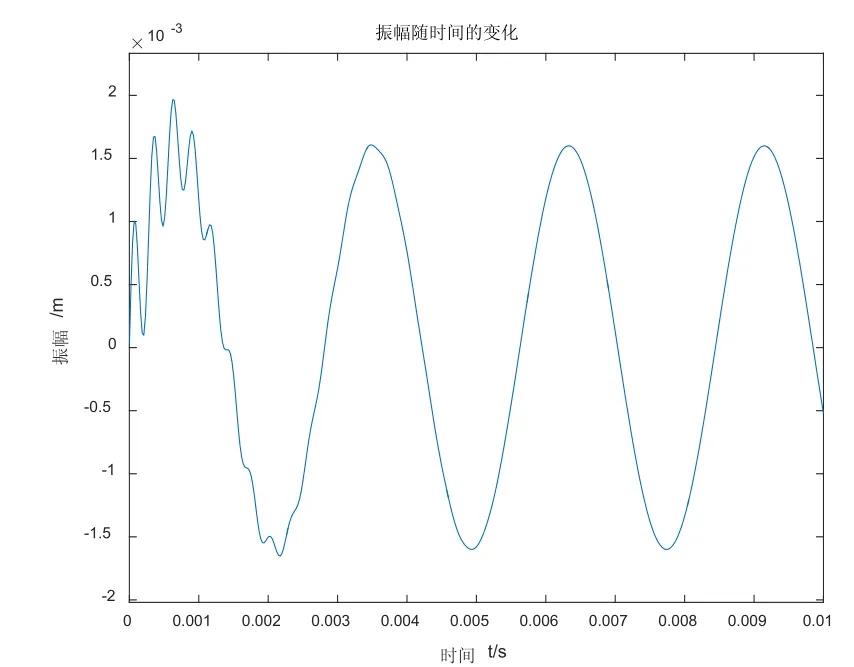
圖3 .1梯度因子α為0.5，振幅隨時間的變化關系

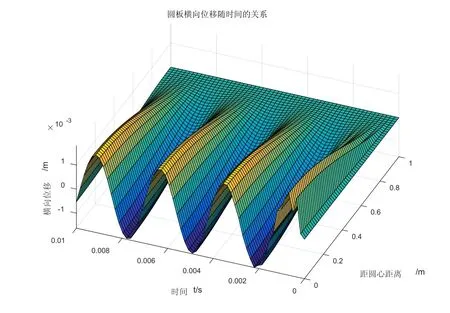
圖3 .6 梯度因子α為0.5軸對稱橫向位移隨時間的變化關系

隨著梯度因子的增大，暫態解振幅越來越大，暫態解的振幅與初速度有關，這里假設初速度為20m/s,梯度因子增大，固有頻率減小，暫態解的振幅越大，穩態解的振幅基本不變，隨著時間的變化，系統趨向于簡諧運動，暫態解衰減到零，系統處于穩態解的振幅函數上，系統越趨近于穩態解。功能梯度板與均質板的強迫振動的區別是梯度因子不為0，在此討論的梯度因子是一個常數，與功能梯度材料的制備有關，一但制成就不再改變，由上節可以看出，功能梯度因子從0.5變化到2.5，固有頻率逐漸減小。研究了初始的0秒到0.01秒的瞬態圖像，外界頻率與固有頻率的關系始終是0.1倍，可以看出從暫態解到瞬態解的過渡非常短暫。

結論

本文分析的是功能梯度薄圓板小變形的振動問題，基于一般連續介質假設，運用了極坐標參考系下的方程，在分析過程中由基爾霍夫假設把縱向位移用橫向位移表達式，由能量法推導了系統的固有頻率，討論了功能梯度圓板的彈性模量，泊松比，密度，厚度，半徑，以及功能梯度指數冪系數αfalse對固有頻率的影響，討論了功能梯度圓板的強迫振動，運用彈性微塊的平衡建立運動微分方程，運用了一個滿足位移邊界條件的振型表達式，表示橫向位移函數，為了使問題簡化，把功能梯度圓板看做是軸對稱振動的，運用伽遼金積分方法，求得振幅關于時間的常微分方程，利用高數知識求解了此微分方程，得到了振幅的表達式，討論了各參數對振幅的影響，最后給出了橫向位移關于時間與半徑的表達式。本文第三章與第四章求得的固有頻率有偏差，可能我用能量法討論時，忽略了縱向運動對動能的貢獻。