高速脂潤滑圓錐滾子軸承保持架動態(tài)穩(wěn)定性分析

吳正海，徐穎強，鄧四二,曹棟波

(1.西北工業(yè)大學(xué) 機電學(xué)院，西安 710072；2.河南科技大學(xué) 機電工程學(xué)院，河南 洛陽 471003)

圓錐滾子軸承作為分離型軸承，因其承載能力大、可承受徑向和軸向及聯(lián)合負(fù)荷、可調(diào)節(jié)性好和壽命長等優(yōu)點，被廣泛應(yīng)用于精密、高速和重型機械設(shè)備中。其中，采用脂潤滑的滾動軸承占比達90%以上[1]，脂潤滑可有效避免潤滑和密封裝置的復(fù)雜性，提高軸承承載、減震和降噪性能。隨著高速轉(zhuǎn)子系統(tǒng)的發(fā)展，對軸承的精度、壽命和可靠性要求越來越高，因此軸承的動態(tài)性能也顯得尤為重要，保持架動態(tài)不穩(wěn)定性往往會導(dǎo)致保持架早期破壞，影響軸承功能的維持。

有關(guān)滾動軸承的動力學(xué)問題，國內(nèi)外學(xué)者已進行了廣泛研究。Walters[2]最早建立4自由度球軸承動力學(xué)模型和6自由度軸承保持架模型，開創(chuàng)性地分析保持架與滾動體的動態(tài)特性。Gupta[3]建立了非潤滑狀態(tài)下圓錐滾子軸承動力學(xué)模型，并開發(fā)了軸承動力學(xué)分析軟件ADORE，對滾動體歪斜、打滑等問題進行了研究。Creju等[4]提出了雙列圓錐滾子軸承的綜合動力學(xué)模型，研究了非Newton流變模型下的拖動等性能，但忽略了保持架的平移運動。胡廣存等[5]基于滾動軸承動力學(xué)理論，建立了油潤滑雙列圓錐滾子軸承動力學(xué)模型，研究了滾動體打滑、歪斜和軸承壽命等動態(tài)性能。郝燁江等[6]分析了軸箱軸承內(nèi)部的載荷分布規(guī)律和影響因素，并利用ABAQUS-explicit對簡化的軸承動力學(xué)模型進行了求解。蓋利森等[7]建立某型高速列車軸箱雙列圓錐滾子軸承三維動力學(xué)模型，并仿真分析了滾動體接觸應(yīng)力變化規(guī)律和保持架的運動穩(wěn)定性。與其它滾動軸承相比，目前對圓錐滾子軸承及其保持架動力學(xué)問題的研究相對較少。

鑒于對脂潤滑圓錐滾子軸承保持架動力學(xué)的研究現(xiàn)狀，本文在考慮圓錐滾子軸承保持架與圓錐滾動體和引導(dǎo)套圈動態(tài)接觸關(guān)系的基礎(chǔ)上，基于脂潤滑彈流潤滑理論和擠壓膜潤滑理論對圓錐滾子軸承保持架全動力學(xué)模型進行了分析，并探討了載荷、速度、預(yù)緊量和保持架材料等對保持架動態(tài)穩(wěn)定性的影響。

1 圓錐滾子軸承保持架動力學(xué)模型

由于圓錐滾子軸承各組件與保持架之間相互作用的動態(tài)不穩(wěn)定性，使保持架運動處于渦動狀態(tài)。為準(zhǔn)確描述軸承各組件的相對位置和運動學(xué)關(guān)系，如圖1所示，建立圓錐滾子軸承慣性坐標(biāo)系o-xyz，坐標(biāo)原點為軸承質(zhì)心，o-x軸與軸承轉(zhuǎn)軸重合。保持架定體坐標(biāo)系oc-xcyczc，原點為保持架質(zhì)心，且隨保持架一起轉(zhuǎn)動。滾動體定體坐標(biāo)系為or-xryrzr，原點為滾動體質(zhì)心，or-xr與滾動體自轉(zhuǎn)軸線重合。

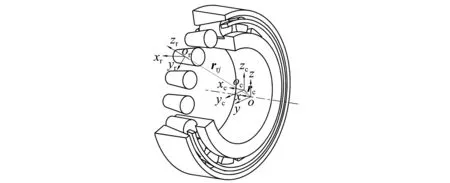
圖1 軸承坐標(biāo)系Fig.1 Bearing coordinate system

圓錐滾子軸承保持架結(jié)構(gòu)與其它軸承保持架相比存在一定的差異，在軸承運轉(zhuǎn)過程中，保持架兜孔和定心表面分別與滾動體和引導(dǎo)套圈直接作用，作用力解析關(guān)系較為復(fù)雜。如圖2所示，保持架在渦動時，兜孔與滾動體將發(fā)生接觸碰撞，在考慮脂潤滑效應(yīng)時，接觸狀態(tài)也會產(chǎn)生變化。同時，保持架定心表面受到引導(dǎo)套圈的作用，以及油氣混合物對表面的黏滯阻力矩。此外保持架也會受到偏心離心力的作用。

1.1 保持架與圓錐滾動體的作用力

圓錐滾動體在保持架兜孔內(nèi)既繞著自身軸線自轉(zhuǎn)，同時又繞軸承轉(zhuǎn)軸公轉(zhuǎn)，并推動保持架一起運轉(zhuǎn)。在保持架和滾動體運轉(zhuǎn)過程中，力作用的主從關(guān)系將隨相對速度和位移的變化而改變。如圖1所示，用卡登角(Cardan Angles)描述保持架和滾動體的剛體轉(zhuǎn)動，在保持架兜孔坐標(biāo)系中，第j個滾動體中心相對于兜孔坐標(biāo)系原點的位置矢量為

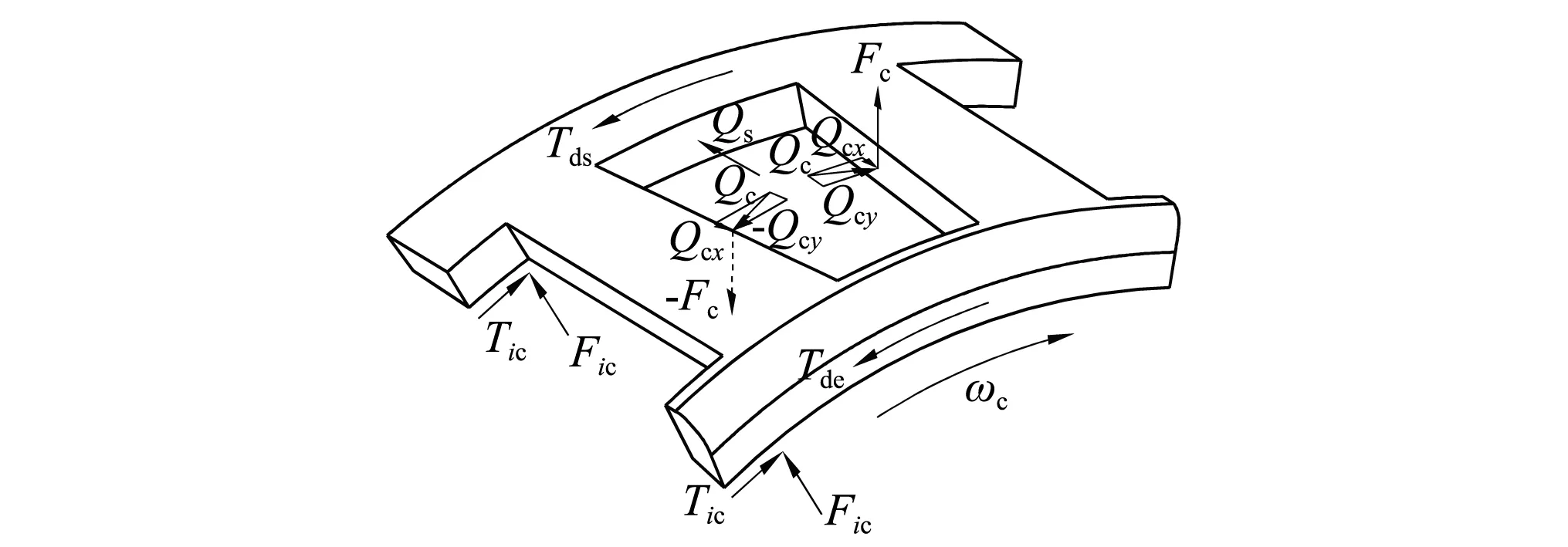
圖2 保持架受力示意圖Fig.2 Sketch of force on cage

rcrj=Bcj(A(rrj-rc)-r0j)-rej

(1)

式中:rc,rrj分別為保持架和滾動體的質(zhì)心在慣性坐標(biāo)系中的位置矢量；r0j為保持架兜孔中心在保持架坐標(biāo)系中的位置矢量(常量)；rej為保持架坐標(biāo)系中滾動體質(zhì)心相對于其中心的位置矢量(常量)；A為慣性坐標(biāo)系到保持架坐標(biāo)系的轉(zhuǎn)換矩陣；Bcj為保持架坐標(biāo)系到兜孔坐標(biāo)系的方向矩陣(常量)。

如圖3所示，第j個圓錐滾動體與保持架梯形兜孔橫梁的間隙δj為

δj=Δδ-rcryj

(2)

式中:Δδ為滾動體與兜孔橫梁之間的初始間隙，Δδ=(Lc-Dw)/2；Lc為兜孔平均寬度；Dw為滾動體平均直徑；rcryj為滾動體中心相對于兜孔中心的周向位移。

假設(shè)Δh0為接觸狀態(tài)轉(zhuǎn)換的油膜厚度臨界值。當(dāng)δj≥Δh0時，滾子與梯形兜孔間僅存在流體動壓作用，而無Hertz接觸作用[8-9]。橫梁與滾動體之間的等效油膜剛度和油膜阻尼分別為[10]

(3)

(4)

(5)

(6)

式中：α為黏壓系數(shù)；uj為卷吸速度；R為當(dāng)量曲率半徑；E為當(dāng)量彈性模量；Le為滾動體有效長度。潤滑脂Herschel-Buikley本構(gòu)方程τ=±(τy+φγn)，其中：τy為屈服應(yīng)力；φ為塑性黏度；γ為剪應(yīng)變率；λn=(2n+1)/(n+1)，n為塑性指數(shù)；η0為基礎(chǔ)油動力黏度；h0j為最小油膜厚度；ξ1,ξ2為與塑性指數(shù)相關(guān)的常數(shù)。

則滾動體與橫梁的接觸力和接觸摩擦力，即油膜動壓力Qcj和油膜剪切摩擦力Fcj為

(7)

(8)

式中：ζ為與潤滑脂流變參數(shù)相關(guān)的變量[11-12]。

當(dāng)δj<Δh0時，滾子與梯形兜孔間存在流體動壓作用，也存在Hertz接觸作用。潤滑脂最小油膜厚度為

(9)

圓錐滾動體與兜孔橫梁之間的Hertz接觸變形為

δhj=Δh0-δj

(10)

存在Hertz接觸時，橫梁與滾動體的接觸力和摩擦力為

(11)

Fcj=μsQcj+Fcehlj

(12)

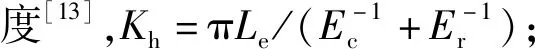
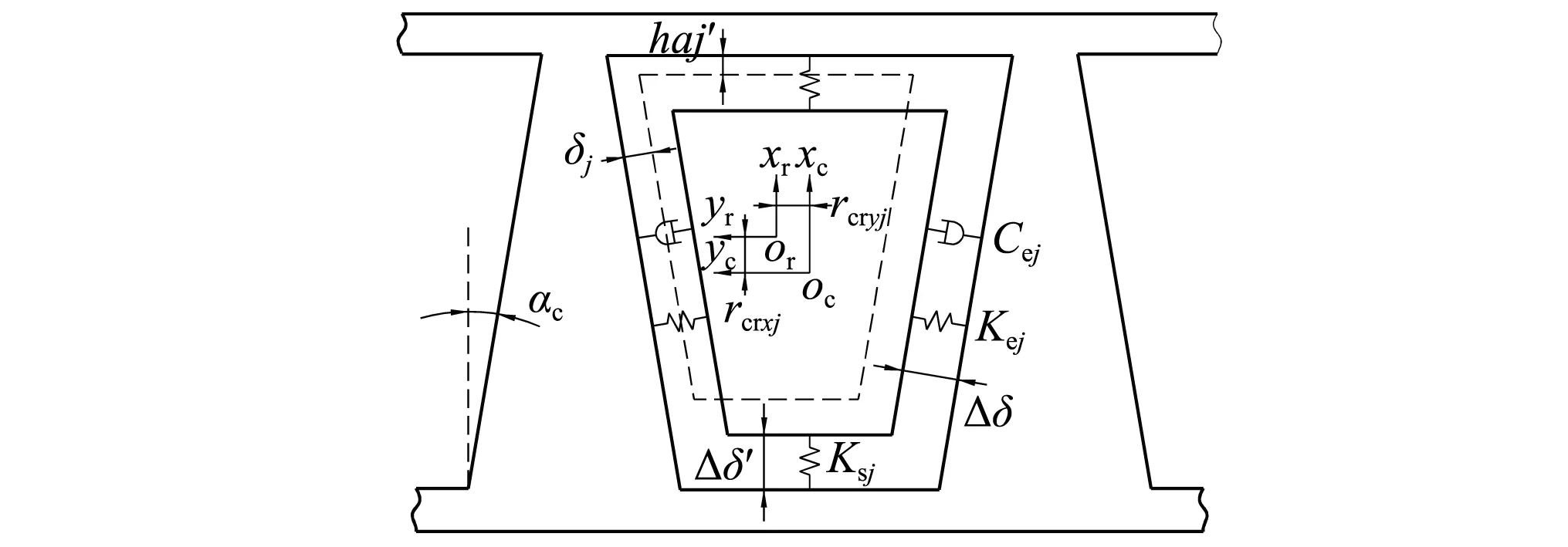
圖3 等效剛度和阻尼Fig.3 Equivalent stiffness and equivalent damping

考慮保持架為6自由度運動，在發(fā)生軸向剛體位移或徑向偏轉(zhuǎn)時，兜孔側(cè)梁將會與滾動體端面發(fā)生接觸，由于側(cè)梁與滾動體平端面的結(jié)構(gòu)特點，在接觸處無法形成彈流潤滑狀態(tài)，但會形成擠壓膜潤滑。假設(shè)兜孔側(cè)梁與滾動體端面的初始間隙為Δδ′；raj為第j個圓錐滾動體中心相對于兜孔中心的軸向位移，raj=rcrxj。若draj/dt≥0，側(cè)梁與滾動體小端端面接觸；若draj/dt<0，則側(cè)梁與大端端面接觸。擠壓膜等效剛度為[16]

(13)

式中:haj為保持架兜孔側(cè)梁至滾動體端面的距離；haj=Δδ′-raj；Δδ′=(Lch-Lh)/2；Lch為梯形兜孔高度；Lh為滾動體高度；Db和Ds分別為滾動體大段和小端直徑；b為保持架厚度。

側(cè)梁與滾動體端面的油膜擠壓力和拖動力為

(14)

Fsj=μsQsj

(15)

式中:μs為側(cè)梁與端面接觸的摩擦因數(shù)。

1.2 保持架與引導(dǎo)套圈的作用力

考慮每個滾動體對保持架的作用力矢量均不相同，致使保持架產(chǎn)生偏心，高速運轉(zhuǎn)又導(dǎo)致保持架動不平衡。根據(jù)保持架定心面和套圈引導(dǎo)面的幾何特點，視潤滑接觸為有限短軸頸軸承潤滑。在徑向平面內(nèi)，保持架與引導(dǎo)套圈接觸作用關(guān)系如圖4所示。

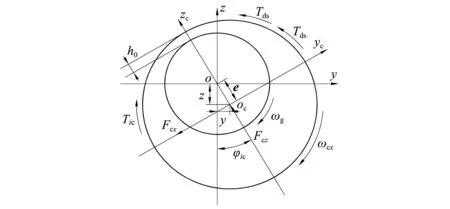
圖4 保持架與引導(dǎo)套圈接觸作用關(guān)系(內(nèi)圈引導(dǎo))Fig.4 Contacts between cage and guide ring

與兜孔橫梁與圓錐滾動體接觸分析類似，保持架定心表面與套圈引導(dǎo)面的間隙Δh′為

Δh′=Δe-‖e‖

(16)

式中:Δe為引導(dǎo)面初始間隙，Δe=(Ry-Rd)/2；Rd為定心面半徑；Ry為引導(dǎo)面半徑；e為徑向平面內(nèi)的位移矢量。

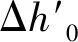
(17)

(18)

式中:k1和k2確定方法與兜孔橫梁和滾動體接觸剛度分析時一樣；u為卷吸速度；Ric為當(dāng)量曲率半徑。

定心表面和引導(dǎo)面的接觸力和切向摩擦力為

(19)

(20)

式中:ωg為引導(dǎo)套圈轉(zhuǎn)速；ωcx為保持架轉(zhuǎn)速。

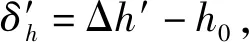
(21)

存在Hertz接觸時，保持架定心表面與套圈引導(dǎo)面之間的接觸力和摩擦力矩分別為

(22)

Tic=μsFic+Ticehl

(23)

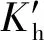
1.3 油氣混合物對保持架的黏滯阻力矩

保持架除受滾動體和引導(dǎo)套圈作用外，其表面還受到軸承內(nèi)腔油氣混合物的黏滯阻力。如圖4所示，保持架端面和錐形表面受到的黏滯阻力矩Tde，Tds分別為[17]

(24)

Tds=τsAcrc

(25)

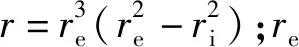
(26)

(27)

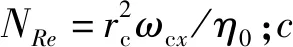
1.4 滾動體受力分析

圓錐滾動體受載荷分析屬于靜不定問題，需借助大量輔助方程解決，采用“切片法”對第j個滾動體進行受力分析，如圖5所示。

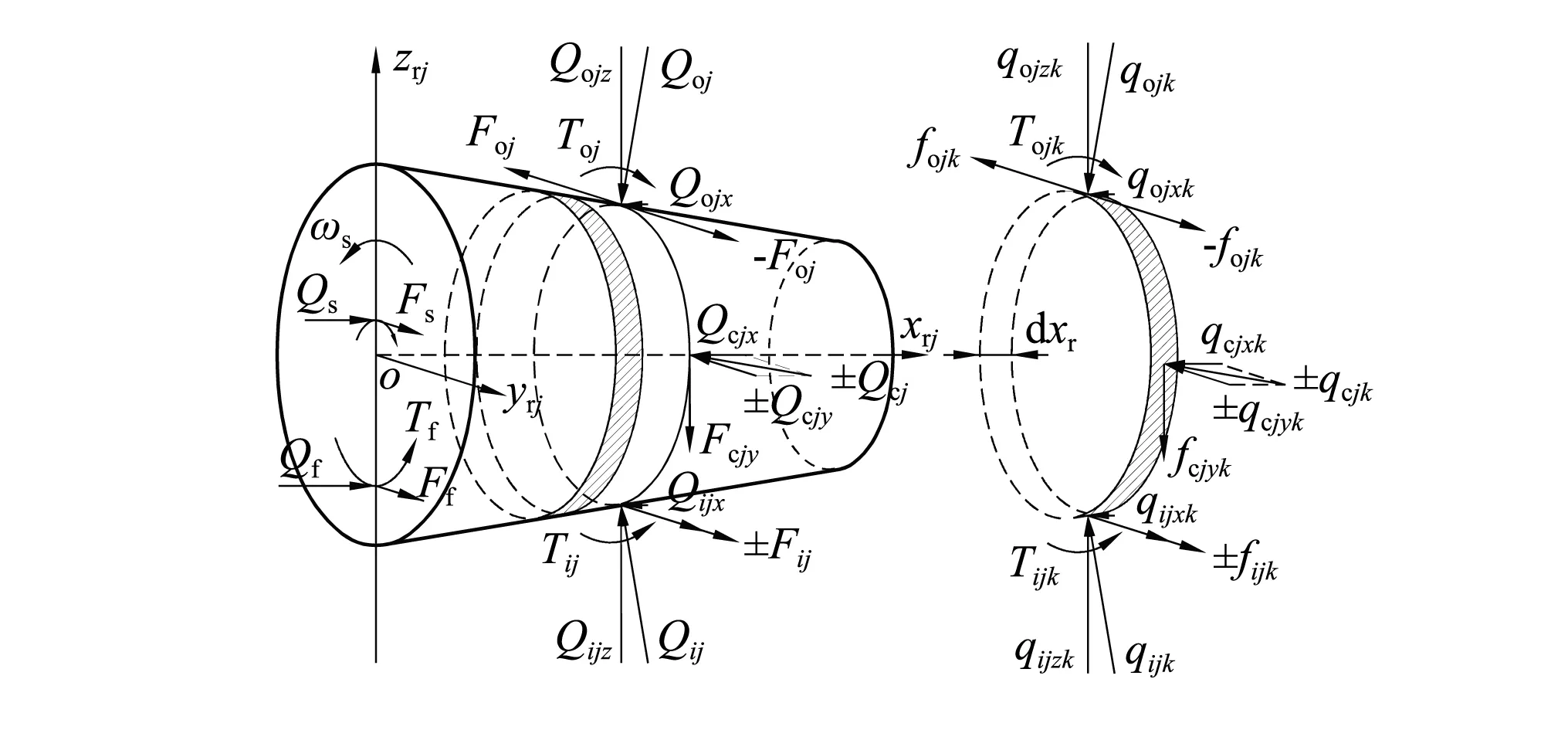
圖5 圓錐滾動體受力分析Fig.5 Force analysis for a tapered roller

假設(shè)使軸承充分潤滑，考慮脂潤滑彈流油膜拖動力Foj(ij)。第j個滾動體的接觸載荷，可由每一片與滾道接觸載荷沿滾動體素線積分得到，即

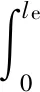
(28)

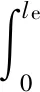
(29)

Ffj=μsQfj=μssinβ(Qoj+Qij)

(30)

式中:Qij,Qoj分別為圓錐滾動體與內(nèi)外滾道的接觸力；Qfj和Ffj分別為滾動體與內(nèi)圈擋邊的接觸力和摩擦力；β為滾動體半錐角。

1.5 保持架動力學(xué)模型

在慣性坐標(biāo)系o-xyz中，保持架平動微分方程為

(31)

式中:M為質(zhì)量慣量矩陣；δ為保持架在慣性坐標(biāo)系的平動位移列向量；F為保持架所受外力列向量

(32)

式中:m=1為保持架兜孔橫梁與滾動體接觸作用力；m=2為兜孔側(cè)梁與滾動體接觸作用力；Fce為保持架偏心離心力。

在定體坐標(biāo)系oc-xcyczc中，保持架旋轉(zhuǎn)運動用歐拉動力學(xué)方程描述

ψ=AN

(33)

(34)

式中:Ix,Iy,Iz為保持架主慣性矩；ω為保持架在慣性坐標(biāo)系中的角速度；N為保持架承受的外轉(zhuǎn)矩，在慣性坐標(biāo)系中將各零件的接觸轉(zhuǎn)矩疊加得到。

(35)

保持架在定體坐標(biāo)系中的角速度ωc與ω的關(guān)系如下，其中B為轉(zhuǎn)換矩陣。

ωc=B-1ω

(36)

(37)

為求解保持架動力學(xué)微分方程，需聯(lián)合滾動體運動微分方程進行求解，在慣性圓柱坐標(biāo)系中列滾動體運動微分方程

(38)

(39)

式中:Mrj為滾動體質(zhì)量慣量矩陣；δrj={rjθj}T為位移列向量；Frj為外載荷列向量；Fej為滾動體離心力。

2 計算結(jié)果與分析

根據(jù)對脂潤滑圓錐滾子軸承動力學(xué)模型的分析，以圓錐滾子軸承ZWZ352226為例，保持架為內(nèi)圈引導(dǎo)，材料為聚酰胺(尼龍66)。采用四階Runge-Kutta法在MATLAB上實現(xiàn)對保持架和滾動體瞬態(tài)響應(yīng)的求解，軸承外套圈固定，內(nèi)套圈轉(zhuǎn)動，各組件的位移、速度和載荷等初始值則通過軸承擬動力學(xué)分析模型得到，以保證求解結(jié)果的收斂和準(zhǔn)確。潤滑脂選用國產(chǎn)聚脲脂[18]，主要流變參數(shù)(30 ℃)：屈服應(yīng)力τy=351.8 Pa，塑性黏度φ=8.44 Pa·sn，黏壓系數(shù)α=4.662×10-2mm2·N-1，塑性指數(shù)n=0.719 6，錐入度λ=33.5 mm，潤滑脂填充量為軸承內(nèi)部空腔體積的1/6。

與圓錐滾子軸承保持架相比，滾動體的徑向運動微乎其微，因此可忽略不計。考慮保持架為內(nèi)套圈引導(dǎo)式，在徑向載荷為21 kN，軸向載荷為10 kN，內(nèi)圈轉(zhuǎn)速2 500 r/min時，分析保持架振動規(guī)律和與滾動體、引導(dǎo)套圈的接觸動載荷，如圖6和圖7所示。

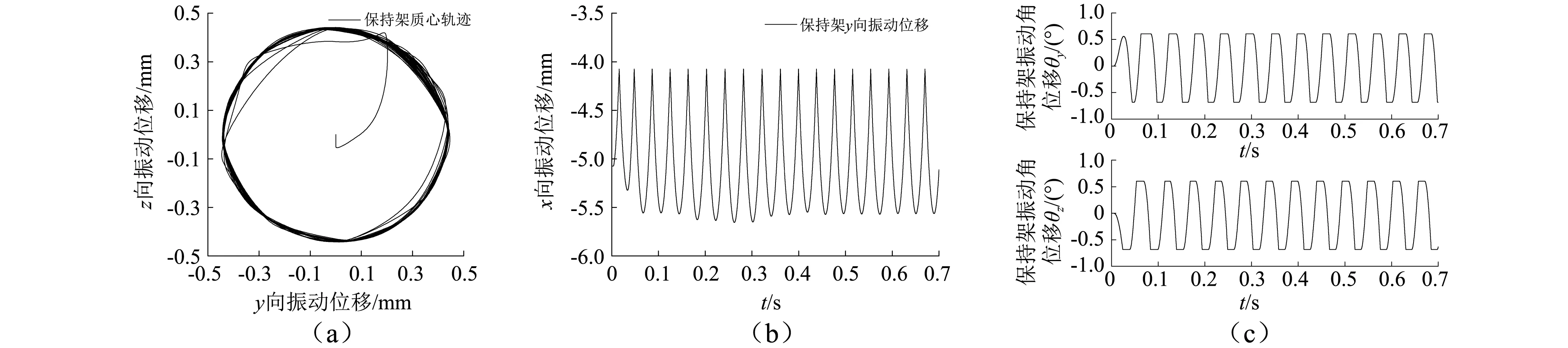
圖6 保持架振動位移Fig.6 Cage vibration displacement

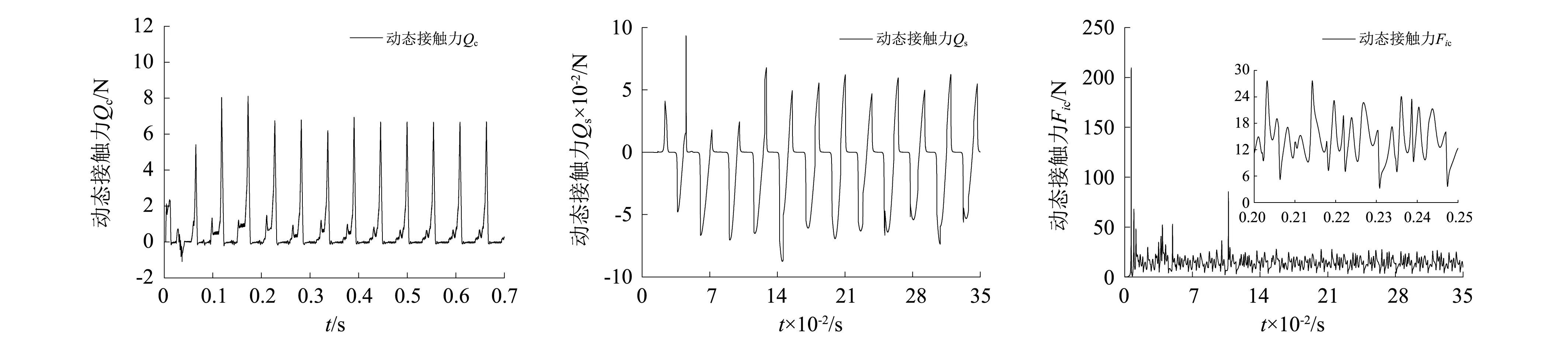
圖7 保持架動態(tài)接觸力Fig.7 Dynamic contact force of cage

由圖6可知，保持架質(zhì)心在徑向平面內(nèi)的運行軌跡近似為圓形，質(zhì)心特殊軌跡的形成主要受引導(dǎo)邊與保持架定心表面，以及保持架偏心離心力的影響；受兜孔內(nèi)滾動體位置的限制，保持架質(zhì)心沿軸線(o-x軸)呈現(xiàn)周期振動，并且兜孔側(cè)梁與滾動體大端的相互作用頻率要高。同樣，受滾動體位置限制，保持架繞o-y軸和o-z軸也呈現(xiàn)周期性的角振動。由圖7可知，在軸承運轉(zhuǎn)過程中，保持架兜孔橫梁與滾動體之間存在高頻接觸碰撞力，載荷呈現(xiàn)明顯的沖擊特征，保持架常見失效如橫梁疲勞斷裂，與這種高頻接觸碰撞有直接關(guān)聯(lián)；對比兜孔橫梁與滾動體的接觸力，側(cè)梁與滾動體的接觸力要小得多，考慮梯形兜孔的結(jié)構(gòu)特征，可推斷保持架在徑向平面內(nèi)的偏轉(zhuǎn)主要受兜孔橫梁接觸力的影響，因此下文主要針對兜孔橫梁接觸力進行分析。相較于滾動體對保持架的作用，內(nèi)套圈引導(dǎo)面對保持架定心表面的高頻作用要大得多，在實際應(yīng)用中，通常保持架與引導(dǎo)套圈之間的磨損，要比滾動體與兜孔之間的摩損要嚴(yán)重。

由圖8可知，保持架角速度在開始時震蕩幅度較大，這時與滾動體的沖擊作用較嚴(yán)重，在進入平穩(wěn)階段后，保持架與滾動體之間仍存在高頻接觸作用，但振動幅值變小并趨于穩(wěn)定。滾動體公轉(zhuǎn)轉(zhuǎn)速在開始時振動幅值也較大，在轉(zhuǎn)入平穩(wěn)運行階段后，振動幅值減小，但比保持架的振動要劇烈，結(jié)果均表明保持架與滾動體在軸承運轉(zhuǎn)時轉(zhuǎn)速并不穩(wěn)定。

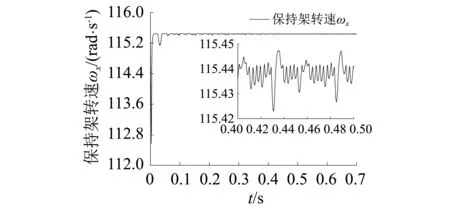
(a)保持架

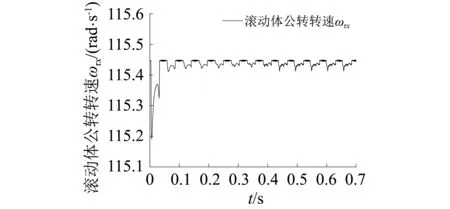
(b)滾動體圖8 保持架和滾動體轉(zhuǎn)速Fig.8 The rotational speed of cage and roller

圓錐滾子軸承各組件之間的動態(tài)接觸力是影響軸承失效和穩(wěn)定性的重要因素，也是軸承設(shè)計需考慮的關(guān)鍵因素之一。如圖9所示，在徑向載荷為21 kN，軸向載荷為10 kN時，分別使軸承內(nèi)圈轉(zhuǎn)速為4 000r/min,5 000 r/min,6 000 r/min，分析轉(zhuǎn)速對保持架動態(tài)接觸力的影響。

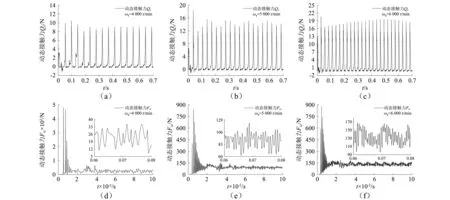
圖9 保持架動態(tài)接觸力Fig.9 Dynamic contact force of cage

由圖9可知，保持架兜孔橫梁與滾動體的動態(tài)接觸力和接觸頻率隨軸承轉(zhuǎn)速的提升而增加，沖擊載荷也會隨之增加。從動態(tài)接觸力的方向可知，在軸承運轉(zhuǎn)過程中，主要是由滾動體推動保持架轉(zhuǎn)動，這是由于軸承內(nèi)腔潤滑脂與空氣的混合物對保持架表面的黏滯阻力矩作用，使得在滾動體公轉(zhuǎn)方向的兜孔橫梁與滾動體的接觸作用頻率更高。同樣，內(nèi)套圈引導(dǎo)面對保持架定心表面的作用力和作用頻率也隨著轉(zhuǎn)速的提升而增加，且接觸力幅值在開始階段要遠(yuǎn)高于平穩(wěn)階段。當(dāng)轉(zhuǎn)速從4 000 r/min升高到6 000 r/min時，平穩(wěn)階段的接觸力平均值由23.059 N增加到131.603 N，因此，軸承轉(zhuǎn)速對動態(tài)接觸力的影響不容忽視。

保持架和滾動體打滑都會影響軸承的服役性能，嚴(yán)重時會造成軸承異常振動、噪音、磨損和燒傷等，保持架和滾動體打滑率為

Sc=(ωg-ωx)/ωg×100%

(40)

Sr=(ωg-ωr)/ωg×100%

(41)

式中：ωr為滾動體公轉(zhuǎn)轉(zhuǎn)速。

在同一載荷條件下，分析轉(zhuǎn)速對保持架和圓錐滾動體打滑率的影響，如圖10所示。由分析結(jié)果可知，隨轉(zhuǎn)速增加保持架和滾動體的打滑率增大，保持架打滑率變化頻率隨轉(zhuǎn)速的增加而降低，滾動體打滑率的變化頻率則隨轉(zhuǎn)速的增加而增。隨著軸承轉(zhuǎn)速的增加，保持架偏心運動將會加劇，且滾動體離心力和陀螺力矩也增大，使得保持架和滾動體的打滑率增加，不利于軸承性能的維持。

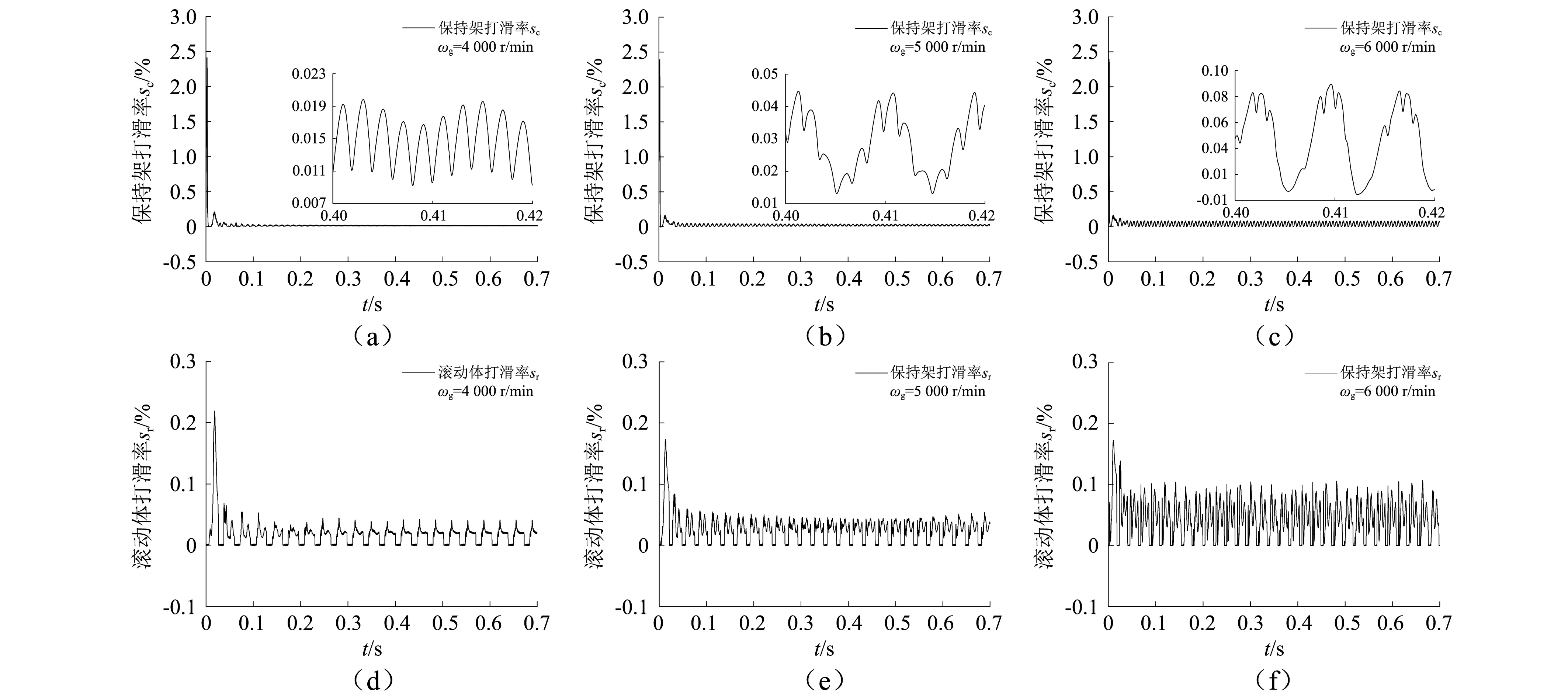
圖10 轉(zhuǎn)速對保持架和滾動體打滑率的影響Fig.10 The influence of speed on cage and roller slippage

根據(jù)上述分析，應(yīng)盡量減小或避免保持架和滾動體的打滑運動，通常軸承打滑出現(xiàn)在軸承非承載區(qū)和高速輕載的工況下，說明載荷對保持架和滾動體的打滑也具有重要影響。如圖11所示，在軸承轉(zhuǎn)速為4 500 r/min，徑向載荷分別為8 kN,14 kN,20 kN時，分析載荷對軸承打滑率的影響。從圖11中結(jié)果可以看出，隨徑向載荷增加，保持架和滾動體的打滑率均明顯降低，在徑向載荷為8kN時，打滑率在經(jīng)過一段時間后才進入平穩(wěn)階段。在分析過程中發(fā)現(xiàn)，當(dāng)載荷小于8 kN時，打滑率甚至?xí)_到20%以上。為解決滾動體和保持架的打滑問題，通常在軸承裝配時會增加一個軸向預(yù)緊量，通過軸向預(yù)緊來改善軸承載荷分布。

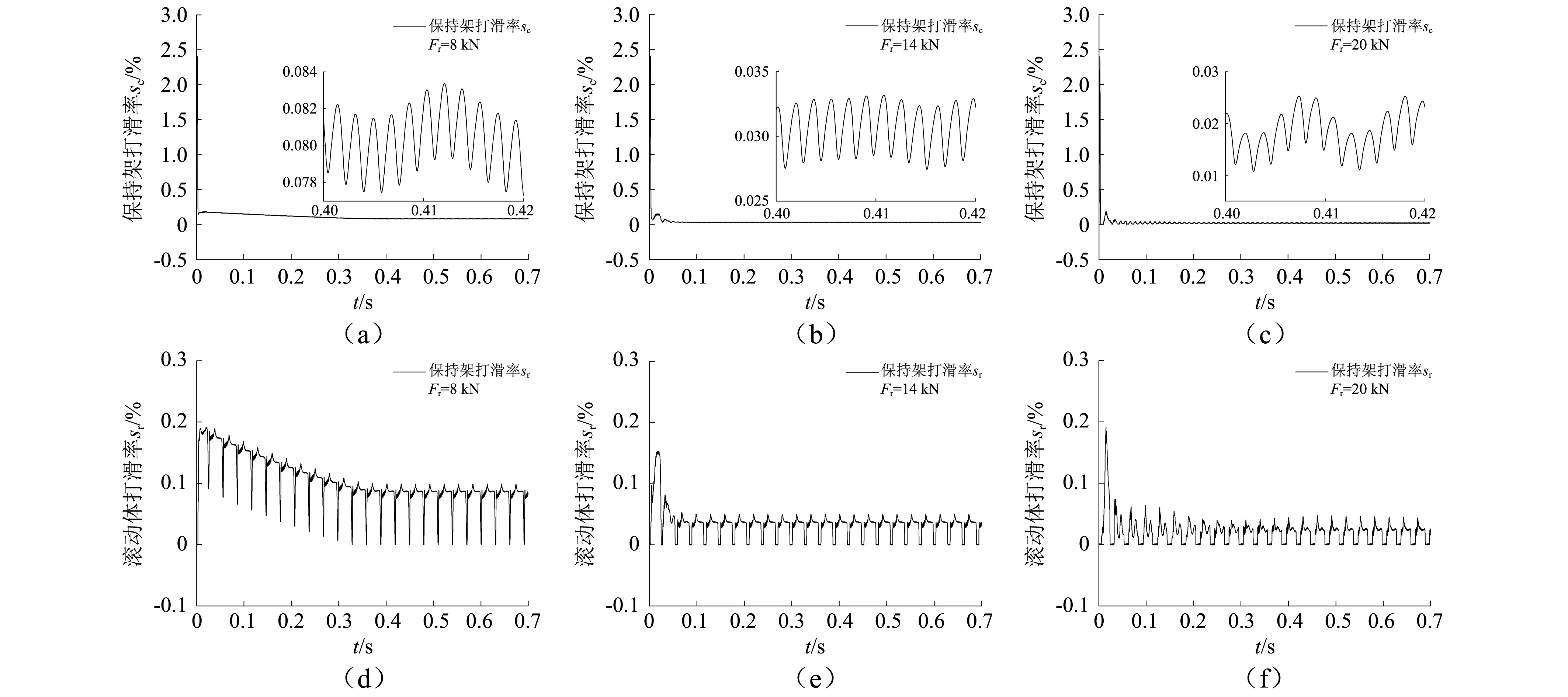
圖11 載荷對保持架和滾動體打滑率的影響Fig.11 The influence of load on cage and roller slippage

如上述分析，圓錐滾子軸承軸向預(yù)緊是保證軸承使用性能的重要途徑之一。如圖12所示，在徑向載荷為21 kN，軸向載荷為10 kN，轉(zhuǎn)速為5 000 r/min時，分別使軸向預(yù)緊量為5 μm,15 μm,25μm，分析保持架打滑率隨預(yù)緊量的變化規(guī)律。由圖12可知，保持架打滑率隨預(yù)緊量的增大而減小，在平穩(wěn)階段，當(dāng)預(yù)緊量增加到25 μm時，打滑率最大幅值由0.025%減小到0.015%，其中隨預(yù)緊量增大，承載滾動體個數(shù)從9個增加到15個(滾子總數(shù)為17個)，也表明承載滾動體個數(shù)對保持架打滑率有重要影響，承載滾動體個數(shù)越多，保持架運行越平穩(wěn)。預(yù)緊量的增加顯然有助于減小保持架打滑率，但預(yù)緊量的過大勢必會降低軸承使用壽命，因此在滿足軸承壽命和使用要求的前提下，合理預(yù)緊量的選取十分重要。

圓錐滾子軸承保持架兜孔間隙Δδ和引導(dǎo)面間隙Δh′的確定是軸承設(shè)計的重要環(huán)節(jié)，間隙大小影響保持架與軸承各組件的潤滑狀態(tài)以及保持架運行的平穩(wěn)性，僅考慮兜孔間隙或引導(dǎo)面間隙變化，在徑向載荷為21 kN，軸向載荷為10 kN，轉(zhuǎn)速為3 500 r/min時，分析間隙對保持架運轉(zhuǎn)穩(wěn)定性的影響，如圖13所示。

由圖13可知，隨兜孔間隙增加，質(zhì)心運動軌跡變寬，軌跡的無規(guī)律跳動也更明顯，說明保持架運行的有序性和穩(wěn)定性降低，同時，隨兜孔間隙增大兜孔接觸力也增大，在開始運轉(zhuǎn)后0.2 s內(nèi)的兜孔平均作用力由1.207 N增加到2.415 N。隨著引導(dǎo)面間隙的增大，保持架質(zhì)心運動軌跡的重疊率增加，軌跡變窄，平穩(wěn)性增加，但保持架與引導(dǎo)面之間的接觸作用力由51.095 N增加到139.828 N，因此對于引導(dǎo)面間隙的設(shè)計需要綜合考慮保持架的穩(wěn)定性和接觸力等因素。

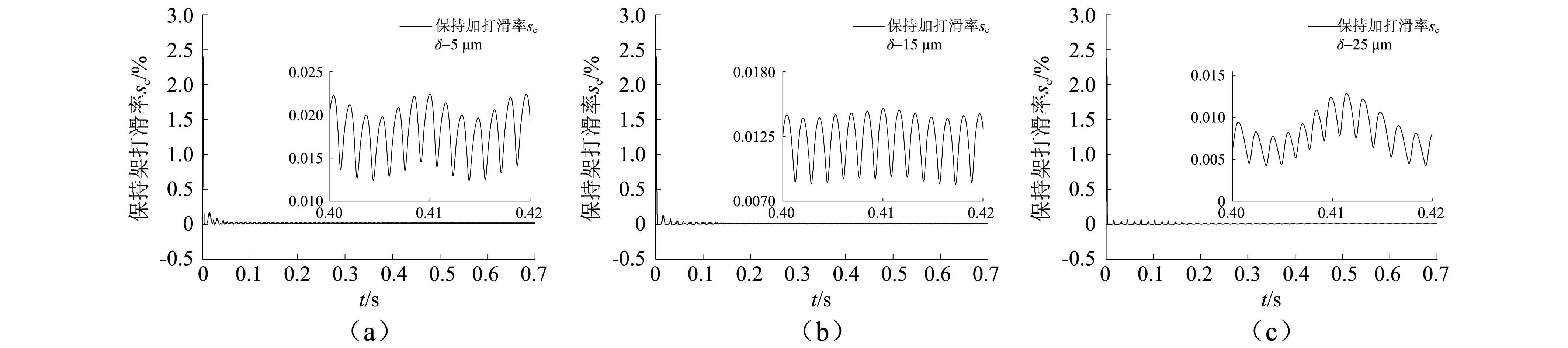
圖12 預(yù)緊量對保持架打滑率的影響Fig.12 The influence of preload on cage slippage

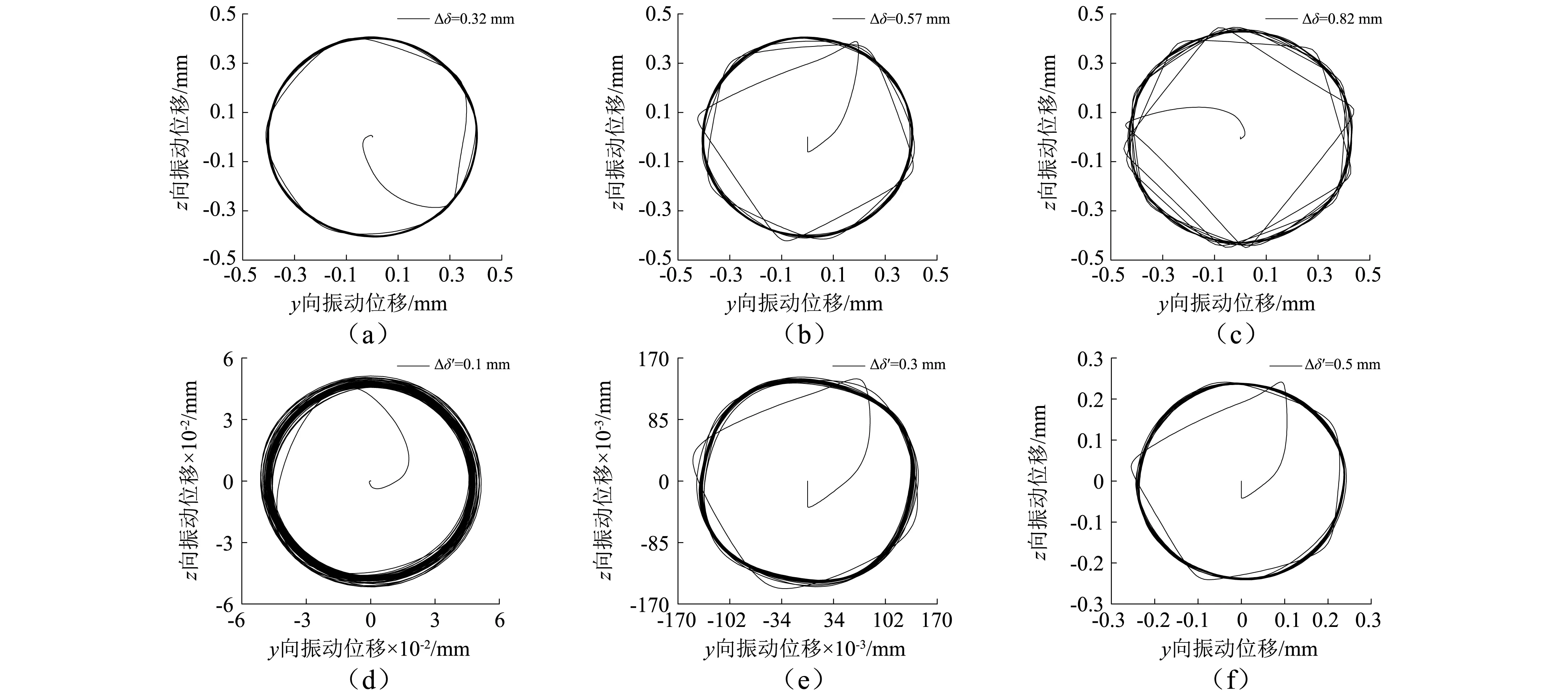
圖13 間隙對保持架運行穩(wěn)定性的影響Fig.13 Influence of clearance on cage stability

通常根據(jù)軸承的服役工況，對選取不同的保持架材料，圓錐滾子軸承保持架材料除聚酰胺外，一般還選取鋼或銅材料，由于各材料的密度和力學(xué)特性均不相同，因此保持架的動體學(xué)特性也將有所差異，在徑向載荷為21 kN，軸向載荷為10 kN，轉(zhuǎn)速分別為1 000 r/min,3 000 r/min,5 000 r/min時，分析不同轉(zhuǎn)速下各材料保持架運行的動態(tài)穩(wěn)定性，如圖14所示。

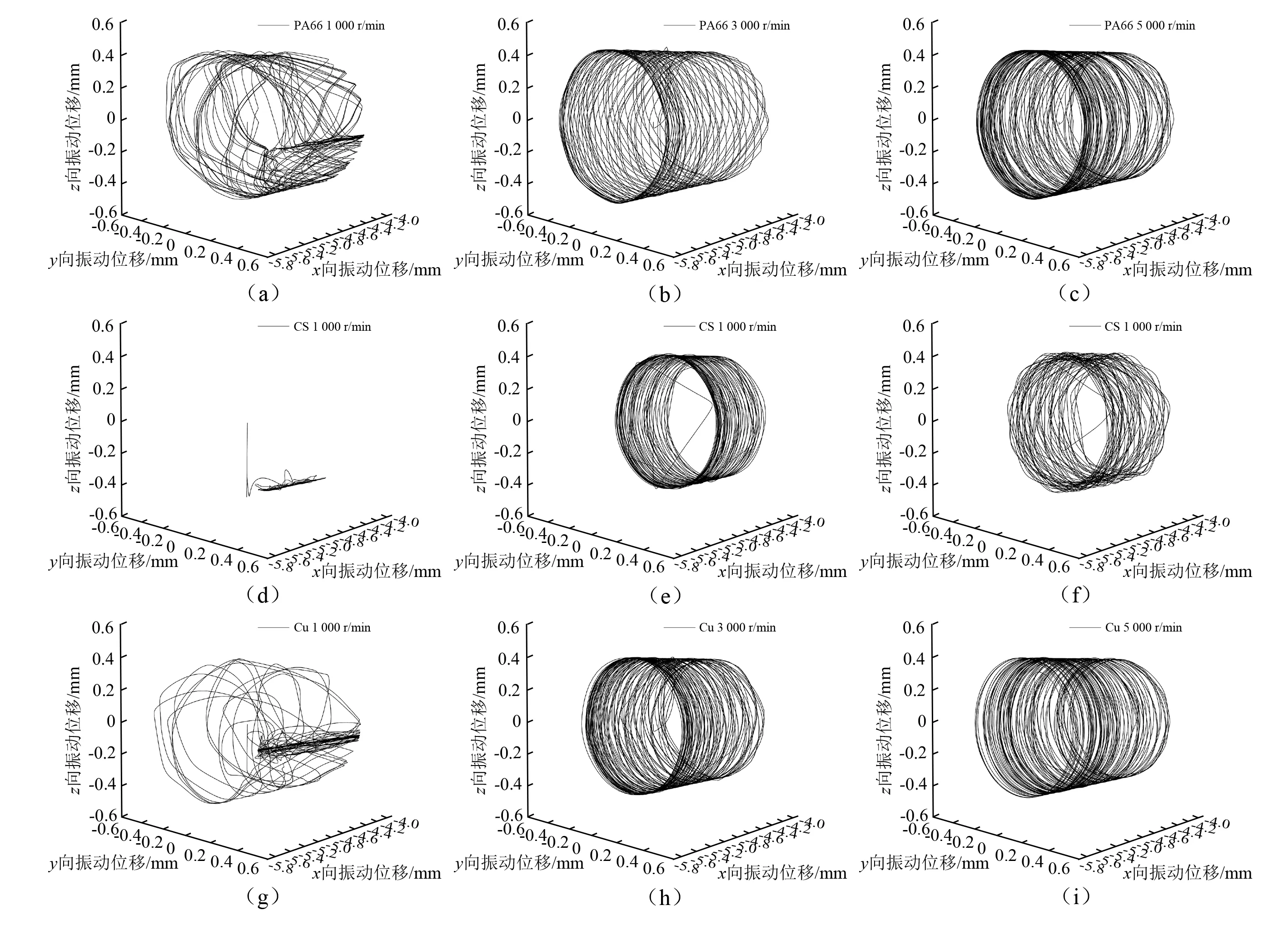
圖14 三種材料保持架的質(zhì)心空間運動軌跡Fig.14 The space motion track of cage mass center for three materials

圖14可知，隨著軸承轉(zhuǎn)速的提高，三種材料保持架的運行平穩(wěn)性也逐漸提高，在速度較高時，質(zhì)心運行軌跡均類似 “圓筒狀”，在低速時，保持架質(zhì)心的運行軌跡均較為紊亂，穩(wěn)定性差。其中，尼龍保持架的徑向振幅相較于其他材料保持架最大，隨轉(zhuǎn)速增加到5 000 r/min，運行軌跡趨于緊湊，軸向竄動也相應(yīng)減小；對于鋼材料保持架，運行軌跡在3 000 r/min時十分緊湊和平穩(wěn)，但隨轉(zhuǎn)速增加，運行軌跡在5 000 r/min時出現(xiàn)紊亂跡象，在轉(zhuǎn)速變化范圍內(nèi)，鋼保持架的軸向竄動最小；對于銅材料保持架，其軸向竄動隨轉(zhuǎn)速增大而增加，但整體平穩(wěn)性和尼龍材料保持架類似。在圓錐滾子軸承設(shè)計中，根據(jù)實際工況對保持架的動態(tài)穩(wěn)定性、抗沖擊、耐磨性和耐腐蝕性能的要求，需綜合各因素選取最合適的保持架材料。

3 結(jié) 論

本文分析了脂潤滑狀態(tài)下圓錐滾子軸承保持架的多體接觸關(guān)系，建立了保持架全動力學(xué)模型，得到如下結(jié)論：

在平穩(wěn)運轉(zhuǎn)狀態(tài)下，保持架與引導(dǎo)套圈接觸作用力要遠(yuǎn)高于兜孔接觸力，且保持架打滑率要低于滾動體打滑率；保持架和滾動體打滑率隨軸承轉(zhuǎn)速升高而增加，隨載荷或預(yù)緊量的增加而減小。

滾動體與保持架兜孔間隙越小保持架動態(tài)穩(wěn)定性越好，且兜孔接觸力也越小；保持架定心面與內(nèi)套圈引導(dǎo)面的間隙越小，定心面與引導(dǎo)面的接觸力越小，但保持架穩(wěn)定性變差；

當(dāng)轉(zhuǎn)速從1 000 r/min增加到5 000 r/min時，尼龍和銅材料保持架的動態(tài)穩(wěn)定性增加，在轉(zhuǎn)速為5 000 r/min時鋼保持架的穩(wěn)定性要次于尼龍和銅保持架。