空間圈套式繩索捕獲動力學建模及接觸碰撞分析

張 龍

(1.中國科學院 太空應用重點實驗室，北京 100094；2.中國科學院 空間應用工程與技術中心，北京 100094)

隨著空間探索的不斷深入，空間機械臂在空間站的組建與維護、衛星的回收與釋放、在軌單元更換及目標載荷轉移等方面的作用愈加凸顯[1-2]。空間捕獲裝置作為空間機械臂最重要的一種末端執行器，其在在軌捕獲任務中扮演著極其重要的角色。空間捕獲裝置數量眾多，國際上主要航天機構都為其空間機械臂設計出相應的末端捕獲裝置，如德國ROTEX機械臂手爪，日本ETS-Ⅶ機械臂末端執行器，以及目前仍處在概念設計的飛網捕獲裝置等[3]，其結構形式、捕獲原理及控制模式不盡相同，按照具體實施抓取部件的特點可將空間捕獲裝置分為剛性捕獲裝置、柔性捕獲裝置和剛柔耦合捕獲裝置。

空間圈套式繩索捕獲裝置屬于剛柔耦合捕獲裝置，其捕獲子系統由固定環、旋轉環和三根柔性鋼絲繩組成。柔性鋼絲繩作為捕獲元件直接與目標載荷接觸，具有大容差、軟接觸的捕獲特點，可以大大提高空間機械臂在軌捕獲的成功率并降低對機械臂和目標載荷的損傷。由于其顯著的優點，已經逐漸的被應用于空間捕獲任務中，如加拿大SRMS末端執行器[4]，哈爾濱工業大學也已經設計出類似的捕獲裝置[5]。

針對空間圈套式繩索捕獲過程中的動力學建模問題，已經有一些學者進行了研究。譚益松等[6]提出了一種基于扭轉阻尼彈簧的平面彎曲柔性鋼絲繩模型，通過在柔性鋼絲繩的末端添加驅動力建立系統的力和力矩平衡方程，該方法簡化了柔性鋼絲繩的建模過程，但是其抗拉特性及接觸碰撞特性未予考慮；李龍等[7]利用牛頓-歐拉混合坐標法建立圈套式繩索捕獲過程中的動力學模型，該文中將圈套式繩索捕獲機構簡單的視為一個可伸縮的剛性圓環，不能全面的反映柔性鋼絲繩的物理特性；潘冬等[8]將柔性鋼絲繩離散成一組單元梁模型，每兩個單元之間通過六維力/力矩連接以充分考慮繩索的拉伸、剪切、彎曲及扭轉等變形特性，基于此建立了各離散段之間的受力與相對位移之間的關系，但是在處理接觸碰撞問題時，忽略了柔性鋼絲繩的抗彎特性；榮吉利等[9]采用絕對點坐標方法描述各向同性柔性鋼絲繩的纏繞運動，并引入繩索與目標間的非線性動力學模型，建立了繩索與目標桿之間的剛柔耦合動力學模型，柔性鋼絲繩的接觸碰撞問題并未考慮；Abiko等[10-11]針對柔性鋼絲繩的接觸碰撞問題均作了大量的地面實物實驗，通過傳感器采集柔性鋼絲繩接觸力信息，并通過經驗公式對接觸力進行擬合。

針對空間圈套式繩索捕獲任務，本文基于拉伸/扭轉彈簧-質點的柔性鋼絲繩離散模型，建立了以離散段長度、偏轉角及俯仰角為變量的柔性鋼絲繩動力學模型，通過引入捕獲機構的約束條件，可模擬空間圈套式繩索捕獲過程中柔性鋼絲繩的運動狀態；同時，引入虛擬彈簧的概念，分析目標載荷與柔性鋼絲繩間的接觸力、壓縮量與柔性鋼絲繩始末端距離的映射關系，建立了目標載荷與柔性鋼絲繩的接觸力模型，可實現對捕獲過程中接觸碰撞力的評估。

1 問題描述

圈套式繩索捕獲裝置主要由3個模塊組成：繩索捕獲模塊，拖動模塊及鎖緊模塊。其具體的工作原理如圖1所示。繩索捕獲模塊的主要作用是抓捕目標載荷限制其在空間內的自由移動，該模塊安裝在支撐殼體上，由固定環、旋轉環和三根柔性鋼絲繩組成。每根柔性鋼絲繩的一端安裝在固定環上保持不動(稱為定點)，而另外一端與旋轉環相連并隨之轉動(稱為動點)。當驅動器驅動旋轉環轉動時，三根柔性鋼絲繩開始隨之運動，形成的封閉捕獲區域逐漸縮小，最終將目標載荷包圍鎖緊。具體的實施步驟1如下[12]：

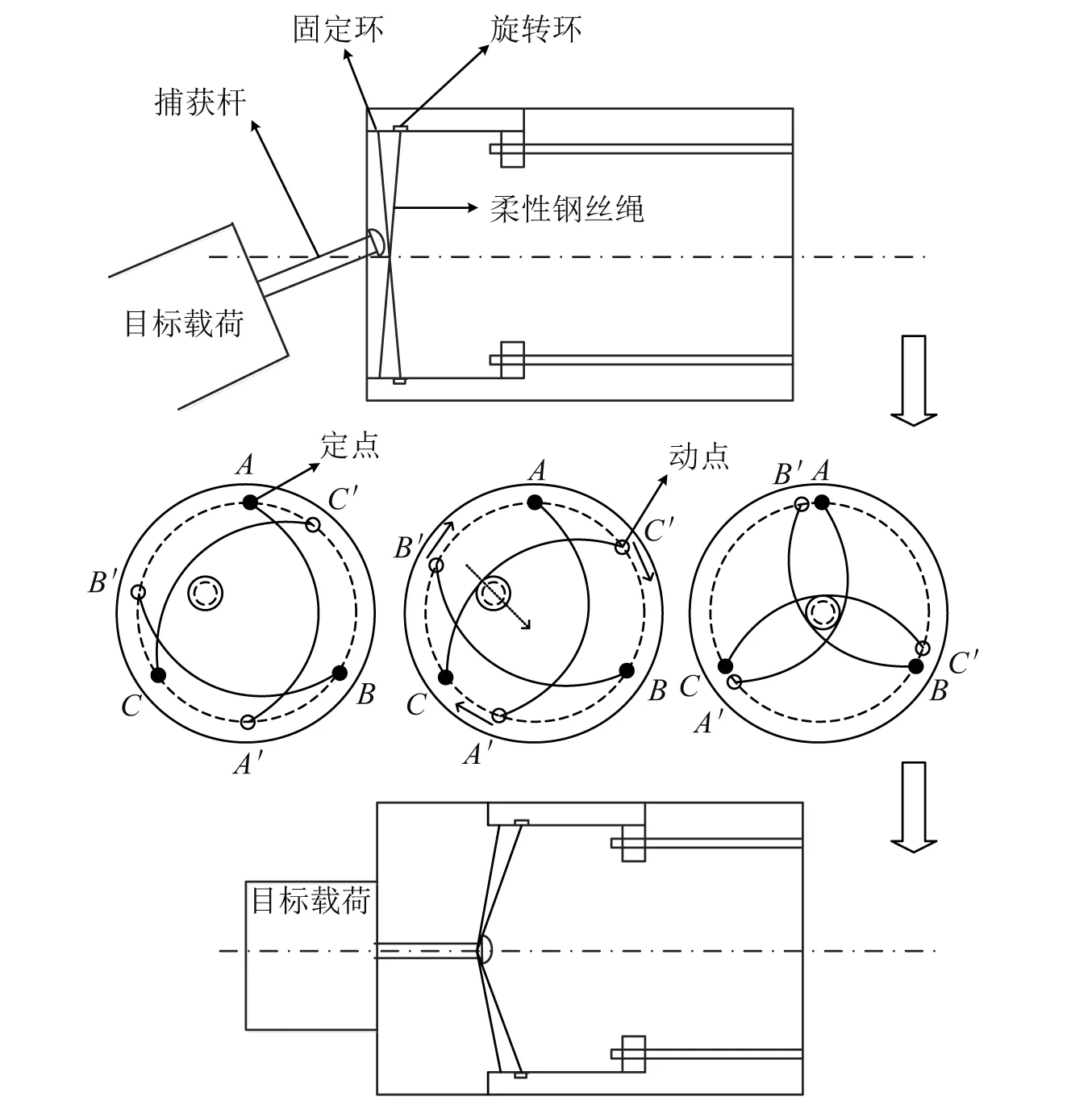
圖1 空間圈套式繩索捕獲過程Fig.1 The process of space snare capture

步驟1空間機械臂攜帶圈套式繩索捕獲裝置接近目標載荷，使目標載荷捕獲桿進入到由三根柔性鋼絲繩形成的捕獲區域內；

步驟2驅動捕獲裝置上旋轉環轉動，則柔性鋼絲繩的動點隨著旋轉環的轉動而運動，使得形成的捕獲區域不斷的收縮，最終將限制目標載荷在空間內的自由移動，在此過程中目標載荷可能與柔性鋼絲繩發生多次接觸碰撞；

步驟3當捕獲區域收縮完畢將目標載荷固定在捕獲裝置的中央，利用拖動系統拖動目標載荷，當目標載荷與捕獲裝置完全貼合時，利用鎖緊裝置將其鎖緊。

2 柔性鋼絲繩動力學建模

在微重力環境下，柔性鋼絲繩與目標載荷之間的接觸碰撞是一個非常復雜的過程，為了求得柔性鋼絲繩與目標載荷之間的接觸碰撞力，首先需要建立柔性鋼絲繩的動力學模型。根據柔性鋼絲繩在捕獲過程中的具體作用和運動特點，可知其需具備兩種典型的物理特性，即抗拉特性和抗彎特性。因此，需要建立兼顧抗拉和抗彎特性的柔性鋼絲繩動力學模型。

2.1 數學描述

將柔性鋼絲繩在空間上離散為一組依次連接的節點，節點編號由繩的一端向另一端依次增加(B1,B2,B3,…,BN)，相鄰節點之間由無質量的拉伸彈簧連接，以此表現出柔性鋼絲繩的抗拉特性。建模時將柔性鋼絲繩所受外力集中施加在各個節點上，根據線密度通過集中質量法可確定每個節點質量

(1)

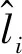
(2)

式中：mtot為柔性鋼絲繩的總質量。

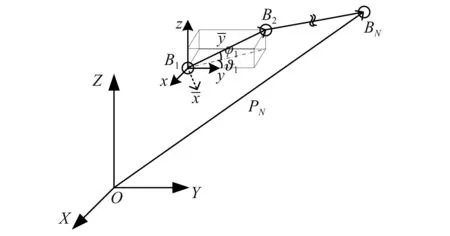
圖2 柔性鋼絲繩坐標系Fig.2 The coordinate systems of flexible cable

2.2 基本運動方程

(3)

(4)

式中：S(ωi)稱為角速度算子矩陣，由式(4)可求得

(5)

若設ωi=[ωix,ωiy,ωiz]T，由于角速度算子矩陣元素具有反對稱性質，則可定義為

(6)

(7)

對式(7)求導可得其旋轉角加速度

(8)

定義第i段柔性鋼絲繩的即時長度向量為li，則第i段柔性鋼絲繩的速度向量可表示為

(9)

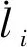
對式(9)求導可得第i段柔性鋼絲繩的加速度向量

(10)

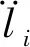
將式(3)、式(7)～式(9)代入式(10)中可得

(11)

式(11)為第i段柔性鋼絲繩的加速度向量在慣性系下的表示，其計算結果相當復雜，二階導數項耦合在一起很難對其進行有效的分離，將其轉換到第i個動坐標系下可得其極簡的表達式，結果為

(12)

以上從運動學層面建立了柔性鋼絲繩的運動方程，下面從動力學角度對其運動特性進行描述。首先對節點Bi,Bi+1進行受力分析，如圖3所示。

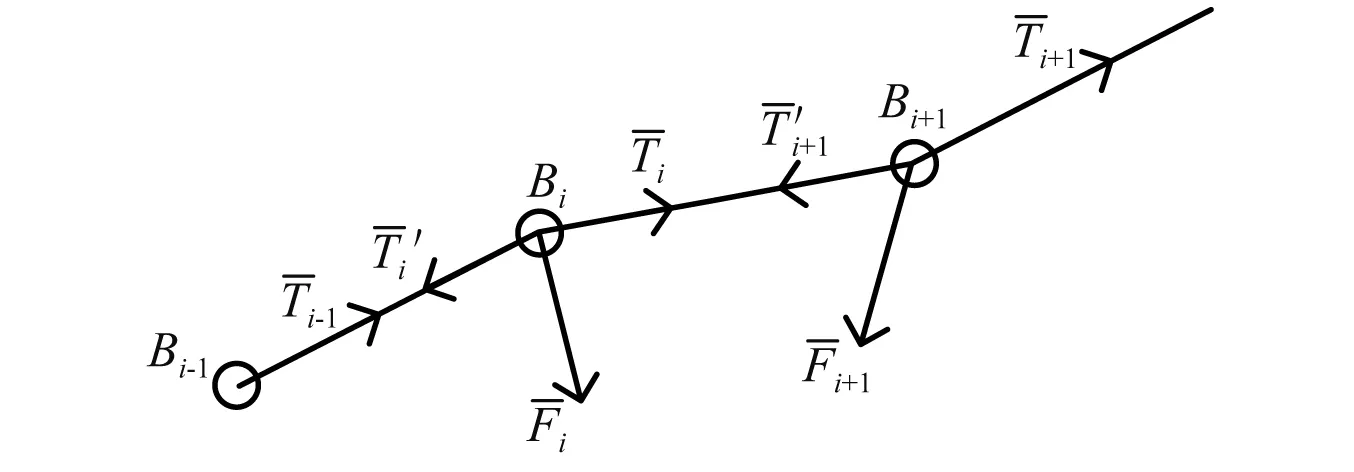
圖3 節點Bi,Bi+1處的受力情況Fig.3 Force analysis of nodes Bi,Bi+1

依據牛頓第二定律可得第i段柔性鋼絲繩的加速度與所受外力的關系為

(13)

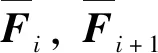
(14)

(15)

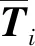
將式(12)和式(13)聯立即可得到以偏轉角?、俯仰角φ及柔性鋼絲繩離散段拉伸長度l為變量的柔性鋼絲繩動力學方程，通過分離二階導數項可得其最終表達式為

(16)

式中：xr=[?i,φi,li]T為柔性鋼絲繩的變量；Hr為柔性鋼絲繩系統慣性矩陣；Cr為系統的非線性項；Pr為系統的勢能項；Fr為等效外力項。其中，i=1～N-1。若i=1，所有下標為i-1的變量取值均為0，若i=N-1，Ti+1,?i+1,φi+1則為0。至此，柔性鋼絲繩的基本運動方程已經建立，由于拉伸彈簧的引入該模型可以反映出柔性鋼絲繩的抗拉特性。

2.3 抗彎特性等效

對于空間圈套式繩索捕獲來說，為保證由柔性鋼絲繩形成的捕獲區域具有盡量大的容差性，鋼絲繩的抗彎特性顯得很重要。柔性鋼絲繩的抗彎特性可以使得捕獲機構擁有較大的有效捕獲區域(見圖4)，上一節中推導的柔性鋼絲繩運動方程中，拉伸彈簧用來模擬柔性鋼絲繩的抗拉特性，本節中在每個節點處加裝一個扭轉彈簧以模擬柔性鋼絲繩的抗彎特性。

圖4 圈套式繩索捕獲有效捕獲區域Fig.4 Effective capture region of snare capture

每個節點處的彎曲力矩大小可由式(17)計算

(17)

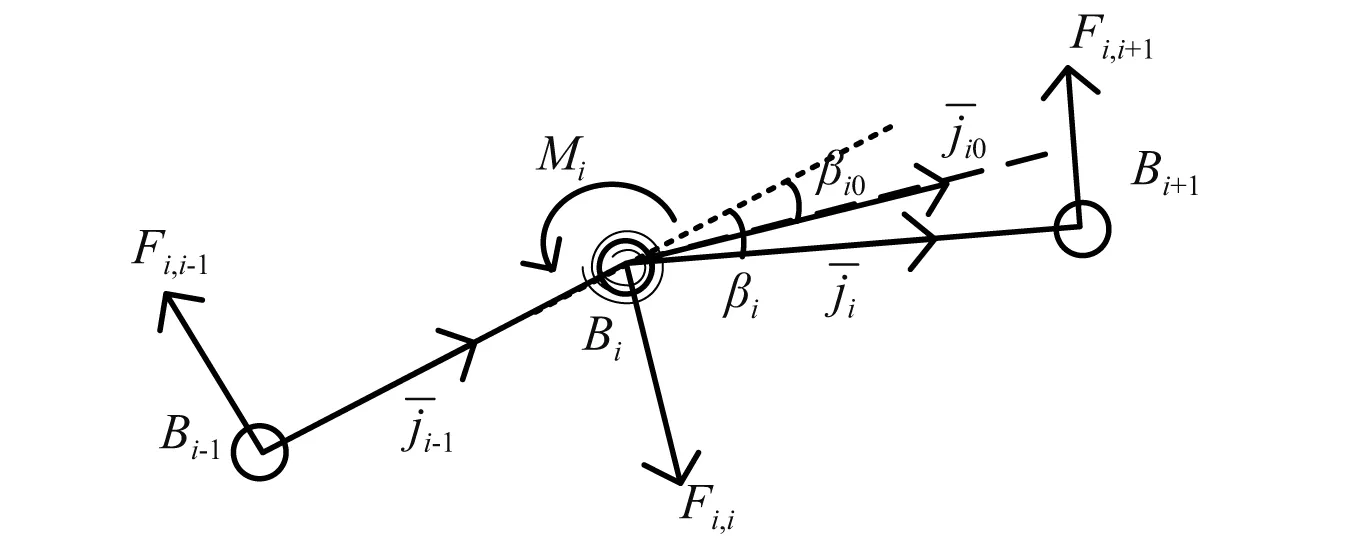
圖5 柔性鋼絲繩彎矩結構等效力Fig.5 The equivalent structural forces of bending moment

等效結構力在平衡節點處彎矩的同時，還需要滿足自身結構力的平衡，即滿足

Fi,i=-(Fi,i-1+Fi,i+1)

(18)

(19)

式中：i=1～N，若i=1，則Fi,i-1=0；若i=N，則Fi,i+1=0；ei,i-1,ei,i+1分別為Fi,i-1,Fi,i+1的單位方向向量可由式(20)計算

(20)

以上計算所得出彎矩等效結構力Fi,i-1，Fi,i和Fi,i+1可以作為外力直接代入式(16)中對柔性鋼絲繩的運動狀態進行求解。至此便建立了完整的柔性鋼絲繩動力學方程，基于拉伸和扭轉彈簧該模型可以反映出柔性鋼絲繩在圈套式繩索捕獲過程中基本的抗拉和抗彎曲的物理特性。

3 圈套式繩索捕獲約束分析

假設圈套式繩索捕獲機構的固定環和旋轉環處于同一平面上，且半徑為Rcm。初始狀態下柔性鋼絲繩AA′的A端安裝在固定環上，A′端連接在旋轉環上，相鄰離散段之間的初始夾角為β1,β2,…,βN-1(見圖6)，其初始處于靜態平衡狀態。為求得柔性鋼絲繩的初始狀態，對其進行受力分析。

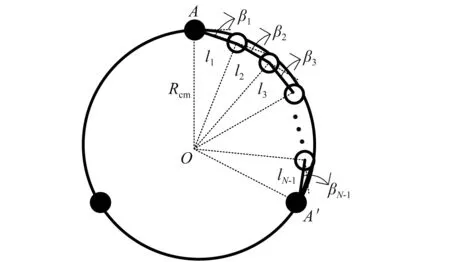
圖6 柔性鋼絲繩初始位置Fig.6 Initial position of flexible cable

依據圖7，對各個節點可列平衡方程

-Ti-1+Ti+Fi,i+Fi-1,i+Fi+1,i=0

(21)

式中：i=2～N-1；Ti-1,Ti為柔性鋼絲繩第i-1段和第i段產生的彈性拉力；Fi,i,Fi-1,i,Fi+1,i為Bi，Bi-1和Bi+1處扭轉彈簧在節點Bi處產生的等效結構力。由于式(21)可以拆分為y和z方向上兩組標量方程組，因此共建立了2(N-2)個靜態力平衡方程。此外，從幾何約束的角度分析，由于柔性鋼絲繩AA′在平面yz內運動，可令?i=0，則以下兩個方程可以建立

(22)

式中：dse為柔性鋼絲繩始末端的距離。

圖7 柔性鋼絲繩初始狀態受力分析Fig.7 Initial force analysis of flexible cable

聯立式(21)和式(22)可得到2(N-1)個方程，同時易知βi=(φi-1-φi)，則基礎未知變量(li,φi)個數同樣為2(N-1)個，方程組可解。初始狀態下的拉伸和彎曲預緊力即可求得

(23)

Mi 0=ktor(βi-βi 0)

(24)

以上便對柔性鋼絲繩在圈套式繩索捕獲機構中的約束及初始狀態進行了分析，同時，由于捕獲裝置的結構特點，動點A′需要跟隨旋轉環旋轉，對于定點A來說，此處由于是鉸接沒有彎曲力矩產生。

4 柔性鋼絲繩接觸動力學建模

4.1 接觸碰撞假設

空間微重力環境下，柔性鋼絲繩與目標載荷之間的接觸碰撞是一個非常復雜的過程，精確的接觸碰撞動力學模型很難獲得，為了簡化建模過程，做了以下幾個接觸碰撞假設：

(1)柔性鋼絲繩與目標載荷之間僅發生單點接觸，并且接觸力僅施加在節點上，事實上，當柔性鋼絲繩離散模型劃分的很細、節點足夠多的時候該種假設是易實現的；

(2)為保證捕獲過程的安全性及操作的可靠性，假設柔性鋼絲繩與目標載荷之間的相對接觸速度很小；

(3)假設接觸碰撞這段極小時間內接觸碰撞力的方向并未發生改變；

(4)與法向接觸碰撞力相比，切向的摩擦力可以忽略不計。

4.2 虛擬彈簧

當柔性鋼絲繩受到外力作用時，根據其受力時的反應狀態，可以假定在柔性鋼絲繩與支撐殼體之間存在一根虛擬的彈簧(見圖8)，彈簧的一端連接在柔性鋼絲繩的節點上，另一端連接在支撐殼體上。由于虛擬彈簧的剛度系數不是常量，接觸碰撞力不能簡單的依據Hertz-阻尼模型計算。經分析可知虛擬彈簧的剛度系數與壓入深度δv及柔性鋼絲繩始末端的距離dse有關，其中壓入深度δv定義為柔性鋼絲繩從初始位置壓入至當前位置在接觸方向上移動的距離。

圖8 柔性鋼絲繩接觸碰撞虛擬彈簧模型Fig.8 The virtual spring model of flexible cable

假設接觸碰撞發生在節點n上，受力如圖9所示。依次針對節點2～(N-1)建立力的靜態平衡方程

(25)

式中：Fc為施加在節點n上的外力。

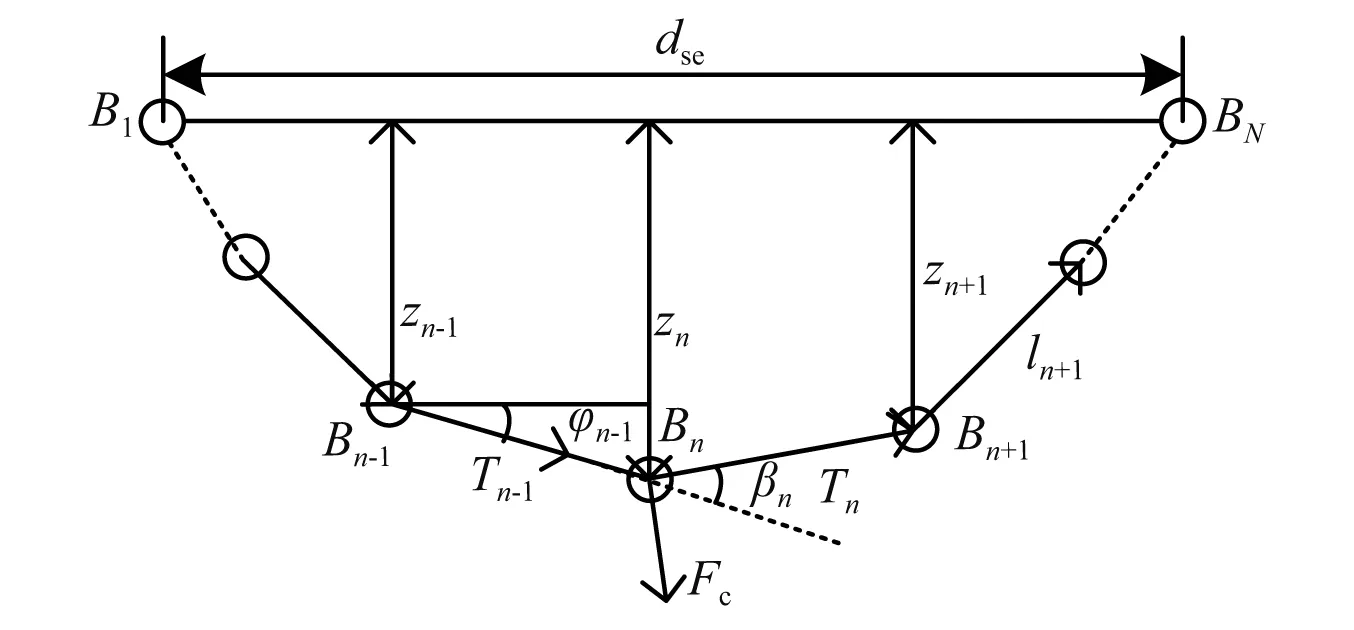
圖9 柔性鋼絲繩受力分析(含接觸力)Fig.9 Force analysis of flexible cable(considering contact force)

式(25)結合幾何約束式(22)可得柔性鋼絲繩在存在外力情況下的平衡方程組。當給出一組Fc和dse時，則對應的壓入深度δv即可求得。柔性鋼絲繩的接觸情況可與彈簧的接觸進行類比，但不同的是柔性鋼絲繩在接觸過程中的剛度不是唯一不變的，它是與壓入深度、柔性鋼絲繩始末端距離有關的量。定義虛擬彈簧的剛度系數為接觸點處法向壓力與對應壓入深度的比值，可采用以下步驟對其進行求解：

步驟1首先設定初始取值范圍dse∈[dmin,dmax]，Fc∈[Fmin,Fmax]，其中，dse的取值范圍由機構的約束決定；而對于外力Fc，其施加的力方向為各個節點處的法向方向，其大小由一個試探性的過程最終確定，最小值為0，假設最大值為FA；

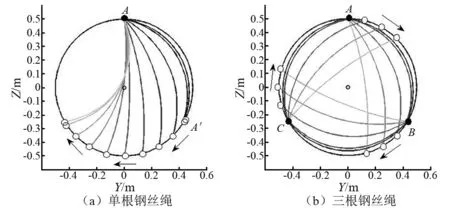
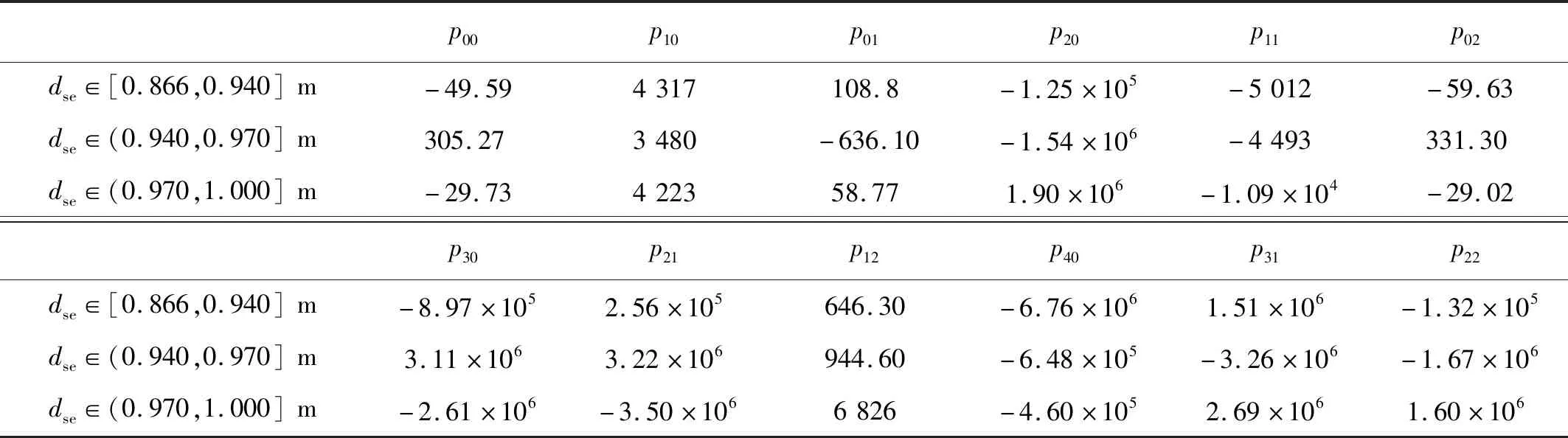
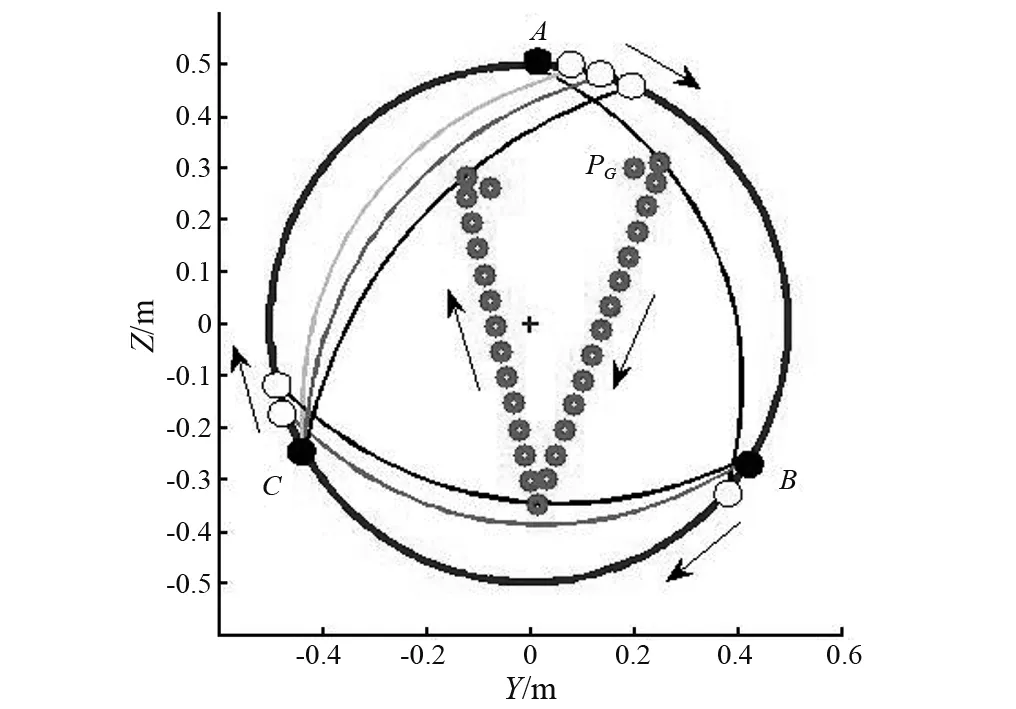
步驟2按一定的間隔在取值范圍內各自取出一組值，[dmin,ds1,ds2,…,dmax]∈R1×m，[0,Fn1,Fn2,…,FA]∈R1×n，dmin

Fc=f(δv)+g(dse)+h(δv,dse)

(26)

式中：f(δv),g(dse)分別為以δv,dse為單變量的多項式函數;h(δv,dse)為多變量耦合函數。值得注意的是，當單一曲面函數擬合精度不足時，可以采用分段函數對數據進行擬合。

依據定義可得出虛擬彈簧接觸剛度系數的表達式

(27)

步驟3在空間圈套式繩索捕獲過程中，當壓入深度、柔性鋼絲繩始末端距離已知時，虛擬彈簧接觸剛度系數即可由式(27)求得。更進一步的，目標載荷與柔性鋼絲繩之間的動態接觸碰撞力即可依據Hertz-阻尼模型計算

(28)

值得注意的是，提出的采用多項式函數擬合方法求取柔性鋼絲繩虛擬彈簧的接觸剛度系數，其具有一定的適用范圍，即dse∈[dmin,dmax]，Fc∈[Fmin,Fmax]。在空間圈套式繩索捕獲過程中只有上述兩個變量在此范圍內時，其計算精度才能保證。如果發現接觸碰撞過程中的最大壓縮位置δv max處的接觸力Fc max=kvδv max大于已經設定擬合范圍的上限值FA時，那么需要重新設定上限值為FB以使得FB>Fc max，然后重復上述計算過程，直到計算結果滿足約束條件。為避免類似的重復性工作，在初始階段可以將Fc的上限值設置的盡量大，但是這會使得在數據擬合階段耗費較多的時間。

5 仿真實驗

5.1 柔性鋼絲繩運動狀態仿真

設定圈套式繩索捕獲機構的固定環與旋轉環的內徑均為Rcm=0.5 m，柔性鋼絲繩初始總長度為ltot=1 m，線密度為ρlin=0.344 kg/m。將柔性鋼絲繩離散為50段共計51個節點，各節點處的拉伸彈簧及扭轉彈簧的剛度系數和阻尼系數分別為ktes=5×104N/m，ctes=1×102N·s/m，ktor=1×103N·m/rad，ctor=1 N·m·s/rad。設柔性鋼絲繩各個節段之間的初始彎曲角度為βi 0=1°。

由上述驅動引起的柔性鋼絲繩運動狀態如圖10所示，圖10(a)表示單根柔性鋼絲繩的運動狀態，圖10(b)則表示圈套式繩索捕獲過程中三根柔性鋼絲繩相互配合的整體運動狀態，圖中黑色圓圈代表柔性鋼絲繩的固定點，白色圓圈代表動點。從圖10中可以看到柔性鋼絲繩的動點處由于與旋轉環固連，會隨著旋轉環做圓弧運動進而帶動整個柔性鋼絲繩運動形成捕獲區域。

圖10 柔性鋼絲繩的運動狀態Fig.10 The motion of flexible cable

5.2 圈套式繩索捕獲接觸碰撞分析

設定目標載荷的質量為mtar=20 kg，末端坐標系下初始位置Ptar=[0,0.20,0.30] m，初始速度Vtar=[0,0.05,0.01] m/s。檢測到目標載荷首先與柔性鋼絲繩AA′上的節點17接觸(節點編號從固定點A開始)。依據文中定義可得節點17處的虛擬彈簧接觸剛度系數擬合方程為

(29)

式中：p00～p22為變量系數，取值如表1所示。

表1 節點17處接觸剛度擬合方程系數Tab.1 Coefficient of fitting equation of node 17 contact stiffness

設定阻尼系數為cv=1 N·m·s/rad，則目標載荷與柔性鋼絲繩接觸過程中的動態接觸力可由式(28)計算。接下來目標載荷與柔性鋼絲繩BB′，CC′的接觸碰撞采用上述類似的方法，在已知柔性鋼絲繩始末端距離dse及壓入深度δv的情況下，即可求得柔性鋼絲繩與目標載荷之間的接觸碰撞力曲線，整個捕獲運動過程如圖11所示。圖12為柔性鋼絲繩與目標載荷接觸碰撞時目標載荷受到的碰撞力，目標載荷第一次與柔性鋼絲繩AA′接觸發生在約1.10 s，持續時間約為0.79 s，-y和-z方向的最大接觸碰撞力為2.78 N和2.37 N。第二次與柔性鋼絲繩BB′的第22個節點發生碰撞在約15.51 s，持續時間約為0.75 s，y和z方向的最大接觸碰撞力為0.17 N和4.24 N。第三次與柔性鋼絲繩CC′的第31個節點發生碰撞在約29.12 s，持續時間約為0.90 s，y和-z方向的最大碰撞力為2.36 N和2.65 N。

圖11 圈套式繩索捕獲接觸碰撞過程Fig.11 The contact during snare capture

圖12 圈套式繩索捕獲過程中接觸力Fig.12 The contact force during snare capture

6 結 論

空間圈套式繩索捕獲裝置由于具有大捕獲容差、高剛性連接及軟接觸的優點，已經逐漸被應用于太空中大型航天器的捕獲任務中。本文針對空間圈套式繩索捕獲動力學及接觸碰撞問題進行研究，提出了一種基于拉伸/扭轉彈簧-質點的柔性鋼絲繩動力學建模方法，可以表現出柔性鋼絲繩抗拉及抗彎等基本物理特性，可以模擬空間圈套式繩索捕獲過程中柔性鋼絲繩的運動情況；提出了一種基于虛擬彈簧的柔性鋼絲繩接觸力建模方法，可以計算目標載荷與柔性鋼絲繩間的接觸碰撞力。研究成果可以實現對空間圈套式繩索捕獲過程的預演，及時發現捕獲任務中潛在的問題，避免風險。