基于顆粒阻尼的PCB動力學與電路聯合設計研究

肖望強，余少煒，林昌明，劉利杰

(1.廈門大學 航空航天學院，福建 廈門 361000；2.北京華航無線電測量研究所，北京 100013)

為滿足我國空天作戰概念的創新，導彈武器正向跨域化、高速化、多用化方向發展。導彈的電子系統能夠實現導航、通信、目標識別、跟蹤定位等為一體化多功能技術，一旦內置的電子設備出現故障，造成導彈的失誤，將會產生災難性的后果。PCB(Printed Circuit Board)是導彈電子設備的重要組成部分，圖1為PCB在導彈中的應用，在導彈受到發射階段的高強度振動和沖擊下，導彈內電子組件會產生嚴重的動態響應。據統計，在機械力，電磁力，環境等造成電子設備失效的因素中，27%是振動因素造成的[1-2]。傳統的減振措施有很多，應用較廣的減振元件一般采用橡膠隔震器。但橡膠隔震器存在以下問題：工作溫度范圍較窄；隔斷熱傳導路徑，帶來熱設計困難；橡膠材料容易老化，需要定期更換等[3-5]。為解決橡膠減振器的弊端，適應未來產品發展需求，急需開發設計一種不隔斷傳熱路徑，適用溫度范圍廣，適用頻帶寬，不引入直線位移和角位移的新型減振技術。

圖1 電路板在導彈中的應用Fig.1 Application of circuit board in missile

顆粒阻尼技術是一項振動被動控制的新技術，該技術能夠在高低溫、輻射等惡劣環境下提供有效的寬頻減振，并具有減振效果顯著、各向同性、不增加線位移、可靠性高、不改變原結構等諸多優點[6-10]。將顆粒阻尼應用在PCB上，通過顆粒在腔壁中的摩擦與碰撞將動能耗散為熱能[11-15]，能有效的減少其在運輸與使用過程中振動與沖擊的影響。

傳統的PCB設計一般只考慮電路板圖形的布線密度、導線精度等問題，但沒有過多考慮電路板的振動問題。因此，本文提出一種新型PCB動力學與電路聯合設計方法，這種聯合設計的核心就是在電路設計之前先進行動力學分析，確定電路板的振動敏感區域，通過敏感點進行阻尼器的設計和阻尼顆粒參數的優化，最終完成電路體系的設計。本文的聯合設計的方法能達到有效的減振效果，特別對于導彈、艦艇的PCB在惡劣振動環境下具有十分重要的理論意義和工程價值。

本文基于PCB動力學特性進行分析，確定阻尼器的安裝區域并在非敏感區域設計電路，在敏感區域安裝顆粒阻尼器。通過離散單元法計算顆粒的系統耗能，優化顆粒的粒徑大小、填充率等參數，提出有效的減振方案。通過與PCB試驗相結合的方法，研究顆粒阻尼的配置方案對PCB運動特性的影響規律。

1 PCB的動力學設計

1.1 模型建立

PCB的組件主要由電路板和電子元器件經由機械與電氣連接成為一個整體，結構較為復雜。基于本文研究，針對計算模型進行簡化，忽略PCB上的元器件對PCB的剛度與質量影響，將其視為薄板處理并刪除無關緊要的非承載結構。PCB的尺寸為192×179×2(mm)，材料為FR- 4，密度為1.9×103kg/m3，彈性模量為1.11×1010Pa，泊松比為0.28，三維模型如圖2所示。

基于ANSYS有限元軟件，模型采用實體單元SOLID185，用于構造三維固體結構，把特性參數賦予PCB各部分并劃分網格后，建立的有限元模型如圖3所示。

圖2 電路板三維模型Fig.2 Circuit board three-dimensional model

圖3 有限元模型Fig.3 Finite element model

1.2 模態分析

本文針對PCB的聯合設計構想，先根據機箱尺寸與元器件的規格確定PCB的尺寸，通過有限元方法確定PCB的模態敏感點區域。模態參數為結構動力特性的優化設計提供依據[16-17]，為實現下一步PCB的電路設計奠定基礎。由lagrange方程可得一個n自由度的系統運動方程為

(1)

式中：[M]，[C]，[K]分別為系統質量、系統阻尼和系統剛度矩陣；{F(t)}為外激勵矩陣。由于阻尼對系統的固有頻率和主振型影響很小，因此可考慮為無阻尼系統，其自由振動方程為

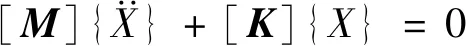
(2)

其特征方程為

(K-ω2M)X=0

(3)

解式(3)可得到系統的第i階固有頻率ωi與第i階的位移Xi。

基于分機殼體(見圖4)，使得PCB約束為四周固定方式，在有限元軟件中進行模態分析。低階模態能量占比大，因此對于本文而言，選取圖5的一階彎曲模態，圖6、圖7的二階彎曲與三階扭轉模態。圖中的條狀圖表示了不同位置的總變形量，前三階所對應最大變形量分別為203.56 mm，183.75 mm，216.16 mm。因此，圖中最大變形區域為振動敏感區域。表1為模態分析所得PCB前三階模態固有頻率。

圖4 分機殼體Fig.4 Extension housing

圖5 一階模態振型Fig.5 The first-order vibration mode

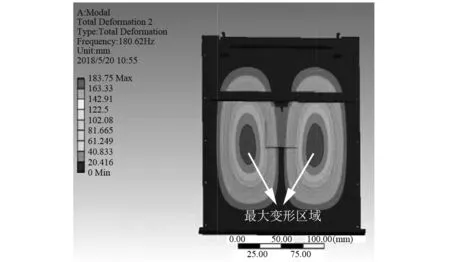
圖6 二階模態振型Fig.6 The second-order vibration mode

圖7 三階模態振型Fig.7 The third-order vibration mode

表1 PCB前三階模態頻率Tab.1 The first three-order modal frequencies of the PCB

通過有限元模態分析，確立了顆粒阻尼安裝的敏感區域，為了更進一步確定阻尼器的安裝位置，將通過諧響應深入分析。

1.3 諧響應分析

通過電路板的諧響應分析可以確定顆粒阻尼器的安裝位置并能得到PCB的峰值頻率。在模態分析的基礎上，對PCB采用模態疊加法進行諧響應分析并求解。求解頻段為模態分析所得電路板固有頻率的最小值與最大值，響應的輸出為加速度頻率曲線。求解條件為：針對PCB的芯片沿X軸方向施加6 mm/s2的加速度(見圖8)，求得節點位置的加速度頻率曲線(見圖9)。

圖8 節點位置Fig.8 Node position

圖9 加速度頻率曲線Fig.9 Acceleration frequency curve

根據以上諧響應分析結果，由加速度頻率曲線可知，電路板上的加速度幅值在頻率為118 Hz，181 Hz，280 Hz時振幅出現了峰值，分別為14.52 m/s2，24.86 m/s2，9.13 m/s2且在頻率為181 Hz時，峰值為最大值。因此，針對PCB的減幅，將重點關注二階模態固有頻率。通過諧響應分析，確定阻尼器的安裝區域為二階模態振型處。

1.4 顆粒阻尼器的設計

顆粒阻尼器是高度的非線型阻尼器，這種阻尼機制隨著顆粒的材料、尺寸、填充率等參數的變化而變化[18-20]，基于多變參數前提下，阻尼器的設計尤為重要。

阻尼器的尺寸越大，能夠填充的顆粒越多，一般阻尼效應也有一定程度的提高，但是PCB的使用面積也會大大減少。因此，在阻尼器形狀的選擇上，考慮有效空間的最大利用率，通過在振動的模態點位置合理的設計阻尼器，并進行阻尼器的優化，力爭做到用最小的質量獲得最優的質量比，從而得到最佳的使用面積。

基于PCB的布局，本文采用正方形阻尼器，其外部尺寸為30×30×8(mm)，阻尼器材質為ZAlZn6Mg鋁合金，采用厚度為1.0 mm的鋁板進行封閉，阻尼器與PCB板之間采用M2十字沉頭螺栓進行連接。為保證阻尼器與PCB之間的固定相連，螺栓底部螺紋可以打上螺紋膠，防止長期使用過程中螺釘的脫落造成阻尼器松動，三維結構如圖10所示。

圖10 阻尼器設計Fig.10 Damper design

2 基于PCB顆粒阻尼器模型的建立

顆粒間通過接觸碰撞由此產生法向力與摩擦的切向力，因此，基于計算的精度及速度，本文在不考慮顆粒間接觸力的疊加上，引入了彈性力與阻尼力，并將法向簡化為線性接觸模型，切向簡化為庫倫摩擦力模型。在PCB上裝有顆粒阻尼器，給出了顆粒間以及顆粒與阻尼壁板間的接觸模型，如圖11所示，其中：kn為顆粒的法向剛度；cn為顆粒的法向阻尼；kt為顆粒切向剛度；ct為顆粒切向阻尼；μ為耦合器，用來確定顆粒的配對關系。

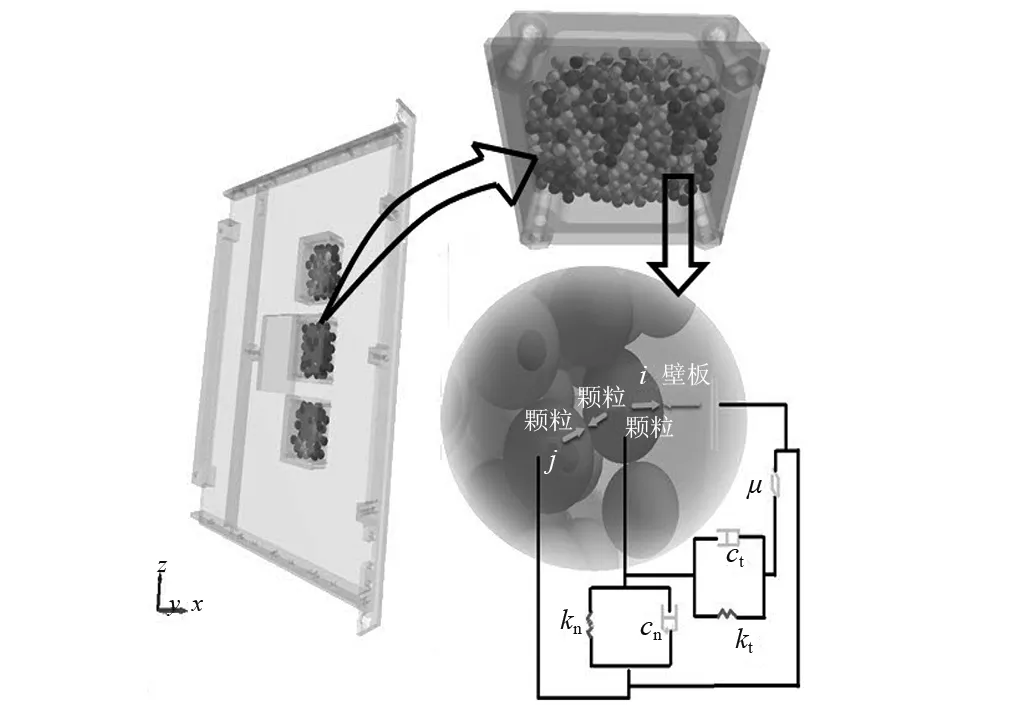
圖11 顆粒的離散元模型Fig.11 Particle discrete element model

PCB在運動過程中，阻尼器中顆粒在某一時刻的運動方程為

(4)

(5)

式中：Fn與Ft為顆粒i，j之間法向接觸力與切向接觸力；pi為顆粒位移向量；g為重力加速度；mi為顆粒的質量；Ii為顆粒慣性矩；φi為顆粒角位移矢量；T為切向產生的扭矩；si為某時刻與顆粒i接觸顆粒數量。法向合力可以表示為

Fn=Fkn+Fcn=-knDn-cnVn

(6)

式中：Dn為顆粒間法向變形量；Vn為粒子間的法向相對速度，可由Hertz接觸理論得出具體值。

用P-P表示顆粒與顆粒，用P-D表示顆粒與阻尼器壁板，則法向彈性系數kn可表示為[21]

(7)

(8)

式中：E為接觸單元的彈性模量；V為泊松比；R為顆粒半徑；m為接觸單元等效質量。

切向合力可以表示為

Ft=Fkt+Fct=-ktDt-ctVt

(9)

式中：Dt為顆粒間切向變形量；Vt為粒子間的切向相對速度。根據Hertz接觸模型，kt與ct可推導為

kt=rkn

(10)

r為比例系數

(11)

(12)

式中：m為接觸單元等效質量；G為接觸單元的切變模量。

顆粒阻尼的耗能包括碰撞耗能和摩擦耗能。當任意兩個顆粒i，j發生碰撞接觸時，碰撞耗能表示為

(13)

式中：e為顆粒的恢復系數；Δv為兩顆粒碰撞前的相對速度。

摩擦力做功決定了摩擦耗能的大小，表示為

ΔEn=μFnΔS

(14)

式中：μ為兩顆粒之間的摩擦因素；ΔS為兩顆粒切向相對位移。

顆粒系統的總體能耗可表示為

E=ΣΔEm+ΣΔEn

(15)

3 PCB阻尼器參數的確定

3.1 顆粒粒徑的選擇

為了使PCB上模態敏感點處的阻尼器具有更高效的減振能力，針對阻尼器的粒徑進行探索優化，圖12為仿真模型。在阻尼器填充空間有限的情況下，優選比重較大的顆粒，因此本文以鎢合金為材料，泊松比為0.28，密度為1.935×104kg/m3，彈性模量為3.24×1011Pa。

3.1.1 顆粒的粗優化

顆粒過小，則顆粒越接近于流體的形態，失去了固態的特性，如果顆粒過大，顆粒間隙過大，碰撞次數較少。本文粗選顆粒粒徑為1 mm，1.5 mm，2 mm，2.5 mm，3 mm填充率85%為例。在離散元軟件中導入模型，添加顆粒的生成界面，給予模型為X軸的振動5 mm，頻率設置為181 Hz的正弦運動。基于仿真效率與速度，仿真時間設置為1 s。

圖12 顆粒模型樣圖Fig.12 Particle model figure

如圖13通過離散元方法分別統計不同顆粒尺寸不同時刻的耗能效果。表2為1 s內顆粒總能量耗散情況。經過粗選的顆粒尺寸，從圖表中易得2 mm的鎢合金顆粒耗散能量最大。但隨著顆粒尺寸的增大能耗有所下降，后文將通過試驗進行進一步探究。

圖13 不同時刻的耗能圖Fig.13 Different time diagram of energy loss

表2 顆粒的總能耗Tab.2 Total energy loss of particles

3.1.2 顆粒的細優化

基于粗選的顆粒尺寸，2 mm顆粒的耗能效果顯著。為此，以2 mm尺寸為界，進一步探索細微尺寸的能耗效果。細選粒徑為1.8 mm，1.9 mm，2 mm，2.1 mm，2.2 mm，填充率為85%，參數設置不變。如圖14通過離散元方法分別統計細微顆粒尺寸的耗能效果，能得到不同時刻的能量耗散情況。表3則為1 s內的顆粒總能量耗散情況。經過細選的顆粒尺寸，從圖表中易得1.9 mm的鎢顆粒耗散能量最大。因此，細選1.9 mm的鎢顆粒具有最佳減振效果。

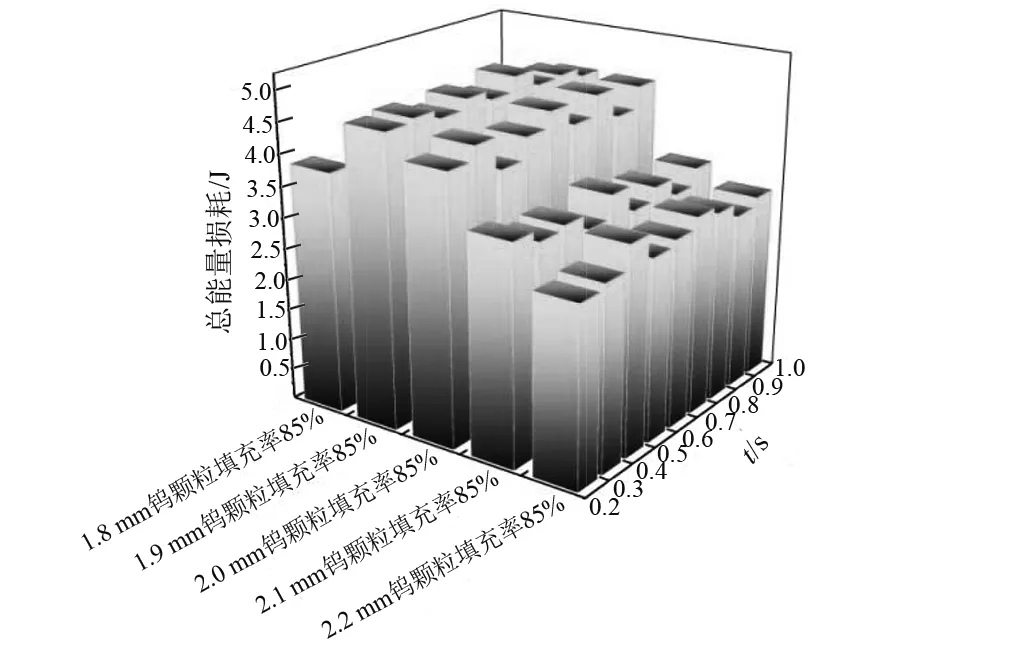
圖14 不同時刻顆粒的耗能圖Fig.14 Different time diagram of energy loss

表3 顆粒的總能耗Tab.3 Total energy loss of particles

3.2 顆粒填充率的優化

在離散元軟件中導入模型，設置相同的參數與運動情況。阻尼顆粒需要保證在有限空間內能夠有一定的運動行程，這樣才能增大顆粒與顆粒之間摩擦與碰撞的機會，如圖15所示，本文以填充率為75%，80%，85%，90%，95%為方案，1.9 mm鎢合金材料顆粒為例，進行仿真計算。

圖15 填充率模型樣圖Fig.15 Fill rate model figure

不同深淺的顆粒表示了不同的運動速度，顏色越深，顆粒速度越大。如圖16所示，通過離散元方法分別統計不同填充率顆粒阻尼器不同時刻的能量損耗。表4則為不同填充率下顆粒的總能耗。根據能量損失圖表易得隨著顆粒填充率的不斷提高，顆粒阻尼效果越明顯，90%填充率的鎢合金顆粒耗散能量最大。但是當顆粒填充率到達95%時，耗能情況有顯著的下降。

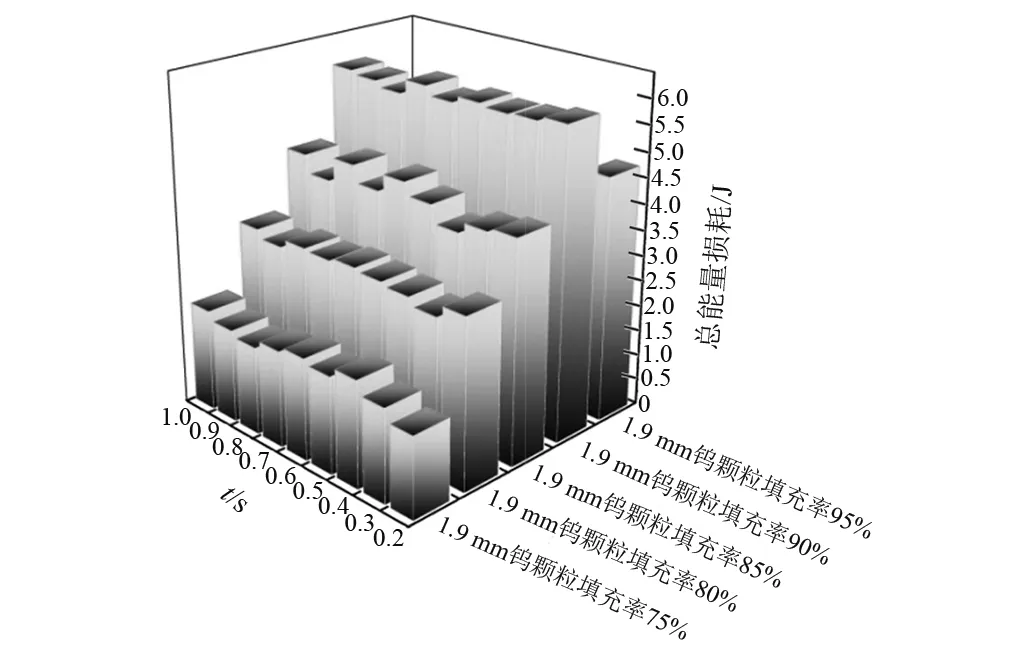
圖16 不同時刻耗能圖Fig.16 Different time diagram of energy loss

表4 顆粒的總能耗Tab.4 Total energy loss of particles

3.3 顆粒尺寸與填充率的關聯

上文對顆粒尺寸的優化和顆粒填充率的優化是分開進行的，為了驗證二者之間的關聯性，尋求最佳的適配值，做出如下仿真。仿真參數與過程與前文相同，顆粒尺寸以1.5 mm，1.8 mm，1.9 mm，2 mm，2.5 mm，填充率以80%，85%，90%，95%為方案。不同粒徑對應不同填充率的耗能情況，如圖17所示。

不同的粒徑有最佳的填充率，1.5 mm粒徑最佳填充率為85%，1.8 mm，1.9 mm，2 mm，2.5 mm最佳填充率為90%。當選擇1.9 mm粒徑，填充率為90%時，它的總能耗值是最高的。因此，對于本文而言，當顆粒直徑為1.9 mm時，其所對應的最佳適配填充率為90%。

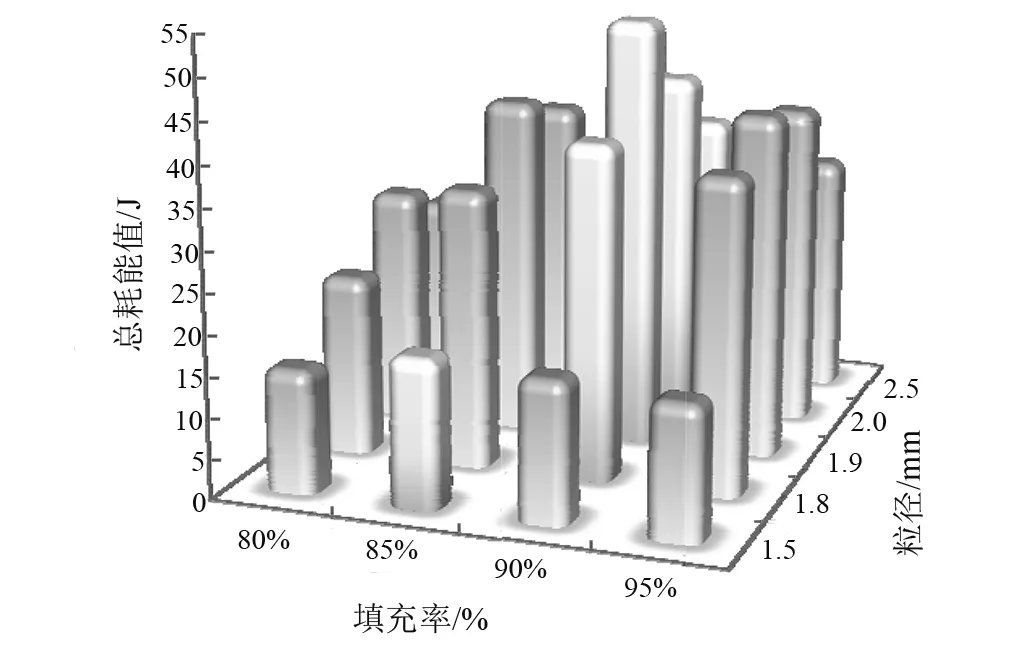
圖17 總耗能Fig.17 Total energy loss

3.4 仿真結論

基于鎢顆粒的離散元分析，分別從顆粒的尺寸大小、填充率以及二者的關聯性進行仿真優化。驗證了阻尼器參數在鎢顆粒粒徑大小為1.9 mm，填充率為90%時能使PCB達到最優化的減振效率，確定最優阻尼的配置設計方案為下一步電路的設計奠定基礎。

4 試驗驗證

針對北京華航無線電測量研究所某PCB，設計制造樣機試驗用殼體、試驗用阻尼器外殼，選擇測點，進行顆粒粒徑、填充率的試驗驗證。

PCB結構尺寸為192×179×2(mm)，PCB材料為FR-4，重量為226×10-3kg，用加速度傳感器實測PCB在正弦振動時的均方根值，規定PCB的整體方位與測點如圖18(a)所示。由于PCB上已經布滿了現有電路，增加阻尼器不能對電路造成破環，為此，增加阻尼器位置為無電子線路的空白PCB部分。

PCB的外層殼體如圖18(b)所示，圖上所示的三個方位與PCB的方位相匹配，從而實現完美的對接。阻尼器采用厚度為1.0 mm的鋁板進行封閉，重量達到15×10-3kg(包括緊固件)，加工實物圖如圖19所示。在振動臺上(見圖20)，長箭頭的表示振動臺的主振方向，平行于長箭頭的短箭頭為PCB的X方向，圖示為PCB主振X的方向。

基于動力學分析，對PCB的減振，將重點關注二階模態固有頻率，為了達到消減峰值的目的，阻尼器將安裝于二階模態振型處。

圖18 電路板與分機殼體Fig.18 Circuit board and extension housing

圖19 阻尼器實物圖Fig.19 Damper physical figure

圖20 主振X方向Fig.20 The main vibration direction of X

4.1 顆粒粒徑的驗證

PCB通過夾具固定在振動臺上，實測樣機在正弦振動下的響應，設置參數為沿主振X方向振動5 mm，設置頻率為181 Hz。探索不同顆粒直徑對減振效果的影響，以1 mm，1.5 mm，1.9 mm，2.5 mm，3 mm顆粒尺寸，填充率為85%為例，采用圖21的布置方案，顆粒尺寸如圖22所示，所得加速度均方根值如表5所示。

圖21 排布方案Fig.21 Arrangement plan

圖22 顆粒尺寸Fig.22 Particle size

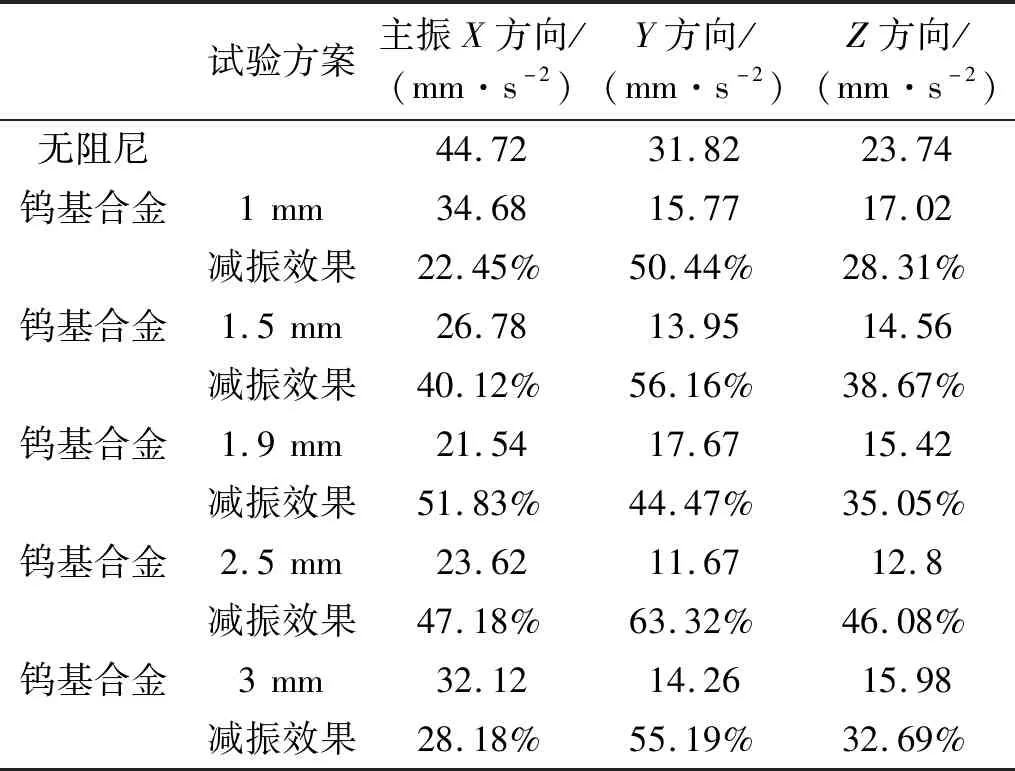
表5 測點加速度均方根值Tab.5 Measured point acceleration RMS

由表5的數據可明顯得出，在顆粒的主振方向上，直徑為1.9 mm的鎢顆粒減振效果優于其他粒徑的鎢顆粒。減振效果在主振方向上可以達到50%以上，將試驗結果與仿真結論進行對比。如圖23所示，兩條曲線具有高度的相似性，均證明了對于本文的PCB，1.9 mm尺寸的鎢顆粒具有較好的減振效果。

圖23 試驗與仿真對比圖Fig.23 Comparison of test and simulation

4.2 顆粒填充率的驗證

PCB通過夾具固定在振動臺上，實測樣機在正弦振動下的響應。探索不同填充率對減振效果的影響，以1.9 mm鎢顆粒，75%，80%，85%，90%，95%填充率為例，采用圖21的布置方案，所測得加速度均方根值如表6所示。

表6 測點加速度均方根值Tab.6 Measured point acceleration RMS

從顆粒的填充率上來看，90%填充率的鎢顆粒減振效果優于其他填充率的鎢顆粒。試驗中減振效果在主振方向上可以達到50%以上，效果十分明顯。將試驗結果與仿真結論進行對比，如圖24均證明了對于本文的PCB，90%鎢顆粒填充率具有較好的減振效果。

圖24 試驗與仿真對比圖Fig.24 Comparison of test and simulation

4.3 阻尼器安裝位置的驗證

基于有限元動力學分析，在二階模態固有頻率為181 Hz時，振動峰值達到最大點。對于本文的PCB，基于原有電路的設計，在接線與元器件排布位置的基礎上，只留下圖25中非敏感位置。

針對電路板進行掃頻分析，掃頻范圍為0～330 Hz，通過頻譜圖驗證PCB上敏感區域與非敏感區域加阻尼器的減振效果。如圖26所示，圖26(a)為非敏感區域電路板安裝阻尼器的方案，圖26(b)為敏感區域電路板安裝阻尼器的方案。

對比試驗結果，通過頻域曲線進行分析，如圖27所示，在非敏感區域安裝顆粒阻尼器后，總有效值從40.75 mm/s2降到了39.33 mm/s2，沒有明顯的減振效果。在敏感區域加上阻尼器后，總有效值從40.75 mm/s2降到了20.50 mm/s2，降幅在主振方向上可以達到50%。二階頻率的峰值從27.35 mm/s2降到了15.80 mm/s2，達到很好的降峰效果，整體減振效果十分顯著。

圖25 電路板的非敏感區域Fig.25 Non-sensitive area of the circuit board

圖26 阻尼器安裝位置Fig.26 Damper installation position

圖27 頻譜圖Fig.27 Spectrogram

5 結 論

(1)針對目前PCB結構及振動條件，在阻尼器形狀的選擇上，需考慮有效空間的最大利用率，并通過敏感點的位置合理的設計阻尼器。在顆粒阻尼參數的選擇上，采用鎢基合金顆粒，理論直徑為1.9 mm，填充率為90%時，電路板達到最優化的減振效果。

(2)基于動力學特性分析尋求模態敏感區域，通過阻尼器安裝位置的選擇，驗證在敏感區域安裝阻尼器能使PCB在主振方向上達到50%減振效率。

(3)本文提出PCB的動力學分析與電路聯合設計方法，改善了PCB的抗振特性。基于布線合理性、布通率與電氣性，調整元器件位置與接線布置使得在電路板模態敏感點區域留出余裕。在非敏感區域設計電路，在敏感區域安裝顆粒阻尼器。針對顆粒阻尼器模型設計與構建，完成整個電路體系的設計，大大提升了導彈電子設備的穩定性。