力的要素變化對題目的影響

李奮山

摘?要：在力學問題中，有一種動態平衡問題，即由于一個物理量的變化，引起其他物理量緩慢的變化，因為具有一定的綜合性，成為高考試題的熱點選題。由于其解決方法具有一定的技巧性，所以也是學生學習中的一個難點。解決動態平衡問題的方法主要有解析法、圖解法和相似三角形法，不同方法適合不同條件的題目，學生總是分不清楚，下面主要以題目已知條件的多少為線索介紹相應的解題方法。

關鍵詞：動態平衡;力的要素;圖解法;相似三角形法

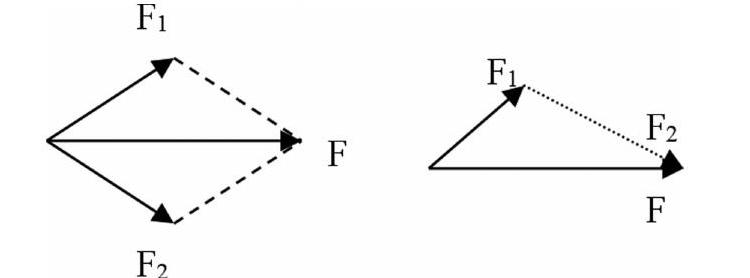
我們常見的問題主要是三個共點力作用下的平衡問題（超過三個力可以通過合成的方法等效為三個力的問題），每個力都有大小、方向、作用點三個要素，三個力應有九個要素，但由于是共點力，所以作用點相同，這樣三個力我們只關注大小、方向共六個要素。

一、若六個要素中已知四個（或四個以上）要素，其余兩個要素是確定的

如已知兩個分力的大小和方向，合力的大小和方向完全是確定的。

如已知合力的大小方向、一個分力的大小方向，根據三角形法則，另一個分力是確定的。

二、若六個要素中已知三個要素，可以用解析法或圖解法判斷其余三個要素的變化

例1.如圖所示，把球夾在豎直墻AC和木板BC之間，不計摩擦，墻對球的彈力為N?1?，板對球的彈力為N?2?。在將板BC逐漸放至水平的過程中，關于彈力變化說法正確的是（?）。

A.N?1?和N?2?都增大?B.N?1?和N?2?都減小

C.N?1?增大，N?2?減小?D.N?1?減小，N?2?增大

解析：本題中小球重力的大小和方向，墻對小球的支持力的方向三個要素是確定的，在這種條件下，可以用解析法判斷變化情況。

以小球為研究對象，進行受力分析：小球受到重力mg，墻對小球的支持力N?1?和板對球的支持力N?2?。設板與墻間的夾角為θ，在力矢量三角形中，

mgN?1=?tan?θ?得：?N?1=mg?tan?θ

mgN?2=?sin?θ?得：?N?2=mg?sin?θ

將板BC逐漸放至水平的過程中，θ增大，?tan?θ?增大，所以N?1?減小，?sin?θ?增大，N?2?減小。

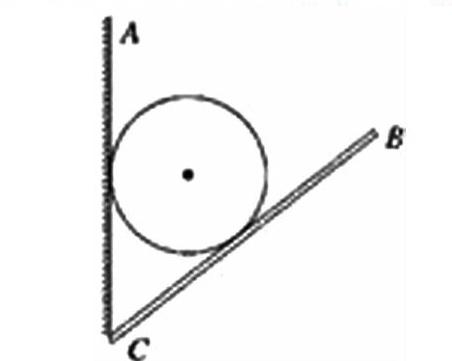
例2.如圖所示，將一光滑小球放在固定斜面和豎直擋板之間，若他將擋板逆時針緩慢轉到水平位置，在這一過程中，小球保持靜止，斜面和擋板對小球的彈力大小F?1?、F?2?的變化情況正確的是（?）。

A.F?1?逐漸變大?B.F?1?先變小后變大

C.F?2?先變小后變大?D.F?2?逐漸變小

解析：本題中小球重力的大小和方向，斜面對小球的支持力的方向三個要素是確定的，由于板與斜面的夾角變化大于90?0?，正弦、正切的單調性發生變化，解析法不再適合，可用圖解法判斷。

以小球為研究對象，進行受力分析：小球受到重力mg、斜面對小球的彈力F?1?和擋板對小球的彈力F?2?，三力平衡，任意兩個力的合力與第三個力等大反向，作出F?1?，F?2?的合力，這個合力與重力mg等大反向，當擋板繞O點逆時針緩慢地轉向水平位置的過程中，F?2?相應的逆時針旋轉，做出力的平行四邊形，可以看到，F?1?逐漸變小，F?2?先變小，后變大。

三、若六個要素中已知兩個要素，可以相似三角形法判斷其余四個要素的變化

例3.固定在水平地面上半徑為R的光滑半球，球心O的正上方固定一大小可忽略不計的定滑輪，細線一端拴一半徑為r的小球，另一端繞過定滑輪.今將小球從下圖所示位置A緩慢地拉至頂點B，在小球到達B點前的過程中小球對半球的壓力N?/?，細線的拉力F的大小變化情況正確的是（?）。

A.N?/?變大、F變大?B.N?/?變小、F變大

C.N?/?不變、F變小?D.N?/?變大、F變小

解析：本題只有小球重力的大小和方向兩個要素是確定的，只能用相似三角形法判斷。

以小球為研究對象，進行受力分析，如圖所示，小球受到細線的拉力F、半球對小球的支持力N和重力G的作用，由于小球從圖中位置被緩慢拉至頂點B，在此過程中小球處于動態平衡狀態，小球所受合力為零，拉力F和支持力N的合力與重力等大反向。由圖可以看出，幾何三角形AOC與由G、N、F構成的三角形相似，有以下比例關系：

NR+r=FL=GR+h

上式中，R、r、h、G均不變，當小球向上運動時，繩長L減小，N不變，F變小，根據牛頓第三定律，小球對半球的壓力大小N?/?=N，故N?/?不變。

綜上所述：選項C正確。

通過以上分析可以看出，如果有三個要素確定，判斷其余三個的變化情形時，可以用解析法或圖解法（圖解法比解析法的使用范圍更廣）;如果只有兩個要素確定，判斷其余四個的變化情形時，可以用相似三角形法。通過對已知條件的分析，找出合適的解題方法，以上難點也就迎刃而解了。