移動的串聯多Agent系統干擾影響研究

江 帆，張晨潔

(1.江蘇聯合職業技術學院 蘇州工業園區分院， 江蘇 蘇州 215123；2.長春理工大學 電子信息工程學院， 長春 130022)

無人車隊控制理論的研究不僅具有實際意義還具有重要的工程應用價值，由具有一般特性的交通流模型分析出其基本規律，通過數值模擬以及公式推導得出模擬參數取值的范圍，通過實例顯示了擾動的傳播規律。

交通流從自由流到擁擠流的演變是一個強非線性的復雜過程，具有多種不同的表現形式。在密度和流量都遠未達到飽和的條件下，一定的擾動也會引發擁堵，這不同于傳統意義下道路瓶頸產生的堵塞，其中每輛車在列隊中都有相對于前一輛車的位置誤差。在這樣的系統中，一個小的擾動作用于一個成員可以傳播到下游，并造成車輛之間的大間距誤差。

許多科學家對這個問題提出了許多有價值的研究， H.W.Bode[1]給出的經典積分公式對反饋控制系統的性能提出了基本的限制。對于離散時間單輸入單輸出(SISO)線性定常系統，假設開環系統是合理的，且嚴格適用。無論采用何種線性定常(LTI)控制器來穩定系統，系統對外界干擾的靈敏度在所有頻率下都不能變小。對于更一般的控制設置，包括多維、非線性和時變系統，也得出了類似的性能限制。但是，仍然缺少將Bode的積分公式推廣到分布式控制的方法。一般情況下，分布式控制問題是NP-hard[2]，因此在此設置中等效Bode的積分公式尤為重要，因為它可以為評價實際控制設計提供有用的工具。

在此考慮的是一個一維無人車隊控制問題，目標是在保持一定編隊[3]，將一列車輛從一個點移動到另一個點。領先車輛的目標是遵循特定的參考軌跡，而后面的車輛的目標是相對于它們的前一輛車保持一個恒定的間距。早期對這個控制問題的興趣是由自動化高速公路系統(AHS)等應用提出的，對這些應用來說，集中控制是不切實際的。它們的控制律不同(例如，線性與非線性)，更重要的是，它們的信息流結構[4]也不同。已知存在隨著車輛數量的增加而導致一串不穩定的信息流結構，因為作用在排長上的小擾動在沿隊列傳播時會被放大。我們關注的是信息流結構[5]的“先有后有”，其中每輛車只訪問前一個車的輸出，并使用間距誤差作為控制器的輸入。在這種情況下，我們的目標是研究連續車輛之間的間距誤差對隨機干擾影響領導者的測量的敏感性。

綜上所述，本文的貢獻是研究了無人車隊控制系統的性能限制問題。給出了一個與控制器無關的對數靈敏度函數積分下界，表明隨機擾動對前導的影響不能沿著列隊任意衰減。這個邊界適用于一類嚴格包含LTI控制器的非線性控制器[6]。討論下界的封閉性，并給出了數值結果，說明下界對實際控制器設計的重要意義。這一結果的證明技術依賴于信息論工具，這些工具可用于推導其他分布式控制問題的相似邊界。

1 靈敏度函數積分下界模型

1.1 無人車隊系統的基本模型

無人車隊模型對預測交通系統有著重要的實際意義，擁堵在交通中是一個重要現象，當交通系統中存在擾動時會造成嚴重的交通堵塞。因此，建立無人車隊控制系統的模型是為了解決其動態穩定問題，需要明確哪些狀態對擾動傳播會產生反應。對無人車隊控制系統[7]的擾動傳播分析，考慮由M+1個控制單元組成的一串相互連接和動態耦合的單輸入單輸出(SISO)系統，如圖1所示。

圖1 兩個子系統組成的無人車隊(M=1)

圖1中，P表示每輛車輛的控制系統單元，K表示相應的控制器。

H.W.Bode在文獻[1]中提出的經典積分公式為

(1)

式中：S(ejw)為輸入輸出靈敏度函數；λi為開環系統的極點，假設開環系統是合理的，且嚴格適用。

第i個控制單元(0≤i≤M)的動力學模為

xi(k)=AiXi(k-1)+Biui(k-1)

yi(k)=Cixi(k)

(2)

其中：xi(k)∈Rni為系統狀態，yi(k)∈R為系統輸出，ui(k)∈R為控制輸入。例如，輸出表示車輛沿直線的位置。領頭的車輛的目標是跟隨一個參考命令信號r0(k)，其輸出y0(k)假設被反饋回路中的隨機擾動d(k)擾動。對于一個給定的常數δ，每個跟隨的車輛i(1≤i≤M)旨在調節其輸出yi(k)滿足yi-1(k)-yi(k)=δ，時間步長為k。

連續車輛的間距誤差：

e0(k)=r0(k)+d(k)-y0(k)

ei(k)=yi-1(k)-yi(k)-δ,1≤i≤M

(3)

在k時刻，第i個控制器接入ei(0),ei(1),…,ei(k)由式(4)產生因果控制信號：

(4)

1.2 積分下界模型的基本假設

假設在式(4)中可能的非線性控制映射ui,k使得描述閉環動力學的隨機過程具有定義良好的連續聯合概率密度函數[8-9]，并且是漸近平穩過程。此外，具體技術假設如下：

ui,k(ei(0),…,ei(k-1),x)

(5)

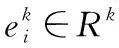
(6)

為了處理擾動過程的隨機性，采用了Martins等[9]的方法，并采用了漸近平穩隨機過程的靈敏度概念。如果隨機過程的任意n維分布不隨時間起點變化[10]，即當時間平移時，其任意n維概率密度不變，則為漸進平穩隨機過程。

靈敏度函數Sx,y(w)的兩個漸近平穩隨機過程x和y與功率譜密度φx(ω)和φy(ω)被定義為式(7)所示：

(7)

參考的文獻[9]討論的主要是靈敏度函數屬性Sx,y(ω)及其與經典的輸入-輸出靈敏度函數的關系。

本文的目的是給出間距誤差過程ei,0≤i≤M，對d的對數靈敏度積分的下界：

(8)

2) 所有的閉環子系統都是穩定的。

3) 所有的控制單元都是嚴格合適的和可觀測的。

4) 單元模塊的初始條件是具有有限微分熵的隨機變量，xi-1(0)→xi(0)→xi+1(0)形成馬爾可夫鏈。此外，x0(0),…,xM(0)獨立于擾動過程d。

5) 擾動過程d為漸近平穩高斯過程。

在本文中，用vi∈N表示第i個單元的相對程度，即，在傳遞函數ui到yi的分子和分母上的主導系數的比值。用ti表示到單元i的相對程度之和，如式(9)所示：

ti=v0+v1+…+vi

(9)

2 初步結果

2.1 引理的列舉及證明

為證明所提出的主要定理需要以下引理：

引理1讓假設(2)～假設(4)成立。

(10)

引理1的證明與文獻[9]中的引理4.1中的證明步驟相同。文獻[9]中的引理1和引理4.1的主要區別在于對添加擾動的假設。而在考慮的系統模型中，在采取控制動作之前，先將外部干擾yi-1添加到系統輸出中(圖1)，可視為影響輸出yi的測量噪聲，文獻[9]中的問題設置假設擾動過程被加入到控制輸入中，可以認為是直接影響裝置的系統噪聲。

引理2讓假設(1)～假設(4)成立。對于每個0≤i≤M和k足夠大。

Ui,k+h(d(k-ti)|dk-ti-1)

(11)

其中

(12)

式(8)中的界限可以解釋如下。由于微分熵[12]的可標度性和假設(1)，當擾動d在交通流隊列中從第j個車輛傳播到第j-1時，條件微分熵h(d(k-ti)|dk-ti-1)的可標度為式(13)。

(13)

其中第一項只依賴于第j個線性系統的動力學而第二項依賴于第j個控制器它將ej映射到uj。因此，式(11)通過迭代累加到第i個控制器的所有比例因子式(13)得到。

有一些重要的控制器類可以用式(12)一個緊湊的閉合達式來表示。例如，考慮這樣一種特殊情況：根據以下穩定的離散時間LTI動態系統遞歸地形成控制輸入ui。

(14)

其中zi是已知初始條件z0的控制器內部狀態。從式(14)可以看出，zi(k)是ei(0),…,ei(k-1)的一個線性函數：

(15)

對于每一時刻的k，在這種情況下(11)的右邊就等于式(16)。

(16)

引理3讓假設(1)～假設(4)成立。然后，對于每個0≤i≤M都有：

(17)

其中

(18)

注意式(17)的右邊由3項組成。前兩項表示交通流中第i個控制器之前的幾個所造成的縮放效果。第3項量化了從初始條件xi(0)到第i個跟隨車輛的控制器輸入的信息流。

2.2 無人車隊控制系統的限定定理

將給出的3個引理與最大熵定理[13]相結合，即得到擾動傳播性能的下界如式(19)。

定理1當假設(1)～假設(5)成立時，對于每一個0≤i≤M。

(19)

下面的推論提供了定理1的界是封閉的條件。

3 數值驗證

3.1 定理的評估與分析

評估在文獻[10]中研究的特定設置中間距誤差的靈敏度函數和時間響應。考慮一個由五輛車組成的隊列，即M=4，其中每輛車建模為具有一階執行器動力學的雙積分器[11]，其動力學描述為連續時間開環傳遞函數：

(20)

在某列車輛中第一個控制器的目標是跟蹤低頻參考信號。

(21)

此處，r0(t)模擬了這樣一個場景：前導車輛從靜止加速到12 m/s，加速度為2 m /s2，然后保持恒定速度。將作用于前導的擾動過程d建模為一個標準的高斯白噪聲過程。下面車輛的初始位置設為(-0.1,0.1)均勻分布。

假設每輛車使用相同的LTI控制器。具體地說，由于控制器的不同導致了車輛行進過程影響中間距誤差的因素不同，為研究間距誤差的靈敏度函數和時間響應則需比較兩個控制器的性能，其特征是連續的時間傳遞函數，K1、K2分別為控制器1和控制器2：

(22)

分別計算定理1中給出的對數靈敏度函數的下界，很容易看出K2對應的下界小于K1對應的下界(因為K2中的控制增益較小)。因此，根據定理1，我們期望K2具有比K1更好的干擾抑制性能。

3.2 仿真結果驗證

通過上述分析，對定理1進行數值驗證。先對兩個控制器的靈敏度進行對比，由增益隨頻率的變化來反映控制器的靈敏度，得出抗干擾性能的強弱。其次又對有無噪聲條件下控制器的間距誤差性能進行對比分析，通過仿真圖得出結論。

上述系統以4 Hz的采樣速率離散化。圖2(a)和圖2(b)分別為K1(控制器1)和K2(控制器2)的靈敏度函數和互補靈敏度函數增益的變化，需要注意的是，在文獻[10]所示的在所有頻率下都不可能實現干擾衰減。同時，從圖2(a)中靈敏度曲線可以看出，K2在低頻下性能較差，即在低頻時，控制器2對應的靈敏度大于控制器1對應的靈敏度。然而，從圖中還可以看出，虛線下的面積小于實線下的面積，反映出K2總體上具有更好的抗擾性能，驗證了定理1的有效性。K1和K2之間的性能差異表明跟蹤性能和噪聲抑制之間存在張力。

圖2 控制器K1和K2的誤差傳播性能

圖3(a)為可視化這種張力的方法[14]，該圖展示了假設d=0隊列中任意兩個連續車輛之間的間距誤差，即領頭的車輛沒有受到干擾。在無噪聲干擾的這種情況下，可以看到K2比K1有更差的跟蹤性能(更大的間距誤差)，因為r0(t)的功率含量在低頻段。然而，當干擾d為高斯白噪聲過程時，如圖3(b)所示，控制器K1的性能迅速下降，且比K2更差。在實際應用中，由于測量噪聲等影響，反饋回路中會產生噪聲。這里提出的結果與這種情況有關。

圖3 間距誤差

4 結論

本文研究了具有信息流結構的無人車隊控制系統擾動傳播問題。利用信息論技術，推導了隨機擾動作用于車隊的跟蹤誤差對數靈敏度函數積分的下界。這個邊界適用于一類非線性的控制器。通過數值算例判斷了下界的封閉性并驗證了理論結果的正確性。

實驗結果表明：本文所描述的為一般分布式控制系統邊界。未來的工作要將所提出的結果擴展到MIMO系統，因此，未來研究的另一個方向是對不同信息流結構的擴展。