鋁合金疲勞裂紋分布式光纖監測與擴展預測方法
鄭丁午,曾 捷,夏裕斌,顧 欣,于惠勇
(1.南京航空航天大學 機械結構力學及控制國家重點實驗室,江蘇 南京 210016;2.上海航空測控技術研究所 故障診斷與健康管理技術航空科技重點實驗室,上海 201601)
0 引言
在航空航天器服役過程中,由于疲勞載荷,結構老化,各種環境腐蝕及沖擊等影響,使得結構易產生累積損傷甚至失效。其中疲勞裂紋失效最顯著,多數結構損壞都是在外界復雜環境作用下結構出現微裂紋,然后擴展最后完全失去作用[1-2]。因此,開展針對金屬結構疲勞裂紋的擴展監測研究,具有重要理論意義和工程實踐價值。
光纖Bragg光柵(FBG)傳感器具有質量輕,芯徑細,抗電磁干擾及便于分布式監測等優點,在結構健康監測領域已受廣泛關注[3]。Andrea Bernasconi等[4]利用光纖光柵傳感器,開展針對復合物粘接接頭裂紋的監測。Bao P等[5]基于FBG傳感陣列提出頻譜互相關分析(SCCA)和損傷特征因子對疲勞裂紋進行在線實時監測。Zhang Q等[6]利用FBG傳感器,基于希爾伯特黃變換(HHT)法對混凝土拱裂紋進行監測。Yang D等[7]采用光纖POF傳感器實現針對疲勞載荷下裂紋萌生和傳播特性的監測。Ayad Kakei等[8]利用FBG傳感器反射光譜和紅外攝像機記錄的熱彈性響應,檢測玻璃纖維增強復合材料分層裂紋尖端擴展。黃紅梅[9]針對金屬修補結構所受非均勻應變,利用FBG重構反射光譜監測疲勞裂紋擴展。
本文針對單邊缺口鋁合金試件提出基于光纖FBG傳感器的疲勞裂紋及其擴展監測法。借助數值模擬與試驗方法建立了FBG傳感器中心波長偏移量ΔλB與裂紋長度關系預測模型,實現針對疲勞裂紋位置與長度的有效辨識。
1 基本原理
根據光纖耦合模理論,FBG反射光中心波長取決于光柵周期Λ和纖芯有效折射率neff,寬帶光在光纖光柵中傳播時,滿足Bragg條件的光信號被反射,FBG諧振方程[10]為
λB=2neffΛ
(1)
式中λB為光纖光柵反射光中心波長。FBG應變感知機理如圖1所示。

圖1 光纖布喇格光柵應變傳感機理
由式(1)可看出,任何能改變neff或Λ的物理量都可以引起光柵λB變化,而通常引起λB發生偏移最直接的外界物理量是應變和溫度。若忽略外界環境溫度變化,則ΔλB和FBG軸向應變Δε的關系為
ΔλB/λB=(1-Pe)Δε
(2)
式中Pe為光纖光柵有效彈光系數。式(2)表明,λB與其所受應變呈現良好線性關系。因此,應變監測可利用ΔλB來表征。
2 疲勞裂紋擴展有限元仿真分析
2.1 試件材料與尺寸
試驗試件選用尺寸為240 mm×200 mm×15 mm的鋁合金材料,其彈性模量為70 GPa,泊松比為0.33。在試件左端預制一個長37 mm的缺口,用以控制裂紋沿著缺口方向擴展。試件結構尺寸如圖2所示。
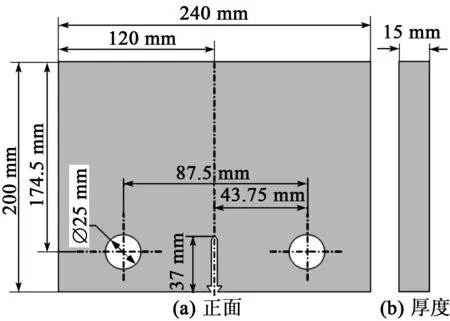
圖2 單邊缺口鋁合金試件模型
2.2 試件有限元模型與網格劃分
利用Abaqus有限元仿真軟件建立疲勞裂紋擴展有限元仿真模型,如圖3所示。針對裂紋尖端進行奇異單元設計,以保證裂紋尖端應力、應變的奇異性[11-12]。為平衡計算精度和速度,對裂尖采用C3D15楔形單元和C3D20二次完全積分六面體單元,其余區域采用C3D8R縮減積分六面體單元。裂尖定義種子以sweep進行單元劃分,FBG粘貼位置區域定義網格大小為0.5 mm,其余區域定義網格大小為5 mm。
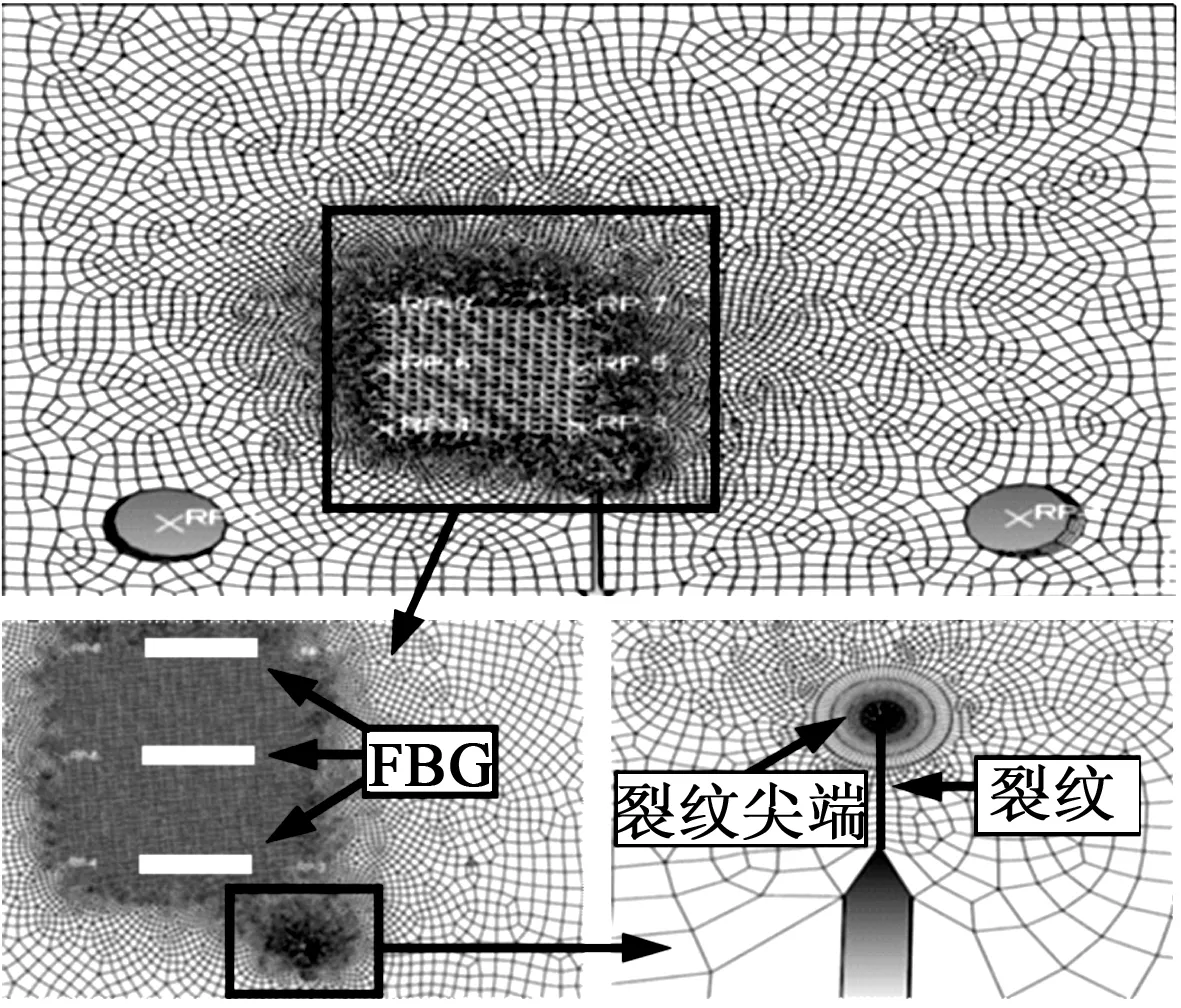
圖3 含預制裂紋鋁合金有限元模型與網格劃分
2.3 傳感器布局
由于應力集中效應,裂尖會產生較大應力應變,因此,FBG傳感器需要布置在應變幅值梯度較大區域[13-14]。這里定義試件兩圓孔中心連線與裂紋擴展方向的交點為裂紋起點。
數值仿真中,沿裂紋擴展方向假定在距離缺口20 mm、40 mm和60 mm處依次布置FBG1、FBG2和FBG3 3個應變傳感器,即距離裂紋起點依次為32.5 mm、52.5 mm及72.5 mm處。根據裂紋擴展路徑周邊應變場分布特征,優化配置FBG應變傳感器與裂紋擴展路徑垂直間距。裂尖附近FBG傳感器優化布置區域,如圖4所示。
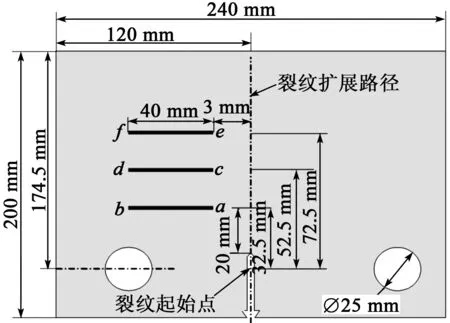
圖4 FBG傳感器優化配置區域
建立不同裂紋長度鋁合金有限元模型,數值仿真得到不同裂紋擴展長度下,ab、cd及ef沿線應變分布特征(見圖4)。圖5為ab、cd及ef沿線在不同裂紋擴展長度下的應變分布特征曲線。
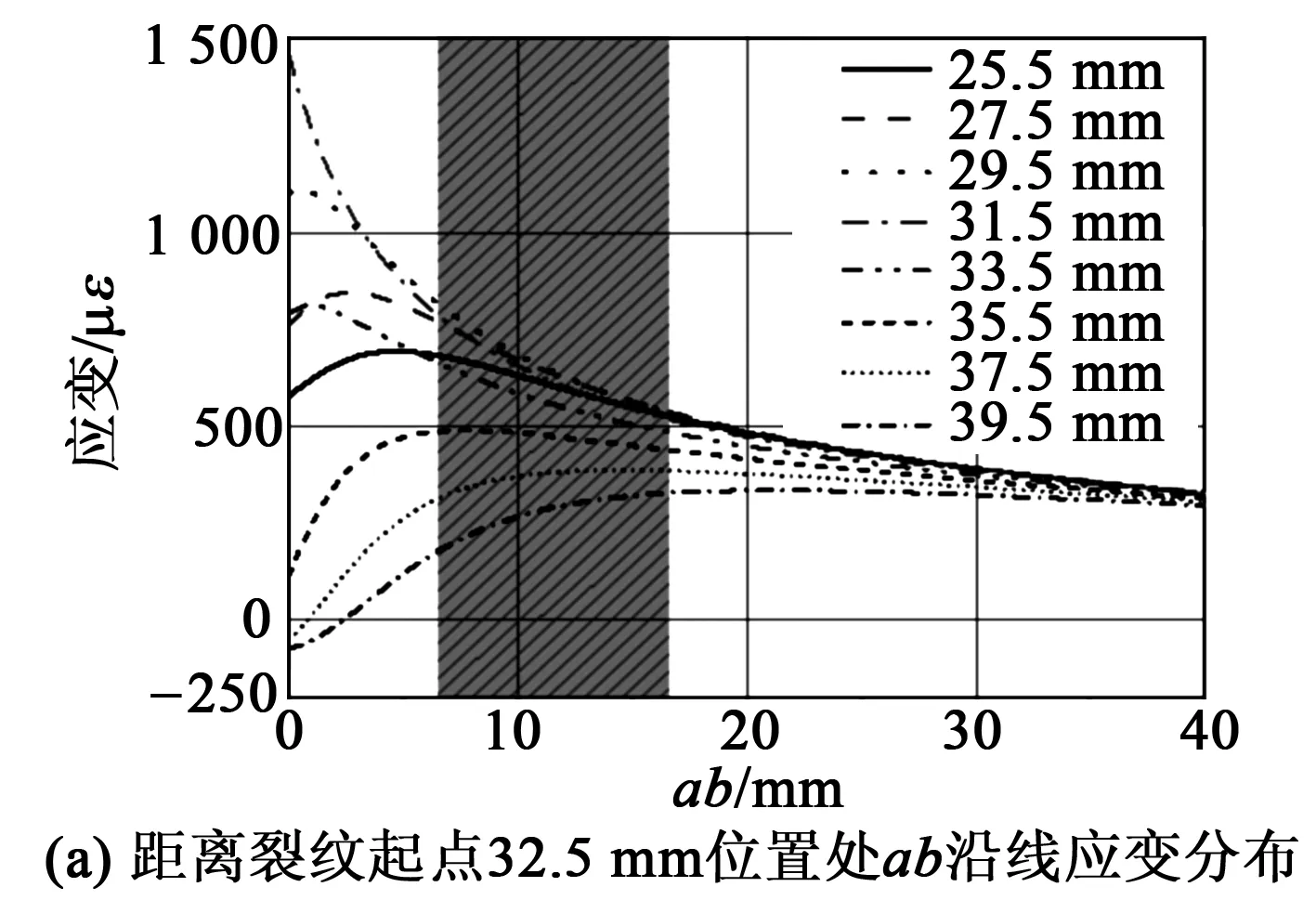
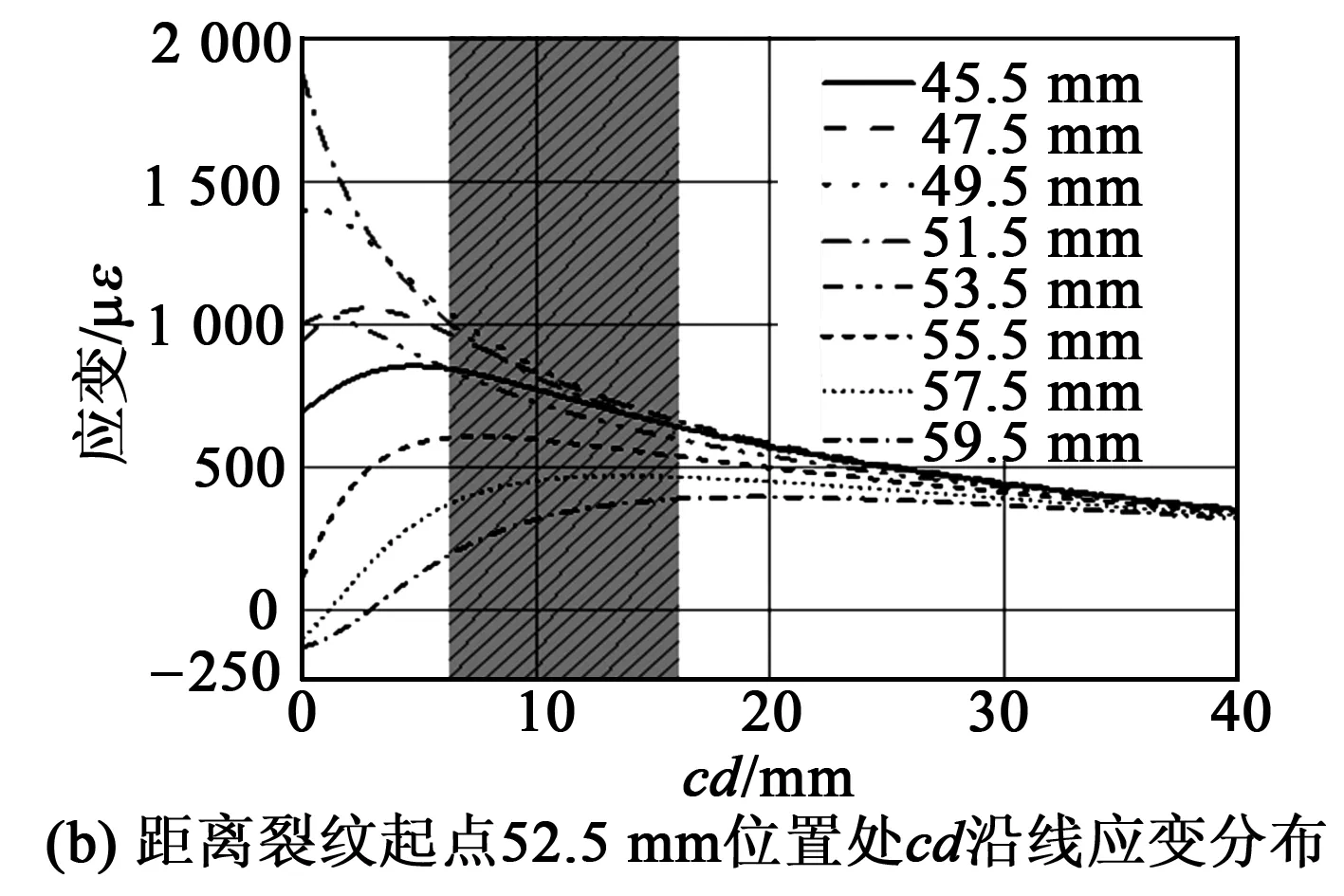
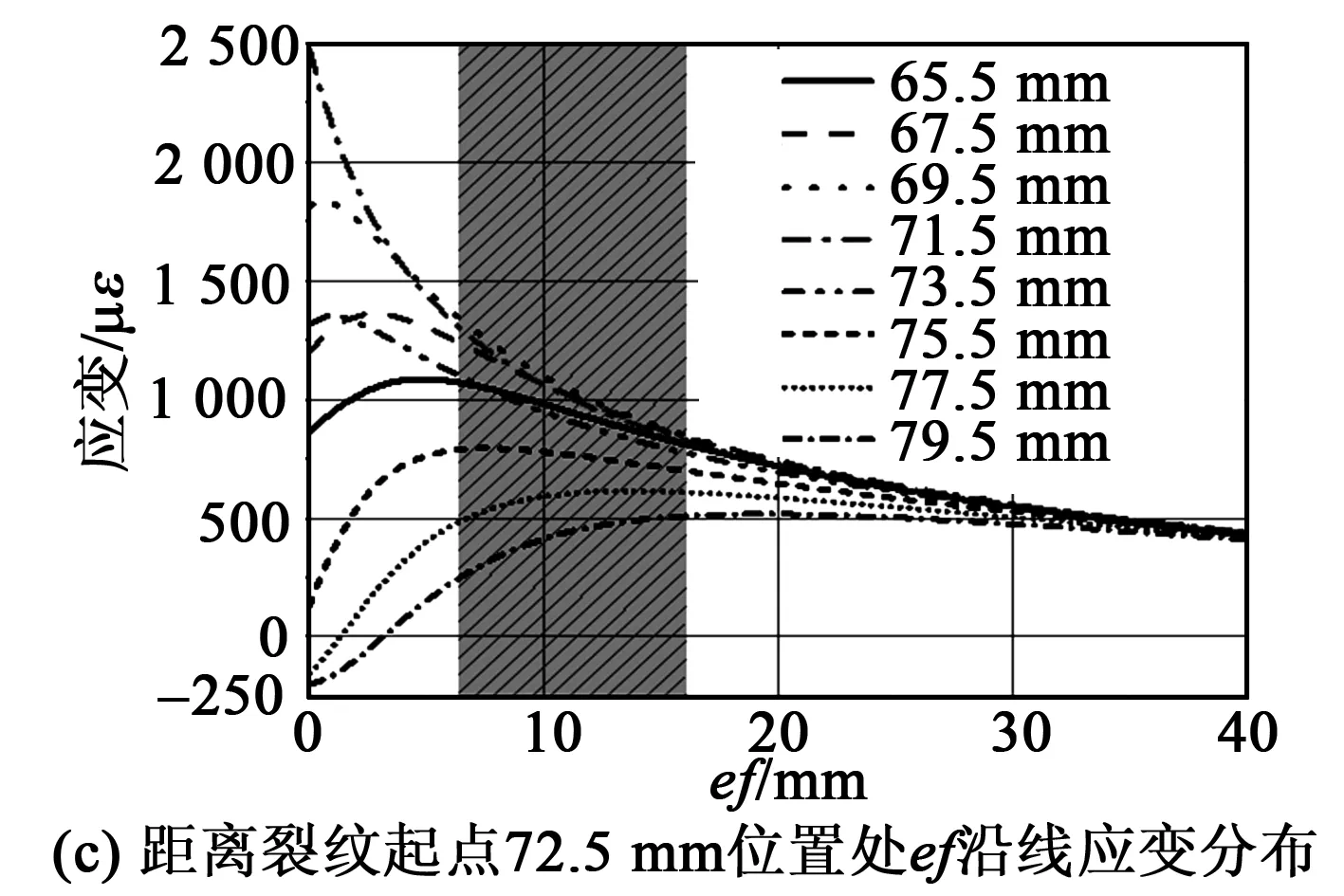
圖5 不同裂紋長度下3個計算區域應變分布
圖5(a)為ab沿線在裂紋從25.5 mm擴展至39.5 mm時的應變分布情況。由圖可知,裂紋在從25.5 mm擴展至31.5 mm過程中,ab沿線應變峰值逐漸增大,應變峰值點隨裂紋擴展往a方向移動。而當裂紋從31.5 mm擴展至39.5 mm過程中,應變峰值逐漸減小,應變峰值隨裂紋擴展向b方向移動。此外,在靠近裂紋擴展路徑a點附近應變梯度大,沿a至b方向的應變變化趨于平緩。
圖5(b)為cd沿線在裂紋從45.5 mm擴展至59.5 mm時的應變分布情況。由圖可知,裂紋在從45.5 mm擴展至51.5 mm過程中,cd沿線的應變峰值逐漸增大,應變峰值往c點方向移動。而在裂紋長度從51.5mm擴展至59.5 mm過程,應變峰值逐漸減小,應變峰值隨裂紋擴展向d點方向移動。在靠近裂紋擴展路徑c點附近應變梯度大,沿c至d方向的應變變化趨于平緩。
圖5(c)為ef沿線在裂紋從65.5 mm擴展至79.5 mm時的應變分布情況。由圖可知,在裂紋從65.5 mm擴展至71.5 mm過程中,ef沿線應變峰值逐漸增大,應變峰值向e點方向移動。在裂紋長度從71.5 mm擴展至79.5 mm過程中,應變峰值逐漸減小,應變峰值隨裂紋擴展向f方向移動。在靠近裂紋擴展路徑e點附近應變梯度大,沿e至f方向的應變幅值趨于平緩。
根據數值仿真結果,為及時獲取裂紋擴展引起的局部應變變化信息,FBG傳感器應盡量粘貼在應變梯度較大區域即靠近裂紋擴展路徑的位置。圖5中陰影部分的沿線位置為FBG傳感器粘貼位置。
3 試驗系統
試驗系統主要由FBG傳感器、MOI光纖光柵解調儀、MTS疲勞試驗機、計算機及鋁合金單邊缺口試驗件構成,如圖6所示。試驗最大疲勞載荷為25 kN,應力比R=0.1,加載頻率為10 Hz。

圖6 疲勞裂紋擴展光纖光柵監測試驗系統
根據有限元分析結果,沿裂紋擴展方向分別將FBG1、FBG2和FBG3依次布置在距離缺口20 mm、40 mm和60 mm處。FBG傳感器軸向應與載荷加載方向保持平行,設置傳感器與裂紋擴展路徑垂直間距10 mm。
疲勞裂紋擴展過程中,借助DMS電子顯微鏡觀測裂紋,同時用直尺測量裂紋擴展的長度。利用20 kN恒定載荷拉伸試件,獲取特定裂紋長度對應FBG傳感器中心波長。
4 實驗結果與討論
4.1 裂紋擴展過程FBG傳感器中心波長響應特征
不同裂紋擴展過程對應的FBG傳感器ΔλB響應曲線,如圖7所示。
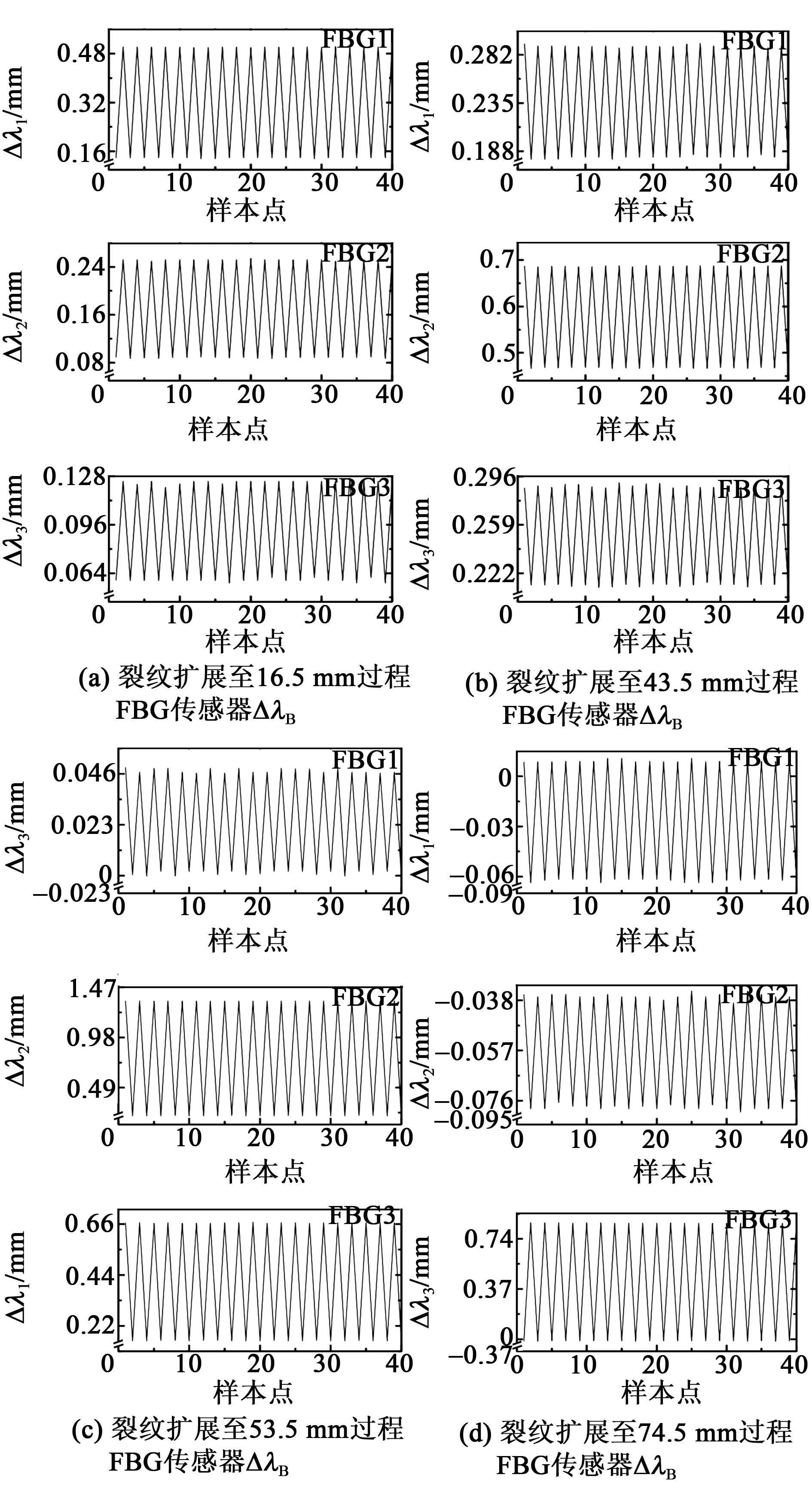
圖7 不同裂紋擴展過程對應的FBG傳感器動態響應曲線
定義裂紋尖端與FBG1、FBG2、FBG3軸向在裂紋擴展路徑上的投影點的間距依次為d1、d2、d3,FBG1、FBG2、FBG3對應中心波長偏移量依次為Δλ1、Δλ2、Δλ3。由圖7可知,FBG傳感器中心波長偏移量呈現與循環載荷同頻的正弦波形式。
對于圖7(a),裂紋擴展至FBG1前,d1
對于圖7(c),裂紋擴展在FBG2和FBG3之間且靠近FBG2的區域,d2
4.2 不同裂紋長度對應的FBG中心波長響應特征
當裂紋依次擴展至15.0 mm、19.5 mm、27.5 mm、34.5 mm,39.5 mm、47.5 mm、53.5 mm、57.5 mm、65.5 mm、74.5 mm時,分別記錄3個不同位置的FBG傳感器中心波長偏移量,得到3個FBG中心波長偏移量與不同裂紋長度之間關系曲線,如圖8所示。

圖8 不同裂紋長度對應的FBG傳感器中心波長偏移量
由圖8可知,3個FBG傳感器中心波長偏移量均隨著裂紋擴展先增大后減小,且在FBG粘貼位置附近中心波長偏移量出現峰值。此響應特征為利用FBG中心波長偏移量,實現疲勞裂紋監測與擴展預測提供了依據。
4.3 裂紋擴展位置預測模型
根據前述可知,FBG中心波長偏移量與裂紋長度有關,可利用不同位置粘貼的FBG傳感器監測鋁合金板疲勞裂紋擴展趨勢。
借助多項式或指數函數擬合,得到裂紋擴展長度與FBG中心波長偏移量間擬合曲線關系模型,定義裂紋長度為x,FBG1、FBG2和FBG3中心波長偏移量分別為Δλ1、Δλ2和Δλ3,則兩者關系表達式為
Δλ1=0.567exp(-((x-22.91)/8.574)2)+
0.562exp(-((x-32.72)/9.831)2)-
0.019
(3)
Δλ2=0.617exp(-((x-49.03)/10.56)2)+
0.625exp(-((x-38.63)/16.24)2)-
0.055
(4)
Δλ3=0.898 45-0.168 78x+0.011 24x2-
3.335 48×10-4x3+4.536 23×10-6x4-
1.908 91×10-8x5-4.519 41×10-11x6
(5)
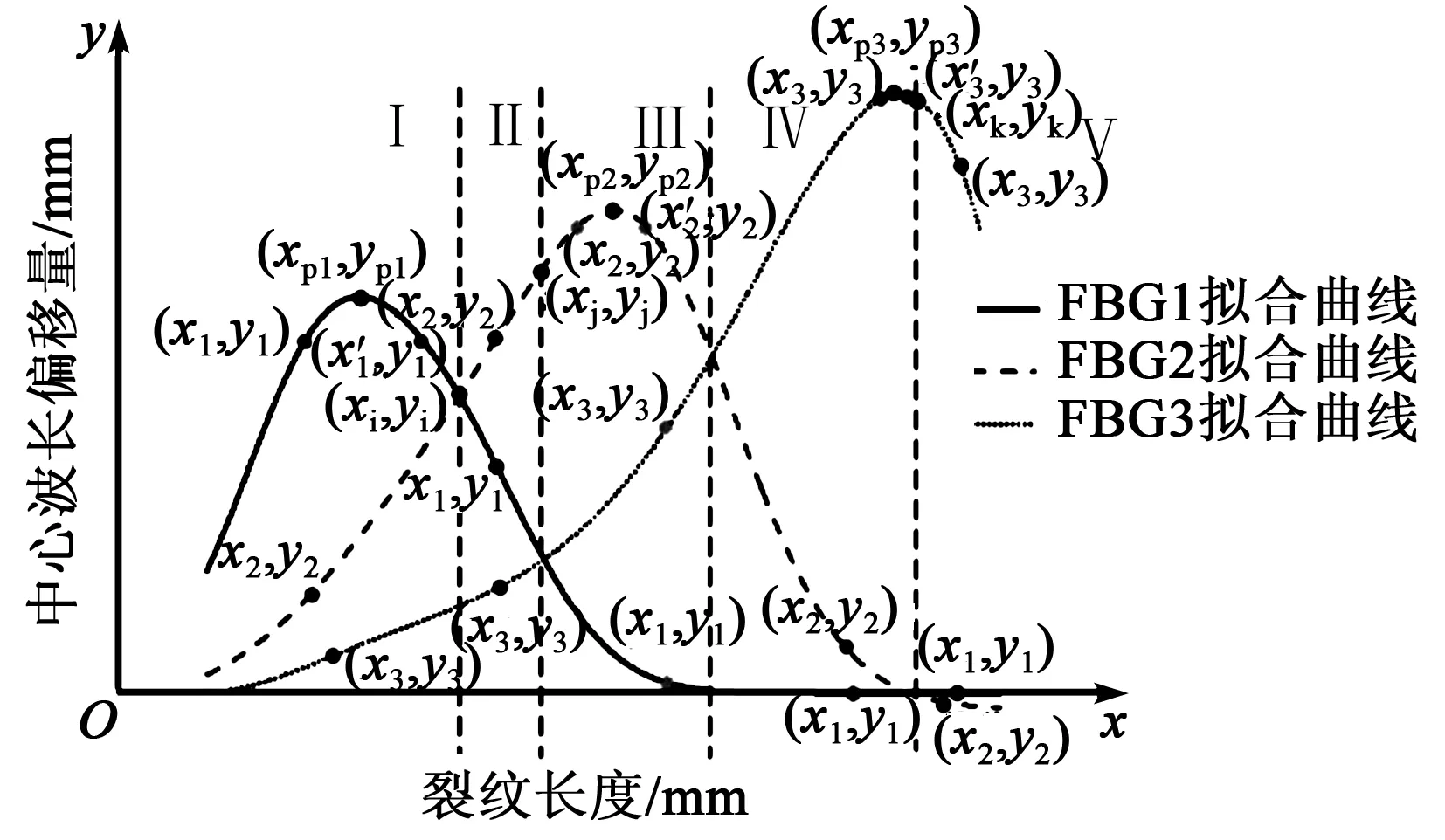
4.3.1 裂紋所在區域定位
對裂紋擴展區域進行劃分,如圖9所示。沿x增大方向,依次將FBG1與FBG2擬合曲線的交點記為(xa,ya),FBG1與FBG3擬合曲線的交點記為(xb,yb),FBG2與FBG3擬合曲線的交點記為(xc,yc),FBG2與FBG1擬合曲線的交點記為(xd,yd),則區域劃分原則為:
1)x≤xa的區域,記為區域I。
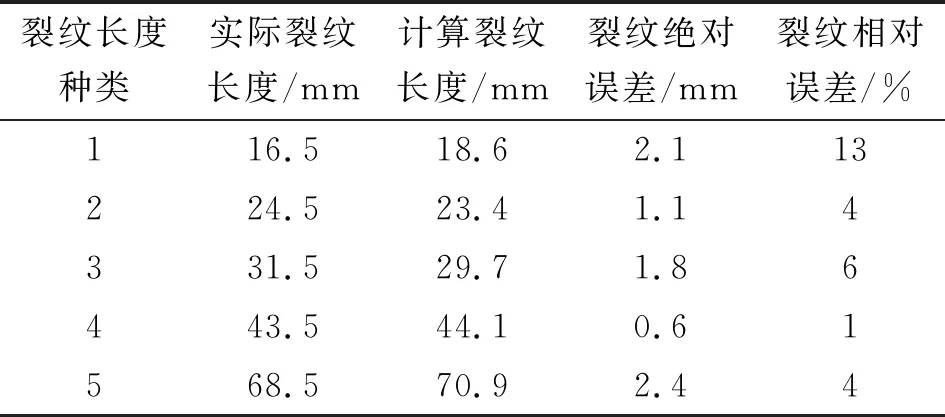
2)xa 3)xb≤x≤xc的區域,記為區域III。 4)xc 5)x≥xd的區域,記為區域V。 圖9 裂紋擴展長度區域劃分 分別計算3個FBG傳感器中心波長偏移量,記為ΔλFBG1, ΔλFBG2, ΔλFBG3,根據3個傳感器中心波長偏移量數值大小關系和擬合函數關系模型,確定裂紋擴展所在區域,具體確定原則為: 1) 若ΔλFBG1>ΔλFBG2>ΔλFBG3,則裂紋擴展在區域I。 2) 若ΔλFBG2>ΔλFBG1>ΔλFBG3,則裂紋擴展在區域II。 3) 若ΔλFBG2>ΔλFBG3>ΔλFBG1,則裂紋擴展在區域III。 4) 若ΔλFBG3>ΔλFBG2>ΔλFBG1,則裂紋擴展在區域IV。 5) 若ΔλFBG3>ΔλFBG1>ΔλFBG2,則裂紋擴展在區域V。 4.3.2 裂紋長度辨識 設ΔλFBG1=y1, ΔλFBG1=y2,ΔλFBG3=y3,FBG1、FBG2和FBG3擬合曲線上其對應的坐標點分別為(x1,y1)、(x2,y2)和(x3,y3),與之具有相同y值的坐標分別為(x′1,y1)、(x′2,y2)和(x′3,y3),如圖10所示。 圖10 裂紋擴展長度辨識 4.3.2.1 步驟一 1) 當裂紋擴展至區域I,FBG1擬合曲線存在非單調區間,FBG1、FBG2曲線在I、II區域的分界線交點記為(xi,yi),FBG1曲線的峰值坐標記為(xp1,yp1); 若y1 若yi≤y1 a.若x2、x3≤xp1,則將x1、x2、x3作為初步預測裂紋長度值。 b.若x2、x3>xp1,則將x′1、x2、x3作為初步預測裂紋長度值。 c.若x2≤xp1≤x3,則將min(|x2-x1|,|x3-x′1|)的x1或x′1與x2、x3作為初步預測裂紋長度值。 d.若x3≤xp1≤x2,則將min(|x3-x1|,|x2-x′1|)的x1或x′1與x2、x3作為初步預測裂紋長度值。 e.若y1=yp1,則將xp1、x2、x3作為初步預測裂紋長度值。 2) 當裂紋擴展至區域II,則直接將x1、x2、x3作為初步預測裂紋長度值; 3) 當預測裂紋擴展至區域III,與區域I求解方法類似,將FBG2曲線峰值坐標記為(xp2,yp2),FBG1、FBG3擬合曲線在II、III區域分界線交點橫坐標記為xj,再將xj代入FBG2曲線,計算得到相應坐標點為(xj,yj)。 若y2 若yj≤y2 a.若x1、x3≤xp2,則將x1、x2、x3作為初步預測裂紋長度值。 b.若x1、x3>xp2,則將x1、x′2、x3作為初步預測裂紋長度值。 c.若x1≤xp2≤x3,則將min(|x2-x1|,|x3-x′2|)的x2或x′2與x1、x3作為初步預測裂紋長度值。 d.若x3≤xp2≤x1,則將min(|x3-x2|,|x1-x′2|)的x2或x′2與x1、x3作為初步預測裂紋長度值。 e.若y2=yp2,則將x1、xp2、x3作為初步預測裂紋長度值。 4) 當裂紋擴展至區域IV,與區域III求解方法類似,將FBG3曲線峰值坐標記為(xp3,yp3),FBG1、FBG2擬合曲線在IV、V區域分界線交點橫坐標記為xk,再將xk代入FBG3曲線,計算得到相應坐標點為(xk,yk)。 若y3 若yk≤y3 a.若x1、x2≤xp3,則將x1、x2、x3作為初步預測裂紋長度值。 b.若x1、x2>xp3,則將x1、x2、x′3作為初步預測裂紋長度值。 c.若x1≤xp3≤x2,則將min(|x3-x1|,|x2x′3|)的x3或x′3與x1、x2作為初步預測裂紋長度值。 d.若x2≤xp3≤x1,則將min(|x3-x2|,|x1-x′3|)的x3或x′3與x1、x2作為初步預測裂紋長度值。 e.若y3=yp3,則將x1、x2、xp3作為初步預測裂紋長度值。 5) 當裂紋擴展在區域V,直接將x1、x2、x3作為初步預測裂紋長度值。 4.3.2.2 步驟二 將各FBG傳感器對未知長度裂紋的響應中心波長偏移量絕對值占比作為權值,即 (6) (7) (8) 將步驟一中由FBG1、FBG2和FBG3擬合曲線所計算的初步預測裂紋長度值分別記為xFBG1、xFBG2和xFBG3,對3個初步預測裂紋長度值進行加權,可確定出未知裂紋最終預測長度為 (9) 試驗中以實際裂紋長度16.5 mm、24.5 mm、31.5 mm、43.5 mm、68.5mm進行預測效果驗證,如表1所示。由表1可以看出,裂紋擴展長度的預測絕對誤差最大為2.4 mm,最小為0.6 mm,平均誤差為1.6 mm。 表1 裂紋擴展長度預測結果 本文針對鋁合金單邊缺口試件結構,提出一種基于分布式光纖光柵傳感器的鋁合金結構疲勞裂紋擴展監測方法。 1) 借助有限元法獲取鋁合金單邊缺口試件在疲勞載荷作用下裂紋擴展的應變場分布規律,確定了FBG優化布局位置。 2) 采用疲勞試驗方法,得到FBG傳感器中心波長偏移量與疲勞裂紋擴展之間關系,分別提出了裂紋區域定位與擴展長度預測方法。 3) 預測結果表明,裂紋擴展長度的預測絕對誤差最大為2.4 mm,最小為0.6 mm,平均誤差為1.6 mm。該預測方法快速簡便,能有效辨識疲勞裂紋擴展位置。 4) 研究成果能為及時準確監測航空航天器金屬結構疲勞裂紋演化趨勢,實現結構剩余壽命評估提供技術支撐。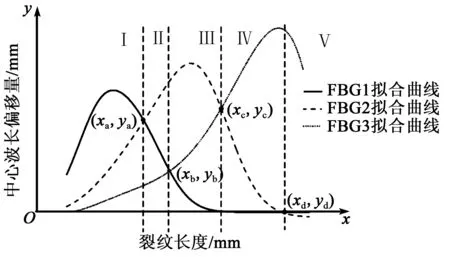
4.4 裂紋長度預測結果
5 結論

