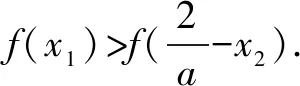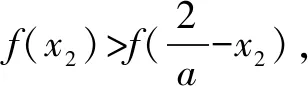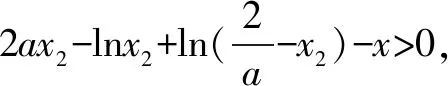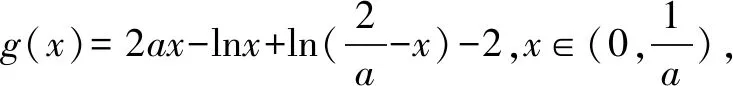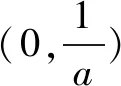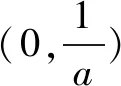與函數零點有關的證明問題解決之我見
徐敏亞
(江蘇省梅村高級中學 214112)
2018年9月10號,全國教育大會在北京召開.這次大會主要研究培養什么人,怎樣培養人,為誰培養人這一根本問題,而高中數學核心素養的頒布指明了在數學學科方面通過高中教育我們培養的學生具有什么樣的核心素養以及怎樣培養數學素養這兩個問題,它是全國教育大會精神在數學學科方面的具體體現.高中數學核心素養包括:數學抽象,邏輯推理,數學建模,直觀想象,數學運算和數學分析這六個方面,其中數學抽象放在了第一位,可見其重要性.數學抽象是指舍去事物的一切物理屬性,得到數學研究對象的思維過程,它貫穿于高中教育階段數學教育的全過程,甚至可以延續到大學、研究生階段的數學教育,而教會學生掌握并使用這個核心素養去解決問題正是培養什么人的關鍵.
眾所周知,與函數零點有關的證明問題在近幾年的高考和各種模考中作為熱點以壓軸題的形式給出,很多學生對待此類問題往往是束手無策,而且此類問題變化多樣,有些題型是不含參數的,但更多的題型又是含有參數的.此類問題處理的手段有很多,方法也有很多,但其實最常見的處理方法就兩種,下面我們通過兩個例題一一來探索.
一、消去參數,構造新函數,利用新函數的單調性解決問題

設x1,x2是函數y=f(x)的兩個零點,且x1 證明∵x1,x2是y=f(x)的兩個零點, 要證x1x2-x2 ∵x1 ∴g(t)在t∈(1,+∞)上單調遞增. ∴g(t)>g(1)=ln1+1-1=0, 又設h(t)=lnt-t+1(t>1)即證h(t)<0. ∴h(t)在t∈(1,+∞)上單調遞減. ∴h(t) 即lnt-t+1<0,得證. 綜上:x1x2-x2 招式分析函數零點的證明問題其實就是導數的應用問題,呈現的形式往往非常簡潔,涉及函數的雙零點和一個參數,是一個多元的數學問題,我們面對這類問題很自然地就會想方設法消去參數,從而使得多元問題變為雙元問題.不管待證的是兩個變量的不等式還是導函數值的不等式,解決的策略都是把雙變量的問題轉化為一元變量的問題求解,而途徑就是通過換元構造一個新的一元函數,利用新函數的單調性解決問題. 例2設函數f(x)=ax-lnx-1(a>0). 證明∵f(x)=ax-lnx-1, ∵a>0,x>0, 又∵f(x1)=f(x2)=0,且x1>x2, 又f(x1)=f(x2), 招式分析此類問題也稱之為極值點的偏移問題,由于思 路固定,所以通常情況下求導比較復雜,計算時需細心.解決口訣:極值偏離“對稱軸”,構造函數覓行蹤;四個步驟環相扣,兩次單調隨其后. 總之,在高考創新試題層出不窮的大環境下,學生首先要掌握基本的知識方法和解題策略,就是我們一直強調的通性通法,對新題、難題的突破,就是需要在掌握好雙基的前提下用數學能力提煉抽象出問題的本質,淡化特殊技巧,重視通性通法,去模式化的解題策略,以不變應萬變,培養學生分析問題、解決問題的能力.只有學生學會自我分析,用數學抽象的核心素養把問題轉化為熟悉的問題,從而用熟知的知識方法去解決未知的創新試題,這樣才能真正培養學生的能力,才是數學核心素養在高中數學教育的真正體現.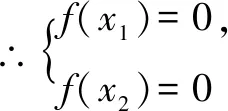

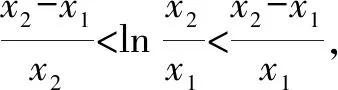

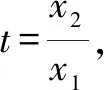




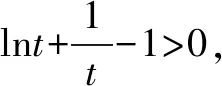

二、保留參數,構造新函數,利用原函數和新函數的兩次單調性解決問題