錯位相減法的拓展及應用
黃冬明
(安徽省合肥市巢湖市第四中學 238000)
一、錯位相減法的背景
在高中數學“等比數列前n項和”一節中,給出了等比數列{an}的前n項和Sn的推導方法:
Sn=a1+a2+…+an-1+an即
Sn=a1+a1q+a1q2+…+a1qn-2+a1qn-1①,
等號兩邊同時乘以公比q得
qSn=a1q+a1q2+…+a1qn-2+a1qn-1+a1qn②.
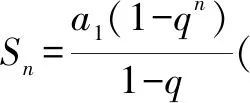
這類前n項和的計算首先在等式的兩邊同時乘以公比q,然后將新得到的等式和原等式相減,這種方法叫做錯位相減法.
二、什么樣的求和可以運用“錯位相減法”
對于數列形如cn=an·bn,且{an},{bn}分別是等差數列和等比數列的求和問題就可以運用錯位相減法.其一般形式的概括如下:
Sn=a1b1+a2b2+a3b3+…+an-1bn-1+anbn,
即Sn=a1b1+a2b1q+a3b1q2+…+an-1b1qn-2+anb1qn-1①,
①×q得
qSn=a1b1q+a2b1q2+a3b1q3+…+an-1b1qn-1+anb1qn②.
①- ②得
(1-q)Sn=a1b1+d(b1q+b1q2+…+b1qn-2+b1qn-1)-anb1qn.
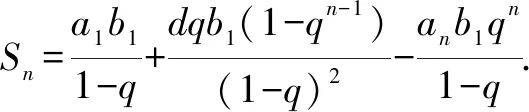
三、錯位相減法的運用
例1若數列cn=n·2n,求數列{cn}的前n項和Sn的表達式.
分析數列cn=n·2n可以看成是一個等差數列an=n和一個等比數列bn=2n的乘積,故可以用錯位相減法來計算.
解Sn=1×2+2×22+3×23+…+(n-1)·2n-1+n·2n①,
2Sn=1×22+2×23+3×24+…+(n-1)·2n+n·2n+1②.
①- ②,得
-Sn=1×2+22+23+…+2n-n·2n+1,
所以Sn=(n-1)·2n+1+2.
錯位相減法計算出錯主要有如下幾個方面:學生不知道何時使用錯位相減法,兩式相減時容易漏項或者符號出錯,最后結果化簡時學生信心不足.筆者在課下反思如何減少錯誤,能否用新方法代替錯位相減法.
四、錯位相減法的拓展及應用——裂項法
我們仍然以cn=n·2n為例,我們將{cn}的表達式進行變形如下n·2n=(an+b)·2n-[a(n+1)+b]·2n+1=2n·(-an-2a-b),則a=-1,b=2.
因此n·2n=(-n+2)·2n-[-(n+1)+2]·2n+1,則
Sn=(-1+2)×2-(-2+2)×22+(-2+2)×22-(-3+2)×23+…+(-n+2)·2n-[-(n+1)+2]·2n+1.
仔細觀察這個式子,這個式子從第二項開始,前一項和后一項互為相反數,則Sn=1×2-[-(n+1)+2]·2n+1=(n-1)·2n+1+2.
這個計算方法將數列cn=n·2n變成兩個數列的差的形式,且求和時運用到類似裂項求和的思路.前面的變形計算比錯位相減復雜一些,但求和過程很簡單.
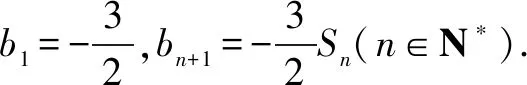
(1)求數列{an}和{bn}的通項公式:
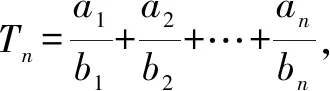

(2)方法一:(錯位相減法)
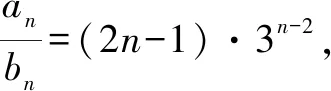
故3Tn=-2+3×31+5×32+7×33+…+(2n-3)×3n-2+(2n-1)×3n-1②.
方法二:(裂項法)
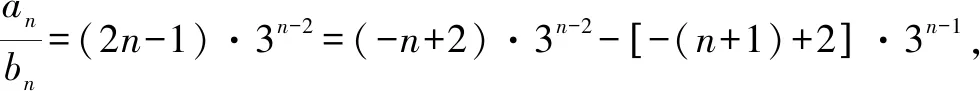
如果學生能夠掌握此法的本質,那對數列求和真能起到質的飛躍,真正做到化“腐朽”為“神奇”. 但筆者認為,對大多數學生來講只要認清數列本身的特點,選擇適合的方法即可.

