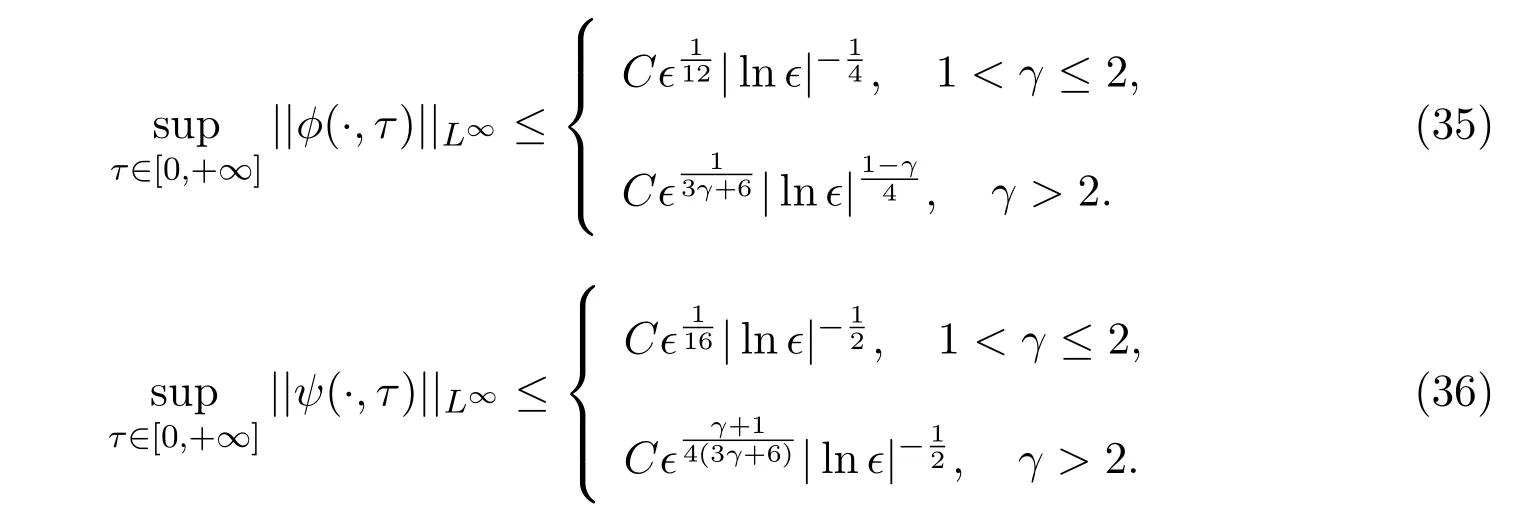一維可壓縮等熵Navier-Stokes方程稀疏波在流近似下的零耗散極限
王金妮,劉進靜
(西北大學數學學院,陜西 西安 710127)
1 引言
眾所周知,一維可壓縮等熵Euler方程組為:
其中ρ(x,t)≥0,u(x,t)分別表示流體的密度和速度,表示壓力,γ>1為絕熱指數.當賦予方程組(1)如下的初值:

其中 (ρ±,u±)均是常數,則 Riemann問題 (1)-問題 (2)的解包含激波、稀疏波和真空[1-2],在這兩種非線性波中,僅稀疏波能夠與真空連接.
本文考慮當Euler方程組(1)稀疏波解的一端與真空連接時,如下一維可壓縮等熵Navier-Stokes方程組的零耗散極限:

其中?>0為常黏性系數.
隨著黏性的消失,黏性流的解強收斂到對應無黏流的解,這類問題即為零耗散極限問題,它是可壓縮黏性流體中一類十分重要且具有開放性的問題.當無黏流不包含奇性時,可由經典標量方法得到零耗散極限,而當無黏流包含奇性如激波和真空時,零耗散極限問題富有挑戰性.對于可壓縮等熵Navier-Stokes方程組,文獻[3]首先考慮了包含初始層且Euler方程組的解是單個激波的情形,證明了隨著黏性的消失,方程的解趨于黏性激波,基于上述結果,文獻[4]證明了在沒有初始層的情況下,當Euler方程組包含稀疏波解且不包含真空時,可壓縮等熵Navier-Stokes方程組稀疏波解的零耗散極限,且得到一致收斂率.若Euler方程組(1)的初值只在無窮遠處無真空,文獻[5]利用補償緊致性的方法得到了方程組(3)的黏性消失極限.關于兩個激波復合的情形可以參考文獻[6-7].對于非等熵Navier-Stokes方程組的零耗散極限也有了豐富的研究成果[8-13],特別地,文獻[10]考慮了可壓熱傳導Navier-Stokes方程組激波解的零耗散極限問題;文獻[13]對于稀疏波與接觸間斷波疊加的情形進行了研究.此外,對于如下黏性雙曲守恒律也已經有了一些有意義的成果:

文獻[14]利用匹配漸近展開方法研究了激波的黏性消失極限,后來此結果被文獻[15]推廣到包含初始層的情形.文獻[16]在BV空間中研究了解的黏性消失極限問題,隨后,文獻[17-18]對這一結果進行了改進和推廣.
近年來,文獻[19]研究了當Euler方程組(1)的解為2-稀疏波+真空時,Navier-Stokes方程組(3)的零耗散極限,并對方程組(1)賦予Riemann初值:

且得到連接真空狀態 (0,u1)到 (ρ+,u+)的 2-稀疏波 (ρr2,mr2=ρr2ur2):

其中mr2表示動量,分別表示方程組(1)的特征值和2-Riemann不變量.然后 Huang等人對與真空連接的2-稀疏波 (ρr2,mr2)進行截斷處理,并且構造了 Navier-Stokes方程組 (3)的一列解,當黏性?→0時此列解收斂于與真空連接的2-稀疏波(ρr2,mr2),并得到一致收斂率估計.另外,關于黏性依賴于密度的Navier-Stokes方程解的零耗散極限也已經有許多學者研究,具體可參見文獻[20-21].
事實上,探究當稀疏波與真空連接時Navier-Stokes方程組(3)的解的零耗散極限關鍵之一在于如何控制稀疏波中由真空引起的退化,本文將利用流近似方法[22-23]控制退化.從物理學的觀點來看,流體是分子結構不抵抗外部剪切力的物質,即使是最小的力也會引起流體粒子的變形;從數學上講,很小的力可以看作是力學上的流擾動,進而發現合理的擾動可以用來控制流體的某些動力學行為,因此,流近似可以用來控制真空附近的退化.
首先,本文對Euler方程組(1)進行流擾動,即得到擾動Euler方程組:

其中密度ρ≥2ν,ν>0為依賴于黏性?的參數.本文將選取ν=?a|ln?|,其中a由下文(15)式給出.當ν→0時,上述方程組形式上變為Euler方程組(1).事實上,方程組(6)是嚴格雙曲型的,它有兩個互異的特征值:


即這兩個特征場都是真正非線性的.此外,i-Riemann不變量定義為
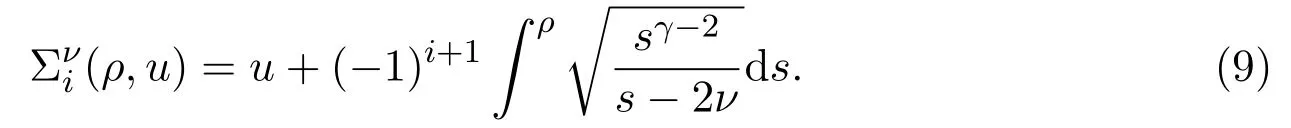
解 Riemann問題 (6),問題 (2),可以得到兩類基本波解,即激波 (S1,S2)和稀疏波 (R1,R2),(更多相關細節參見文獻 [22]).因此能夠得到 5種結構的解 (見圖 1),特別地,當 (u+,ρ+)∈V(u?,ρ?)時,Riemann解包含 2個稀疏波和 1個常密度狀態 (ρ=2ν).通過對比發現,Riemann問題 (1),問題 (2)的解包含真空狀態,而Riemann問題(6),問題(2)的解已不包含真空狀態.換言之,已經控制了稀疏波中真空引起的退化.

圖1 方程組(6)Riemann解的結構
本文僅考慮2-稀疏波.如果給方程組(6)賦予Riemann初值:

即左狀態為常密度,那么連接 (2ν,u?)到 (ρ+,u+)的 2-稀疏波解

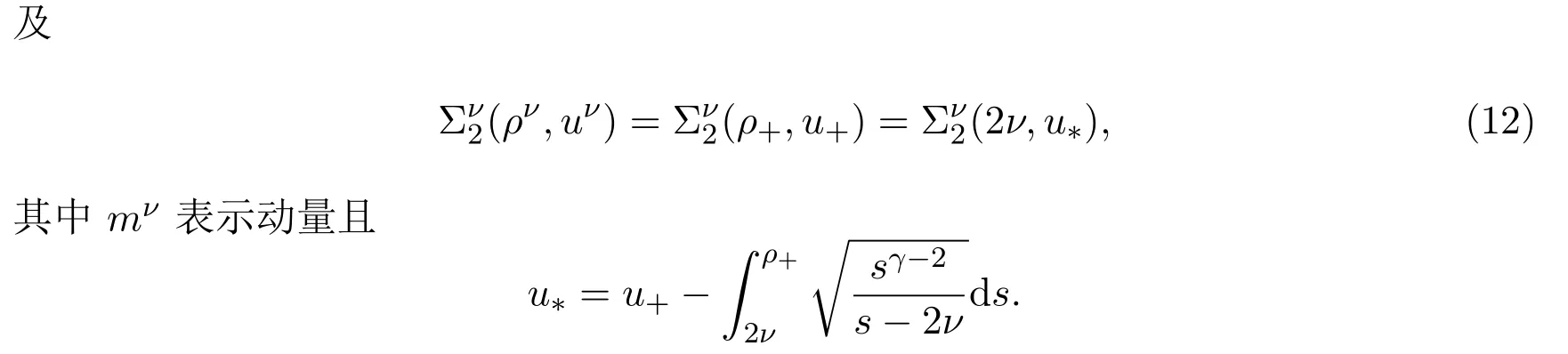
由顯示解公式可知當ν→0時,2-稀疏波 (ρν,mν)收斂于由 (4)式和 (5)式定義的 (ρr2,mr2).因此有下面的引理:
引理 1.1存在一個常數ν0∈(0,1),使得對ν∈(0,ν0],t>0有:

然后,本文利用 Burgers方程對2-稀疏波 (ρν,mν)進行光滑逼近,構造其近似稀疏波.
下面敘述本文的主要結論:
定理 1.1設由(4)式和(5)式定義的是Euler方程組(1)的一端與真空連接的2-稀疏波解,且給方程組(3)賦予初值(27),則存在適當小的正常數?0>0,對任意的?∈(0,?0),可以構造方程組(3)的一列光滑全局解滿足:

且當?→0時,(ρ?,m?)(x,t)逐點收斂到 (ρr2,mr2)(x,t)(除點 (0,0)外).
進一步,對于任意給定的常數h>0,存在一常數Ch>0(不依賴于?),成立:

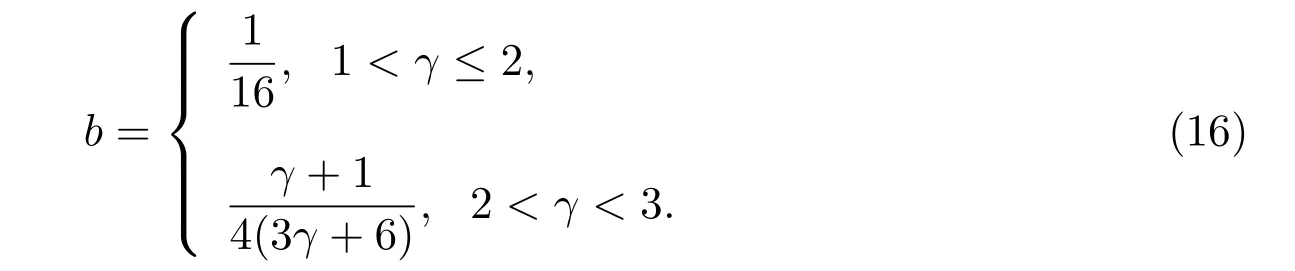
注1.1(i)本文介紹了另一種方法,即運用流近似方法研究一維可壓縮等熵Navier-Stokes方程組的零耗散極限.通過以上的分析,可以發現定理1.1中關于?的收斂率與文獻[19]中得到的收斂率不同.
(ii)L2(R)表示定義在R上的平方可積實值函數空間,且范數記為||·||:=||·||L2.
(iii)Hk(R)表示常用的 Sobolev空間,且范數記為||·||k,特別地,||·||0=||·||.
近年來,鋰離子電池的應用已經逐漸擴展到汽車、家電、電動自行車、儲能等領域。2014年,中國鋰離子電池產量達52.87億只,占全球總產量比重達到71.2%, 2018年預計全國鋰電池產量達到121億只,增速22.86%。國內鋰離子電池產業進入快速成長階段,成為全球主要的鋰離子電池生產國和消費國。
(iv)C表示不依賴于?和時間t的正常數.
本文剩余內容結構安排如下:第二部分利用無黏 Burgers方程對 2-稀疏波 (ρν,mν)進行光滑逼近;第三部分給出定理1.1的證明.
2 近似稀疏波
受到文獻 [4,19,24]中部分思想的啟發,本節將利用 Burgers方程建立關于擾動Euler方程(6)稀疏波解的一些必要估計,特別要構造一個光滑稀疏波,使其能夠很好地逼近 2-稀疏波 (ρν,mν).
考慮無黏Burgers方程的Riemann問題:

當w? 參照文獻[4,19,24],2-稀疏波(ρν,mν)可由下面的Burgers方程進行光滑逼近: 其中δ>0是待定小常數.注意到,方程組(19)存在唯一的光滑全局解 引理2.1的證明參見文獻[4,19],這里不再證明. 本節將證明這篇文章的主要結論.記 Navier-Stokes方程組 (3)的解為 (ρ?,u?),為簡便起見,省去(ρ?,u?)的上標,即用 (ρ,u)表示方程組 (3)的解.賦予方程組 (3)如下的光滑初始值 把(28)式-(29)式代入方程組(3),并結合方程組(26)得到 引理 3.1重構問題(30)-問題(32)存在唯一全局解(?,ψ)∈X(0,τ1),并且存在某個充分小的?0>0,使得當0 其中a由方程組(15)給出,因此 隨后的分析中,作出先驗假設 其中a由方程組 (15)給出,[0,τ1(?)]表示解存在的時間區間且τ1(?)依賴于?.容易發現若??1,則ν≥2?a成立.根據先驗假設(37),得到 其中C1,C2是不依賴于?的正常數. 分析發現一旦得到引理3.1,可立即得到定理1.1.另外,方程(30)-方程(32)解的局部存在定理是標準的,本文不再陳述.[0,∞]上的解可由解的局部存在性和一些先驗估計得到,因此這篇文章的主要任務就是得到如下的先驗估計: 引理 3.2(先驗估計) 設 (?,ψ)∈X(0,τ1(?))是重構問題 (30)-問題 (32)的解,其中τ1(?)表示解存在的最大時間且滿足先驗假設(37),則存在充分小的常數?0>0,使得當0 接下來證明引理3.2,證明主要分三步進行. 證明(I)給方程(31)乘ψ得到 即完成了引理3.2的證明. 據此可以斷言τ1(?)=∞.事實上,如果τ1(?)<∞,則可再次利用解在時間τ=τ1(?) 的局部存在性,找到另一時間τ1(?)<τ2(?) 使得解在 [0,τ2(?)]內滿足 (37)式,這與引理3.2中τ1(?)是最大時間矛盾.因此,當?較小但固定時,可以把局部解延拓至全局解.最后,證明定理1.1. 定理 1.1的證明根據引理1.1,引理2.2,引理3.1及ν=?a|ln?|,δ=?a,則對任意給定的常數h>0,存在不依賴于?的常數Ch>0,使得



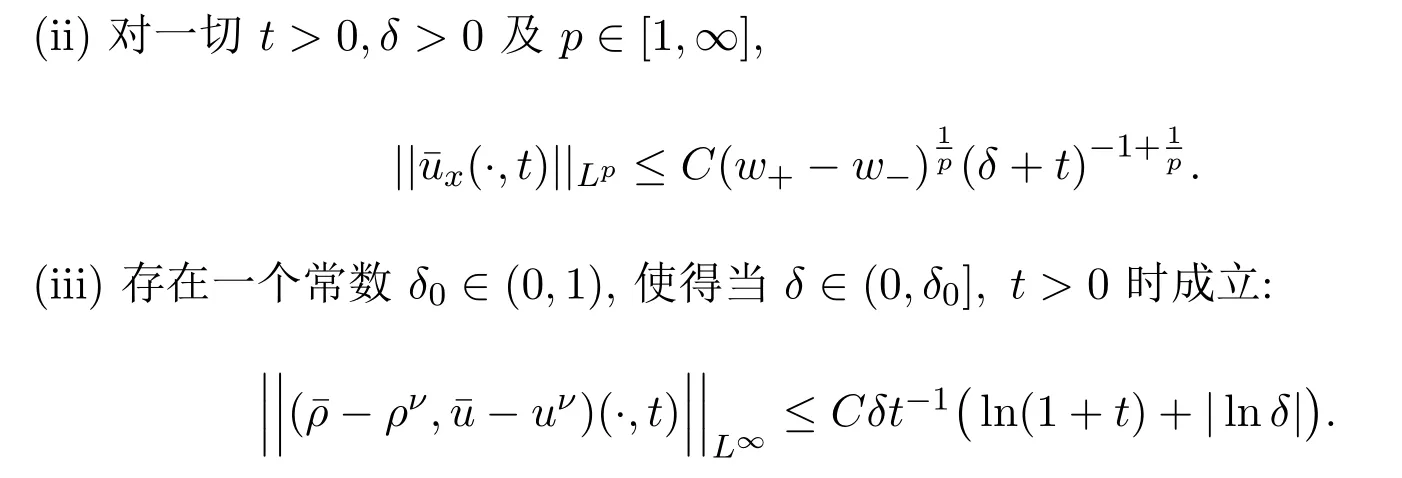
3 定理1.1的證明