不同側風工況下汽車穩定性雙向耦合研究

李舒雅 谷正氣,2 黃泰明 劉 俊 鄭樂典

1.湖南大學汽車車身先進設計制造國家重點實驗室,長沙,4100822.湖南文理學院,常德,415000 3.湖南理工學院機械工程學院,岳陽,414006

0 引言

隨著新能源汽車的快速發展，汽車的輕量化程度不斷提高，氣動阻力不斷減小。然而，當汽車更輕、阻力更小時，其側風穩定性也會更差，進而影響汽車和駕駛員的安全[1]，因此側風穩定性研究十分重要。

由于汽車的運動姿態變化會影響汽車周圍流場的瞬時變化[2-4]，而瞬時變化的流場也會反過來影響汽車的運動姿態[5-6]，因此汽車的運動和流場變化是實時耦合的。目前對汽車在側風作用下的穩定性研究主要采用多自由度汽車動力學模型與空氣動力學模型相耦合的方法[7-9]，以及將風洞試驗結果或流場分析結果單向傳遞給汽車動力學模型進行求解的方法[10-12]。第一種方法對汽車結構進行簡化，不能反映汽車細節結構對汽車穩定性的影響，而第二種方法忽略了汽車在流場中的運動變化對氣動力的影響，因此這兩種方法都不能完全反映汽車在側風下的運動狀態。此外，目前在汽車側風穩定性的評價中，主要采用類似ISO12021中汽車穿過側風區的方式模擬汽車受到的環境側風[7-8]，而汽車在高速路上行駛時，會更多地遇到自然側風的工況。自然側風作用于整個汽車，對汽車的穩定性會產生較大影響。

本文結合兩種方法的優勢，基于能反映汽車實際結構的多體動力學方法(multi body dynamics, MBD)[13-14]和能反映汽車實際瞬態流場特性的大渦模擬(large eddy simulation, LES)方法[7,15]，提出了一種汽車運動與汽車流場實時同步的雙向耦合分析方法。

1 數值計算方法

汽車空氣動力學仿真和汽車多體系統動力學仿真的耦合分析系統見圖1，側風對汽車的影響通過計算流體動力學(computational fluid dynamics, CFD)模型引入，路面和駕駛員對汽車的影響通過MBD模型引入。同時，CFD模型將側風作用下的汽車氣動力通過耦合平臺傳遞給MBD模型進行計算，而MBD模型在氣動力、路面和駕駛員的綜合作用下，將運動反饋給汽車CFD模型，以此實現汽車流場變化和汽車運動變化的實時耦合。

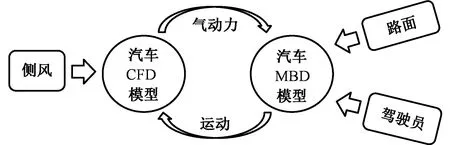
圖1 CFD與MBD雙向耦合分析系統Fig.1 Two-way coupling system of CFD with MBD

本文數值仿真計算采用某汽車1∶1模型(圖2)。車長4.587 m、寬1.799 m、高1.467 m。當車速為100 km/h時，基于車長的雷諾數為8.7×106，因此汽車周圍為高雷諾數湍流流場；同時由于汽車車速低、馬赫數小，因此汽車周圍流場通常被看作不可壓流場。

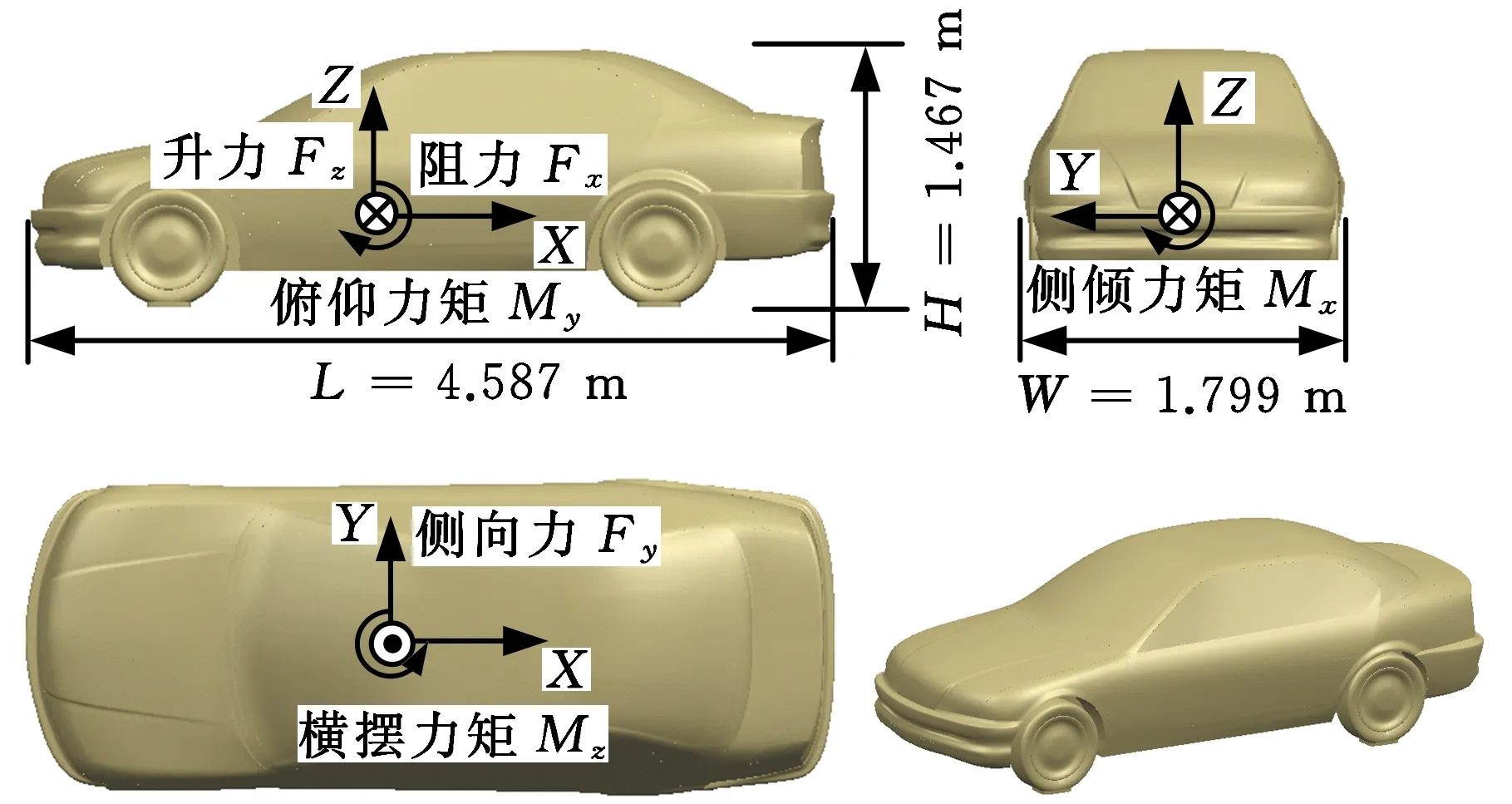
圖2 汽車模型和坐標系Fig.2 Vehicle model and coordinate system

坐標系設置見圖2，坐標原點為該汽車的質心位置，汽車前進方向為X軸負方向，汽車駕駛員右側為Y軸正向。為避免坐標系轉換過程中產生數據誤差，仿真中氣動力的獲取和運動的交換以全局坐標系作為參考。

1.1 數值計算管理方程

1.1.1空氣動力學數值方法

汽車瞬態流場的計算采用LES方法。LES方法中，流場的湍流流動是由不同尺度的渦組成的，其中大型的渦采用直接數值模擬(direct numerical simulation, DNS)方法求解N-S(Navier-Stokes)方程，而對于小型的渦，通過濾波函數過濾之后，利用亞格子模型將小型渦對大渦的影響考慮進去，相較于DNS，LES法既縮短了計算時間，又降低了計算資源要求，同時相較于傳統的湍流模型模型，還提高了計算精度。

經濾波后的基于LES法的非定常不可壓N-S方程可以表示為

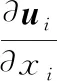
(1)

(2)

(3)

(4)

式中，ui、uj為速度矢量；p為壓力；ρ為空氣密度；ν為空氣的運動黏度；νSGS為亞格子尺度渦黏度；Sij為求解尺度下的應變率張量分量。

本文采用標準Smagorisky模型，式(2)中的亞格子尺度渦黏度νSGS可以描述為

(5)

(6)

式中，cs為Smagorisky模型常數，本文取cs= 0.1[16-17];Δ為網格過濾尺度，可以定義為每個單元體積的立方根；fd為van Direst阻尼方程；y+為距離表面法向的量綱一長度。

1.1.2多體動力學數值計算方程

本文的汽車動力學模型采用多體動力學虛擬樣機模型，采用第一類拉格朗日方程描述各個構件的運動。汽車由若干的構件和約束組成，其中每個構件和約束方程基于全局坐標系可以表示為

(7)

式中，q為廣義坐標變量，由沿三個方向的位置和三個角度組成 ，即qT=(x，y，z，ψ，θ，φ)，其中角度的旋轉采用3-1-3規則；K為該構件的動能；Fq為作用力矩陣；Ck為某個約束副里的第k個約束方程；λk為拉格朗日乘子數組，共有m個作用在該構件上。

將每個構件和運動副的約束方程組合，得到汽車多體系統動力學管理方程：

(8)

式中，Φq為約束方程矩陣。

以上微分-代數方程(differential-algebraic equations, DAE)采用GSTIFF積分器求解[18]，得到各個構件上的運動和作用力。

1.2 空氣動力學計算模型

采用圖3所示的計算域進行空氣動力學計算。其中L為汽車車長，汽車模型距計算域前部入口3倍車長，距尾部出口7倍車長。W為汽車車寬，汽車距左側入口4倍車寬，距右側出口10倍車寬，經計算，計算域的設置滿足阻塞比的要求[19]。計算域前側和左側均為速度入口，縱向速度為100 km/h；后側和右側為壓力出口，大小為大氣壓；汽車車身為無滑移壁面，計算域底部和頂部為滑移壁面。

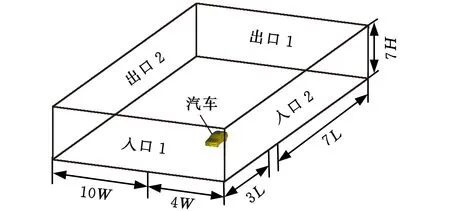
圖3 計算域設定Fig.3 The setup of the fluid domain

汽車在流場中的運動姿態變化由Arbitrary Lagrange-Euler(ALE)動網格方法實現[7]。在本文的CFD仿真中，汽車的運動參數來源于多體動力學模型的計算結果，流場中的汽車得到運動參數后，汽車車身在5個自由度方向產生運動(車身前進方向的自由度用相對風速處理，因此去除了X軸方向的自由度)，汽車周圍的網格在Smoothing和Remesh方法下進行變形和重構。采用商業軟件ICEM CFD在汽車周圍生成四面體非結構網格，為了滿足大渦模擬的壁面網格要求，將車身表面網格拉伸出平行的邊界層棱柱網格[20]，劃分完成網格見圖4。

圖4 計算網格Fig.4 The mesh generation

由于計算網格的數量會影響計算精度，故本文采用幾種不同的網格加密尺寸，在相同的邊界條件下進行仿真計算，并將計算結果與風洞試驗測試結果進行對比，幾種網格驗證方案和結果見表1。由表1可知，風洞試驗氣動阻力系數Cd為0.284，升力系數Cl為-0.047；方案3和方案4網格計算結果相同，與風洞試驗的誤差最小，分別為0.4%和2.1%。考慮到計算時間和計算資源，本文采用網格方案3。

表1 網格驗證結果

根據文獻[21]可知，側風通過入口1和入口2的合成風來模擬，得到的結果與試驗更相符。由于汽車在縱向的自由度由相對速度來考慮，因此，自然側風和ISO12021標準側風在邊界條件上有較大的不同。對于自然側風，其入口1和入口2的合成風邊界條件如圖5所示。自然側風的前部入口和側面入口合成速度相同，其中X方向速度為汽車車速，側向Y的速度為側風風速。Y向速度為時間函數，根據文獻[22]，函數可以寫為

vw(t)=

(9)

式中,vw(t)為隨時間變化的側風速度;vw,max為側風的最大風速，根據ISO12021取20 m/s；ts為余弦段的長度，根據文獻[23]取1.5倍車長對應的時間；td為側風穩定時間，根據文獻[24]，以余弦上升和下降階段的中間位置計算的側風區域長度(ts+td)超過7倍車長時，側風會發展成穩定的湍流，為了研究汽車在瞬態下的穩定性，避免發展成穩定的側向湍流，側風區域取為6倍車長，總側風作用區域為7.5倍車長，滿足ISO12021標準中側風區域寬度不低于20～25 m的要求。

(a)自然側風邊界條件

(b)標準側風邊界條件圖5 側風模擬邊界條件Fig.5 The boundary condition for crosswind simulation

由于汽車在縱向不產生運動，因此環境側風的模擬采用相對運動進行處理[22]，環境側風區域從入口1以車速相對于汽車運動。入口1處合成風速與自然側風一致，入口2處側向風速為時間和空間的函數，可以表示為

F(x,t)=

(10)

式中，v為汽車車速，其余參量的取值與自然側風一致，以便于自然側風與標準側風的對比。

為了使汽車在流場中穩定后開始耦合，側風在耦合開始后0.5 s開始，因此根據上述函數繪制出平移2.5 s的側風風形，如圖6所示。其中圖6a為自然側風，作用于自然側風工況的入口1和入口2；圖6b為標準環境側風，側風沿X軸正向移動，作用于標準側風工況的入口2，標準側風工況的入口1采用與自然側風相同的瞬態側風邊界條件。

(a)自然側風

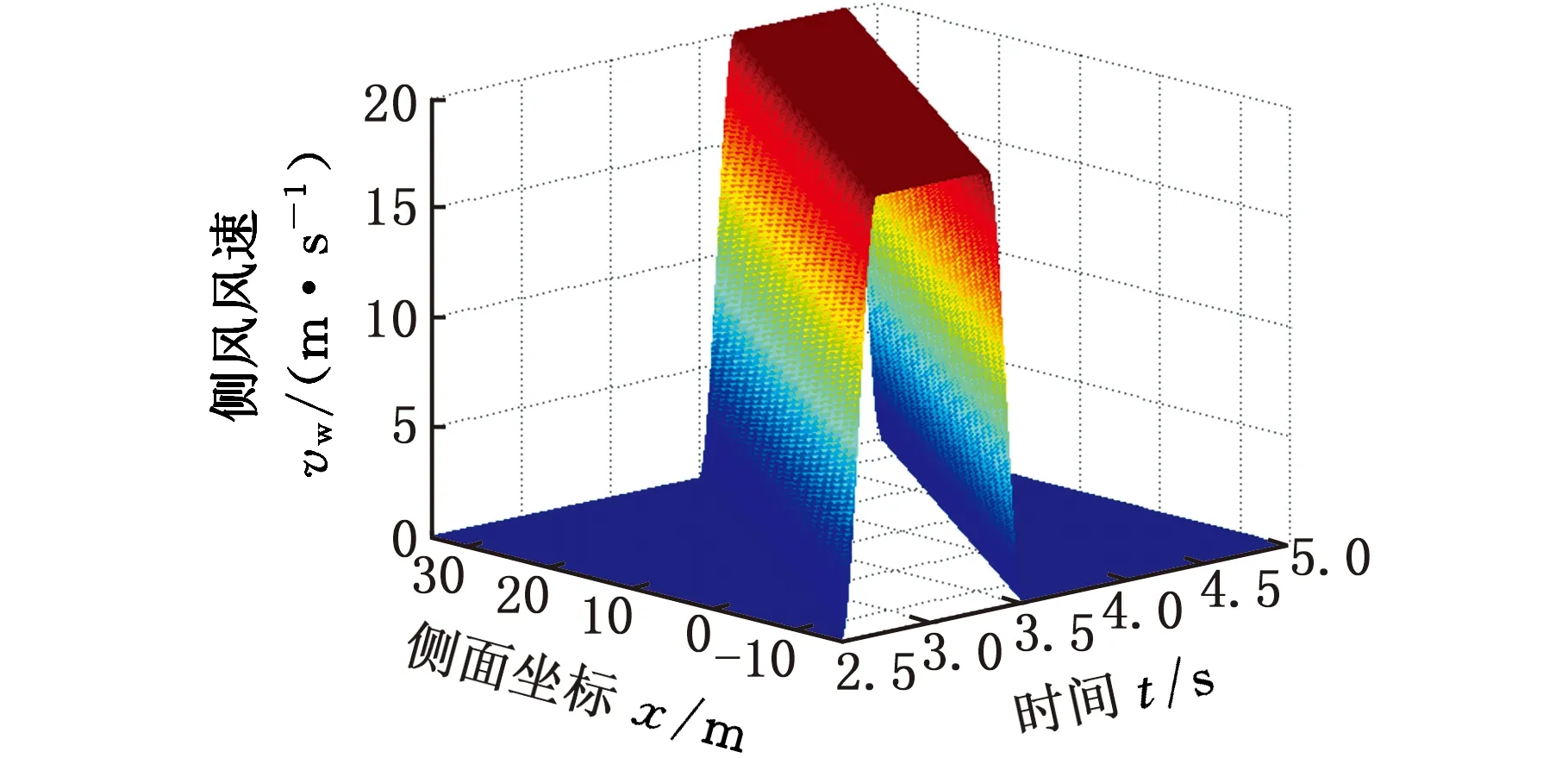
(b)ISO標準側風圖6 自然側風和ISO標準側風模型Fig.6 Natural crosswind and ISO standard crosswind model

1.3 多體系統動力學計算模型

根據如表2所示的汽車整車參數，基于ADAMS/Car建立汽車多體系統動力學模型，包括完整的汽車前后懸架系統、轉向系統、制動系統、車身、輪胎以及路面，如圖7所示。

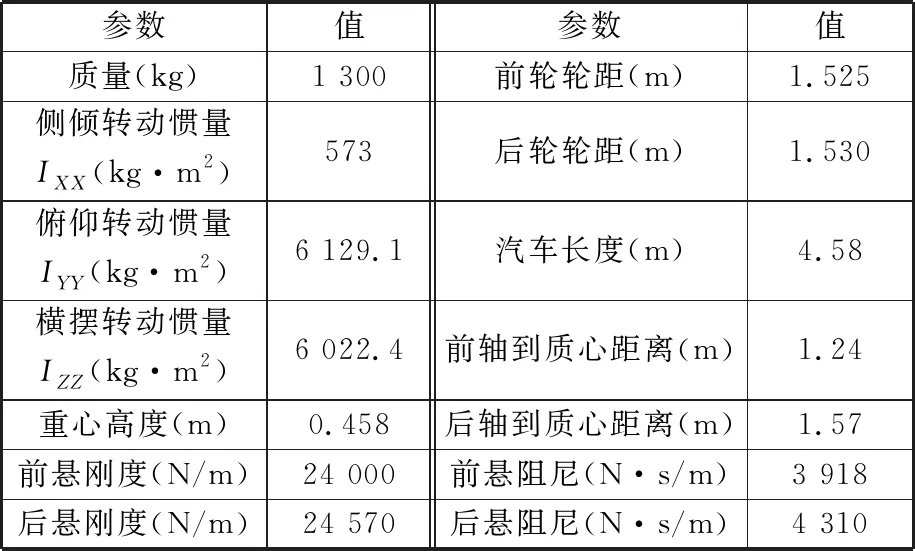
表2 汽車整車參數

根據ISO12021標準，為了減小駕駛員對汽車側風穩定性評價的影響，在本文的側風模擬中，汽車轉向盤始終處于鎖死的狀態，不考慮駕駛員模型的影響。汽車輪胎采用基于魔術公式Pacejka89的185/65R15輪胎，路面采用光滑路面，路面摩擦因數為1.0。氣動六分力作用于汽車剛性車身的質心，并通過運動調試，將汽車的質心高度與CFD模型調整一致。氣動六分力的數值來源于實時的CFD計算，它在每個時間步進行更新，并將質心的運動反饋給CFD模型。

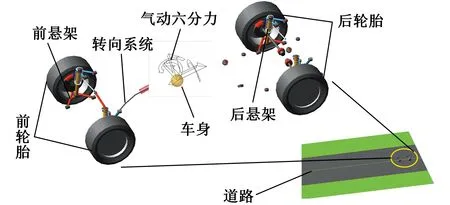
圖7 汽車多體系統動力學模型Fig.7 Vehicle multi body dynamic model

1.4 空氣動力學與多體動力學雙向耦合

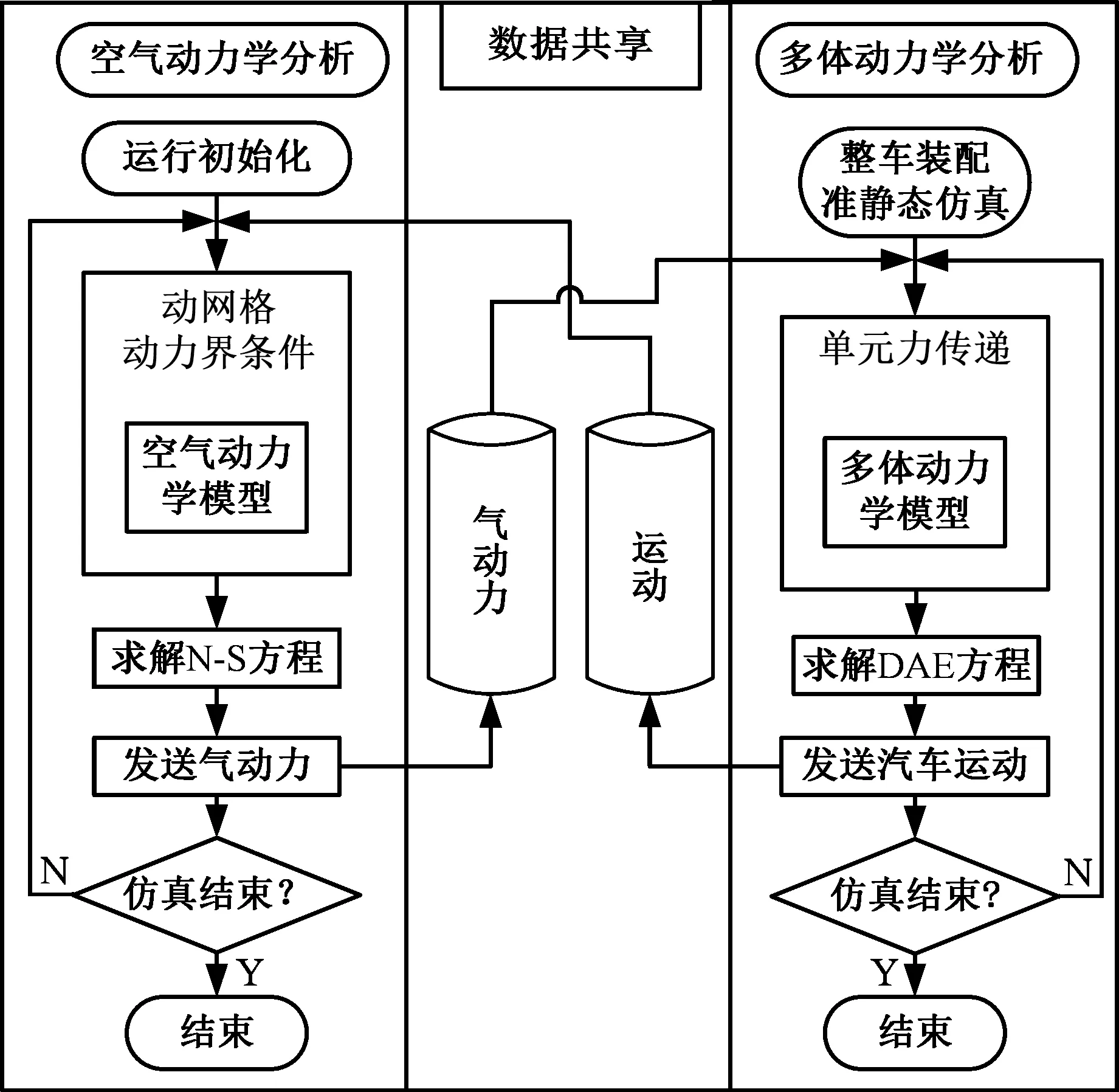
圖8 雙向耦合分析示意圖Fig.8 The diagram for two-way coupling analysis process

雙向耦合分析見圖8，耦合分析同步運行在兩個獨立的計算模型中。在耦合開始前，空氣動力學模型首先進行初始化，并進行2 s的瞬態分析，以使流場波動趨于穩定，同時多體動力學模型也進行準靜態仿真，在無氣動力作用下運動2 s。初始仿真之后，空氣動力學模型與多體系統動力學模型進行初始數據交換。空氣動力學模型中的車身接收到運動數據，求解運動網格方程，重新計算生成新網格，并進行一個步長的CFD仿真，在每一步仿真結束后，空氣動力學模型發送數據到耦合服務器。同樣地，多體系統動力學模型在接收到氣動力后，在氣動力的作用下進行動力學求解，并在每一步的仿真結束時發送質心位置運動參數，最終兩個模型得以實時同步耦合，在耦合持續0.5 s之后，空氣動力學模型中的自然側風或動邊界側風開始起作用，汽車在側風下的氣動力被傳遞給多體動力學模型，多體動力學模型中的車身在氣動力的作用下發生側滑、側傾、橫擺、俯仰等運動，同時空氣動力學模型中的車身通過ALE方法發生運動，汽車在不同姿態下的瞬態流場變化得到求解，最后仿真在耦合持續3 s之后結束。從該耦合過程可以看出，該耦合方法既考慮了汽車各個總成結構對運動求解的影響，同時也考慮了姿態變化對流場求解的影響。

2 結果驗證和分析

2.1 空氣動力學模型風洞試驗驗證

由于側風道路試驗的危險性和困難性，本文瞬態模擬方法的驗證采用風洞試驗的方法。在湖南大學HD-2風洞進行風洞測力和粒子圖像測速(PIV)試驗，該風洞高速試驗段長17 m、寬3 m、高2.5 m，最大允許試驗風速58 m/s，速度不均勻性大于±0.1%，紊流度大于±0.2%，高速試驗段的軸向靜壓梯度在風速30 m/s時為0.000 16/m、風速45 m/s時為0.000 11/m,方向的不均勻性Δαi≤0.5°、Δβi≤0.5°。氣動力的測量采用六分量浮框式應變天平，試驗模型采用與仿真1∶3的縮比模型，主流風速為100 km/h，與仿真車速相同。在縮比模型風洞試驗中，只要滿足了雷諾數的近似，試驗結果的精確度就是足夠的[1]。而若要使風洞中的縮比模型與仿真1∶1模型雷諾數相等，計算得到的試驗風速就需達到300 km/h，由于風速的提高受壓縮比和動力限制，因此實現完全的雷諾數相似是不可能的，但研究表明雷諾數存在一個自準區，當模型試驗的雷諾數超過某個數值時，雷諾數對流動特性的影響較小，雷諾數近似就可以實現[25]，其中美國汽車工程學會推薦該值為0.7×106，日本專家推薦該值為0.5×106，本文1∶3縮比模型的雷諾數為2.9×106，該雷諾數達到了自準區，認為該縮比模型風洞試驗結果可靠，可以用于空氣動力學仿真模型的驗證。風洞試驗現場見圖9。

(a)測力試驗 (b)PIV試驗圖9 風洞試驗現場Fig.9 Wind tunnel test

風洞試驗測力結果表明，該車氣動阻力系數為0.284，氣動升力系數為-0.047，通過網格無關性驗證，方案3和方案4的網格與試驗最接近，氣動阻力系數誤差為0.4%，氣動升力系數誤差為2.1%，方案4相較于方案3，網格數量雖然增加了，但氣動力系數保持不變，這可能是因為在風洞中進行試驗時，環境溫度的測量誤差和試驗儀器的累計誤差等原因，導致試驗結果與仿真結果的誤差一直存在，但該結果誤差較小，在允許范圍內。在橫擺角0°、風速30 m/s的工況下，進行汽車尾部PIV試驗，試驗結果見圖10，可以看到在尾部均形成了兩個渦，上部為順時針渦，下部受底部氣流影響，行成一個逆時針渦。與試驗相比，LES結果中上部渦結構更大，下部的渦大小相近，這是由于PIV試驗中，汽車尾部區域的選擇偏差可能導致汽車尾部流場結構的捕捉不足。PIV中下部位置的渦靠近地面位置的流線曲率較大，而仿真工況下相對較小，這是因為PIV中粒子在車身表面和壁面沉降較為嚴重，導致壁面附近的流速比仿真工況下更低，而遠離位置比較準確，因此形成較大的彎折，但總體上認為，仿真結果與試驗結果相近，證明了本文選擇的LES數值模擬方法的可行性。

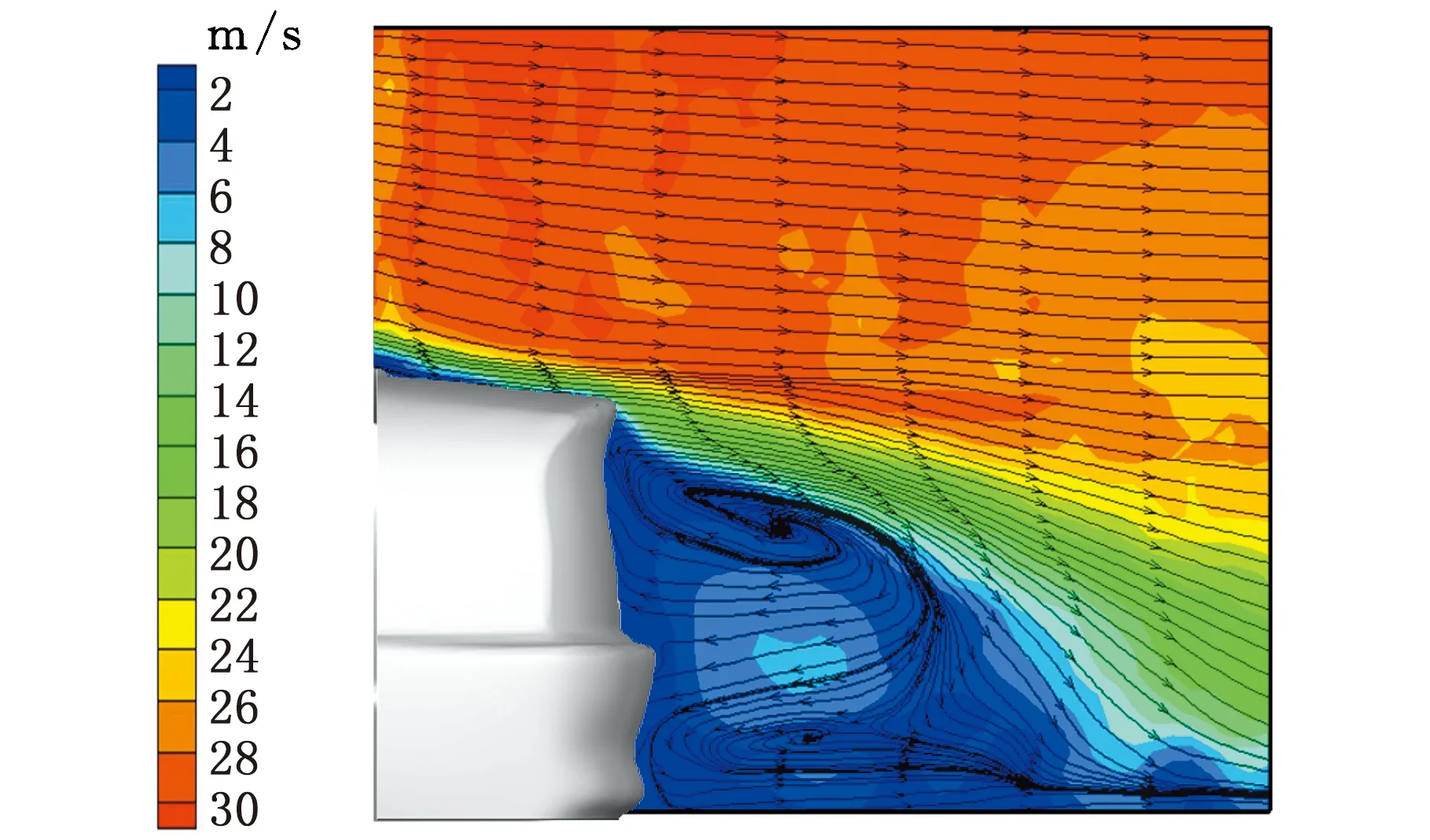
(a)PIV試驗結果

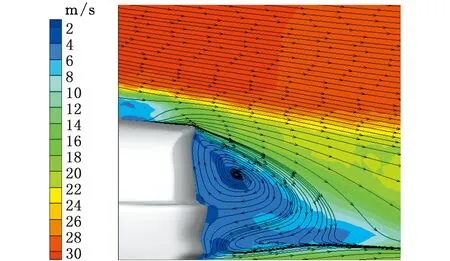
(b)LES模擬結果圖10 汽車尾部流場對比Fig.10 The comparison of vehicle tail flow fluid

2.2 汽車多體動力學模型魯棒性驗證

對于汽車多體系統動力學模型魯棒性的驗證，通過改變風壓中心的位置驗證汽車動力學模型捕捉已知運動的能力。在汽車多體系統動力學模型中的質心位置施加一恒定側向力，根據風壓中心的定義[22]，該側向氣動力的作用點可以看作為風壓中心。標準風壓中心位置(CPstd)位于距離汽車前軸44%的位置。使風壓中心從標準位置分別向前(CPfwd)和向后(CPbwd)，以及向上(CPuwd)和向下(CPdwd)移動兩步，每步移動150 mm，分析汽車捕捉側偏運動和側傾運動的能力，仿真結果如圖11所示。

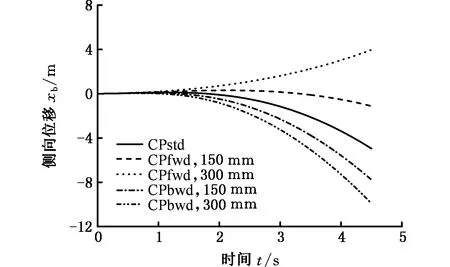
(a)風壓中心前后移動

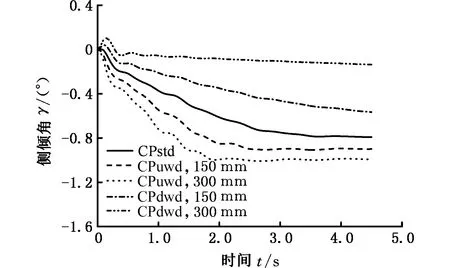
(b)風壓中心上下移動圖11 風壓中心移動對汽車運動影響Fig.11 The impact analysis of the moving of CP on vehicle motion

由圖11a可以看出，當風壓中心在標準位置時，汽車向側向反向偏移，這是因為側向力導致汽車產生一個正的橫擺力矩，汽車在橫擺力矩的作用下向左側運動，從而導致反向的側偏位移；當風壓中心向后移動時，距離越遠，正的橫擺力矩越大，汽車的側向位移越大；當風壓中心前移時，汽車側向偏移減小，但向更遠的位置移動時，汽車向正向偏移。這表明汽車能捕捉OXY平面的運動趨勢。

由圖11b可以看出，當風壓中心向上移動時，產生一個負的側傾力矩，且風壓中心越高，汽車受到的側傾力矩越大，汽車在側向力和側傾力矩共同的作用下產生的側傾角也越大；當風壓中心位于質心下側時，產生一個正的側傾力矩，且風壓中心位置越低，汽車受到的側傾力矩越大，其抵抗側向力的作用越大，汽車在側傾力矩和側向力的共同作用下側傾角也越小，這也是汽車的風壓中心要盡量低的原因。這表明汽車能捕捉OYZ平面的運動變化。

汽車在側向力的作用下，車身運動能較好地被捕捉，因此該汽車多體系統動力學模型的魯棒性較好，適合本文的側風穩定性研究。

2.3 汽車單雙向耦合差異分析

根據ISO分析工況，采用動態邊界方法模擬標準側風，對該汽車進行了單向耦合(1 way)和雙向耦合(2 way)數值模擬，計算結果如圖12所示。其中，Cd、Cs、Cl和Crm、Cpm、Cym分別表示阻力系數、側向力系數、升力系數和側傾力矩系數、俯仰力矩系數、橫擺力矩系數；Dy、Dz和Ra、Pa、Ya分別表示側向位移、垂向位移和側傾角、俯仰角、橫擺角。

從圖12a可以看出，汽車側向力系數和阻力系數的單雙向耦合的結果差異不大，因此汽車側向位移差異也不大。在3.5～4.0 s之間，單向耦合的橫擺力矩比雙向耦合的橫擺力矩大，因此單向耦合的汽車橫擺角也大于雙向耦合結果。在3.25～4.0 s之間，單向耦合的汽車側傾力矩略大于雙向耦合的結果，因此汽車的側傾角的波動幅值也較大。氣動升力在仿真過程中出現了較大的差異，因此氣動俯仰力矩也產生了較大的差異，但由于汽車受重力作用，氣動升力對汽車垂向位移的貢獻較小，波動相對較小，俯仰角也就較小。這也說明，氣動升力和橫擺力矩對汽車車身姿態的變化更加敏感。

圖13為3.5 s和4.0 s時刻汽車車身表面壓力云圖，可以看出，在迎風側汽車表面壓力差異不大，然而在背風側壓力差別較大，在總體趨勢上，雙向耦合的背風側壓力略高，特別是在尾部和C柱區域，這也是側傾力矩和橫擺力矩差異比較明顯的原因。

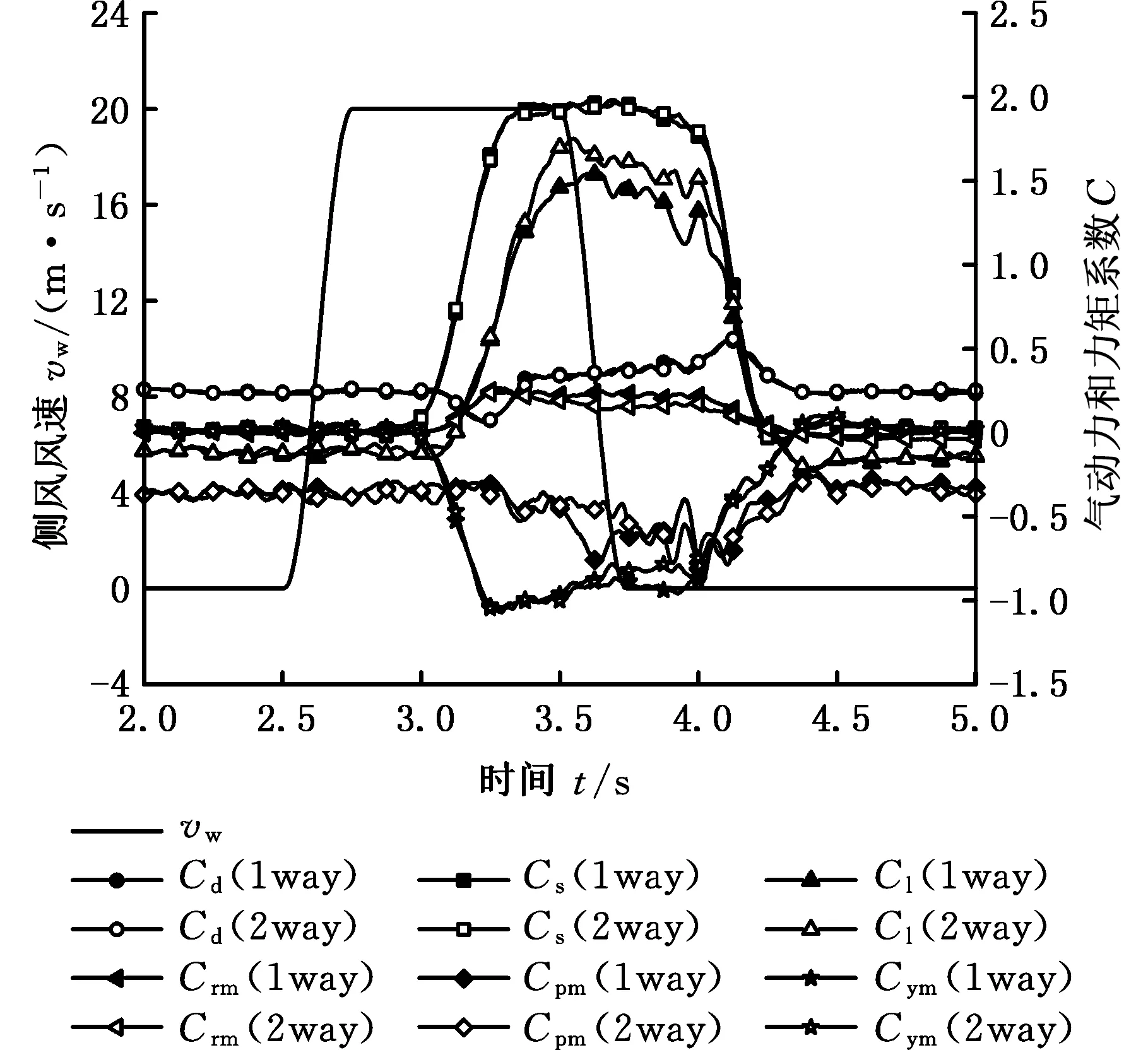
(a)單雙向耦合氣動力系數對比

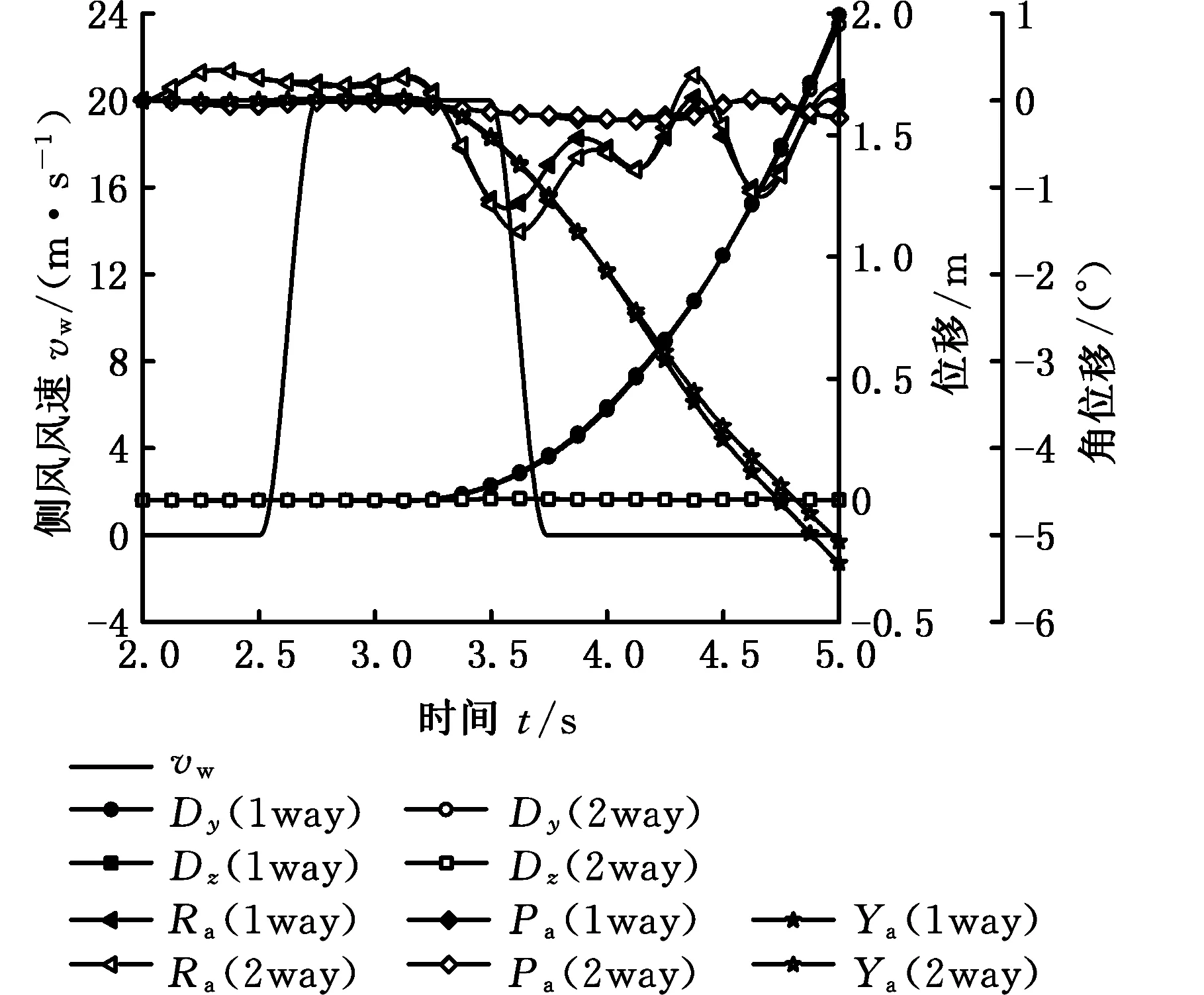
(b)單雙向耦合汽車位移變化對比圖12 ISO工況下單雙向耦合結果對比Fig.12 The comparison of results of one-way coupling and two-way coupling under ISO condition

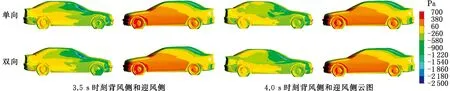
圖13 3.5 s和4.0 s時刻汽車側面壓力云圖Fig.13 The pressure contour on vehicle both sides at t=3.5 s and t=4.0 s

3.5 s時刻的汽車頂部和底部壓力云圖見圖14，在汽車頂部和迎風側的A柱均出現了較大的正壓區域，而在背風側的A柱出現氣流的分離，單雙向耦合的差異并不明顯。在汽車的底部，很明顯地可以觀察到前部迎風側車輪產生的氣流分離導致的負壓區域，相較于單向耦合結果，雙向耦合的負壓區域較小，這是由于雙向耦合中汽車發生了側傾運動，汽車底部流入了更大的氣流，底部壓力升高。此外，背風側的前后車輪處均產生了較大的壓力集中，且雙向耦合中，由于更大的底部氣流，這種現象也更加明顯，因此在車輪處產生了更大的壓力，圖12中的側傾運動與升力變化的單雙向耦合差異也較大，由此可知有必要采用雙向耦合分析方法研究汽車運動對氣動力的影響。

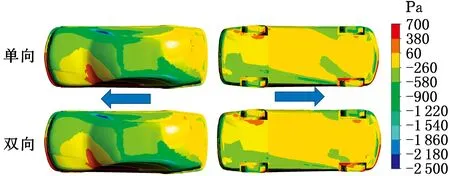
圖14 3.5 s時刻汽車頂部與底部壓力云圖Fig.14 The pressure contour on vehicle top and bottom at t=3.5 s

2.4 側風形式對汽車側風穩定性影響研究

以瞬態邊界和動態邊界方法分別對汽車的側風穩定性進行雙向耦合仿真，汽車在遭遇側風影響時的速度云圖見圖15，可以看到在自然側風的工況中，在3.0 s時，汽車已經完全進入側風區域，并且風速達到最大，這是由于側風從2.5 s開始施加于前側和左側入口，3.0 s時刻側風邊界條件已經達到了最大值，并且已經運動到車身位置，在3.5 s時側風風速開始降低，但側風的作用并沒有消失，汽車仍舊受側風的影響，4.0 s時，側風風速逐漸降低，在4.5 s時，汽車完全退出側風作用區域，5.0 s時，側風完全消失。標準側風則完全不同，可以看到，雖然側風邊界條件從2.5 s時就開始起作用，但直到3.0 s前后時，汽車頭部才最先接觸到側風，并且風速逐漸增加到最大，在3.5 s時，汽車已經完全進入側風區域，從4.0 s時，汽車開始退出側風區，最終4.5 s時汽車完全穿過側風區域，在5.0 s時側風消失。這表明自然側風對汽車的影響更加迅速，并且側風對汽車的作用是全局的，整個車身側面同時受到側風影響；而標準側風的影響是緩慢地從車頭到車尾逐漸受影響。

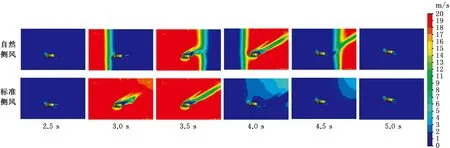
圖15 汽車遭遇兩種不同側風時的側向速度云圖Fig.15 Velocity contour in Y direction when vehicle come across two different crosswind

上述兩種工況下，汽車的氣動力系數時間曲線如圖16所示，可以看出，在自然側風作用下的汽車氣動力系數均比標準側風下的要早0.5 s，這正是由于自然側風作用于全局，使得側風幾乎沒有任何延遲地作用到車身。此外，自然側風的阻力系數Cd在側風風速達到最大加速度值的時刻出現了一個較大的峰值，此后又減小并穩定，而標準側風的阻力系數并沒有出現峰值，而是逐漸地增大并穩定。這是因為自然側風迅速地在全區域增加的時候，流場還未穩定，左側壓力較高，而右側較低，從而導致較大的壓差側向力，與此相同，當自然側風風速降低并消失時同樣出現了一個峰值，這是因為汽車背風面的側風依舊存在，而迎風面的側風已經開始下降并消失，不穩定的流場因此導致一個較大的負壓。對于標準側風工況，由于側風區域逐漸靠近車身，汽車車身受到的側向力逐漸增加，左右兩側的側風基本上同時向后方移動，因此并沒有出現自然側風工況下的峰值。

圖16 不同側風下汽車氣動力系數變化曲線Fig.16 The variation of aerodynamic force coefficients in two different crosswind

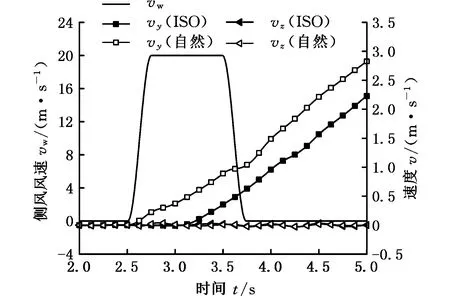
(a)汽車運動速度

(b)汽車運動角速度圖17 不同側風下汽車運動速度變化曲線Fig.17 The variation of vehicle velocity in two different crosswind

圖17描述了汽車在多體系統動力學模型中的汽車運動速度。圖中，vy與vz分別表示汽車的側向速度和垂向速度；Rr、Pr與Yr分別表示汽車的側傾角速度、俯仰角速度及橫擺角速度。由圖17a可以發現，在自然側風下，自側風開始的瞬間起，汽車的速度便急速增大，而標準側風的工況中，汽車在側風開始后的0.5 s開始運動。可以看到自然側風作用下的汽車側向速度曲線出現兩次轉折，標準側風工況下的汽車側向速度曲線相對平滑。在側風消失后，汽車依舊具有側向的偏移速度，這是因為汽車的方向發生了橫擺之后，汽車的縱向運動速度沿Y軸的分量依然存在，因此汽車的側向偏移速度沒有因為側風的消失而降低。汽車的垂向運動速度較小，且一直處于波動狀態，但可以看出自然側風工況下汽車的垂向運動速度更大，波動更劇烈。由圖17b可以發現，在自然側風作用下，側風開始時，汽車的側傾角迅速產生較大的波動，而在側風消失時也產生了較大的反向側傾角速度波動。側風接觸汽車時，在自然側風下的汽車側傾角速度大于標準側風下的側傾角速度，而標準下的側傾角速度變化周期大于汽車在自然側風下的變化周期，這也表明汽車在自然側風作用下的運動變化更劇烈。而在側風離開汽車時，標準側風作用下的汽車側傾角速度大于自然側風作用下的側傾角速度，這主要是因為汽車的側傾受到懸架結構的影響，自然側風下的汽車側傾角小，懸架對車身的作用也較小，而標準側風下的汽車側傾角較大，車身受懸架影響也較大，具體的側傾角位移變化如圖18所示。對于汽車的俯仰運動，在自然側風環境中，汽車的俯仰角速度變化也較標準側風更加劇烈，但兩種工況下的角速度峰值基本相同。對于汽車的橫擺運動，可以看出，無論在哪種環境中，在側風作用期間，汽車的橫擺角速度都逐漸增大，當側風降低至消失后，汽車的橫擺角度都有略微的降低，但并沒有趨向于零，從而導致汽車的橫擺角逐漸增大。

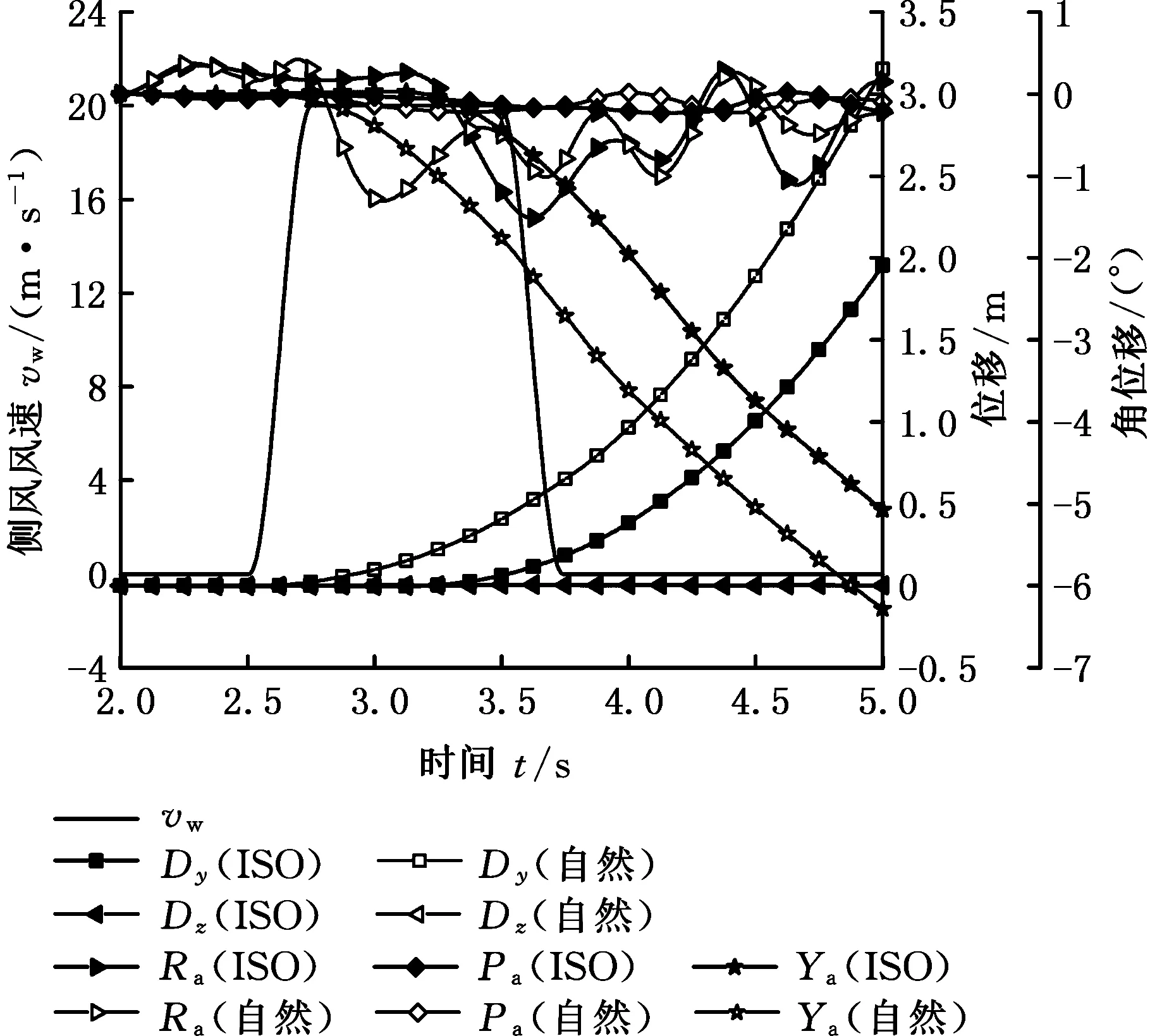
圖18 不同側風下汽車位移變化曲線Fig.18 The variation of vehicle displacement in two different crosswind

標準側風和自然側風兩種工況下汽車的運動位移如圖18所示。按照ISO標準，汽車在側風的作用下，從2.5 s開始至4.5 s時，標準側風和自然側風下的汽車側向位移分別為1.01 m和1.89 m，而在本文的仿真結束的5.0 s時，汽車的側向位移達到1.96 m和3.15 m。這兩種工況下的汽車側偏位移均在標準中的5 m的范圍內，但是根據文獻[26]，在中國的高速公路上，汽車側偏達到0.975 m就已經非常危險了，所以汽車在2 s內的位移偏移依舊過大，直接影響了汽車的行駛安全性，而且自然側風對汽車的影響更大，標準中對汽車側偏位移的評價略顯不足。除此之外，汽車的橫擺角變化也非常大，標準側風作用下汽車的橫擺角在2 s內達到了1.96°，而自然側風下的橫擺角更大，為3.62°。圖17中汽車的橫擺角速度雖然都在減小，但是并沒有降低為零，因此汽車在后續的0.5 s內繼續側偏，在0.5 s內橫擺角分別增加了3.11°和2.66°。這是因為標準側風相對于自然側風存在0.5s的時間滯后，但即便考慮到標準側風的滯后，它對汽車橫擺角變化的影響依舊小于自然側風。對于汽車的側傾角變化曲線，可以看到，在側風作用開始時，雖然自然側風作用下的汽車側傾角速度較大，但其側傾角小于標準側風作用下的側傾角，這主要是因為此時汽車在標準側風作用下的角速度變化周期較長，而自然側風作用下的汽車角速度變化周期較短。在側風作用期間汽車的側傾角一直在小于零的位置波動，這是由于汽車的側傾角變化受側傾力矩和懸架作用的共同影響。在側風消失時，汽車在穩態自然側風下的側傾角波動依舊小于零，而標準側風作用下的汽車側傾角出現了反向的波動，這主要是因為此時汽車受到的氣動力與懸架作用方向一致的原因，這也進一步說明了采用雙向耦合分析方法的必要性。同時，這也導致了圖17b中，在4.5 s時汽車的側傾角速度出現了較大的反向波動。

綜上結果表明，自然側風下汽車的氣動力作用更加迅速，對汽車周圍流場的影響也更大，特別是在側風加速和減速期間，流場更加不穩定，汽車的運動也因此相較于標準側風更加劇烈，而標準試驗中的標準側風對汽車穩定性的評價稍顯不足，對于國內汽車的側風穩定性的評價，需要根據國內道路情況進行考慮。

3 結論

(1)汽車在標準側風的作用下會發生瞬態的姿態變化，而汽車的姿態變化會反過來影響汽車周圍的流場，對汽車側風穩定性的研究需要考慮汽車車身運動與流場變化的實時耦合。

(2)汽車在側風環境下的運動受側風和懸架的共同影響，當側風作用與懸架作用方向一致時，汽車的運動會受到較大的影響。

(3)自然側風下的流場是全局瞬態的，比標準側風下的流場更加不穩定，對汽車的氣動六分力的影響更劇烈，對汽車的運動的影響也更大，汽車側風穩定性的試驗和仿真研究不能局限于標準側風試驗工況。