電導(dǎo)率線性變化直流電測深三維有限單元法正演模擬

歐東新,王 超,閆凱暄,馮 歡

(1.桂林理工大學(xué) a.廣西隱伏金屬礦產(chǎn)勘查重點(diǎn)實(shí)驗(yàn)室;b.地球科學(xué)學(xué)院,廣西 桂林 541006;2.中國有色桂林礦產(chǎn)地質(zhì)研究院有限公司,廣西 桂林 541004)

0 引 言

三維直流電測深的正演是進(jìn)行復(fù)雜地電模型勘探資料反演的基礎(chǔ),主要采用有限單元法、邊界單元法、積分方程法、有限差分法等方法。Xu等[1]利用邊界單元法進(jìn)行了起伏地形三維電阻率法的正演模擬。Zhang等[2]利用共軛梯度法進(jìn)行了三維電阻率法的有限差分正演模擬和反演。底青云等[3]利用積分方程法進(jìn)行了三維電阻率成像的研究。 Li等[4]利用不完全共軛梯度法進(jìn)行了有限單元法三維直流電阻率法的正演模擬,并與有限差分法對比,得出當(dāng)模型電阻率差異較大時(shí),有限單元法計(jì)算精度優(yōu)于有限差分法的結(jié)論。黃俊革[5]用有限單元法對電導(dǎo)率、極化率分塊均勻的地下介質(zhì)進(jìn)行了正反演研究。吳小平等[6]采用對稱超松弛預(yù)條件共軛梯度(SSOR-PCG)迭代算法求解三維電阻率有限元法形成的大型線性方程組。 Rücker等[7]進(jìn)行了三維電阻率有限單元法正演,采用異常電位法計(jì)算,著重于網(wǎng)格剖分、正常電位的計(jì)算以及直接法與迭代法解方程的對比；在計(jì)算起伏地形正常電位時(shí),在電源點(diǎn)附近局部加密網(wǎng)格,采用二次形函數(shù)對電位插值。呂玉增[8]采用有限單元法進(jìn)行了地-井、井-地激發(fā)極化法三維快速正反演研究，利用改進(jìn)的稀疏矩陣MSR(modified sparse row)存儲方法存儲系數(shù)矩陣, 采用SSOR-PCG迭代算法求解大型線性方程組。 任政勇等[9]利用非結(jié)構(gòu)化網(wǎng)格進(jìn)行了三維直流電阻率有限單元法正演模擬。 李長偉[10]采用Krylov子空間預(yù)條件共軛梯度法(PCG)解三維電阻率有限元法形成的大型線性方程組。

以上直流電測深三維正演都是電導(dǎo)率分塊均勻的，而野外的地電分布一般是連續(xù)變化的，尤其是地下水的電導(dǎo)率與礦化度成正比，因此有必要研究電性參數(shù)連續(xù)變化的正演模擬方法。阮百堯等進(jìn)行了電導(dǎo)率線性變化的二維地電斷面電阻率法有限單元法正演模擬[11], 并進(jìn)行了水平大地電導(dǎo)率線性變化電阻率法三維有限單元法正演[12],采用了非齊次邊界條件、異常電位法進(jìn)行模擬,但是沒有提到用何種方法進(jìn)行線性方程組的求解,根據(jù)文中計(jì)算時(shí)間較長推測，應(yīng)該是采用直接解法。劉海飛等[13]進(jìn)行了起伏地形電導(dǎo)率連續(xù)變化的三維激電數(shù)據(jù)有限元數(shù)值模擬,采用非齊次邊界條件,四面體單元剖分,單元內(nèi)電導(dǎo)率線性變化,由于采用總電位法,在電源點(diǎn)附近誤差較大。劉海飛等[14]利用異常電位法進(jìn)行了電導(dǎo)率線性變化的五極縱軸激電測深三維有限元正演模擬,仍然采用非齊次邊界條件。

本文采用與文獻(xiàn)[12]類似的方法進(jìn)行電導(dǎo)率線性變化的直流電測深三維正演模擬,也利用六面體單元剖分模擬水平大地三維地電結(jié)構(gòu);電導(dǎo)率和電位在單元內(nèi)線性變化;采用異常電位法進(jìn)行正演,推導(dǎo)出齊次邊界條件下有限單元法系數(shù)矩陣,令總電位為正常電位和異常電位之和。有限元法計(jì)算的是異常電位,與點(diǎn)源水平均勻大地的正常電位相加即可獲得總電位。

與文獻(xiàn)[12]不同之處在于,本文采用齊次邊界條件,這樣有限單元法的系數(shù)矩陣不會(huì)隨著電源點(diǎn)位置的改變而不同,在多個(gè)電極的情況下特別有利。如果采用直接法(如喬累斯基分解法)求解包含多個(gè)不同右端項(xiàng)的線性方程組,一次分解多次回代,可以節(jié)省大量的時(shí)間;如果采用迭代法求解,也有方法能快速求解這種線性方程組[10]。此外，還采用林紹忠[15]改進(jìn)的SSOR PCG迭代算法求解線性方程組,當(dāng)網(wǎng)格節(jié)點(diǎn)較多時(shí),迭代法比直接法計(jì)算速度要快[7]。有限單元法計(jì)算結(jié)果與一維水平層狀電導(dǎo)率線性變化模型濾波算法對比,相對均方差小于0.38%。對二維垂直不連續(xù)分界面模型、均勻大地中的三維低阻體模型也進(jìn)行了電阻率測深正演計(jì)算,驗(yàn)證了本文方法的有效性。

1 三維模型網(wǎng)格剖分

如圖1所示, 計(jì)算區(qū)域?yàn)榇蟮牧骟w, 建立直角坐標(biāo)系,x、y、z在3個(gè)方向進(jìn)行剖分就可以形成結(jié)構(gòu)化六面體單元,與非結(jié)構(gòu)化單元相比, 網(wǎng)格生成簡單, 由于單元排列有規(guī)律, 在計(jì)算網(wǎng)格節(jié)點(diǎn)編號、 有限元存儲矩陣參數(shù)等方面非常省時(shí)。

圖1 六面體單元網(wǎng)格剖分示意圖Fig.1 Skech map of hexahedron mesh

2 變分問題

由文獻(xiàn)[16]得到三維點(diǎn)源電場的異常電位法變分公式

(1)

其中:u為異常電位;σ為電導(dǎo)率;σ′=σ-σ0為異常電導(dǎo)率;σ0為背景電導(dǎo)率;u0為正常電位(即大地電導(dǎo)率全部為σ0的電位);Ω為有限單元法計(jì)算區(qū)域。 本文采用齊次邊界條件, 即在無窮遠(yuǎn)處異常電位為零, 因此式(1)省略了無窮遠(yuǎn)邊界的積分。

3 有限單元法系數(shù)矩陣

對式(1)積分采用六面體單元離散化, 六面體母單元、 子單元如圖2所示, 插值形函數(shù)如式(2)所示[17]。

Ni=(-1)1+ξi+ηi+ζi(ξ+ξi-1)(η+ηi-1)(ζ+ζi-1),i=1,2，…,8。

(2)

單元內(nèi)電導(dǎo)率、 電位利用線性變化形函數(shù)插值

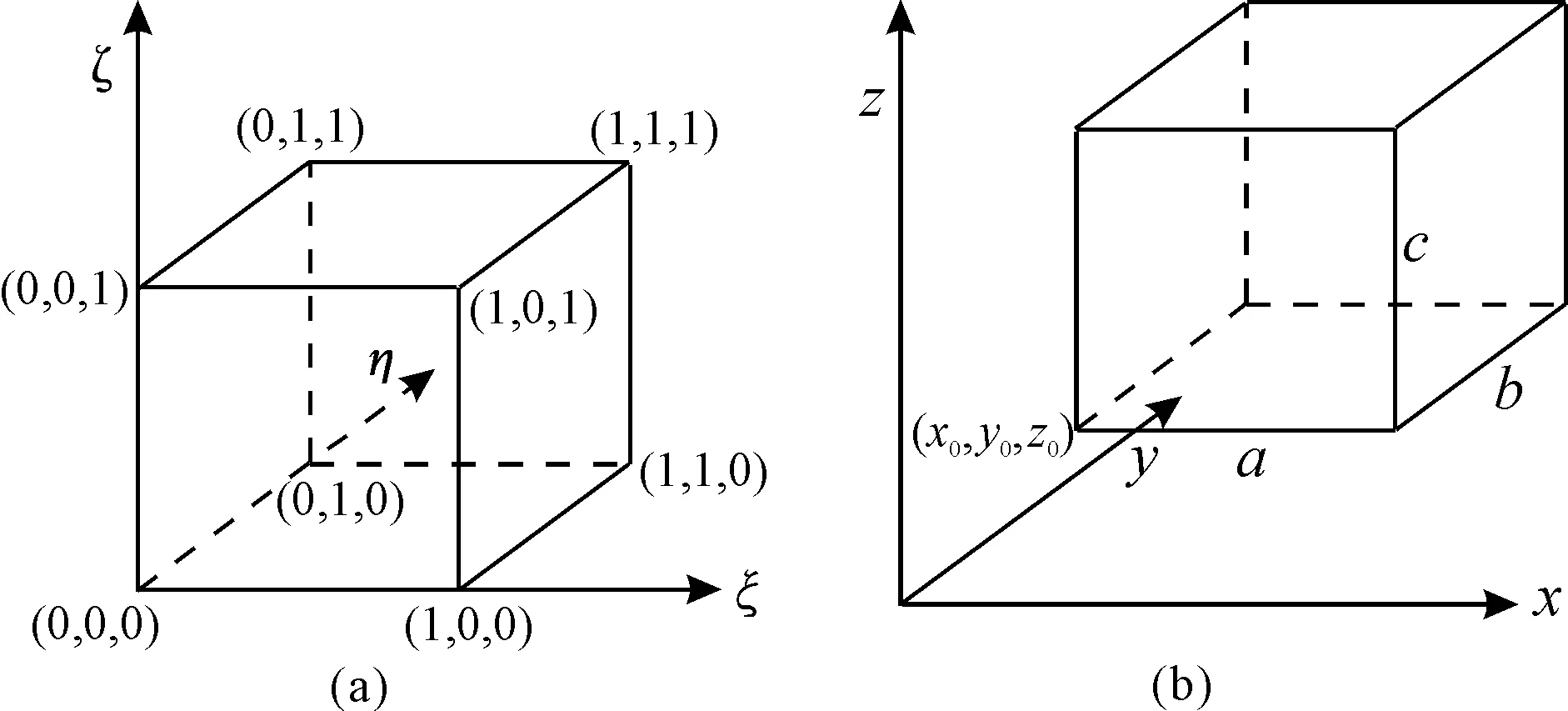
圖2 六面體母單元(a)和子單元(b)Fig.2 Parent element(a) and subelements(b) of hexahedron

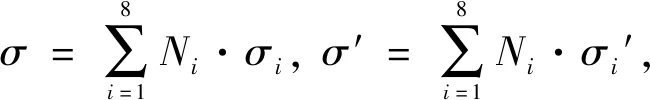
(3)

子單元的坐標(biāo)也線性變化

(4)

將式(1)積分離散為各個(gè)六面體單元積分之和

(5)

利用式(3)對單元積分進(jìn)行插值,得

(6)

其中:ke與ke′為8×8單元系數(shù)矩陣;ue為8個(gè)元素的單元異常電位列向量;u0e為8個(gè)元素的單元正常電位列向量。

由于本文母子單元都是長方體,所以有

x=x0+aξ,y=y0+bη,z=z0+cζ,

(7)

其中:a、b、c為子單元在x、y、z三個(gè)方向的邊長。由式(7)可得

dv=dxdydz=abcdξdηdζ。

(8)

由文獻(xiàn)[16]可得

(9)

其中:J為雅可比變換矩陣。J中的元素可以由式(4)分別對ξ、η、ζ求導(dǎo)獲得。

(10)

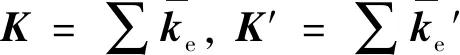
令式(10)變分為零獲得如下線性方程組

(11)

求解式(11)獲得異常電位后與正常電位相加即可獲得總電位,從而求得視電阻率。本文推導(dǎo)了六面體剖分,單元內(nèi)電導(dǎo)率線性變化的單元系數(shù)矩陣ke和ke′：

(12)

其中，kij為8×8單元矩陣ke或ke′的元素;Aij為8×3矩陣;當(dāng)S為單元8個(gè)節(jié)點(diǎn)的電導(dǎo)率向量時(shí), 式(12)計(jì)算的是ke的元素;當(dāng)S為異常電導(dǎo)率向量時(shí), 式(12)計(jì)算的是ke′的元素;α=ab/c;β=ac/b;γ=bc/a;a、b、c為子單元在x、y、z三個(gè)方向的長度。 限于篇幅， 36個(gè)Aij的具體形式未在此列出。

5 線性方程組求解及程序?qū)崿F(xiàn)

式(11)方程組的系數(shù)矩陣為大規(guī)模稀疏矩陣,特別適合用迭代法求解,Rücker等[7]對直接法和迭代法進(jìn)行了對比,發(fā)現(xiàn)在節(jié)點(diǎn)數(shù)較少時(shí)采用直接法計(jì)算速度較快,節(jié)點(diǎn)數(shù)較多時(shí)采用迭代法計(jì)算速度更快,而三維模擬節(jié)點(diǎn)數(shù)一般都在幾萬以上,所以采用迭代法較好。本文采用林紹忠[15]改進(jìn)的SSOR PCG公式編寫了線性方程組的迭代求解程序。將此程序應(yīng)用于筆者以前的正演模擬中[18-19]，在滿足一定精度的條件下，與直接解法相比，計(jì)算速度極大提高。

林紹忠改進(jìn)的SSOR PCG法如下,設(shè)有線性方程組

Ax=b，

(13)

其中：A為對稱正定矩陣, SSOR法的分裂預(yù)處理矩陣為

M=(2-ω)-1(D/ω+L)(D/ω)-1(D/ω+L)T，

(14)

其中：D為A的對角陣；L為A的下三角陣； 0<ω<2為松弛因子。

令

(15)

則

(16)

有改進(jìn)的SSOR PCG迭代格式:

(17)

其中：W是方陣；W-T為W的轉(zhuǎn)置矩陣的逆陣；V為對角陣；g,h,y,d,z,x,b為列向量。

迭代式(17)中需要計(jì)算W-1(zk-Vdk)和W-Tzk+1,在實(shí)際計(jì)算中不需計(jì)算逆陣,而是利用SSOR理論迭代一次就可獲得,以下推導(dǎo)具體的計(jì)算公式。

由式(14)和式(15)可得

M=WV-1WT，

(18)

M-1=W-TVW-1。

(19)

對式(19)兩邊左乘(W-TV)-1可得

W-1=V-1WTM-1，

(20)

因此，W-1與任意列向量b的乘積為

W-1b=V-1WTM-1b。

(21)

根據(jù)SSOR理論[20],對于線性方程組(13)有

M-1b=xk+1-Bxk，

(22)

其中：B=(D/ω+U)-1[(1/ω-1)D-L](D/ω+L)-1[(1/ω-1)D-U];U為L的轉(zhuǎn)置矩陣,即上三角陣。 只要令xk=0, 按照SSOR公式迭代一次算出xk+1即M-1b。 因此只需令b=(zk-Vdk), 先用SSOR迭代一次算出M-1(zk-Vdk), 然后利用式(21)即可獲得W-1(zk-Vdk)。

下面推導(dǎo)W-Tzk+1的計(jì)算公式,式(19)兩邊右乘(VW-1)-1可得:

W-T=M-1WV-1，

(23)

W-Tzk+1=M-1WV-1zk+1。

(24)

同樣進(jìn)行一次SSOR迭代就能求出式(24)。

為了減少存儲占用, 對系數(shù)矩陣進(jìn)行CSR(行壓縮的稀疏存儲)存儲,只存非零元素。 由于采用結(jié)構(gòu)化六面體網(wǎng)格,網(wǎng)格編號有規(guī)律, CSR的壓縮矩陣指示參數(shù)的計(jì)算非常快速, 47 068個(gè)節(jié)點(diǎn)用時(shí)10-2s以下, 而用非結(jié)構(gòu)化網(wǎng)格方法計(jì)算壓縮矩陣指示參數(shù)用時(shí)30 s。 根據(jù)Rücker等[7]的研究, 只要迭代法的殘差小于10-6, 求解精度就可以滿足勘探的要求, 本文也采用這個(gè)精度標(biāo)準(zhǔn)。 由于相鄰電極供電時(shí)的電位分布特征接近, 第1個(gè)電極供電的初始解設(shè)為0, 此后所有電極的初始解采用上一個(gè)電極供電所計(jì)算出來的電位平移到當(dāng)前電極供電時(shí)的相應(yīng)節(jié)點(diǎn)位置上作為初始解, 這樣求解的迭代次數(shù)能減小很多。 例如對模型2進(jìn)行21個(gè)電極的高密度α裝置的視電阻率測深數(shù)據(jù)正演, 192 892個(gè)節(jié)點(diǎn), 第1個(gè)電極供電時(shí), 電位初始值設(shè)為0,迭代次數(shù)為130次, 而其他電極采用上一個(gè)電極供電所計(jì)算出來的電位平移到當(dāng)前電極供電時(shí)的相應(yīng)節(jié)點(diǎn)位置上作為初始解, 迭代次數(shù)最多為84次, 最少為23次, 平均為34次。

由于每個(gè)電極供電都可獨(dú)立計(jì)算,所以可以采用并行方法。本文采用PGI Fortran 編程,利用OpenMP 編譯指令對程序進(jìn)行并行化，在雙核2.7 GHz筆記本上進(jìn)行計(jì)算，采用并行指令的計(jì)算速度基本為串行的2倍。

5 算 例

5.1 一維水平層狀電導(dǎo)率線性變化模型(模型1)

首先利用一維水平層狀電導(dǎo)率線性變化模型(模型1， 圖3)，對稱四極測深數(shù)據(jù)來檢驗(yàn)本文方法的準(zhǔn)確性。模型1為3層模型,第1層厚度5 m,電阻率為10 Ωm(電導(dǎo)率為0.1 S/m); 第2層厚度5 m, 電導(dǎo)率從0.1 S/m線性變化到0.01 S/m(電阻率為100 Ωm)。本文用文獻(xiàn)[21]水平層狀大地的計(jì)算方法來模擬電導(dǎo)率線性變化的模型，將第2層過渡層用多個(gè)均勻薄層來近似，用120個(gè)系數(shù)[22]的濾波算法進(jìn)行計(jì)算。編制程序?qū)^渡層不斷細(xì)分,直到前后兩次細(xì)分模型的視電阻率相對均方差小于0.001%時(shí)終止分層,所得結(jié)果作為電導(dǎo)率線性變化模型的理論值。

對模型1的有限單元法網(wǎng)格剖分如表1所示。

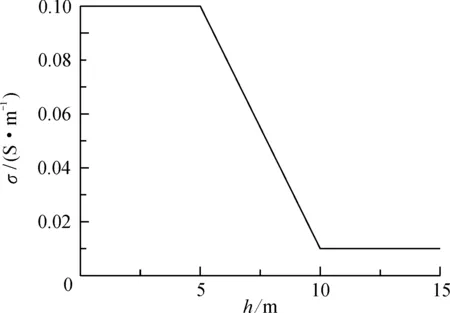
圖3 一維水平層狀電導(dǎo)率線性變化模型(模型1)Fig.3 1D layered model with linear variable conductivity (Model 1)

坐標(biāo)節(jié)點(diǎn)值/mx-10230,-5110,-2550,-1270,-630,-310,-150,-70,-30,-10,0,10,20,30,40,50,60,70,80,90,100,110,120,130,140,150,160,170,180,190,200,210,230,270,350,510,830,1470,2750,5310,10430y-10230,-5110,-2550,-1270,-630,-310,-150,-70,-30,-10,0,10,20,30,40,50,60,70,80,90,100,110,120,130,140,150,160,170,180,190,200,210,230,270,350,510,830,1470,2750,5310,10430z0,0.5,1,2,3,4,5,10,15,20,25,30,35,40,45,50,60,75,100,150,200,300,450,750,1300,2500,4500,8500

節(jié)點(diǎn)個(gè)數(shù)為41×41×28=47 068。 線性方程組系數(shù)矩陣的上三角部分CSR方式存儲元素為623 815個(gè)。 在x方向布置測線, 共21個(gè)電極, 電極距10 m,計(jì)算了α裝置的視電阻率測深數(shù)據(jù)。21個(gè)電極的高密度測深有限元計(jì)算用時(shí)為12.5 s。阮百堯等[12]的方法計(jì)算一條測深曲線用時(shí)1 825 s,如果只是為了計(jì)算一條測深曲線,就可以利用互換定理,將電源點(diǎn)放在M、N電極,而測量點(diǎn)放在A、B電極,這樣利用喬累斯基分解就只需對方程組系數(shù)矩陣進(jìn)行一次分解,而回代的時(shí)間很少,因此1 825 s基本上是解一次線性方程組的時(shí)間。為了對比直接法和迭代法在三維電測深正演模擬中的效率,采用表1中的網(wǎng)格參數(shù)和21個(gè)電極分別用直接法(喬累斯基分解法)和本文迭代法對模型1進(jìn)行了α裝置高密度正演計(jì)算。本文迭代法所用時(shí)間12.5 s， 而直接法用時(shí)110.6 s。對于更多節(jié)點(diǎn)的模型也進(jìn)行了計(jì)算,隨著節(jié)點(diǎn)數(shù)的增加,直接法用時(shí)急劇增加,而迭代法用時(shí)增加相對要慢一些。因此可以看出，對于三維模型,在節(jié)點(diǎn)數(shù)巨大的情況,迭代法比直接法快得多,這與文獻(xiàn)[7]的結(jié)論相同。此外還要注意到本文采用的是齊次邊界條件,有限單元法的系數(shù)矩陣不會(huì)隨著電源點(diǎn)位置不同而不同,因此直接法只用一次分解,其他電源點(diǎn)的計(jì)算只需回代即可。而阮百堯等[12]采用的是非齊次邊界條件,這樣每個(gè)電源點(diǎn)形成的線性方程組都要重新分解,用時(shí)將會(huì)是巨大的。

理論及有限元視電阻率數(shù)據(jù)如表2所示。 理論值1個(gè)極距只計(jì)算1個(gè)值, 而本文有限元采用高密度方式采集數(shù)據(jù), 每個(gè)極距有多個(gè)數(shù)據(jù), 表2中給出了最小值和最大值, 以及它們與理論值的相對均方差。 在不同極距下,本文有限元計(jì)算值與理論值的相對均方差均小于0.38%。

正如濾波算法一樣,如果用電導(dǎo)率分塊均勻的有限單元法程序來模擬模型1中電導(dǎo)率線性變化的地電模型，需要剖分得更密才行,而從表1中z方向節(jié)點(diǎn)坐標(biāo)可知,本文方法只用2個(gè)節(jié)點(diǎn)就能模擬電導(dǎo)率線性變化地層。

模型1理論及有限元視電阻率測深曲線如圖4所示，“+”為本文有限元計(jì)算值(FEM)(表2中最小值)，可見計(jì)算值與理論值擬合較好。

表2 模型1的理論及有限單元法視電阻率

圖4 模型1理論及有限單元法視電阻率測深曲線Fig.4 Apparent resistivity sounding curves of theory and FEM of Model 1

5.2 垂直不連續(xù)分界面模型(模型2)

本文方法也可以模擬電導(dǎo)率分塊均勻的地電模型,只要令單元8個(gè)節(jié)點(diǎn)的電導(dǎo)率相同即可。利用2D垂直不連續(xù)分界面模型(模型2,圖5)測試本文程序?qū)M向電性突變的計(jì)算精度。分界面左邊為100 Ωm,右邊為200 Ωm。垂直于分界面布置一條100 m長的測線,21個(gè)電極,電極距5 m,界面位于50 m處。利用鏡像法計(jì)算高密度α裝置視電阻率解析解。本文異常電位有限單元法模型的背景電阻率取分界面兩側(cè)的平均值150 Ωm,網(wǎng)格x、y方向節(jié)點(diǎn)數(shù)為83,z方向節(jié)點(diǎn)數(shù)為28,總節(jié)點(diǎn)數(shù)為192 892,電極間插入2個(gè)節(jié)點(diǎn),計(jì)算用時(shí)49.56 s。有限單元法視電阻率與解析解的相對均方差為0.058%,最大相對誤差為1.996%,出現(xiàn)在垂直分界面附近。

圖6為有限元計(jì)算的對稱四極剖面與理論值對比,AO為7.5 m,MN為5 m。理論對稱四極視電阻率剖面曲線(實(shí)線)在從高阻體進(jìn)入低阻體前會(huì)先有個(gè)小的下降再上升，然后再下降;從高阻體進(jìn)入低阻體后,視電阻率有小的上升, 然后又較快地減少到低阻體的電阻率值。這些視電阻率的曲線特征與程志平[21]的垂直分界面的對稱四極剖面曲線特征基本類似,但也有所不同。不同之處在于本文的測量電極MN為5 m,而文獻(xiàn)[21]的MN為0。因此，文獻(xiàn)[21]的曲線在垂直界面處突變,而本文理論曲線在界面處不是突變的。

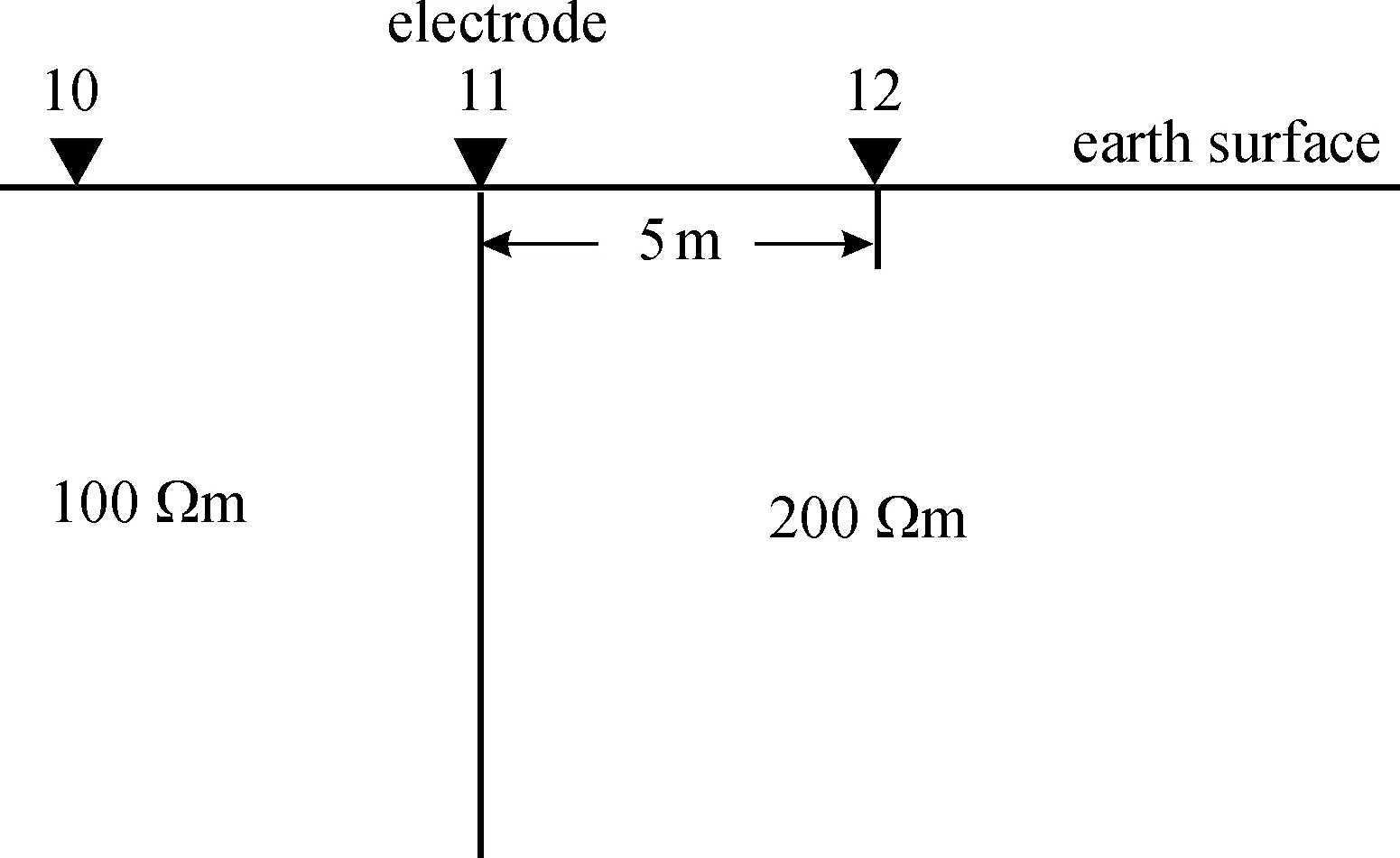
圖5 2D垂直不連續(xù)分界面模型(模型2)Fig.5 2D vertical uncontinue interface model (Model 2)

圖6 模型2有限元計(jì)算的對稱四極剖面與理論值對比(AO=7.5 m, MN=5 m)Fig.6 Apparent resistivity curves of schlumberger array of theory and FEM of Model 2

從圖6中可見，有限元計(jì)算的對稱四極剖面視電阻率與理論曲線擬合較好,只在分界面附近(50 m處)有兩個(gè)點(diǎn)誤差較大(最大相對誤差為1.996%)。分析誤差大的原因是，在分界面附近線性變化的插值函數(shù)難以擬合電位的劇烈變化。圖7、圖8分別為模型2理論及本文有限單元法α裝置視電阻率斷面圖，它們都很好地反映垂直分界面的形態(tài),等值線圖的形態(tài)也非常接近。

5.3 均勻大地中三維異常體模型(模型3)

模型3為在均勻大地中有一個(gè)10 m×10 m的低阻立方體,電阻率為10 Ωm, 頂面埋深為20 m， 圍巖電阻率為200 Ωm， 在低阻體外有5 m厚的過渡區(qū), 電導(dǎo)率從0.1 S/m線性變化到0.005 S/m。 布置10條測線, 線距10 m, 每條測線21個(gè)電極, 電極距10 m。 圖9為模型3的側(cè)視圖, 圖10為測線布置圖。 有限單元法網(wǎng)格節(jié)點(diǎn)為97 468個(gè), 電極間插入一個(gè)節(jié)點(diǎn)。 210個(gè)電極計(jì)算用時(shí)74.33 s, 平均每個(gè)電極解方程用時(shí)0.35 s, 迭代10次左右, 這也反映了對于均勻大地中異常體簡單模型的正演計(jì)算速度較快, 因?yàn)橄噜忞姌O的電位較為接近。

圖7 模型2理論α裝置視電阻率斷面圖Fig.7 Theory apparent resistivities section of α array of Model 2

圖8 模型2有限單元法α裝置視電阻率斷面圖Fig.8 FEM apparent resistivity section of α array of Model 2

圖9 模型3側(cè)視圖Fig.9 Side view of Model 3

圖10 模型3俯視及測線示意圖Fig.10 Vertical view of Model 3 and survey lines

有限單元法計(jì)算的各條測線視電阻率斷面圖如圖11所示,不同極距AO的視電阻率平面等值線圖如圖12所示，本文有限單元法所計(jì)算的視電阻率斷面圖和平面等值線圖能較好地反映三維低阻體的位置及形態(tài)特征。

6 結(jié) 論

(1)通過一維、二維及三維模型的正演計(jì)算，驗(yàn)證了本文齊次邊界條件下，電導(dǎo)率線性變化直流電測深三維有限單元法正演模擬方法的準(zhǔn)確性及有效性。

(2)采用改進(jìn)SSOR PCG迭代算法解線性方程組與直接解法相比，能極大提高計(jì)算速度。

(3)用OpenMP 進(jìn)行并行計(jì)算,并且采用相鄰電極供電所計(jì)算出來的電位作為當(dāng)前電極供電時(shí)的初始解,能極大減小求解的迭代次數(shù),提高計(jì)算速度。

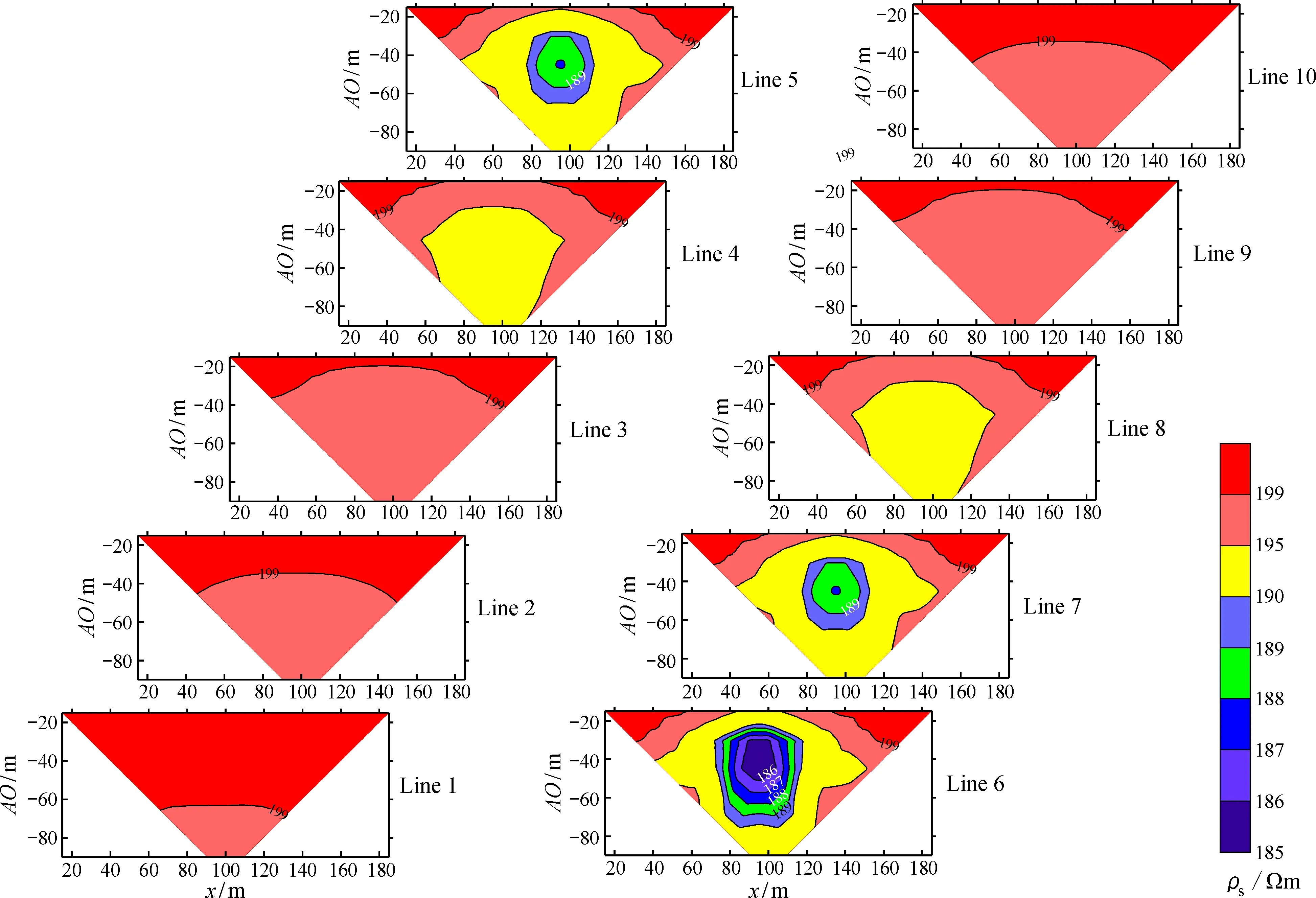
圖11 模型3有限單元法α裝置視電阻率斷面圖Fig.11 FEM apparent resistivity sections of Model 3

圖12 模型3有限單元法α裝置視電阻率平面等值線圖Fig.12 FEM apparent resistivity plane equivalence maps of Model 3