基于AdaGrad的GNSS-R鏡面反射點自適應預測算法

盛志超，周 勃，杜璞玉，秦 瑾，王 路

(1.上海航天電子技術研究所，上海 201109；2.東南大學，江蘇 南京 211189)

0 引言

GNSS-R技術是一種新型遙感技術，能夠實現對海面高度、海面風速和土壤濕度等多種環境要素的探測[1-2]。相比于傳統微波遙感載荷，GNSS-R載荷具有寬刈幅、高時空分辨率、低功耗和低成本等優點[3-5]。

GNSS-R遙感的探測區域是以鏡面反射點為中心的閃耀區——反射信號功率最集中的位置[6-7]。對鏡面反射點幾何位置的精確預測有2個作用：① 建立對GNSS-R遙感探測的坐標基準；② 實現對反射信號的實時開環跟蹤。鏡面反射點預測的精確與否，對GNSS-R遙感探測的建模與反演有直接影響。因此，如何快速有效地計算出鏡面反射點的位置，是GNSS-R技術的首要問題。

現有的鏡面反射點預測算法主要有Gleason算法[8]、S.C.Wu算法[9]和線段二分法[10]。Gleason算法的精度高但收斂速度慢；S.C.Wu算法的收斂速度快且穩定，但因其采用地球圓模型進行建模，需要加入復雜的校正；線段二分法是S.C.Wu算法的改進，其收斂速度快并且精度高，但存在不可避免的徑向和法向不統一問題。

鏡面反射點的預測過程本質上和深度學習中的“學習”過程是一致的，因此，一些統計學習理論可以用于鏡面反射點預測的優化。本文提出了一種基于AdaGrad優化的GNSS-R鏡面反射點自適應預測算法，能夠對學習效率進行自動調整，從而實現對鏡面反射點更高效、更精確的搜索。

1 鏡面反射點

GNSS-R幾何位置關系示意圖如1所示。圖1(a)中GNSS衛星發射GNSS信號，該信號到達地球表面時，在鏡面反射點所在的閃耀區發生散射和反射，反射信號由GNSS-R接收機接收[11-12]。在理想情況下，鏡面反射點滿足以下條件：① 鏡面反射點在地球表面；② 發射機—鏡面反射點—接收機是所有反射路徑中的最短路徑；③ 滿足斯涅耳定律——入射角等于反射角[13]。

圖1(b)中，R表示接收機，T表示發射機，S表示地球表面上的某點，O表示地心，M表示OC所在直線與RT所在直線的交點，U表示R關于OM的對稱點，C表示M關于RU的對稱點，αt，αr分別表示信號的入射角和反射角。

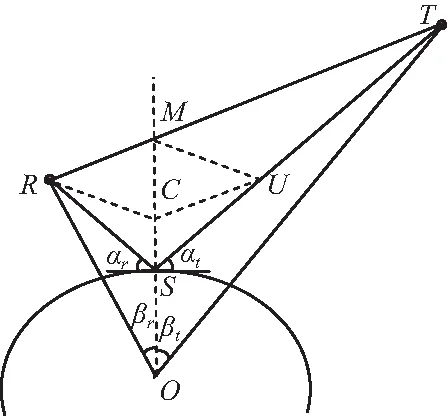
(b)二維視圖

在理想條件下，利用鏡面反射點滿足的3個條件，對鏡面反射點的預測問題等價于非線性約束條件下的非線性優化問題，其數學模型可以表示為：

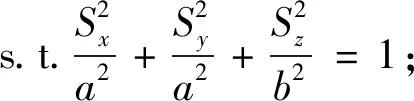
(1)

式中，f(S)的最小化函數是鏡面反射點預測的目標函數；R表示接收機；T表示發射機；S表示地球表面上的某點；Sx，Sy，Sz分別為S在地心坐標系下對應的三軸坐標；αt，αr分別表示信號的入射角和反射角。

2 鏡面反射點的估算

傳統鏡面反射點預測算法都是以入射角等于反射角為終止條件進行搜索的，得到的反射路徑長度不一定最短，不符合鏡面反射點的定義。本文提出的算法將直接從式(1)中的目標函數出發，在地球表面尋找使反射路徑長度最短的點，即鏡面反射點。下面會證明本文提出的算法所預測得到的鏡面反射點同時也滿足入射角等于反射角這一條件。

針對帶非線性約束條件的非線性優化問題，鏡面反射點初始值的設置會對算法的收斂速度以及結果的準確度產生重要影響。因此，本文提出的算法將通過以下2個步驟實現對鏡面反射點的預測：

① 利用發射機、地球、接收機的幾何關系，實現鏡面反射點的粗略估計；

② 利用AdaGrad優化算法求解最短路徑，實現鏡面反射點的精確估計。

2.1 鏡面反射點粗估

圖1(b)中存在如下數學關系：

|RM|=|MU|=|UC|
|RM|/|RT|=|RM|/(|RM|+|MT|)=
|CU|/(|CU|+|MT|)=
|SR|/(|SR|+|ST|)≈
|OR|/(|OR|+|OT|)。

(2)

由此可以得到，M的粗略估計值為：

M=R+RM≈R+[|OR|/(|OR|+|OT|)]×RT。

(3)

而鏡面反射點S1為M的星下點，則鏡面反射點的粗略估計值為：

S1=(OM/|OM|)×Re，

(4)

式中，Re為WGS-84坐標下M點對應星下點的半徑。

2.2 鏡面反射點精估

2.2.1 AdaGrad優化算法

深度學習使用數據對其構筑中的參數進行更新以達成訓練目的，該過程被稱為“學習”，“學習”的常見方法有梯度下降法及其變體，一些統計學習上的理論被應用在學習過程的優化上[14]。

針對反射路徑長度f(S)=|S-T|+|R-S|的最小化問題求解，同樣也可以通過梯度下降的方法實現對解的優化更新，其更新表達式為Sn+1=Sn-K·f(Sn)[15]。其中，K表示學習率，f(Sn)表示f(S)的梯度，即每一次迭代過程中的更新增量，其可以表示為：

(5)

梯度下降法在每一次迭代過程中，對解的更新都采用固定的學習率。學習率決定了參數移動到最優值的速度快慢。如果學習率太小，優化效率可能過低，算法收斂速度太慢；如果學習率太大，參數的收斂過程會產生震蕩，甚至無法收斂[16]。

本文采用深度學習中的AdaGrad優化算法。該算法是梯度下降法的一種變體，能夠在每一次迭代過程中對學習率進行調整，當離目標函數最優解較遠時，學習率較大，朝最優解移動得越多[17]。隨著迭代次數的增加，學習率逐漸減小。

基于AdaGrad計算鏡面反射點的算法具體如下：

① 對參數進行初始化：

設置全局學習率ε為1，鏡面反射點的初值為上節鏡面反射點的粗估值S1，常數δ為10-7，梯度累積變量τ為0。

f(Sn)n=N(Sn)×f(Sn)×N(Sn)，

(6)

式中，N(S)表示S的單位法向量。

監管點設立后珠海局多措并舉，嚴密監控監管點周邊水域的渡口，渡船以及橋梁的安全，發揚“敬業、工匠、團隊”的精神，每天安排執法人員前往“海躉1556”值守，重點開展電子巡航和對赤粉水道、荷麻溪水道、泥灣門水道、虎跳門水道、磨刀門水道進行巡航檢查：“海躉1556”監管點設立以來，共檢查船舶1716艘次，檢查渡口541次，橋梁水域巡查1141次，開展夜巡56次。隨著“海躉1556”監管點的投入使用，珠海局依托該監管點進一步提高了現場監管效率，加大了違章、違法行為的打擊力度，強化了轄區渡口、橋梁、岔河口等重點水域的監管力度，周邊水域通航秩序大有改觀，未發生重大事故，極大地助力了“平安西江”建設。

③ 計算累積梯度平方和τ：

τ=τ+f(Sn)2。

(7)

④ 計算更新增量ΔS：

(8)

⑤ 利用ΔS，對Sn進行更新：

S′=Sn+ΔS。

(9)

⑥ 將S′映射到地球表面，得到相應的鏡面反射點的下一個解Sn+1：

Sn+1=(OS′/|OS′|)×Re(S′)。

(10)

⑦ 計算更新幅度：

COR=|Sn+1-Sn|。

(11)

如果更新幅度COR大于設定的閾值則繼續進行下一次迭代，否則結束迭代，輸出鏡面反射點的最優解。

2.2.2 預處理

預處理實現將WGS橢球面通過坐標變換映射成單位圓[18]。其坐標變換的矩陣F為：

(12)

式中，a=6 378 137 m是赤道半徑長度；b=6 356 800 m為經線半徑長度。

坐標系映射的示意如圖2所示，其中，R表示接收機，T表示發射機，SWGS-84表示WGS-84橢球面上的鏡面發射點，q表示f(S)在點SWGS-84處的梯度，n表示點SWGS-84處的法向量，Spro表示單位圓上的鏡面反射點，q′表示f(S)在點Spro處的梯度，n′表示點Spro處的法向量。

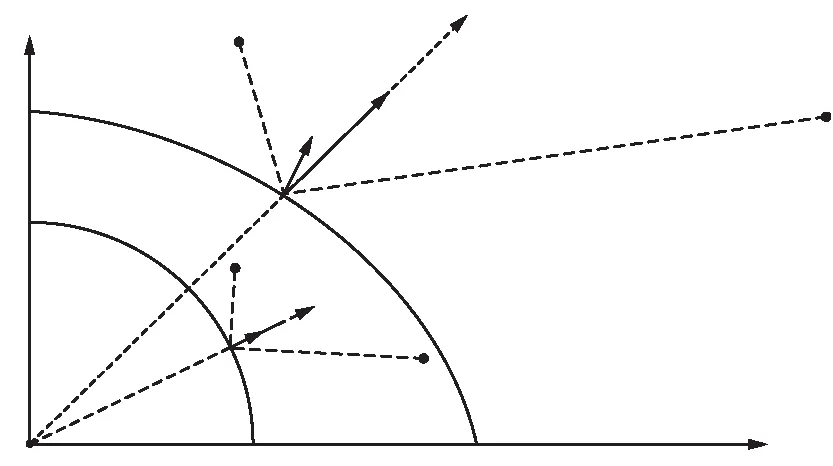
圖2 坐標映射示意

將WGS-84橢球面通過坐標變換映射成單位圓，具有以下2個作用：

① 實現了地球尺度和收斂因子數量級的統一。通過坐標變換，將赤道半徑a=6 378 137 m，經線半徑b=6 356 800 m的WGS84橢球面映射成單位圓，使地球尺度和收斂因子在同一數量級上，以便在鏡面反射點的最優解求解過程中能夠快速獲得有效解。

② 實現鏡面反射點的徑向和法向的統一。如圖2所示，點SWGS-84處的目標函數下降最快的方向為f(Sn)的方向，即圖中徑向q。因此，算法只有在徑向q的水平分量為0時收斂。但是徑向q的水平分量只有在R，O，T共線且該直線與地平線垂直的時候才為0，即入射角為90°時。而在單位圓中，徑向q與法向n共線，當算法收斂時，即修正幅度COR為0時，徑向q的水平方向分量為0，又因為q=(Sn-T)/|T-Sn|+(Sn-R)/|R-Sn|，可知徑向q是2條單位向量的矢量和，只有入射角等于反射角時，徑向q無水平分量。

2.2.3 算法流程

上面提出的基于AdaGrad計算鏡面反射點算法的基礎上，增加了預處理操作，因此本文總的算法流程如圖3所示。

圖3 算法流程

3 仿真分析

利用STK和Matlab進行聯合仿真實驗。GNSS衛星采用GPS衛星，軌高20 200 km，LEO衛星軌高700 km，進行了4種算法反射路徑長度和運算效率比較仿真以及本文算法迭代次數穩定性仿真。發射機T的坐標為(-11 178 791.991 29，-13 160 191.204 99,20 341 528.127 54)，接收機R的坐標為(-4 069 896.491 51,-3 583 236.963 73,4 527 639.271 75)。

3.1 4種算法反射路徑長度和運算效率比較仿真

4種算法反射路徑長度和運算效率仿真圖如圖4所示。

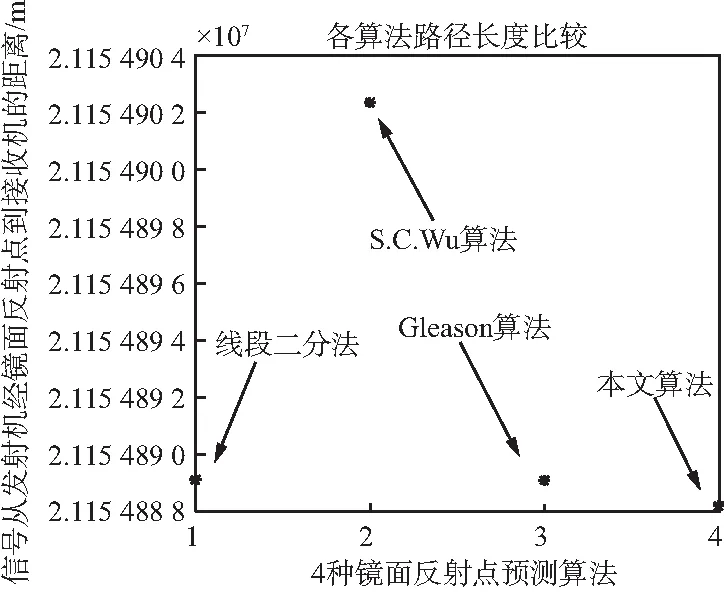
(a)反射路徑長度

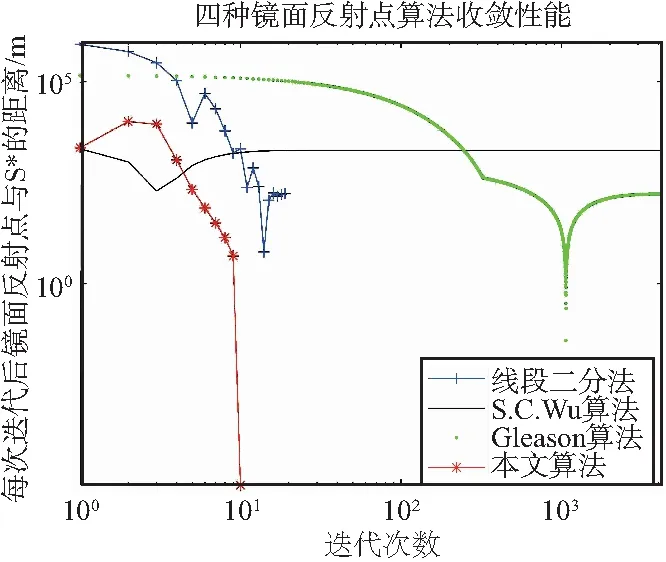
(b)收斂性能比較圖4 種算法反射路徑長度和運算效率仿真

從圖4可以看出，S.C.Wu算法得到的反射路徑最長，其獲得的鏡面反射點與真實鏡面反射點距離最遠，因此，該算法計算精度最差。其他3種算法的路徑長度接近，其中本文算法的路徑長度最短，滿足最短反射路徑的特點。4種算法預測得到的鏡面反射點在地圖上位置相近，說明本文算法得到的鏡面反射點是有效的。

將仿真中本文算法計算得到的鏡面反射點S*作為參考，對算法的收斂性能進行分析。圖4(a)為4種鏡面反射點算法收斂性能的比較結果圖。從圖4(b)可以看出，S.C.Wu算法無法收斂，Gleason算法迭代次數多，運算速度較慢。本文算法迭代次數最少，速度最快。

3.2 本文算法高效性統計意義仿真

利用STK生成的1顆軌高700 km的LEO衛星和31顆GPS衛星進行仿真，仿真時間是從2015年3月7日00:00:00開始的24 h。GNSS-R接收機的下視天線的波瓣寬度為±45°，采用的選星策略是GNSS-R接收機的仰角不低于75°。

分別利用本文算法和線段二分法計算32 750組符合條件的數據。本文算法和線段二分法效率統計圖如圖5所示。通過比較可以看出，本文算法每次的迭代次數穩定在14次以內，線段二分法每次的迭代次數集中在13～17次，部分數據的迭代次數超過25次，因此本文算法從統計意義上來說運算效率明顯優于線段二分法。

3.3 結論

Gleason算法收斂速度慢，但是位置較為精確；而S.C.Wu算法因其精度低、無法達到預設的精度要求，出現了無限次迭代，算法無法終止；線段二分法是S.C.Wu算法的改進，因此它繼承了S.C.Wu速度快的優點，并且利用WGS-84橢球面，其預測得到的鏡面反射點較為精確，但沒有解決徑向、法向不統一的問題。本文提出的算法能夠根據更新幅度自適應的改善學習率，因而能更快速地到達最優解。通過仿真結果可以看出，本文算法的結果相比于其他算法更為精確。此外，根據圖5結果可以得出，本文算法統計意義上也更加高效。

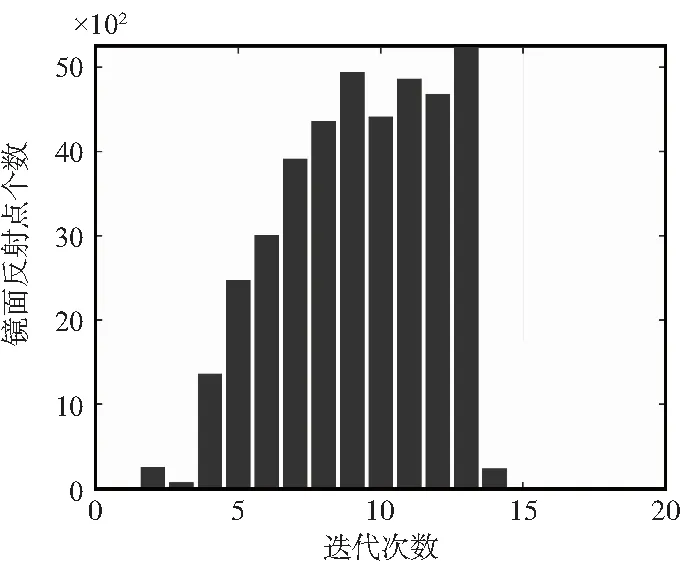
(a)本文算法效率統計圖

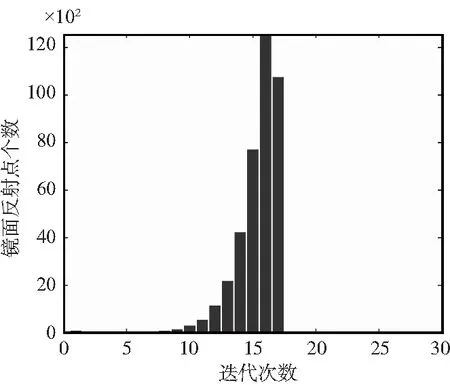
(b)線段二分法效率統計圖圖5 本文算法和線段二分法算法效率統計仿真

4 結束語

本文提出了基于AdaGrad的GNSS-R鏡面反射點預測算法，具有精度高、速度快的優點。該算法將深度學習優化算法應用于鏡面反射點的預測過程，通過自適應地調整學習率，提高算法收斂速度，滿足星載環境中的實時性需求。該算法在預處理過程中實現鏡面反射點徑向和法向的統一，進一步提高了算法的預測速度。仿真結果表明，該算法收斂速度快，預測精度高。相比于傳統鏡面反射點預測算法，該算法在預測速度方面具有明顯優勢，對于GNSS-R載荷搭載具有一定的參考意義。