殘差修正GM(1,1)模型在房屋建筑施工面積預測中的應用
陳佳琪 宋冀龍

摘? 要:房屋建筑施工面積可以有效反映建筑業的現實狀況,對房屋建筑施工面積的預測結果可以為政府、企業在未來的策略方案提供更加有效的參考。采用傳統GM(1,1)模型和改進后的殘差修正GM(1,1)模型分別對房屋建筑面積統計數據進行預測,通過兩種模型預測的結果,可以得出改進后的殘差修正GM(1,1)模型可以在一定程度上減少誤差,可以更有效地對房屋建筑面積進行預測。
關鍵詞:灰色系統;殘差;GM(1,1)模型;房屋建筑施工面積
中圖分類號:TU765? ? ? ? 文獻標志碼:A 文章編號:2095-2945(2019)27-0173-03
Abstract: The construction area of the building can effectively reflect the actual situation of the construction industry, and the prediction results of the construction area of the building can provide a more effective reference for the government and enterprises in the future. The traditional GM(1,1) model and the improved residual correction GM(1,1) model are used to predict the statistical data of building area, and the results are predicted by the two models. It can be concluded that the improved residual correction GM(1,1) model can reduce the error to a certain extent, and can predict the building area more effectively.
Keywords: gray system; residual; GM (1,1) model; building construction area
前言
建筑業是國民經濟的重要物質生產部門,與我國經濟社會、人民生活水平的提高有著密切的關系[1]。建筑業是一個非常龐大且復雜的系統,它的發展狀況是由許多因素共同作用的結果。由于因素之間的關系不明確,且難以定量加以描述,可以知道建筑業屬于典型的灰色系統。
灰色系統理論在鄧聚龍教授提出后得到了快速的發展,從最初的在經濟管理系統、控制系統、農業系統等領域的應用,到在現在的社會生活等各個領域的應用,成果豐富且應用性較高。到現在為止灰色系統理論已經形成了以系統分析、信息處理、建模、預測、決策、控制為主要內容的理論體系[2]。
本文先對建筑業房屋建筑施工面積數據進行數據序列檢驗,然后在GM(1,1)模型[2]的基礎上,建立殘差修正模型[3-6],對其進行預測,驗證該模型的有效性。結果表明了改進的修正模型對現有數據的預測具有更高的預測精度,效果更好。
1 預測模型的建立
1.1 數據序列的檢驗
若發現精度檢驗預測效果一般或不好,需要對原模型進行修正。
1.4 殘差修正
2 預測模型的應用
本文采取的數據是從國家統計局公布的建筑業房屋建筑施工面積中摘取了2012-2017年的數據(986427.45,1132002.90,1249826.35,1239717.60,1264216.27,1318374.06)。
2.1 數據序列檢驗
光滑性檢驗:原始數據為x(0)(k)=(986427.45,1132002.
90,1249826.35,1239717.60,1264216.27,1318374.06)。累加一次得x(1)(k)=(986427.45,2118430.35,3368256.7,460797
4.3,5872190.57,7190564.63)。由(1)式得:當k>3時,準光滑條件滿足。
準指數檢驗:由x(0)(k)=(986427.45,1132002.90,12498
26.35,1239717.60,1264216.27,1318374.06)和(2)式可以得到當k>1即可滿足準指數檢驗條件。
由上述可知,當k>3時,符合數據序列檢驗要求,故可以建立GM(1,1)模型。
2.2 進行GM(1,1)模型預測和殘差修正
以2012-2017年的數據(986427.45,1132002.90,1249
依據殘差公式(7)式,得到GM(1,1)模型預測后的殘差序列為?著(0)=(0,-33121.5128,48063.9264,165.0622,-143
14.714,-361.0699)。
取k0=2,得新數據列(-33121.5128,48063.9264,165.06
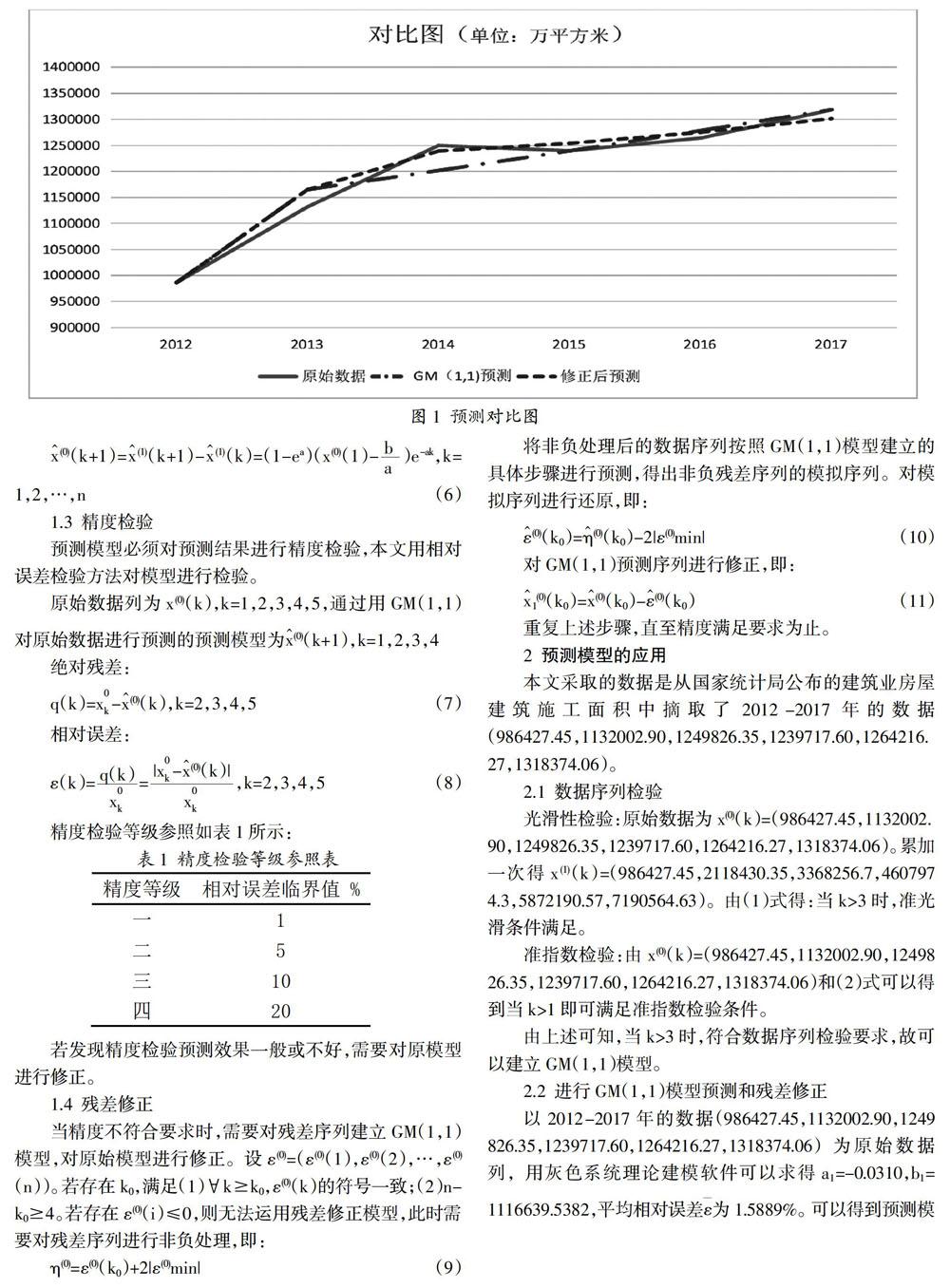
原始數據、傳統GM(1,1)模型預測數據和修正模型預測數據對比如圖1所示。
3 結論
建筑業系統是灰色系統,GM(1,1)模型對房屋建筑施工面積進行預測有較好的預測精度。通過對模型進行殘差修正可以發現,改進后的模型提高了預測的精度,平均相對誤差由1.589%減少到1.415%。結果建立在數學模型基礎之上且精度很高,有很高的可信度,可以為有關部門和人員提供參考。
參考文獻:
[1]朱娟,易冰源.建筑業在我國國民經濟中產業地位的量化分析[J].工程經濟,2019,29(02):39-43.
[2]劉思峰,謝乃明.灰色系統理論及其應用(第四版)[M].科學出版社,2010.
[3]姚裕盛,徐開俊,楊泳.基于GM(1,1)殘差修正模型的飛行訓練量預測[J].西安航空學院學報,2018,36(01):78-82.
[4]楊瑞波,陳建宏,鄭海力,等.殘差修正GM(1,1)模型在煤礦事故預測中的應用[J].礦業研究與開發,2011,31(01):73-76.
[5]張新生,趙夢旭,王小完.尾段殘差修正GM(1,1)模型在管道腐蝕預測中的應用[J].中國安全科學學報,2017,27(01):65-70.
[6]趙卓峰,楊宗潤.基于殘差修正GM(1,1)模型的車流量預測[J].計算機科學,2017,44(04):96-99+130.

