基于改進蟻群算法的鐵路乘務交路計劃的編制

王東先 孟學雷 喬俊 湯霖 焦志臻

摘 要：針對提高鐵路乘務交路計劃編制質量和效率的問題，將乘務交路計劃編制問題抽象為單基地、均衡行駛路程的多旅行商問題（MTSP），引入均衡因子，建立了以乘務交路用時少和子乘務交路間任務均衡為目標的數學模型。針對該模型提出了一種雙重策略蟻群優化算法，該算法首先構建滿足時空約束的解空間，分別對乘務區段節點和接續路徑設置信息素濃度，然后采用雙重策略狀態的轉移概率，使螞蟻遍歷所有乘務區段，最終找到符合乘務約束規則的子乘務交路。最后運用廣深線城際鐵路數據對設計的模型及算法進行檢驗，經與遺傳算法的實驗結果對比分析表明：在相同的模型條件下，運用雙重策略蟻群優化算法編制的乘務交路計劃乘務交路個數減少了約21.74%、乘務交路總時長降低了約5.76%、交路超勞率為0。運用所設計的模型和算法編制乘務交路計劃能夠減少乘務計劃交路時長，均衡工作量，避免產生超勞交路。

關鍵詞：鐵路;乘務交路計劃;均衡因子;多旅行商問題;雙重策略蟻群算法

中圖分類號：TP301.6

文獻標志碼：A

Railway crew routing plan based on improved ant colony algorithm

WANG Dongxian1， MENG Xuelei1*， QIAO Jun1， TANG Lin1， JIAO Zhizhen2

1.School of Traffic and Transportation， Lanzhou Jiaotong Unirersity， Lanzhou Gansu 730070， China;

2.China Railway Lanzhou Group Company Limited， Wuwei South Station， Wuwei Gansu 733000， China

Abstract：

In order to improve the quality and efficiency of railway crew routing plan， the problem of crew routing plan was abstracted as a Multi-Traveling Salesman Problem （MTSP） with single base and balanced travel distance， and a equilibrium factor was introduced to establish a mathematical model aiming at less crew routing time and balanced tasks between sub-crew routings. A dual-strategy ant colony optimization algorithm was proposed for this model. Firstly， a solution space satisfying the space-time constraints was constructed and pheromone concentration was set for the node of the crew section and the continuation path respectively， then the transitional probability of the dual-strategy state was adopted to make the ant traverse all of the crew segments， and finally the sub-crew routings that meet the crew constraint rules were found. The designed model and algorithm were tested by the data of the intercity railway from Guangzhou to Shenzhen. The comparison with the experimental results of genetic algorithm shows that under the same model conditions， the number of crew routing in the crew routing plan generated by double-strategy ant colony optimization algorithm is reduced by about 21.74%， the total length of crew routing is decreased by about 5.76%， and the routing overload rate is 0. Using the designed model and algorithm to generate the crew routing plan can reduce the crew routing time of crew plan， balance the workload and avoid overload routing.

Key words：

railway; crew routing plan; equilibrium factor; Multi-Traveling Salesman Problem （MTSP）; dual-strategy Ant Colony Algorithm （ACA）

0 引言

鐵路乘務計劃是依據列車運行圖、機車交路（動車組交路）、相關乘務規則、車站設備條件等限制因素編制的，對乘務人員（司乘）出、退乘時間和地點及擔當車次等做出的詳細安排，保證了列車運行計劃的順利實施。其中，列車運行圖包含了待完成的乘務任務，機車交路（動車組交路）規定了機車（動車組）擔當運輸任務的固定周轉區段，乘務規則限定了乘務人員的工作時間，車站設備條件限制了車站是否是乘務基地及具備司乘人員換乘或休息的條件。

因為在編制乘務計劃過程中需要同時考慮到乘務交路計劃和乘務排班計劃相關的大量約束，導致乘務計劃的編制有難度大、效率低的特點。所以，為了合理優化乘務計劃編制，有效提高編制效率，乘務計劃往往被分為乘務交路計劃和乘務排班計劃。乘務交路計劃是乘務排班計劃的基礎，乘務排班計劃編制的優劣取決于乘務交路計劃。本文針對乘務交路計劃編制，做出進一步的討論。針對乘務交路計劃編制問題，文獻[1]建立了0-1整數規劃和動態規劃模型，利用拉格朗日方法求得問題的下界，設計了樹搜索算法求得最優解。文獻[2]利用改進的遺傳算法結合Dijkstra法分階段編制了香港輕軌乘務計劃，但是該模型對于求解“點多線長”的鐵路乘務計劃有一定局限性。文獻[3]采用列生成技術求解了動車組乘務交路計劃。文獻[4]運用了禁忌搜索和圖著色理論編制了乘務計劃。文獻[5]重點研究了工作效率對于乘務計劃編制的影響，并用蟻群算法進行了求解，但是沒有考慮乘務交路的均衡性。文獻[6]利用SE（Simulated Evolution）方法編制了京滬高鐵的乘務計劃。文獻[7]借鑒文獻[6]的SE方法求解了乘務排班計劃，但是沒有考慮乘務交路計劃。文獻[8]首次在國內將列生成技術應用到了乘務交路計劃的編制，并把乘務排班計劃問題抽象成了旅行商問題，但是該算法在求解初始可行解時效率較低。文獻[9]結合了列生成技術和分支定界法，進而提出了求解乘務交路計劃的分支定價算法。文獻[10]將客運專線的乘務交路計劃轉化為特殊的旅行商問題，并提出了K條徑路的最大最小螞蟻系統（K-Max-Min Ant System， K-MMAS）算法，但是該模型沒有考慮到乘務人員的任務均衡性。文獻[11]將乘務計劃編制問題拆分為最優回路構造、回路循環優化和排班三個子問題，并設計了遺傳算法進行求解，但是編制步驟過多，不利于鐵路乘務交路計劃的快速編制。文獻[12]將乘務交路計劃的編制問題分解為值乘區段集合的覆蓋和乘務交路段的匹配兩個子問題，并設計了改進的蟻群算法進行求解，但是該模型沒有考慮乘務計劃與乘務交路計劃的協同優化。文獻[13]根據現場調研統計的結果，建立了基于乘務人員偏好性的乘務交路計劃，但是對于復雜的交路，沒有給出具體的評價值標定方法。文獻[14]通過采用最近鄰域搜索算法和模擬退火算法求解了乘務交路計劃的數學規劃模型，但是該模型沒有考慮到乘務交路的均衡性，不適用于城際鐵路乘務計劃的編制。文獻[15]建立了基于遺傳算法的乘務計劃編制的求解方法，同時對系統的人機交互調整功能進行了設計。文獻[16]提出了基于時空接續網絡和網絡流模型的求解策略來編制高速鐵路乘務計劃，并利用了拉格朗日松弛算法進行求解，但是該算法的迭代步長由經驗公式自行設定，缺乏論證。回顧前人研究成果可以看出，國內大多數學者的研究重點集中于高速鐵路宏觀層面的乘務計劃，但是，對于乘務交路計劃研究較少。本文在總結已有的研究成果基礎上，結合鐵路乘務規則及其特點，將乘務交路問題抽象為多旅行商問題（Multi-Traveling Salesman Problem， MTSP），最后針對本文研究問題設計基于雙重策略的蟻群算法求解該模型。

1 乘務交路計劃數學模型的建立

鐵路乘務交路計劃編制是機車乘務計劃的核心問題。乘務交路計劃編制過程中需綜合考慮鐵路乘務調度規則及資源約束條件，在列車運行圖的基礎上，將所有值乘區段組合成若干個可行乘務交路，以勞動強度均衡為原則分配乘務任務，建立乘務時長最短，乘務人員“用戶體驗”最佳的乘務調度計劃。

1.1 問題描述

最優乘務交路計劃的一項重要指標是使用最少的乘務人員（組）完成上級下達的運行圖任務。編制鐵路機車乘務交路計劃的主要步驟如下。

1）收集列車運行信息。根據列車運行圖和機車交路（動車組交路），獲取列車車次、發站、到站及動車組在乘務基地所在站和換乘站的停留作業時間。

2）選定換乘車站。乘務人員換乘車站的選取與車站的設備條件密切相關，選取的車站必須是具備換乘條件的。根據運行圖數據，以單條運行線為研究對象，把運行線上的所有車站分為3類：具備換乘條件的乘務基地所在車站、具備換乘條件的非乘務基地所在車站、不具備換乘條件的非乘務基地所在車站。

3）劃分乘務區段。根據列車運行信息，在輪乘制的值乘模式下，按照乘務人員一次連續工作時長標準，以可換乘車站為節點，把運行線逐條劃分為若干滿足乘務規則的乘務區段。

4）建立可行的乘務大區段。一個乘務大區段由兩個或兩個以上的乘務區段嚴格按照乘務規則（時空接續規則）組合而成。乘務人員（組）完成一個乘務大區段值乘任務的過程是指乘務人員從乘務基地開始值乘，到達換乘公寓所在站，休息一定時間后值乘另一任務最終返回乘務基地的過程。

5）把若干可行乘務大區段按照乘務接續規則組合成覆蓋整個區段的乘務交路。

1.2 乘務交路計劃時空規則

1）時間接續乘務規則。相鄰的兩乘務區段必須要滿足時間接續性，即前一個乘務區段的到站時刻必須嚴格早于后一個乘務區段的發車時刻。如果某一個乘務區段結束后乘務人員正好要換乘（或駐班休息），那么乘務人員在該站的換乘時間必須嚴格大于這兩個相鄰乘務區段的接續時間。

2）空間接續乘務規則。相鄰的兩乘務區段必須要滿足空間接續性，即前一個乘務區段的到站必須是后一個乘務區段的發站，保證乘務交路集合必須覆蓋所有的乘務區段。因為鐵路運行線相比其他交通運行線路較長，經常是跨城市甚至是跨省份的，所以乘務交路必須考慮乘務人員的歸屬地因素，保證最終生成的乘務交路的發站和到站是同一車站。

1.3 乘務交路數學模型

若把乘務區段當作MTSP中的城市，兩相鄰乘務區段之間的接續就可以看作是城市與城市之間的距離，由于每個子乘務交路都需一個乘務組值乘，故子乘務交路的個數就是所需乘務人員（組）的個數，即旅行商數目。設有N個子乘務交路，則N個子乘務交路從列車運行圖過表時刻（默認列車運行圖過表時刻為18：00）開始，各子乘務交路有且僅有一個乘務組訪問，最后回到過表時刻，形成封閉回路。結合列車運營特點，乘務交路計劃編制問題可以抽象為單基地、均衡行駛路程的MTSP。

將所有乘務區段抽象為點集V，所有的乘務區段之間的接續關系抽為成邊A，簡化后的乘務交路區段可視為有向圖G，即建立具有U個節點的乘務交路區段有向圖G=（V，A）。其中Vi（Vi∈J）是節點集合V中的節點，本文將節點類型分為3類：乘務區段點集合、乘務基地所在站（起點）集合、乘務基地所在站（終點）集合。其中乘務區段點集合含有以下六點屬性：tfi、tdi、sfi、sdi、tti、r 。

弧aij（A={aij/aij=（vi，vj）;vi，vj∈V}）（i、 j=1，2，…，U）表示集合A中的一條連接弧，根據相關乘務規則，本文將弧集合A分為4種類型：接續弧集合、外段（折返段）駐班弧集合、出乘弧集合、退乘弧集合。四種不同類型的弧集合都含有以下兩點屬性：ttij、σij。模型中的符號定義如表1所示。

定義1 S={si/si=0，si=1，si=2}（i=1，2，…，U）為列車運行圖中的車站集合，令Wsi為第i個車站的屬性，則Wsi=0表示不具備換乘條件的非乘務基地所在車站，Wsi=1表示具備換乘條件的非乘務基地所在車站，Wsi=2表示具備換乘條件的乘務基地所在站。

定義2 H={Hk/k=1，2，…，N}，令Hk為所有子乘務交路的集合，通常tfi不大于可調度的乘務組總數。

考慮子乘務交路間工作量均衡的乘務交路計劃編制問題目標函數包含兩部分：1）乘務交路總時長最少;2）使子乘務交路之間的乘務時間相差最小。通過引入均衡因子將兩部分目標統一為：

Z=min{∑Nk=1Zk+δ/ε}; ε∈Z*（1）

Zk=∑Ui=1∑Uj=1[ttij+（tti+ttj）/2]xijk（2）

δ=∑Nk=1∑Ui=1∑Uj=1tdkj-（tdkj-tokj）·xijk+tti+ttjN-12N-1（3）

s.t. Sdi=Sfj; i， j=1，2，…，U（4）

∑h∈Hk ∑i， j∈Aij，φi=φlxijk≥1; l∈L， i，? j=1，2，…，U（5）

∑（i， j）∈Aijxijk=∑（j，i）∈Ajixjik; i∈Vli，i∈Vlj，i， j=1，2，…，U（6）

WSfhk=WSdhk≠0且Sfhk=Sdhk; k=1，2，…，U（7）

∑h∈Hk，（i， j）∈Aoijxijk=1; i∈Vli，j∈Vlj，i， j=1，2，…，U（8）

∑h∈Hk，（i， j）∈Adijxijk=1; i∈Vli，j∈Vlj，i， j=1，2，…，U（9）

tdkj≤tdki+（1-xijk）M+tto+ttj ;

（i， j）∈Aoij， i∈Voi， j∈Vli，l∈L， i， j=1，2，…，U（10）

tdkj≤tdki+（1-xijk）M+ttij+ttj;

（i， j）∈Acij，i， j∈Vli，l∈L，i， j=1，2，…，U（11）

tdkj≤tdki+（1-xijk）M+ttd;

（i， j）∈Adij， i∈Vli， j∈Vdi， l∈L， i， j=1，2，…，U（12）

tdkj≤tdo+（1-xijk）M+ttj;

（i， j）∈Asij， l∈L， i， j=1，2，…，U（13）

tdki≥Tcmin-（1-xijk）M-ttd;

（i， j）∈Asij∪Adij， l∈L， i， j=1，2，…，U（14）

tdki≤Tcmax， i∈Vli， l∈L， i=1，2，…，U（15）

tokj≤toki+（1-xijk）M+ttj（16）

∪Nk=1Hk=H（17）

式（1）中：Zk為乘務交路時長，具體表達式為式（2）;δ為子乘務交路間乘務任務分配均衡性，具體表達式為式（3）。目標函數式（1）旨在尋求可以使得乘務交路計劃總時長最小的同時盡量達到每條子乘務交路任務均衡的效果。其中ε為均衡因子，ε取較大的值時，表明總目標受交路總時長的影響較大，此時每條乘務交路時長差異較大，均衡交路任務的效果不理想。在正常情況下，可以根據乘務基地在不同情境下的歷史乘務數據，得到相應數值。在應急條件下，ε可根據實際需求設定為無窮大值，這種情況下乘務交路間的均衡性不再成為重要約束因素，以此來保證救援乘務組能夠快速機動地到達事故地點。均衡因子與目標函數的關系圖如圖4所示。式（4）為互異乘務區段接續空間約束，即為緊前乘務區段的到站與緊后乘務區段的發站必須是同一車站;式（5）表示所有劃分的乘務區段至少被覆蓋一次，若某些乘務區段超過一次，則認為該乘務區段為乘務人員“便乘”;式（6）為節點處流平衡約束：表示對于每個乘務區段節點而言，僅有一條邊進，一條邊出;式（7）描述交路閉合性約束，即乘務大區段的發站（到站）與到站（發站）必須是同一車站，且車站必須是乘務基地所在站（或乘務公寓所在站）;式（8）表示所有乘務大區段的起始弧必須是出乘弧;式（9）表示所有乘務大區段的終止弧必須是退乘弧;式（10）表示乘務大區段中的機車乘務人員出乘時長需滿足乘務規則約束;式（11）表示乘務大區段中乘務區段之間接續時長需滿足乘務規則約束;式（12）表示乘務大區段中的乘務人員退乘時長參數需滿足乘務規則;式（13）描述了乘務人員在乘務公寓駐班或調休后，乘務大區段累計時長需滿足乘務規則約束;式（14）、式（15）分別為乘務人員退乘或在乘務公寓駐班時，乘務大區段累計時長需滿足乘務規則;式（16）為乘務人員連續值乘累計時長需滿足的乘務規則;式（17）表示子乘務交路的集合需組成一個完整的乘務交路計劃。

2 雙重策略蟻群算法

顯然MTSP為NP-Hard問題，常用的解決方法包括分支定界法、線性規劃法、動態規劃法等。但是，隨著問題規模的增大，造成了組合爆炸的情況，精確算法難以求解，啟發式算法會體現出它特有的優勢。對于基本蟻群算法，一次循環某一路徑走過的螞蟻越多，累積的信息素就越多，而未被走過路徑的信息素將減少，根據與信息素有關的轉移概率計算出下一步任意可供選擇轉移位置的轉移概率后，采用比例方式（輪盤賭）方式確定。由于信息素的差別過大，且具有揮發性，可能導致某些路徑被選擇的比例過大，陷入局部最優解。同時初始路徑上信息素的水平一致，算法初期人工螞蟻的運動軌跡具有較強的隨機性，雖然通過啟發性信息能夠向較優路徑進化，但當求解問題規模較大時，不容易在短時間內從大量路徑中找出較優路徑，為了提高搜索效率，增加螞蟻搜索路徑的多樣性，本文提出了雙重信息素、雙重策略的改進蟻群算法，對基于MTSP的乘務交路問題進行求解。算法構建步驟如下。

1）生成解構建圖。

將經切割運行線后得到的乘務區段，按相應的乘務規則組合成若干乘務大區段，令所有乘務大區段遍歷所有乘務區段。根據抽象的乘務交路MTSP，解構建圖由所有表示乘務區段的節點和若干虛擬“原點”組成，其中“原點”是乘務大區段的起點和終點，若干“原點”實質上是一個點經過不斷復制得到的具有相同特性的離散點。

2）構建解空間。

讓所有螞蟻從某“原點”出發，每個螞蟻按照某一概率選擇乘務大區段的初始節點，設定初始節點的始發車站為φc，φc=0表示始發車站是乘務基地所在車站;否則φc=1。螞蟻按照某一概率選擇待接續的節點，如果累計時長尚未達到乘務大區段的乘務時長標準，則繼續選擇待接續的節點，直到接續一系列的節點后返回該“原點”形成一個回路，即乘務大區段。設定乘務大區段的到站為φd，φd=0表示到站是乘務基地所在車站，否則φd=1。若乘務大區段滿足φc·φd=0 ，則表示得到了一個滿足時空約束的乘務大區段，否則螞蟻繼續搜索，直至使得乘務大區段滿足φc·φd=0。螞蟻重復該過程構建解空間，當所有節點都被乘務大區段遍歷時，算法完成了解構建。

3）初始化及更新雙重信息素。

由于在解構建圖中節點和路徑具有同等的重要性，故本文對節點和路徑都定義了信息素濃度。設定全部路徑上的信息素濃度為τij，全部節點上的信息素濃度為τi。τij表示螞蟻處在節點i時，接續節點j的重要程度。τi表示螞蟻處在“原點”時，選擇節點i作為下一個乘務大區段起始節點的重要程度。其中，路徑和節點的信息素初始濃度設定如下：

τij（0）=1A2-A， i≠j

0，其他（18）

τi（0）=1/A（19）

式（18）、式（19）中A表示互異乘務區段節點之間的接續頻數。

信息素濃度與各乘務節點和路徑是否參與了最優解的構建成正相關。在最優螞蟻每次迭代后，各路徑和節點上信息素的更新取值設定如下：

τij（n+1）=ρτij（n）+Δτij（20）

τi（n+1）=ρτi（n）+Δτi（21）

Δτij=1/Zibest， eij∈sibest

0，其他 （22）

Δτi=1/Zibest， starti=1

0，其他（23）

式（20）、式（21）中ρ為信息素揮發因子（0<ρ<1），n代表迭代次數;式（22）、式（23）中Δτij、Δτi 分別為每次迭代過程中的信息素增量。starti為0-1變量，當乘務區段的節點i在最優解中出現作為某個乘務大區段的起點時1，否則取0。

螞蟻從“原點”出發，以τi的期望搜索到乘務區段節點i （即乘務大區段的起始節點），此時螞蟻以τij的期望繼續搜索到下一個乘務區段節點j，以此類推，根據某一概率選擇下一個乘務區段的節點，若其累計時長尚未達到乘務大區段的乘務時長標準，則繼續選擇下一個節點，直到接續一系列的乘務區段后返回該“原點”，形成一個回路，即乘務大區段。根據初始信息素濃度的設定（式（18）、式（19）），顯然τi（0）>τij（0）。通過設置雙重信息素全局更新策略，在每次迭代結束后，只允許全局最優解釋放信息素。在最優路徑上，螞蟻才釋放信息素，同時信息素才會揮發，這點非常重要，因為在信息素更新時的時間復雜度從O（n2）降到了O（n），所以螞蟻可以在短時間內從大量路徑中找出較優路徑，提高螞蟻的搜索效率。

4）基于雙重策略狀態的轉移概率。

①當第k只螞蟻所在的乘務區段節點i不是原點時，由節點i向下一個乘務區段節點j轉移的概率為：

Pkij=[τij]α·[ηij]β∑l∈Vli[τil]α·[ηil]β， j∈Vli

0，其他（24）

其中：ηij為預見度，表示從乘務區段節點i轉移到乘務區段節點j的預見程度。Vli表示螞蟻待訪問的節點集合，隨著迭代次數的增加，Vli中的元素不斷減少，直至為空，即表示所有乘務區段節點全部遍歷完畢。α表示殘留信息素的相對重要程度，其值越大，信息素的濃度在轉移中起的作用越大。 β為預見值的相對重要程度，其值越大，螞蟻以越大的概率轉移到接續時間較短的下一個乘務區段節點。其中預見度：

ηij=1ttij+（1-Eij）t1-Eijt2（25）

其中：ttij表示兩相鄰乘務區段接續弧的長度。Eij為0-1變量，Eij=1表示相接續的兩乘務區段同屬同一動車組交路，否則為0。t1為乘務人員換乘時間標準，t2為乘務人員在同車底上擔當不同乘務區段的最小間隔時間。預見度越大，螞蟻所能搜尋到最鄰近的節點的概率越大，也就是說，兩相鄰乘務區段之間的接續時長越短，兩乘務區段接續的概率越大。

②當第k只螞蟻位于原點時，選擇節點i作為下一個乘務大區段起點的概率為：

Pki=[τi]α·[ηi]β∑i∈Dl[τl]α·[ηl]β， Dl≠1

0，其他 （26）

其中：Dl為0-1變量，Dl=1時，表示乘務區段i被螞蟻選擇;否則，Dl=0。其中ηi為預見度，可由式（27）計算獲得：

ηi=tsurplus-teitsurplus-tdurationi+ρNnoN+1（27）

其中：tei表示乘務區段i的值乘結束時刻;tsurpius表示除乘務區段i外，其余乘務區段集合中最早結束值乘的乘務區段的結束時刻;tdurationi表示乘務區段i的值乘時長; ρ為可控參數，表示螞蟻能夠選擇到最快結束乘務區段的期望值;Nno表示在當前階段，尚未被選入任何乘務大區段的乘務區段的數量，N表示乘務區段的數量。式（27）表明，隨著迭代次數的增加，在沒有被選擇的乘務區段集合中，能夠較早結束的乘務區段越容易被選為乘務大區段的起點。

設置雙重策略狀態的轉移概率主要目的在于提高算法的全局搜索能力，防止其收斂于局部最優解，避免算法停滯或過早收斂。算法針對路徑選擇策略進行了改進，螞蟻從“原點”或“非原點”出發，根據相鄰乘務區段節點間的接續時間和接續狀態動態地調整啟發函數。當螞蟻所在的乘務區段節點i不是原點時，螞蟻以轉移概率Pkij（式（24））接續下一個乘務區段節點j，乘務區段節點距離目標節點越近則接續預見度ηij就越大。當螞蟻所在的乘務區段節點i不是原點時，螞蟻以轉移概率Pki（式（26））接續下一個乘務區段節點i，能夠較早結束的乘務區段越容易被選為乘務大區段的起點，即接續預見度ηi越大。這樣， 使算法在降低問題復雜性的同時，減少了算法搜索的盲目性，有效引導算法朝全局最優方向進行搜索;同時增加了螞蟻搜索路徑的多樣性，又使得更新的路徑具有隨機性，能夠有效避免算法過早地陷入局部最優，而進入停滯狀態。

5）終止策略。

螞蟻經過若干次搜索后，找到的解不再改變，且所有乘務區段都已經被乘務交路所遍歷時，算法終止。本文算法具體實現流程如下所示：

步驟1 令nc ← 0，k ← 1，初始化α、 β、 ρ、螞蟻數量、最大迭代次數等參數。

步驟2 將m只螞蟻隨機地放置在原點，構建一個n維向量Crew-section，n維向量Crew-section中的元素代表了所有的乘務區段，所有元素都為0-1變量。當某一元素為0時，表示該元素對應的乘務區段未被乘務大區段遍歷，否則為1。初始化向量Crew-section，令所有元素初態為0。

步驟3 螞蟻k以概率Pkj選擇下一個乘務大區段的起點，同時更新向量Crew-section，把被乘務交路遍歷過的乘務區段所對應元素取值為1。判斷向量Crew-section中的所有元素是否為1。若是，則令k ← k+1，若k>m則跳轉至步驟6;否則重復步驟3。對于螞蟻k，若Crew-section向量中仍有0元素，則進行下步。

步驟4 螞蟻k以概率Pkj為節點i向下一個乘務區段節點j轉移。同時更新向量Crew-section，把被乘務交路遍歷過的乘務區段所對應的元素取值為1。判斷Crew-section向量中的所有元素是否為1，若是，則令k ← k+1，若k>m則跳轉至步驟6，否則重復步驟3。對于螞蟻k，若Crew-section向量中仍有0元素，則進行下一步。

步驟5 若接續乘務區段的累計工作時長已達到乘務大區段的工作時間標準，則完成一個乘務大區段的構建，返回原點，跳轉至步驟3;若累計工作時間標準還沒有達到乘務大區段的時間標準，而連續工作時長已達上限，則調整乘務區段之間的接續時間標準，給乘務人員（組）增加調休時間，并返回步驟4;否則直接返回步驟4。

步驟6 當向量Crew-section中的所有元素返回值為1時，m個螞蟻已經生成了可行的乘務大區段回路。計算生成的乘務大區段的數量，并確定此次迭代產生最優解的螞蟻。

步驟7 根據式（20）和式（21）更新解構建圖中所有路徑和乘務區段節點上的信息素濃度。

步驟8 令nc ← nc+1，如果nc小于步驟1中指定的最大迭代次數，更新向量Crew-section，轉至步驟2;否則，終止計算，輸出當前最優解。

3 實例驗證及分析

3.1 實驗數據

為了驗證本文理論研究和算法的有效性，選取廣深線上城際列車數據進行驗證。廣深線起點廣州站，終點深圳站，全長147km，途經廣州、廣州東、東莞、常平、樟木頭、平湖、深圳7個車站，并辦理客運營業業務，周內每日開行73趟列車，周末每日開行95趟列車。動車組的檢修基地設置在廣州東站接軌的石牌動車檢修所。乘務基地設置在廣州東站，深圳站設乘務人員公寓，供在深圳駐班或調休的乘務班組休息。線路示意圖如圖1所示。

廣深線乘務運用情況說明：機務乘務組應遵循早出乘早下班、晚出乘外下班的出乘原則。所有乘務組在乘務基地進行出退乘作業，廣州東廣州乘務值乘方式為雙班單司機，廣州東深圳乘務值乘方式為單班單司機。廣深線乘務人員值乘方式如圖2所示。

現以廣深線6：00—24：00的城際列車開行方案數據為例。其中，有18對列車為廣州至深圳直達列車，57對列車為廣州東至深圳直達列車，以廣州東站為乘務基地，以深圳為換乘站，將廣深線城際列車開行方案數據劃分為150個乘務區段，如表2所示。

3.2 算例結果

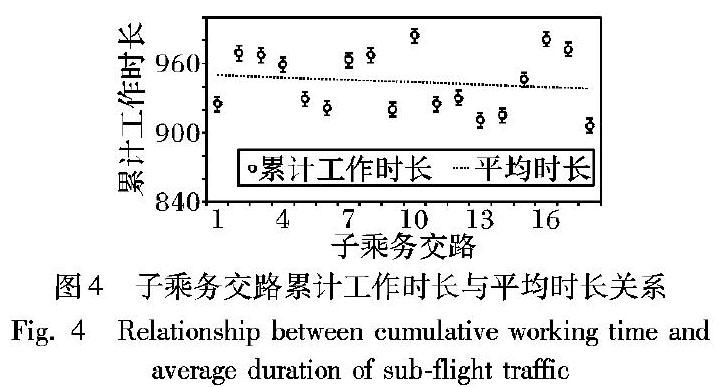
根據上文所述乘務規則約束，輸入乘務交路時間相關的參數，實驗參數可根據現場具體車站的乘務規則作出相應調整。根據廣深線調研數據可得，乘務交路相關時間參數設置為：乘務交路長度不超過2880min，換乘時間不少于12min，間休時間不少于為40min，連續值乘時間不超過300min，出乘時間60min，退乘時間20min。正整數M的取值為2880， ε取值為1（在正常情況下，根據乘務基地廣州東的歷史乘務數據，查定得到的數值）。運用本文設計的改進蟻群算法進行求解，其中：信息素重要程度因子α=2，啟發式信息素重要程度因子為5，信息素揮發因子取0.2，螞蟻個數取40，設迭代次數為300次。并運用Matlab R2015b進行求解，在Intel core i7-8550U CPU 1.8GHz，內存8GB的計算機上迭代到92次時，目標函數值已趨于穩定且達到最小，此時目標函數值為18452.71523min，迭代過程如圖3所示。共得到36條乘務大區段，如表3所示。得到18條子乘務交路，如表4所示。子乘務交路累計工作時長與平均時長關系如圖4所示，由圖4可看出子乘務交路間任務量較均衡。根據優化結果，可以看出乘務大區段有三種類型：①廣州東（廣州）廣州東，乘務大區段個數為18，占比50%;②廣州東深圳，乘務大區段個數有9，占比25%;③深圳廣州東，乘務大區段個數為9，占比25%。

3.3 實驗結果評價分析

利用設計了乘務交路時間較少、子乘務交路間乘務任務均衡為目標的優化模型和雙重策略蟻群算法，編制了廣深線

乘務交路計劃，計算結果的指標分析如表5所示。結論如下：

1）根據本文設計的基于雙重策略的蟻群算法，得到了18條乘務交路。乘務人員執行完一條乘務交路需要兩天時間。若乘務人員第一個工作日內早晨6點出乘，那么該乘務人員值乘當日最后一列車不超過14點，即早出乘，早退乘。

比如C7023次列車從廣州6：00始發，值乘這次列車的乘務人員就需要5：00從廣州東整備出勤，到中午12：41值乘完當天最后一列車退乘休息。充分保證了乘務人員的休息時間，使乘務人員有更多的時間學習業務知識，也利于照顧家人，大大提升了乘務人員的生活幸福指數。

2）從編制的18條乘務交路計劃中可看出，沒有發生超勞的情況，乘務人員單日最大值乘5列，并且在連續值乘4列后，乘務人員都有不少于40min的間休時間，使乘務人員有更充沛的精力值乘后續列車，有效地保障了列車運行安全。

3）在本文編制的乘務交路計劃中，充分考慮到人性化因素。比如每天有9對車底在深圳過夜，即每天必須有9個乘務組需要在深圳公寓休息。這9個乘務組都是從15：00以后出乘，即晚出乘，外下班。比如C7129次列車從廣州東18：11始發，直到乘務人員值乘完C7121最后一列車，在深圳站23：53退乘，乘務人員當晚在深圳公寓駐班休息。第二個工作日內，該乘務人員經過充分休息在12：18值乘C7038次列車從深圳始發，20：37值乘C7020從廣州東退乘。對于乘務人員來說，每值乘一條乘務交路都有充足的休息時間，體現了乘務交路編制過程中的人性化標準。

4）設計的目標函數既考慮了乘務交路總時長，又考慮了各子乘務交路之間的均衡性。如果某車站發生突發事件，比如深圳市某日要舉辦大型國際會展，客流激增的情況下，交路間的均衡性不再成為乘務交路編制的關鍵限制因素，此時重點考慮交路時長問題。根據乘務基地廣州東的歷史乘務數據，查定得到均衡因子取不同數值時目標函數值的變化，突發事件條件下，可根據乘務交路時長與均衡因子關系圖（如圖5）對均衡因子進行調整，Pkijε可根據實際需求設定相應較大的數值（如圖5），這種情況下乘務交路間的均衡性不再成為重要約束因素，以此來保證救援乘務組能夠快速機動地到達事故地點。

3.4 算法對比分析

多數學者在求解乘務計劃問題時多采用遺傳算法，因此，本文以遺傳算法作為對比算法。在同一臺計算機上運用Matlab R2015b求解，均衡因子取值與上相同，經過203次迭代后，結果趨于穩定，運行結果為19580.23793min。通過對比分析得，本文設計的改進蟻群算法與遺傳算法相比，能夠更快地收斂，解的質量也有大幅提升。其中，乘務交路減少了約21.74%、乘務總時長降低了5.76%、交路超勞率為0。兩種算法對比結果如表6所示。

4 結語

1）本文建立了總交路時間最小且各子乘務交路間任務均衡的MTSP模型，引入了均衡因子這一概念，使得模型更具備實際意義，在突發事件發生后更容易調整乘務交路計劃。同時提出了一種雙重策略狀態轉移的蟻群算法，其特點在于設計了雙重信息素、雙重策略，提高算法搜索效率的同時避免了傳統蟻群算法易陷入局部最優的缺點。

2）通過改進后的蟻群算法與遺傳算法相比，得出了本文設計的改進蟻群算法效率更高、解質量更好，對該問題求解有很強的適應性。

3）該模型及算法可為鐵路機務部門編制機車乘務人員乘務交路計劃提供有價值的決策支持，對增強鐵路機務系統應急處置能力具有實際意義和幫助，可作為鐵路系統應急處置決策理論的組成部分。

參考文獻

[1]BEASLEY J E， CAO B. A tree search algorithm for the crew scheduling problem [J]. European Journal of Operational Research， 1996， 94（3）： 517-526.

[2]CHU S C K. Generating， scheduling and rostering of shift crew-duties， applications at the Hong Kong International Airport [J]. European Journal of Operational Research， 2007， 177（3）： 1764-1778.

[3]DENNIS HUISMAN. A column generation approach for the rail crew re-scheduling problem [J]. European Journal of Operational Research， 2007， 180（1）： 163-173.

[4]GAMACHE M， HERTZ A， OUELLET J O. A graph coloring model for a feasibility problem in monthly crew scheduling with preferential bidding [J]. Computers and Operations Research， 2007， 34（8）： 2384-2395.

[5]陳海平.高速鐵路乘務組織理論與優化研究[D].北京：北京交通大學，2013：42-61.（CHEN H P. Research on theory and optimization of crew organization of high-speed railway [D]. Beijing： Beijing Jiaotong University， 2013： 42-61.）

[6]趙鵬，胡安洲，楊浩.機車乘務人員運用計劃的優化編制[J].鐵道學報，1998，20（4）：8-13.（ZHAO P， HU A Z， YANG H. Research on optimization of crew scheduling [J]. Journal of the China Railway Society， 1998， 20（4）： 8-13.）

[7]閻永光，黃斌.廣深線城際列車乘務組排班計劃編制方法探討[J].交通運輸工程與信息學報，2010，8（1）：25-29.（YAN Y G， HUANG B. Research on the crew schedule programming method of Guangzhou-Shenzhen intercity trains [J]. Journal of Transportation Engineering and Information， 2010， 8（1）： 25-29.）

[8]程巖巖.我國鐵路乘務調度計劃編制方法的研究與設計[D].北京：北京交通大學，2007：21-30.（CHENG Y Y. Research and design of domestic railway crew scheduling method [D]. Beijing： Beijing Jiaotong University， 2007： 21-30.）

[9]王瑩，劉軍，苗建瑞.客運專線乘務交路計劃編制的優化模型與算法[J].鐵道學報，2009，31（1）：15-19.（WANG Y， LIU J， MIAO J R. Modeling and solving the crew scheduling problem of passenger dedicated line [J]. Journal of the China Railway Society， 2009， 31（1）： 15-19.）

[10]王媛媛，周成晨，倪少權.基于蟻群算法的客運專線乘務交路計劃編制方法研究[J].鐵路計算機應用，2009，18（7）：11-14.（WANG Y Y， ZHOU C C， NI S Q. Study on algorithm of crew routing scheduling for passenger dedicated line based on ant colony optimization[J]. Railway Computer Application， 2009， 18（7）： 11-14.）

[11]黃珊.機車乘務人員運用問題及其輔助編排系統研究[D].長沙：中南大學，2014：30-44.（HUANG S. Locomotive crew scheduling problem and scheduling assistant system [D]. Changsha： Central South University， 2014： 30-44.）

[12]田志強.高速鐵路乘務計劃編制優化理論與方法研究[D].成都：西南交通大學，2011：45-72.（TIAN Z Q. Study on theory and methods of crew planning problem of high-speed railway[D]. Chengdu： Southwest Jiaotong University， 2011： 45-72.）

[13]陳旭，李海鷹，王瑩，等.放射狀路網條件下動車組運用優化研究[J].鐵道學報，2017，39（11）：1-7.（CHEN X， LI H Y， WANG Y， et al. Research on optimization of EMU scheduling for radial HSR network [J]. Journal of the China Railway Society， 2017， 39（11）： 1-7.）

[14]郭璞.鐵路客運機車乘務交路編制問題研究[D].長沙：中南大學，2013：24-32.（GUO P. Railway passenger train crew scheduling problem [D]. Changsha： Central South University， 2013： 24-32.）

[15]銀大偉.乘務計劃編制系統的研究與設計[D].成都：西南交通大學，2008：30-41.（YIN D W. Research and design of crew scheduling system [D]. Chengdu： Southwest Jiaotong University， 2008： 30-41.）

[16]張哲銘，王瑩，陳旭，等.高速鐵路單一循環乘務值乘計劃優化研究[J].鐵道運輸與經濟，2018，40（1）：21-27.（ZHANG Z M， WANG Y， CHEN X， et al. Research on single-circulation crew rostering plan optimization for high-speed railway [J]. Railway Transport and Economy， 2018， 40（1）： 21-27.）

[17]馬良，朱剛，寧愛兵.蟻群優化算法[M].北京：科學出版社，2008：57-73.（MA L， ZHU G， NING A B. Ant Colony Optimization Algorithm [M]. Beijing： Science Press， 2008： 57-73.）

[18]段海濱.蟻群算法原理及其應用[M].北京：科學出版社，2005：212-232.（DUAN H B. Ant Colony Algorithms： Theory and Applications [M]. Beijing： Science Press， 2005： 212-232.）

This work is partially supported by the National Key Research and Development Project of China （2016YFB1200100）， the National Natural Science Foundation of China （71861022， 61563028）.

WANG Dongxian， born in 1992，M.S. candidate. His research interests include operation management and decision optimization of rail transit.

MENG Xuelei， bon in 1979，Ph.D.，professor.His research interests include operation management and decision ayoptimization of rail transit.

QIAO Jun， born in 1993，M.S. candidate. Her research interests include operation management and decision optimization of rail transit.

TANG Lin， born in 1989，M.S. His research interests include operation management and dcision optimization of rail transit.

JIAO Zhizhen， born in 1992， assistant engineer. His research interests include organization and optimization of railway traffic， organization of cargo transportation.