基于值差度量和聚類優化的K最近鄰算法在銀行客戶行為預測中的應用

李博 張曉 顏靖藝 李可威 李恒 凌玉龍 張勇

摘 要：為提升貸款金融客戶行為預測的準確性，針對傳統的K-最近鄰（KNN）算法在數據分析中處理非數值因素的不完備問題，提出了一種采用值差度量（VDM）距離的對聚類結果迭代優化的改進KNN算法。首先對收集到的數據信息進行基于VDM距離的KNN算法的聚類，再對聚類結果進行迭代分析，最后通過聯合訓練提高了預測精度。基于葡萄牙零售銀行2008—2013年收集的客戶數據比較可知，改進的KNN算法與傳統的KNN算法、基于屬性值相關距離的KNN改進（FCD-KNN）算法、高斯貝葉斯算法、Gradient Boosting等現有算法相比具有更好的性能和穩定性，在銀行數據預測客戶行為中具有很大的應用價值。

關鍵詞：K-最近鄰算法;值差異度量距離;金融危機;行為預測;數據挖掘

中圖分類號：TP311.13

文獻標志碼：A

Application of KNN algorithm based on value difference metric and clustering optimization in bank customer behavior prediction

LI Bo1，2*， ZHANG Xiao1，2， YAN Jingyi3， LI Kewei1， LI Heng1，2， LING Yulong1，2， ZHANG Yong1，2

1.School of Computer Science， Northwestern Polytechnical University， Xian Shaanxi 710129， China;

2.Ministry of Communications Key Laboratory of Big Data Storage and Management （Northwestern Polytechnical University）， Xian Shaanxi 710129， China;

3.School of Management， Northwestern Polytechnical University， Xian Shaanxi 710129， China

Abstract：

In order to improve the accuracy of loan financial customer behavior prediction， aiming at the incomplete problem of? dealing with non-numerical factors in data analysis of traditional K-Nearest Neighbors （KNN） algorithm， an improved KNN algorithm based on Value Difference Metric （VDM） distance and iterative optimization of clustering results was proposed. Firstly the collected data were clustered by KNN algorithm based on VDM distance， then the clustering results were analyzed iteratively， finally the prediction accuracy was improved through joint training. Based on the customer data collected by Portuguese retail banks from 2008 to 2013， it can be seen that compared with traditional KNN algorithm， FCD-KNN （Feature Correlation Difference KNN） algorithm， Gauss Naive Bayes algorithm， Gradient Boosting algorithm， the improved KNN algorithm has better performance and stability， and has great application value in the customer behavior prediction from bank data.

Key words：

K-Nearest Neighbors （KNN） algorithm; Value Difference Metric （VDM） distance; financial crisis; behavior prediction; data mining

0 引言

在貸款金融領域，銀行機構營銷需要對用戶進行分析和分類，以降低營銷成本。基于某目標人群，從海量的其他人群中找出和目標人群相似的人群，以拓展目標人群規模。在現實生活中，通過海量數據集，并對數據劃分標簽，然后對用戶行為進行分析和分類，再進行相應的營銷手段，可以降低成本，并取得較好的效果[1-3]。當前的一些研究指出，銀行信息的數據挖掘不應該僅僅局限于會計數據，還需要考慮一些社會因素。

基于數據挖掘和用戶行為預測的目的，本文采用數據挖掘方法對葡萄牙銀行業金融機構直接營銷活動（電話）相關數據進行分析，通過電話營銷和電話銷售預測銀行長期存款的可能性。該數據集由葡萄牙零售銀行于2008—2013年收集，受到當時金融危機的影響，分類的目的是預測客戶是否會訂購定期存款。對于該數據集來說，主要的困難在于其特征的選擇，數據集中存在無用的或有噪聲的特征，這些特征可能會降低預測結果。基于這個目的，本文采用了一種改進的K-最近鄰（K-Nearest Neighbors， KNN）算法。KNN算法能夠更好地分析相似客戶的行為，更好地對客戶進行分類。傳統的

KNN算法存在一定的局限性。本文對距離計算和聚類分析方法進行了改進，實驗結果表明，改進的KNN算法在銀行數據挖掘中具有良好的預測效果。

1 研究現狀

數據挖掘是指通過數據過濾，從大量現有數據中搜索有趣的、有價值的數據點或數據模塊的數據處理技術。數據挖掘在商業金融領域有著廣泛的應用，根據商業分析的既定目標，可以通過企業內部的財務數據系統進行數據分析，以獲得所需的業務運營和市場發展規律，并可以通過成熟的數據挖掘模型和其他分析工具進行支持，形成了商業化的數據挖掘與分析系統。

2008—2013年，葡萄牙零售銀行業受到金融危機的影響，因此銀行需要分析數據挖掘，分析客戶是否可以繼續存款。根據社會心理學研究，當人們處于壓力狀態下時，往往有更多的本能表現，數據分析的準確性也會相應提高[4-5]。在金融危機期間，人們對金融投資都會持謹慎態度。另一方面，葡萄牙零售銀行業有著成熟的數據倉庫，對銀行客戶的個人數據、賬戶信息、交易歷史、業務服務歷史、財務管理數據、個人財務風險評估等進行了數據倉儲，可以對每個銀行客戶進行多維度的財務分析。

目前，對銀行客戶信息挖掘的研究較多，對銀行客戶信息挖掘的研究需求巨大。一些研究發現：配給大量信息的信貸員并沒有比配給少量信息的信貸員預測更準確，現有會計信息可能過量。因此當前的研究應該更多考慮考慮非數值指標，如：職業、學歷等。基于屬性值相關距離的KNN（Feature Correlation Difference-KNN， FCD-KNN）改進算法對非數值的因素進行了考慮：比較樣本間的距離為屬性值的相關距離，從而度量樣本間的相似度[6-7]。KNN算法是一種非常常見的算法，簡單易用，易懂，精度高，理論成熟;但也存在許多問題，為此人們提出了許多改進的K近鄰算法。為了解決銀行分類問題，本文采用了一種改進的KNN算法：用更適合銀行情況的搜索距離函數代替標準歐幾里得距離，用更精確的概率估計方法代替簡單的投票機制。實驗表明，本文提出的改進的K最近鄰KNN算法精度得到了很大的提高，是一種有效的算法，具有很好的推廣前景。

2 算法分析

2.1 傳統的KNN算法

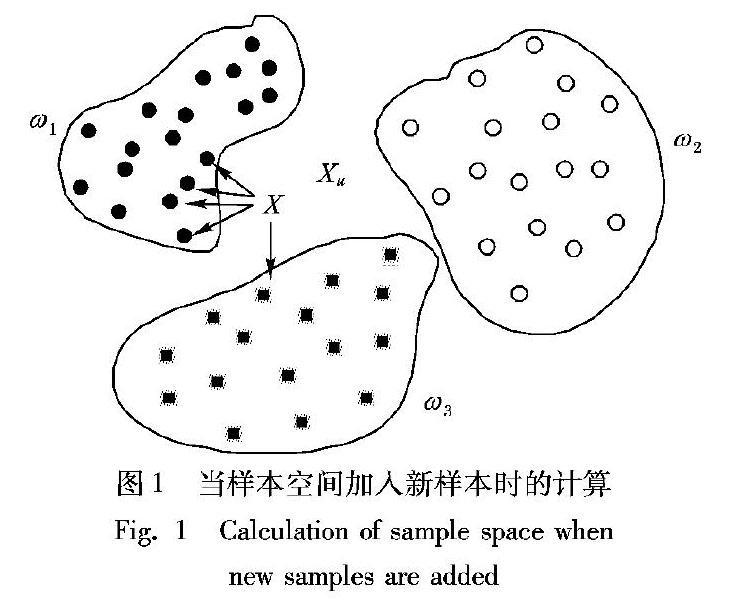
K-最近鄰（KNN）分類算法在模式識別領域得到了廣泛的應用。KNN算法基于類比學習，所有訓練基元都存儲在N維模式空間中。如果特征空間中k個最相似的樣本中的大多數屬于某個類別，那么這些樣本就屬于這個類別。KNN算法不僅可以用于分類，還可以用于回歸分析。通過尋找樣本的K最近鄰點，并將這些相鄰點的屬性平均值賦給樣本，可以得到樣本的預測值。例如，在圖1中，當一個新的樣本值添加到向量空間中時，在樣本值附近對其進行分析并進行分類。傳統的KNN算法得到了廣泛的應用，但鑒于銀行系統的特殊性，本文對距離選擇和判別法進行了改進，使分析預測更加準確，與傳統的KNN算法相比，其預測精度有了顯著的提高。

2.2 本文采用的改進KNN算法

針對銀行的特殊情況，本文采用了一種改進的KNN算法。改進措施包括：用更適合銀行業情況的搜索距離函數代替標準歐幾里得距離，用更精確的概率估計方法代替簡單的投票機制。

1）采用VDM距離修正。

距離計算是數據挖掘聚類的關鍵步驟。距離計算是計算采樣點與采樣點之間的距離，并根據計算結果判斷采樣點之間的關系。傳統的k-最近鄰KNN算法使用歐幾里得距離公式計算距離，例如：

ρ=（x2-x1）2+（y2-y1）2（1）

其中ρ為點（x1，x2）與點（y1，y2）之間的歐氏距離。

歐氏距離通常被用來本表示樣本的有序屬性，在本數據集中只有“年齡”符合這一條件。其他的條件如：婚姻狀況、工作類型等這樣的無序屬性，更適合采用值差度量（Value Difference Metric， VDM）距離。VDM距離是指： 令Mu，a表示在屬性u上取值為a的樣本數，Mu，a，i表示在第i個樣本簇中在屬性u上取值為a的樣本數，則屬性u上兩個離散值a與b之間的VDM距離為：

VDMp（a，b）=∑nii=1mu，a，imu，a-mu，b，imu，bp（2）

將歐氏距離和VDM結合可處理混合屬性。為不失一般性，令有序屬性排列在無序屬性之前，可得：

MinkowDMp（xi，xj）=（

∑ncu=1|xiu-xju|p+∑nu=nc+1VDMp（xiu，xju）

）1/p（3）

因為是在二維分析，可以p=2。無序屬性就是通過計算樣本簇中在屬性u上樣本點的多少來得到該樣本簇在該屬性上的“距離”。通過修正數據采集的距離，可以使得數據挖掘分析預測結果更為精確。

本文也探討了馬氏距離（Mahalanobis distance）在該問題下的應用，馬氏距離是對有序的、數值型的屬性，考慮其內在的關聯性，從而計算得出結果[8-9]。但是本文所提到的數據也有很多無序的屬性，使用馬氏距離處理會較為復雜，故未采用該處理方法。

2）對數據處理修正。

傳統的KNN方法對新增加的樣本點進行分類，使其具有更高的相似性。本文同時設置了各采樣點的屬性，并設置了劃分區域的閾值（比如：70%）。如果超出此閾值，本算法將把采樣點添加到一個沒有爭議的區域。如果點與每個區域之間的距離不明顯，本算法將該點標記為疑問點，在初步聚類結束后再考慮它。如圖2所示，如果點Xa與區域1（ω1）和區域2（ω2）之間的距離顯著不同，則將點Xa劃分為區域1。然而，在圖3中，例如，點Xb與區域1和區域2之間的距離沒有顯著差異。因此，點Xb暫時被標記為疑問點。

根據這種方法，最終會發現兩種類型的點：區域中心的無爭議點和區域邊緣的爭議點，如圖4所示。

在圖4中的情況，需要額外增加判斷過程，整體劃分，保留整個區域的最小離群值。甚至對于離群值邊緣太多，本算法可以將其劃分為新的區域或合并原始區域，即對分類結果又進行了一次處理。而對于圖5，如果區域外的點內部之間存在更多的相關性，即這一群爭議點彼此之間更為相似，如果用距離作標準，即這一群爭議點內部彼此之間的距離明顯小于它們與現有簇之間的距離（根據本文設置的閾值判斷）。首先可以通過在這些爭議點中隨機找到一個點，計算該點與其他爭議點之間的距離。如果發現其內部距離更小，則可以形成一個新的分類;甚至于其內部可能還會進一步的分裂，也可以進一步的處理。在圖5，中間的三個點彼此之間的距離更為接近（超過本文設置的閾值），可以直接增加新的分類，結果如圖6所示，這樣就有了更合理的集群。

3 實驗分析

為了驗證改進的K-最近鄰算法在銀行數據挖掘中的有效性，本文進行了實驗分析。選用的數據樣本是葡萄牙零售銀行在2008—2013年期間收集的數據樣本，將數據分為測試集和驗證集。數據預處理會有三種情況，分別為：未對原始數據作處理，將原始數據整為了應對實驗數據的噪聲合為符合正態分布，將原始數據整合到歸一化分布。同時為了比較算法的有效性，將傳統的KNN算法、FCD-KNN算法，高斯貝葉斯（Gaussian Naive Bayes）算法、Gradient Boosting 4種方法作為對照組實驗[10-11]。因此共進行了15組實驗，然后對實驗結果進行分析。

3.1 實驗數據處理

為了更為全面地分析數據，本文采用了3種數據預處理的方法，這三種方法各有利弊。本文會通過這5種算法的具體表現，驗證其穩定性和有效性。

3.1.1 未對原始數據作處理（只對數據標簽數字化）

在這種情況下，只對數據進行了預處理，分析數據本來之間的關系。具體步驟是：將原始數據的標簽進行數字化，具體是按序1，2，3的進行轉化，“no”是1，“yes”是2，null是3。不進行其他轉換，然后進行實驗分析。這種情況下，保持了數據的基本特性，但數據中的奇異點可能會對實驗精度有較大影響，從而降低一些依賴數值關系算法的精度，如：K-最近鄰算法。

3.1.2 將數據標準化成符合正態分布

大部分的數據分析都希望原始數據是滿足正態分布的定距變量，這樣數據分析更為精確，也會降低數據分析的復雜度。數據標準化調整是非常有用的。許多機器學習算法在具有不同范圍特征的數據中呈現不同的學習效果。例如，Gaussian Naive Bayes在沒有標準化調整過的數據中表現很差，因為可能一個變量的范圍是0～10000，而另一個變量的范圍是0～1。因此，對數據預處理符合正態分布，是一種有效的分析手段。將數據處理為符合正態分布的公式為：

z=（x-μ）/σ（4）

其中： μ、σ分別為原始數據集的均值和方法。該種歸一化方式要求原始數據的分布近似為高斯分布，否則歸一化的效果會變得很糟糕。本文首先對原始數據進行了分析，發現其大致符合高斯分布，符合將數據正態分布化的先決條件。通過這種方式，可以使數據規范化，同時使數據分析更為簡單。

3.1.3 將數據進行歸一化到[0，1]

對原始數據進行標簽數字化后，再對數據進行線性函數歸一化。利用線性函數將原始數據線性化的方法轉換到[0，1]的范圍，歸一化公式如下：

Xnorm=（X-Xmin）/（Xmax-Xmin）（5）

該方法實現對原始數據的等比例縮放，其中Xnorm為歸一化后的數據，X為原始數據，Xmax、Xmin分別為原始數據集的最大值和最小值。通過這種方法可以避免奇異點對數據分析造成的影響，但是會對數據的完整性和對比度造成影響。

3.2 實驗流程

本文使用Eclipse3+Python3+pydev的開發環境，也可以使用Java開發環境（JDK1.8以上），進行仿真模擬實驗。一共做12組實驗，隨機選取樣本集的70%為訓練集，30%為測試集，先對處理后訓練數據進行訓練，然后再在測試集上進行訓練，最后根據預測的精度來驗證實驗。

3.3 實驗結果

1）未對數據進行預處理的精度情況。

當未對數據進行預處理時（僅對標簽進行數字化），Gaussian Naive Bayes和Gradient Boosting算法表現的并不是特別理想，相比之下3種KNN算法的準確性更好，FCD-KNN算法作為一種較新穎的算法在這種情況下表現略優于于本文提出的改進KNN算法。未對數據進行預處理時，實驗結果如表1所示。

2）對數據預處理標準化成正態分布的精度情況。

根據KNN算法的特性，KNN算法一般會很好地處理奇異點（比如：不歸類），而本文改進的KNN算法會盡可能得將數據進行合理的分類;相比于FCD-KNN算法，對數據分類進行了進一步的處理，從而在銀行數據分析預測中有更好的表現。對數據預處理標準化成正態分布時，實驗結果如表2所示。

3）對數據預處理歸一化到[0，1]的精度情況。

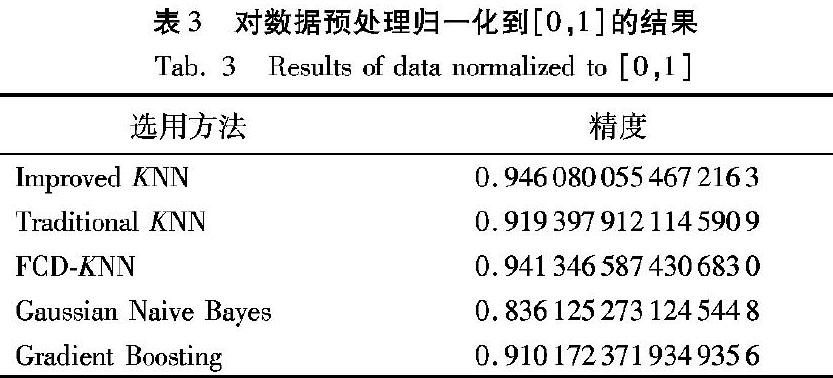
相比于對數據進行正態化分布預處理的情形，對數據進行歸一化處理得到的結果很相似。歸一化后加快了梯度下降求最優解的速度。同時，如果一個特征值域范圍非常大，那么距離計算就主要取決于這個特征，從而與實際情況相悖（比如這時實際情況是值域范圍小的特征更重要）。這種方法非常適用于采用距離判斷的K-最近鄰算法 ，通過這種方法，雖然此時5種預測算法的精度都有所下降，但是3種KNN算法還是明顯優于其他2種算法，同時改進的KNN算法略優于其他兩種的KNN算法。對數據預處理歸一化到[0，1]時，實驗結果如表3所示。

3.4 整體實驗結論分析

在整體結果中，本文提出的改進的KNN方法和FCD-KNN算法表現更好，說明本文提出的改進的KNN算法有一定的研究價值。分析原因，銀行用戶數據集不適合進行標準化，其噪聲可以通過SVM的RBF核函數的處理，RBF將數據集映射到高維上進行分類，從而有效減少了噪聲的影響，在低維上進行計算。進一步的展望是先進行聚類算法，假設噪聲都是一些離群點，將識別出來的很小的集合劃為噪聲，從而將噪聲識別出來并剔除，進一步提高精度。改進的KNN方法采用了VDM距離法，而樣本集中很多無法數字化比較的標簽（如婚姻狀態、工作狀態等）很難作為數字因素考慮。FCD-KNN算法也是對非數值的指標進行了考慮，但是本文提出的改進的KNN算法在數據分類過程中有更多的考慮，對實驗結果產生了一些有利的結果。

而Naive Bayes方法相比于其他方法精度較低，原因可能是：1）樸素貝葉斯方法需要先知道先驗分布和數據來決定后驗的概率從而決定分類，所以分類決策存在一定的錯誤率;2） 理論上，樸素貝葉斯模型與其他分類方法相比具有最小的誤差率。但實際上，因為樸素貝葉斯模型假設屬性之間相互獨立，這個假設在實際應用中往往是不成立的，在屬性個數比較多或者屬性之間相關性較大時，分類效果不好。

分析原因，可能是數據集中樣本的屬性之間有聯系，分析銀行客戶資料，“工作類型”“教育”“住房”“貸款”等屬性之間都可能會有聯系，所以這也是Naive Bayes方法精度比其他三種方法更低的原因。

3種KNN方法在三組實驗中均有優秀的實驗結果，精度均在0.92左右或以上，預測精度都非常穩定。整體實驗結果為：在不同預處理方式的之間，不標準化（僅對標簽數字化）>對數據預處理正態分布化>對數據預處理線性函數歸一化。因為在本次數據集，標簽并沒有太多的數值關系，因此使用歐氏距離傳統的KNN方法精度會下降，而采用VDM距離的改進的KNN方法和FCD-KNN方法均有突出的表現。而綜合三種情況分析，本文提出的改進的KNN方法無疑是在銀行數據挖掘分析預測中表現作為優秀和穩定的算法，其對于距離計算和聚類方式的改變，非常適用于銀行情況，因此具有很大的潛力。

4 結語

在大數據的背景下，對數據進行充分分析，可以減少實際工作中的成本。在金融行業對客戶的分析預測顯得尤為重要，數據分析聚類，可以給客戶提供相應的個性化服務。本文所提出的改進的K-最近鄰算法，對傳統的K-最近鄰算法進行距離計算和聚類方式的改變，通過實驗分析與數據驗證，以2008—2013葡萄牙銀行數據作為樣本集和測試集，對該算法進行驗證，取得了非常理想的計算結果。與目前主流的其他算法相比，具有更好的穩定性和精確性，該算法在金融數據分析方面有良好的效果，有樂觀的應用前景。

本文未來還會做以下工作：

1）本文研究的是處于金融危機下的人群，從社會學角度，這一時期的人群處于敏感時期，理財行為更為謹慎，因此要考慮本文研究的價值。

2）對數據的預處理是通常的數據挖掘中采用的手段，本文所提到數據預處理手段都較為簡單，本文會未來嘗試更多的預處理手段，使預測度更為精確。

參考文獻

[1]GUO J Y， WANG X， LI Y. kNN based on probability density for fault detection in multimodal processes [J]. Journal of Chemometrics， 2018， 32（7）： e3021.

[2]FEKI-SAHNOUN W， NJAH H， HAMZA A， et al. Using general linear model， Bayesian networks and Naive Bayes classifier for prediction of Karenia selliformis occurrences and blooms [J]. Ecological Informatics， 2018，43： 12-23.

[3]SAINI I， SINGH D， KHOSLA A. QRS detection using K-Nearest Neighbor algorithm （KNN） and evaluation on standard ECG databases [J]. Journal of Advanced Research， 2013， 4（4）： 331-344.

[4]職為梅，張婷，范明.基于影響函數的k-近鄰分類[J].電子與信息學報，2015，37（7）：1626-1632.（ZHI W M， ZHANG T， FAN M. k-nearest neighbor classification based on influence function [J]. Journal of Electronics and Information Technology， 2015，37（7）： 1626-1632.）

[5]宓文斌.數據挖掘在銀行信貸業務中的應用[D]. 上海：上海交通大學，2012.（MI W B. Application of data mining in the bank credit [D]. Shanghai： Shanghai Jiao Tong University， 2012.）

[6]JIANG L， CAI Z， WANG D，et al. Survey of improving k-nearest-neighbor for classification [C]// Proceedings of the 4th International Conference on Fuzzy Systems and Knowledge Discovery. Piscataway， NJ： IEEE， 2007： 679-683.

[7]肖輝輝，段艷明.基于屬性值相關距離的KNN算法的改進研究[J].計算機科學，2013，40（S2）：157-159.（XIAO H H， DUAN Y M. Improved the KNN algorithm based on related to the distance of attribute value [J]. Computer Science， 2013， 40（S2）： 157-159.）

[8]周治平，苗敏敏.改進的馬氏距離動態時間規整手勢認證方法[J]. 計算機應用，2015， 35（5）： 1467-1470.（ZHOU Z P， MIAO M M. Dynamic time warping gesture authentication algorithm based on improved Mahalanobis distance[J]. Journal of Computer Applications， 2015， 35（5）： 1467-1470.）

[9]de MAESSCHALCK R， JOUAN-RIMBAUD D， MASSART D L. The Mahalanobis distance [J]. Chemometrics and Intelligent Laboratory Systems， 2000， 50（1）： 1-18.

[10]TAHERI S， MAMMADOV M. Learning the naive Bayes classifier with optimization models [J]. International Journal of Applied Mathematics and Computer Science， 2013， 23（4）： 787-795.

[11]BIAU G， CADRE B， ROUVIRE L. Accelerated gradient boosting [J]. Machine Learning， 2019， 108（6）： 971-992.

[12]楊朔，陳麗芳，石瑀，等.基于深度生成式對抗網絡的藍藻語義分割[J].計算機應用，2018，38（6）：1554-1561.（YANG S， CHEN L F， SHI Y， et al. Semantic segmentation of blue-green algae based on deep generative adversarial net [J]. Journal of Computer Applications， 2018， 38（6）： 1554-1561.）

This work is partially supported by the National Key Research and Development Program of China （2018YFB1004401）.

LI Bo， born in 1994， M. S. candidate. His research interests include cloud storage， data mining.

ZHANG Xiao， born in 1978， Ph. D.， associate professor. His research interests include storage system.

YAN Jingyi， born in 1993， M. S. Her research interests include technology innovation management.

LI Kewei， born in 1993， M. S. candidate. His research interests include data mining.

LI Heng， born in 1993， M. S. candidate. His research interests include data mining.

LING Yulong， born in 1995， M. S. candidate. His research interests include data mining.

ZHANG Yong， born in 1995， M. S. candidate. His research interests include data mining.