基于SOC-OCV曲線特征的SOH估計方法研究

劉軼鑫，張 ，李 雪，韓智強

（1.中國第一汽車股份有限公司新能源開發院電池研究所，長春 130000； 2.北京新能源汽車股份有限公司，北京 100176）

前言

鋰離子電池在交通和儲能領域起到了重要的作用［1-4］。鋰離子電池狀態（如SOC和SOH等）的估計是確保鋰離子電池被合理使用的基礎。在過去10年里，SOC估計已經被廣泛研究并取得了突破性的進展［5-8］，但衡量電池老化和健康程度的SOH卻沒有引起足夠的重視。

SOH除了能夠體現鋰離子電池相對初始狀態下的最大能量存儲能力和功率輸出能力［9］，還一定程度上反映了電池的安全性能，如SOH較低時，電池的失效概率會顯著增加［10］。因此合理、準確地估計SOH對于新一代BMS至關重要。

SOH估計通常基于電池的容量或內阻［11-13］，SOH的估計方法主要可分為兩大類，一類是基于衰退機理的電化學模型［14-15］，另一類則是將智能算法與大數據相結合的SOH估計方法［16-21］。基于衰退機理的電化學模型要求準確理解電化學過程并運用電化學方程對SOH進行估計，這類模型需要對電化學反應過程進行簡化、對邊界條件進行一些合理假設。這類方法不僅計算非常繁瑣，且精度嚴重依賴于電池的老化路徑，因此，該方法很難在BMS系統中得到運用。而將智能算法和大數據相結合的SOH估計方法由于不需要理解復雜的電池老化過程且計算量相對較小而被廣泛研究：Lin等［18］使用了一種基于概率密度神經網絡的方法估計鈷酸鋰電池的SOH，在恒流充放電的循環工況下，SOH的平均估計誤差為0.28%，標準差為1.15%；He等［19］應用動態貝葉斯網絡估計錳酸鋰電池的SOH，在較大的溫度范圍和倍率條件下，SOH的估計誤差小于5%。但在電動車實際使用過程中，循環工況往往比上述研究中的恒流充放電工況更加復雜；與此同時，電池的老化路徑和工況是密切相關的。因此這些方法運用在實際BMS中難以保證SOH的估計精度。

為解決上述問題，本文中提出一種基于電池熱力學特性的SOH估計方法，主要有3個優勢：（1）電池熱力學表現和SOH的關系可通過少量實驗數據量化，使得精確在線估計SOH成為可能；（2）基于電池熱力學特性的SOH估計方法可在沒有電化學方程的情況下反映出電池的衰退機理；（3）SOH估計的準確度不受老化路徑影響。

1 SOC-OCV模型

本文中所用實驗樣品電池的SOC-OCV曲線如圖1（a）所示。這條曲線的單調趨勢是：（1）在SOC高端（SOC＞0.9），OCV急劇上升；（2）在 SOC中間區段（0.3＜SOC＜0.9），OCV近似線性增加；（3）當SOC處于低端（SOC＜0.3），OCV又急劇下降。實驗樣品電池的SOC-OCV曲線特性與錳酸鋰電池的特性相似，因此，錳酸鋰電池的SOC-OCV曲線的模型也可以用來分析本文的實驗樣品電池的SOC-OCV曲線特性［22］，如式（1）所示。

式中：y為 OCV；s為 SOC；a，b，c和 d為待確定的SOC-OCV曲線的特征參數。

采用最小二乘法對圖1（a）中的SOC-OCV實驗數據（即實線）進行辨識，可得 a＝3.81，b＝0.022，c＝0.31，d＝0.07。將這 4個參數值和 SOC值帶入式（1）可得OCV的計算值，如圖1（a）中的虛線所示。在典型的 SOC工作區間［0.1，0.9］，SOC-OCV曲線的模型相對誤差在0.4%左右，如圖1（b）所示。

由式（1）可知，SOC-OCV曲線的特征參數a和c表征了該曲線的線性部分，而特征參數b和d分別描述了該曲線的低端和高端部分。

圖1 SOC-OCV曲線的實驗值與模型值

2 SOC-OCV曲線特征參數衍變規律

2.1 實驗

本文中實驗樣本電池的正極是由錳酸鋰和鎳鈷錳三元材料組成的復合電極，負極材料是石墨，其中錳酸鋰與鎳鈷錳三元材料的比例是7∶3，樣本電池的額定容量是35 A·h。老化實驗及SOC-OCV測試實驗是由專業電池單體充放電設備（Arbin公司的BT2000）完成的，該充放電設備的最大電流輸入輸出能力是400 A，電壓范圍是0～5 V。

本文中利用容量增量（incremental capacity，IC）法畫出實驗樣本電池以C/20的電流倍率（其中1C表示以1C電流倍率將電池從電量為零充電至電量為100%需要1 h）充電的IC曲線如圖2所示，實驗樣本電池的IC曲線有3個峰，分別對應的SOC是10%，45%和80%。因此以20%和60%的SOC為間隔點可以將電池SOC使用區間分為3段。

圖2 電池的IC曲線

實驗樣本是相同批次的6支電池，2支電池（編號為#1和#2）在SOC區間［0，20%］下執行老化工況實驗，2支電池（編號為#3和#4）在SOC區間［20%，60%］下執行老化工況實驗，1支電池（編號為#5）在SOC區間［60%，100%］下執行老化工況實驗，1支電池（編號為#6）在SOC區間［0，100%］下執行老化工況實驗。這樣安排實驗的目的是分析電池老化對路徑的依賴情況：編號為#1和#2，#3和#4的電池所做的老化實驗是為了對比分析電池相同老化路徑下，電池的老化狀態有無差異；編號為#1，#3，#5和#6的電池所做的老化實驗是為分析不同老化路徑對電池老化狀態的影響。老化工況設定為：在40℃下，電池在提前設定的SOC區間持續進行2C的充放電循環實驗。電池每執行完等效的100次完整充放電循環測試一次SOC-OCV曲線，對應上述4個區間老化實驗的循環數分別為500，250，250和100次。SOC-OCV曲線測試的方法是：在SOC的高端和低端，每隔5%的SOC對OCV進行測量，而在SOC中間部分，每隔10%的SOC對OCV進行測量，采用1C/3倍率充電對SOC進行調整，每個充電片段結束后靜置2 h，再開始下一個充電片段，靜置2 h之后的電池電壓作為電池的開路電壓OCV。

2.2 SOC-OCV曲線及其特征參數的衍變趨勢

從圖3可以看出，在相同老化路徑下，#1號電池和#2號電池的SOC-OCV曲線變化情況一致，而#3號電池和#4號電池的SOC-OCV曲線變化情況不同，而不同的老化路徑下，例如#1號電池，#3號電池，#5號電池和#6號電池的SOC-OCV曲線變化情況完全不同，所以在相同的容量吞吐量的情況下，電池的健康狀態并不相同。圖3中的循環次數是等效成完整充放循環之后的數值。

圖3 SOC-OCV曲線隨老化的變化

利用最小二乘法辨識出SOC-OCV曲線的特征參數a和c，隨老化的變化趨勢如圖4所示，在電池老化過程中，特征參數a增大，而特征參數c減少。

3 SOH計算

3.1 老化機理分析

本文中采用IC分析法分析SOC-OCV曲線特征參數與電池老化之間的關系，圖5給出了#6號電池的IC曲線，圖中有兩個明顯的 IC峰，處于3.8與4.2 V之間。錳酸鋰作為正極材料，有兩個電壓平臺，分別為4.1和3.95 V，對應兩個相變過程，因此圖5中的IC峰是錳酸鋰材料與石墨負極反應形成的。而鎳鈷錳三元材料的IC峰對應的電壓平臺在3.75 V附近，但在圖5中此峰并不明顯，主要原因是該材料的占比低導致的。另外，由于圖5的IC曲線是基于實驗過程中的SOC-OCV曲線獲得，由于該曲線的SOC間隔比較大，也會導致鎳鈷錳三元材料的IC峰不明顯，這也解釋了相同批次電池的IC曲線有一些差異（如圖5和圖2所示）。

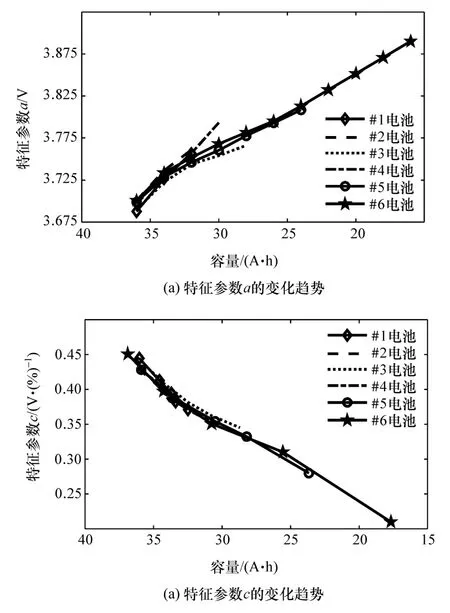
圖4 特征參數a和c隨老化的衍變趨勢

當電池老化之后，粒子轉移能力下降，導致電池的內阻增加和動力學下降，圖5中IC曲線隨老化向高電位平移也證明了這點。為了探索SOC-OCV曲線特征參數與電池老化之間的內在關聯，本文中提取圖5中兩個明顯 IC峰之間的電壓差，如表1所示。

圖5 #6電池的IC曲線

從表1可以看出，隨著電池老化，兩個IC峰之間壓差在縮小，SOC-OCV曲線特征參數a逐漸增加，而SOC-OCV曲線特征參數c逐漸縮小，電池老化，電池內阻在增加，電池動力學性能在下降，因此SOC-OCV曲線特征參數a和c的變化趨勢能間接反映電池內阻及動力學性能的變化過程。

表1 SOC-OCV曲線特征參數與IC峰之間電壓差的關系

圖6給出了6支電池的SOC-OCV曲線特征參數a和c隨電池容量衰退的變化趨勢，清晰表明SOC-OCV曲線特征參數a和c與電池衰退之間存在很強相關性。基于上述分析，SOC-OCV曲線特征參數a和c能夠反映出電池的衰退機理，也可以作為SOH的表征因子。

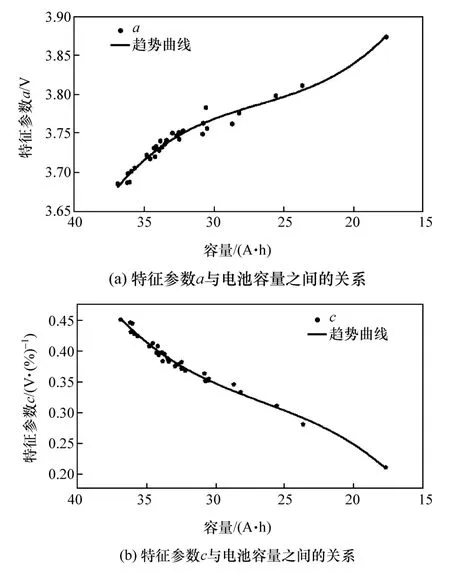
圖6 SOC-OCV曲線特征參數a和c與電池衰退之間的相關性

3.2 SOH計算

為有充分的數據對SOH建模并驗證SOH模型的精度，將實驗樣品電池分為兩組，一組包含5支電池，作為模型訓練組，一組包含1支電池，作為模型精度驗證組。#5電池的老化速率比較溫和，既不是容量衰退最快的，也不是容量衰退最慢的，因此#5電池老化數據用來驗證SOH模型的精度，其余電池作為模型訓練數據。本文中將電池容量的衰退作為電池的SOH真值：

（1）用特征參數a來表征SOH

SOH變化趨勢與特征參數a的衍變趨勢如圖7（a）所示，y軸為SOH值，x軸為特征參數a。由圖可見，隨著特征參數a的增加，SOH呈現明顯的遞減趨勢，而且遞減趨勢不符合拋物線特征，因此選用3階多項式來擬合SOH與特征參數a之間的關系：

為了評估式（3）的精度，將SOH模型值與真值之間作差，得到誤差曲線如圖8的虛線所示。由圖可見，SOH從100%下降到50%，SOH的估計精度在-3.5%～2.5%之間。

（2）用特征參數c來表征SOH

SOH變化趨勢與特征參數c的衍變趨勢如圖7（b）所示。由圖可見，隨著特征參數c的增加，SOH呈現明顯非線性遞增趨勢，而且遞減趨勢也不符合拋物線特征，因此也選用3階多項式來擬合SOH與特征參數c之間的關系：

為了評估式（4）的精度，將SOH模型值與真值之間作差，得到誤差曲線如圖8的實線所示。由圖可見，SOH從100%下降到50%，SOH的估計精度在±1.5%以內。

基于以上分析，SOC-OCV曲線特征參數a和c都可以用來表征SOH，但是式（3）的擬合系數很大，特征參數a發生很小的抖動會給SOH的估計結果帶來很大的偏差，因此，將特征參數a作為SOH的表征因子有很大的風險。考慮到SOH的估計精度，式（4）的擬合系數是可以接受的。因此，本文基于SOC-OCV曲線特征參數c提出了表征SOH變化的表達式：

式中α，β，γ和C為依賴于電池正負極材料的化學特性的系數。

圖7 SOH與SOC-OCV曲線特征參數之間的關系

圖8 SOH估計模型精度

3.3 驗證

采用#5號電池來驗證提出的SOH表達式的精度。由于#5電池與模型訓練組的電池是同一批電池，電池的材料屬性一致，因此采用式（4）來計算SOH的模型值，該值與SOH真值的差如圖9所示。可以看出，SOH從98%下降到65%，SOH的估計精度在±1.5%以內。

4 結論

通過跟蹤SOC-OCV曲線特征參數的衍變規律，本文中提出了一種行之有效的SOH估計方法，主要有以下3方面優勢：

圖9 #5號電池的SOH估計精度

（1）較高的SOH估計精度，對于本文中研究的復合電極體系的電池，SOH從100%衰退到50%，SOH估計精度在±1.5%以內；

（2）不依賴于老化路徑，在不同老化路徑下得到的特征參數c有幾乎相同的衍變規律，因此SOH的估計精度與老化路徑無關；

（3）能夠反映老化機理，隨著電池老化，特征參數c發生不同程度的減小，與電池動力學性能的衰退趨勢相同，能夠定性的表征電池的老化機理。