七溝道球籠式等速萬向節(jié)磨損及仿真分析*
謝 鯤,劉征宇,郭常寧,閆公哲,石寶樞
(1.上海應用技術大學軌道交通學院,上海 201418; 2.上海交通大學機械與動力工程學院,上海 201400;3.華東理工大學機械與動力工程學院,上海 200237; 4.浙江眾達傳動股份有限公司,金華 321025)
前言
球籠式等速萬向節(jié)可以實現(xiàn)輸入軸和輸出軸存在夾角時的等角速度傳動,其載荷是星形套端輸入軸通過星形套內溝道橢圓曲面?zhèn)鬟f給鋼球球面,再由鋼球球面?zhèn)鬟f給鐘形殼外溝道橢圓曲面,而到達鐘形殼端輸出軸的轉矩和回轉運動。鋼球、星形套、保持架、鐘形殼這幾個主要部件的受力過程是輸入轉矩傳遞的關鍵,鋼球與星形套、保持架、鐘形殼在傳遞轉矩過程中的法向接觸力、摩擦力可作為球籠式等速萬向節(jié)部件間的磨損量和疲勞壽命的理論依據。
目前國內外對于球籠式等速萬向節(jié)的內部受力及摩擦磨損的研究并不多見。文獻[1]中通過三維重構技術搭建了球籠式等速萬向節(jié)的三維模型,并對其承受極限轉矩時的內部接觸應力進行有限元分析,最后對比兩種極限工況的數值解;文獻[2]中通過對七溝道球籠式等速萬向節(jié)星形套和鐘形殼圓弧形溝道曲率的解析,根據Hertz接觸理論分別計算出溝道與鋼球接觸時的接觸應力,進而探討該類萬向節(jié)優(yōu)化設計的規(guī)律;文獻[3]中對球籠式萬向節(jié)內外滾道接觸應力進行了有限元分析,得出內滾道的接觸應力明顯大于外滾道,內滾道更容易受到破壞。但是,鋼球在傳遞運動和轉矩的過程中產生的摩擦力,以及由摩擦力產生的軸向竄動力、徑向力、偏轉轉矩卻很少有人研究,這些力的變化會直接影響萬向節(jié)的磨損-疲勞壽命,而且其研究結果將對以后研究分析萬向節(jié)內部的摩擦磨損有著非常重要的理論指導意義。
鑒于此,本文中通過鋼球在溝道內的瞬時角速度和星形套內溝道鐘形殼、外溝道與鋼球接觸點的瞬時角速度,計算鋼球在溝道內的瞬時滑滾比,以此判斷鋼球在溝道內的滑滾移動狀態(tài),從而計算并分析鋼球與星形套、鋼球與保持架的摩擦力,得到了摩擦力隨著輸入端角速度、輸入端對輸出端擺角的變化規(guī)律,同時根據Archard磨損理論,對球籠式等速萬向節(jié)進行磨損分析。
1 受力模型
圖1為鋼球在萬向節(jié)內的受力模型。由圖可知球籠式等速萬向節(jié)一個鋼球在一組星形套內溝道、鐘形殼外溝道和保持架窗口作用下的受力情況。鋼球的球心O及其所在坐標系ρQ=[];當星形套端輸入軸IN與鐘形殼端輸出軸IW之間的軸間擺角為2θ時,作為星形套和鐘形殼之間傳遞動力的關鍵部件,鋼球收到星形套內滾道和鐘形殼外滾道的周向力作用,此力使鋼球把星形套內滾道傳遞的動力帶給鐘形殼外滾道;鋼球與星形套和鐘形殼接觸點分別為N和W,在此兩點鋼球的法向接觸力分別為QNQi和QWQi,有此兩個法向接觸力而產生的摩擦力分別為fNQi和fWQi。除了與星形套內滾道和鐘形殼外滾道接觸以外,鋼球還始終與保持架相接觸,在保持架窗口的上下面分別對鋼球有法向接觸力QJQi以及由此法向接觸力產生的摩擦力fJQi。球籠式等速萬向節(jié)在其運動過程中,各個鋼球的瞬時受力,不論是法向接觸力 QNQi(QWQi),QJQi或是摩擦力 fNQi(fWQi),fJQi,都不是一成不變的,而是隨著轉角δ和星形套端輸入軸IN與鐘形殼端輸出軸IW之間的軸間擺角2θ的變化而不斷改變的。

圖1 鋼球受力模型
2 滑滾比S的數學模型
在球籠式等速萬向節(jié)的星形套端輸入軸IN旋轉一周的過程中,各個鋼球在星形套內溝道和鐘形殼外溝道內做純滑動、純滾動或者滑滾結合的運動,借助滑滾比可以明確鋼球在溝道內的具體運動形式。滑滾比是指在工程應用當中,零件滑動摩擦與滾動摩擦的比值,滑滾比S為

式中:v1為接觸部件1在接觸點處的瞬時線速度;v2為接觸部件2在接觸點處的瞬時線速度。若求得的S=0,則兩部件在接觸時做純滾動運動,若求得的S=2,則兩部件在接觸時做純滑動運動,若S∈(0,2),則兩部件在接觸時做滑滾結合運動。
鋼球中心OQ的旋轉角速度ωQ[2]為

由式(1)和式(2)可得出鋼球與星形套(或者鐘形殼)的滑滾比計算公式,并可以此作為判斷鋼球在星形套內溝道和鐘形殼外溝道內的摩擦為何種形式。
在球籠式等速萬向節(jié)中:

由式(3)和式(4),可得滑滾比 S為

圖2為滑滾比S隨轉角δ和軸間擺角2θ的變化規(guī)律。當鋼球與星形套內溝道和鐘形殼外溝道曲面的接觸角α=45°時(后面的討論都基于該條件),滑滾比S與轉角δ和軸間擺角2θ的函數關系曲線。由圖2可知,滑滾比S隨著轉角δ在一個周期的旋轉內呈周期性變化,隨著軸間擺角2θ的增大而減小,并始終滿足S∈(0,2),可以判斷鋼球在星形套內溝道和鐘形殼外溝道內做著滾滑結合的摩擦運動。軸間擺角越大,滾動摩擦占到的比重越大,滑動摩擦占到的比重越小,軸間擺角為0°~35°的過程中,滾動摩擦與滑動摩擦的比下降,說明軸間擺角越大,鋼球在星形套內溝道和鐘形殼外溝道內運動過程中的滑移越少;軸間擺角為0°時,鋼球在溝道內的位置始終相對保持不變,因此滑滾比也保持不變;軸間擺角為35°時,滑滾比隨著鋼球的往復運動而呈周期性變化[4-5]。

圖2 滑滾比S隨轉角δ和軸間擺角2θ的變化規(guī)律
圖3 為軸間擺角為35°時,滑滾比S隨鋼球與最外端距離L的變化規(guī)律。由圖3可知,鋼球運動到最外端時其滑滾比最大,運動到最內端時其滑滾比最小,滑滾比大的位置也是相對最容易出現(xiàn)磨損甚至是失效的位置。
圖4為軸間擺角2θ為35°時滑滾比隨轉角和偏心距的變化規(guī)律。由圖4可知,偏心距越大滑滾比也越大,在設計過程中選擇合適的偏心距對球籠式等速萬向節(jié)的性能也起到較大的影響。

圖3 滑滾比S隨轉角δ(溝道各位置)的變化規(guī)律

圖4 軸間擺角2θ為35°時滑滾比隨轉角和偏心距的變化規(guī)律
3 鋼球與星形套內溝道之間的摩擦力
由滑滾比S始終滿足S∈(0,2)的計算結果,得出鋼球在星形套內溝道和鐘形殼外溝道內做著滾滑結合的摩擦運動的結論,可借此進一步計算球籠式等速萬向節(jié)的摩擦力。在球籠式等速萬向節(jié)的運動過程中,各個鋼球隨著轉角δ的變化在星形套內溝道和鐘形殼外溝道內往復運動,并保持始終處在同一水平面上。鋼球運動時由于運動方向的改變,會導致鋼球所受到的摩擦力方向發(fā)生變化,即在運動的一個周期內,摩擦力的值將有正負的變化。鋼球在溝道內所受到的摩擦力為滑動摩擦力和滾動摩擦力,這兩者分別為

式中:Fh為鋼球在溝道內運動過程中所受到滑動摩擦力;Fg為鋼球在溝道內運動過程中所受到的滾動摩擦力;μh為鋼球在溝道內運動過程中所受到的滑動摩擦因數;μg為鋼球在溝道內運動過程中所受到的滾動摩擦因數,在存在潤滑的條件下,取 μh=0.05,μg=0.005;QNQ為鋼球在溝道內運動過程中所受到的法向接觸力;sign為特定函數符號,包含的值為鋼球在溝道內往復運動時正負的判別條件,即當sin x>0時,sign(sin x)=1,反之當 sin x<0時,sign(sin x)=-1。將 QNQ的表達式代入摩擦力 FNQ中,得

圖5和圖6分別為七溝道和六溝道球籠式等速萬向節(jié)鋼球在溝道內所受到的摩擦力FNQ與轉角δ和軸間擺角2θ的關系曲線。由圖可知:鋼球在溝道內所受到的摩擦力FNQ在星形套端輸入軸IN旋轉一周的過程中,隨著轉角δ的變化呈周期性變化,并在轉角為180°時發(fā)生方向的改變,從正值變?yōu)樨撝担驗殇撉虻倪\動方向發(fā)生了改變;當轉角 δ為0°,180°,360°時,鋼球處在最外端和最內端,其所受到的摩擦力絕對值最大;當轉角δ為90°,270°時,鋼球處在中間位置,其所受到的摩擦力絕對值最小;隨著軸間擺角2θ的增大而增大,擺角從0°到35°的過程中,鋼球所受到的摩擦力FNQ絕對值分別增加了近10 N,增長幅度約為17%;軸間擺角為0°時,摩擦力不變;軸間擺角為35°時,最大與最小法向摩擦力絕對值差值可達近20 N。七溝道球籠式等速萬向節(jié)所受到的摩擦力在任意的軸間擺角下均小于傳統(tǒng)的六溝道球籠式等速萬向節(jié),小載荷意味著同等材料和工況條件下能夠獲得更長的使用壽命[6-8]。
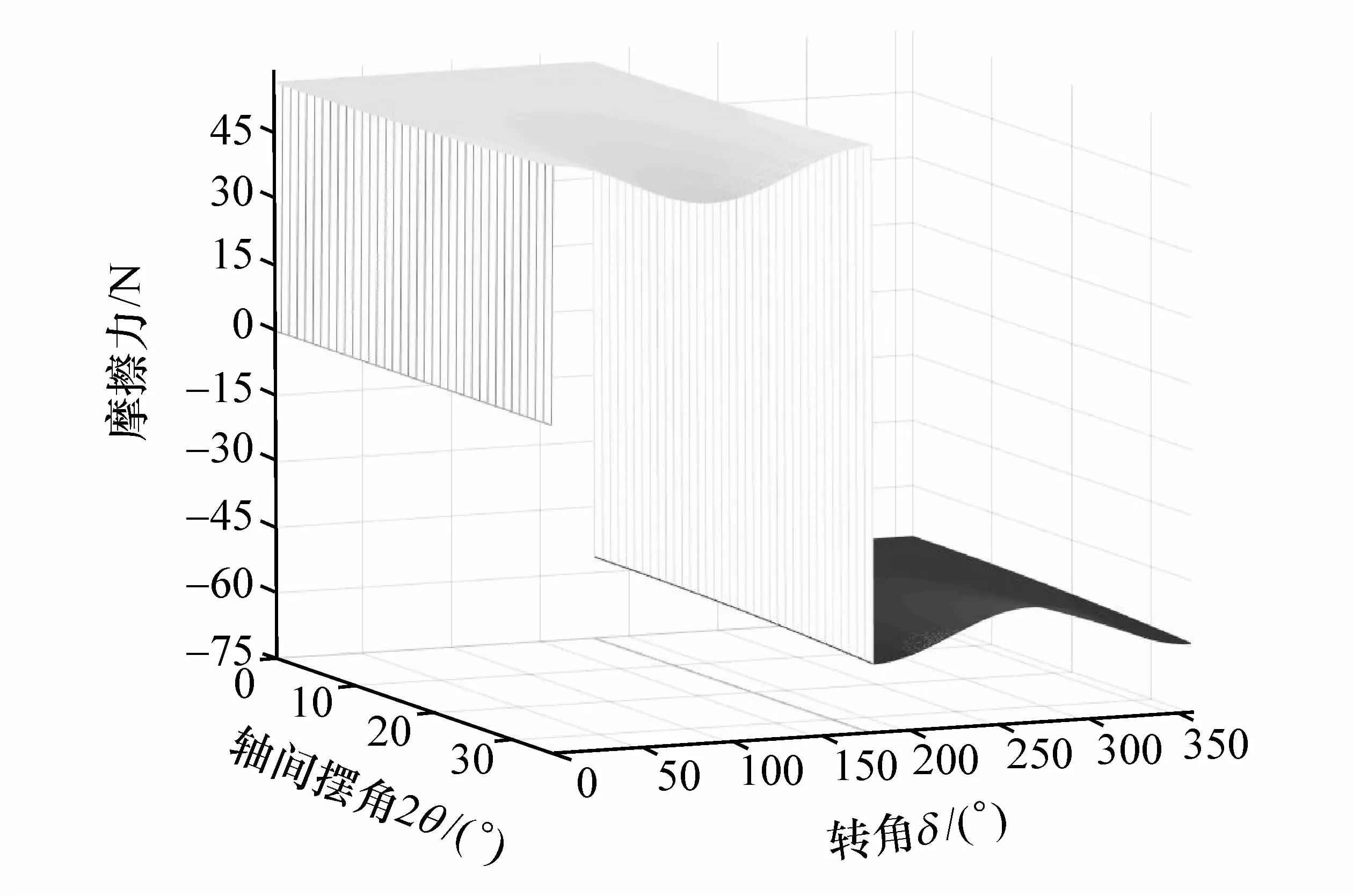
圖5 七溝道萬向節(jié)的變化規(guī)律

圖6 六溝道萬向節(jié)的變化規(guī)律
4 鋼球與保持架之間的摩擦力
由于保持架的窗口允許鋼球能夠在垂直于星形套輸入軸的平面方向上有移動,即在球籠式等速萬向節(jié)的運動過程中,由于軸間擺角2θ的不斷變化,鋼球也會在保持架窗口內運動。運動過程中,鋼球與保持架窗口上下表面接觸,其所受到的摩擦力包括滑動摩擦力和滾動摩擦力,可分別表示為

式中:F′h為鋼球在保持架窗口內運動過程中所受到滑動摩擦力;F′g為鋼球在保持架窗口內運動過程中所受到的滾動摩擦力;μ′h為鋼球在保持架窗口內運動過程中所受到的滑動摩擦力摩擦因數;μ′g為鋼球在保持架窗口內運動過程中所受到的滾動摩擦力摩擦因數,在存在潤滑的條件下,取 μ′h=0.05,μ′g=0.005;Q′JQ為鋼球在保持架窗口內運動過程中所受到的法向接觸力。將Q′JQ的表達式帶入摩擦力F′JQ中,得七溝道球籠式等速萬向節(jié):

六溝道球籠式等速萬向節(jié):

其中 φ=arccos(e cosθ/Rg)
圖7為鋼球與保持架窗口摩擦力隨軸間擺角2θ的變化規(guī)律。由圖可知,球籠式等速萬向節(jié)鋼球在保持架窗口內所受到的摩擦力FJQ隨著軸間擺角2θ的增大呈正比例函數增大,但在軸間擺角從0°到35°的變化范圍內,摩擦力FJQ的變化只有不到5 N,該摩擦力的大小與前面討論過的法向接觸力和摩擦力有著較大數量級差別,對于球籠式等速萬向節(jié)的運動影響極小,并不是影響使用壽命等的主要因素,但仍可發(fā)現(xiàn)七溝道球籠式等速萬向節(jié)所受到的摩擦力在任意軸間擺角下均小于六溝道的,亦可證明其結構的優(yōu)越性。

圖7 鋼球與保持架窗口摩擦力隨軸間擺角2θ的變化規(guī)律
5 球籠式等速萬向節(jié)的磨損分析
磨損率是兩零部件接觸發(fā)生摩擦過程中的一個重要基本量,本研究中分析的磨損率僅為在穩(wěn)定磨損期的磨損率,影響磨損率的因素除了材料本身的特性之外,也與作用在接觸表面的載荷有關。球籠式等速萬向節(jié)因鋼球與星形套內溝道和鐘形殼外溝道的法向接觸力關系,確定了其磨損類型為疲勞磨損。一直以來,廣泛應用的計算接觸物體疲勞磨損的磨損率主要應用的都是Archard磨損理論模型,其數學表達式為

式中:V為磨損量;K為磨損系數;P為兩接觸部件間的法向接觸力;H為接觸材料的硬度;L為兩接觸部件間相對移動的距離。
Archard磨損理論模型提出,摩擦副只有在接觸表面較高的微凸體上才有相應的接觸作用,上下微凸體接觸后,因為相對運動和載荷的作用而產生應力集中,從而發(fā)生塑性變形。圖8為Archard磨損理論模型。由圖可知,假設兩半球狀微凸體有接觸并發(fā)生相對運動,則有

式中:a為接觸表面半徑;A為接觸表面面積;FN為法向接觸力。在摩擦磨損過程中產生的一個磨損微粒體積為


圖8 Archard磨損理論模型
單位時間內相對移動的距離為

則體積磨損率為

則在整個相互接觸平面上有

其中單位時間內相對移動距離可以表示為

式中v1,v2分別為上下運動體(鋼球和星形套)接觸點的線速度。則體積磨損率可表示為

將前述中求得的轉速差(v1-v2)和法向接觸力QNQ代入上式,得

式中:n為鋼球數;φ=arccos(e cosθ/Rg)。
取K=1.1977×10-4,H=355 MPa,求得的體積磨損率V的單位是m3/s,與數學模型中等式右側的計算單位相同;由上式可以看出,體積磨損率V是星形套端輸入軸轉速ωN、轉角δ和軸間擺角2θ的函數。在球籠式等速萬向節(jié)運動過程中,轉角δ一直是個變量。圖9和圖10為七溝道和六溝道球籠式等速萬向節(jié)鋼球和星形套間體積磨損率V與轉角δ、軸間擺角2θ的關系曲線。由圖可知,在輸入軸轉速ωN不變的情況下,體積磨損率V隨著轉角δ在旋轉一周的過程中呈周期性變化,在0°,360°轉角位置時最大,此時鋼球運動到溝道的最外端位置;在90°和270°轉角位置時最小,此時鋼球運動到溝道的中間位置。體積磨損率V隨著軸間擺角2θ先變大再變小,最大單位時間內體積磨損率值約為 9.0×10-10mm3/s。

圖9 七溝道的體積磨損率V特性

圖10 六溝道的體積磨損率V特性
圖11 為軸間擺角為35°時體積磨損率隨著鋼球與最外端的距離的變化規(guī)律。由圖可知,體積磨損率V隨著軸間擺角2θ先變大再變小,最大單位時間內體積磨損率值分別約為 9.0×10-10和 10.0×10-10mm3/s。

圖11 瞬時磨損率V隨鋼球與最外端的距離的變化規(guī)律
由于磨損是一個持續(xù)的過程,單位時間內體積磨損率越小,能夠獲得更長的使用壽命,圖12為體積磨損率V隨轉角δ和輸入軸轉速ωN的變化規(guī)律。由圖可知,在軸間擺角2θ不變的情況下,單位時間內體積磨損率V隨著轉角δ在旋轉一周的過程中呈周期性變化。在0°,360°轉角位置時最大,此時鋼球運動到溝道的最外端位置;在90°和270°轉角位置時最小,此時鋼球運動到溝道的中間位置。隨著星形套端輸入軸轉速ωN的增長而線性增長,最大轉速時的最大體積磨損率值分別約為9.0×10-10和10.0×10-10mm3/s,六溝道球籠式等速萬向節(jié)的最大單位時間內體積磨損率要略大于革新的七溝道球籠式等速萬向節(jié)。

圖12 體積磨損率V隨轉角δ和輸入軸轉速ωN的變化規(guī)律
6 仿真分析
本文中采用SolidWorks完成了七溝道球籠式等速萬向節(jié)的幾何模型構建以及裝配。根據七溝道球籠式等速萬向節(jié)結構參數,完成了幾何模型的構建,利用幾何模型完成后續(xù)的動力學建模及仿真過程。將球籠式等速萬向節(jié)分別調整裝配至軸間擺角為0°(零擺角工況)和 35°(最大擺角工況),將 360°/s2的角加速度和125 N·m的轉矩施加在星形套與大地所構成的旋轉副約束上,同時為保證受力平衡,需要在鐘形殼輸出軸端設置與輸入端等大反向轉矩,并按照仿真時間1 s、步長0.001進行仿真[9-10]。
(1)摩擦力測試
與星形套對鋼球法向力的仿真值相同,圖13和圖14為七溝道球籠式等速萬向節(jié)在軸間擺角為0°和35°情況下,鋼球與星形套摩擦力隨轉角的變化情況。旋轉一周過程中,星形套對鋼球的法向力仿真值也需要借助Matlab的二次計算而得出。由圖13和圖14可知,仿真值與理論值的變化規(guī)律高度吻合,由于動靜摩擦轉換系數值的選取、接觸變形導致的從點接觸變?yōu)樾E圓面接觸等因素導致仿真值略大于理論值,但誤差不足10%,處在可以接受的允許誤差范圍內。

圖13 軸間擺角為0°時摩擦力
(2)瞬時磨損率測試
與星形套對鋼球法向力、摩擦力的仿真值相同,圖15和圖16為球籠式等速萬向節(jié)在軸間擺角為0°和35°情況下,旋轉一周過程中星形套與鋼球間的瞬時磨損率隨轉角的變化情況。由圖可知,仿真值與理論值的變化規(guī)律基本一致,數量級保持一致,兩者微小偏差在可以接受的范圍內。通過對軸間擺角為0°和35°時,七溝道球籠式等速萬向節(jié)星形套對鋼球的周向力、法向力、摩擦力和磨損率仿真值和理論值的仿真可以發(fā)現(xiàn),球籠式等速萬向節(jié)的運動學與動力學的仿真試驗可信度較高,可作為今后研究疲勞等工作的基礎和依據。

圖14 軸間擺角為35°時摩擦力

圖15 軸間擺角為0°時磨損率

圖16 軸間擺角為35°時磨損率
7 結論
(1)鋼球在溝道內既滑又滾的運動模式,摩擦力包含滑動摩擦力和滾動摩擦力,并且在鋼球運動過程中隨著鋼球運動方向的改變,摩擦力的方向也會隨之而變,摩擦力的正負會有所改變;
(2)鋼球在溝道內受到的摩擦力是轉角δ和軸間擺角2θ的函數,在轉角δ一定時,摩擦力隨著軸間擺角的增大而增大,摩擦力隨著轉角δ的變化呈周期性變化;
(3)保持架窗口對鋼球的摩擦力隨著軸間擺角的增大而增大,但該摩擦力本身的值和變化范圍都非常小;
(4)球籠式等速萬向節(jié)的磨損類型為疲勞磨損,體積磨損率V隨著轉角δ周期性變化,隨軸間擺角的先變大再減小;
(5)七溝道等速萬向節(jié)比六溝道內的摩擦力均小,同樣的使用工況條件下,可以獲得更長的使用壽命。

