或然與必然思想

高慧明

北京市中學數學特級教師，現任教于北京市第十二中學;教育部課程改革“全國先進工作者”，教育部“國培計劃”全國中小學教師培訓、班主任培訓、校長培訓特邀主講專家，受邀為教育部“國培計劃”做有關數學課堂教學、班級管理、教師專業成長等專題報告多場;在《教育研究》《中國教育學刊》《數學教育學報》《數學通報》等學術期刊上發表論文500余篇，其中100余篇被中國人民大學復印報刊資料《中學數學教與學》《中小學教育》全文轉載;已出版個人專著《高中數學思想方法及應用》《高考數學命題規律與教學策略》《讓高中生學會學習》《高慧明數學教學實踐與研究》（叢書）等多部，應邀主編、參編教材和教學著作30余部。

世間萬物千姿百態、千變萬化，人們對世界的了解、對事物的認識是從不同側面進行的，人們發現的事物或現象可以是確定的，也可以是模糊的、隨機的。

概率研究的就是隨機現象，研究的過程是在“偶然”中尋找“必然”，然后用“必然”的規律去解決“偶然”的問題。這其中所體現的數學思想就是或然與必然的思想，也稱統計與概率的思想。

隨機事件發生可能性的大小是概率研究的主要內容，而通過試驗來觀察隨機事件發生可能性的大小是研究的常用方法。在相同的條件下，重復進行[n]次試驗，某一事件A出現的次數[m]是頻數，也就是事件A出現的頻數。如果試驗的次數不斷增加，事件A發生的頻數穩定在某個數上，我們就把這個常數記作P（A），稱為事件A的概率。

事件的概率是確定的、不變的常數，是理論上的精確值，而頻率是某次具體試驗的結果，是不確定的、變化的數，盡管這種變化的可能性非常小。這里的概率是用頻率來界定的，在等可能性隨機試驗中，雖然頻率總是在很小的范圍內變化，但我們可以認為頻率和概率的相關性非常強。也就是說，在一次試驗中，事件A出現的頻率越大，事件A的概率就越大;事件A出現的頻率越小，事件A的概率就越小。反之亦然。

生活中的很多現象都是隨機現象，如氣候變化、物價變化、體育比賽、汽車流量、彩票中獎等。這些隨機事件，如果能夠比較準確地預測其發生可能性的大小，就會為我們的工作和生活帶來很多方便。事實上，隨著科技的發展，人們已經能夠對一些隨機現象做出比較準確的預測，如氣象部門已經能夠比較準確地預報天氣變化。預測離不開對數據的分析和對事件發生可能性大小的定量刻畫，這正是統計與概率（或然與必然思想）研究的主要內容。

或然與必然思想主要應用于統計與概率領域。以小學數學教學為例，小學數學第一、第二學段都安排了可能性的內容，如會求簡單的等可能性隨機事件發生的可能性、根據等可能性事件設計公平的游戲規則等。統計推斷中，人們往往通過分析隨機事件的相關數據，對隨機事件發生的可能性進行預測。如2010年南非世界杯西班牙對荷蘭的決賽，有人預測西班牙奪冠，理由是西班牙是近年的歐洲冠軍，實力雄厚;還有人預測荷蘭衛冕，理由是荷蘭曾兩次獲得世界杯亞軍。用或然與必然的思想來分析，歷史上，西班牙隊和荷蘭隊一共交手9次，其中荷蘭4勝1平4負，與西班牙隊實力不分上下，所以兩隊奪冠的可能性各占一半。

中學數學中，概率的相關內容也放在了重要位置，如等可能事件的概率、互斥事件發生的概率、相互獨立事件同時發生的概率、[n]次獨立重復試驗發生了[k]次的概率，以及隨機事件的分布列與數學期望等重點內容。教學這些內容時，教師在加強基本概念和基本方法教學的同時，更應注重運用或然與必然的思想。

教學涉及或然與必然思想的相關內容時，應注意以下幾點。

第一，隨機事件的發生是有條件的。在一定條件下，事件發生的可能性有大有小，條件變了，事件發生的可能性大小也可能會變化。例如，種子的發芽率與很多因素有關，如種子的質量、保存期限、溫度、水分、土壤、陽光、空氣等。在各種條件都合適的情況下，發芽率可能高達90%;條件不合適，發芽率可能降到50%，甚至不發芽。

第二，不能混淆“頻率”與“概率”。如用擲硬幣試驗去驗證概率，從概率的統計定義而言，做拋硬幣試驗是可以的，因為它可以使學生參與實踐活動，經歷知識的形成過程，提高學習興趣。不過，教師心中要明白：試驗次數少的時候，頻率與概率的誤差可能會比較大，可是試驗次數多，也不能每次都保證頻率與概率相差很小，或者說試驗次數足夠多的兩次試驗，也不能保證試驗次數多的比試驗次數少的誤差小。這是隨機事件本身的特點決定的，教師要通過通俗的語言使學生清楚這一點，使學生理解概率的統計定義。

第三，創設聯系學生生活的情境時，要注意每個基本事件是否具有等可能性。下面的問題就不合適：全班50個學生，選一人代表全班參加科普知識競賽，張三被選中的可能性是多少？事實上，參加競賽是有一定條件的，如需要學習好、知識面寬等，每個學生被選中的可能性是不相等的。

第四，概率是理論上的精確值，但是隨機事件在某次試驗中可能出現意外，即頻率與概率會有一定的偏差。隨機中有精確，精確中有隨機，這是對待概率的一種科學態度。如：連續兩次擲一枚硬幣，若第一次正面朝上，那么第二次一定是反面朝上嗎？從概率的角度分析，每拋一次，硬幣正面朝上和反面朝上的可能性都是二分之一，并不會因為第一次正面朝上而影響第二次正面朝上。因此，第二次正面朝上和反面朝上的可能性仍然相等。再如：天氣預報預測明天降雨的概率是90%，明天一定會下雨嗎？明天是否降雨是一個隨機事件，盡管降雨概率高達90%，但可能性大的事件也可能不發生，所以不能說明天一定會下雨。

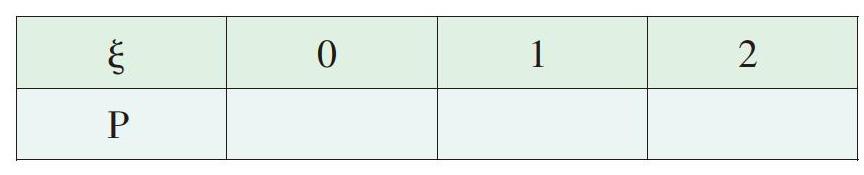
還看一個例子：從裝有3個紅球、2個白球的袋中隨機取出2個球，設其中有ξ個紅球，則隨機變量ξ的概率分布為：

本題是求隨機變量分布列的問題，其中所求概率又是等可能事件的概率問題，所以有：

我們研究離散隨機變量時，不僅要關心某一次隨機試驗中到底取什么值的問題，還要關心隨機變量在取某一個值或某一批值時可能性的大小。只有如此，我們才能確切地掌握隨機變量的取值規律，解決相應的問題。這就使我們對“或然”與“必然”的研究又深入了一步，即從“分布”與“期望”兩個方面獲取隨機變量的規律，在“或然”中尋找“必然”。

責任編輯? 姜楚華