圓周分段式密封動壓浮起力數值仿真計算

李小芬，周 芮，涂 霆

(1.北京航天動力研究所，北京 100076； 2.西安航天動力研究所，陜西 西安 710100)

0 引言

氫氧火箭發動機氧渦輪泵動密封系統對渦輪泵設計來說至關重要，尤其是氧渦輪泵中防止液氧介質和驅動渦輪的富氫燃氣相混合的氦密封[1]。氧渦輪泵氦密封是防止液氧與燃氣混合的唯一屏障，是渦輪泵的關鍵部件[2]。以往的型號上多采用浮動環或者端面密封，而圓周分段式密封因其結構緊湊，適應高轉速，泄漏量低，且具有軸向、徑向補償能力，為國外主要型號氧渦輪泵研制所青睞。

圓周分段式密封設計的關鍵在于計算動壓槽所產生的動壓浮起力。目前由連續性方程所推導出的一維公式最為簡單快捷[3]；也有忽略間隙高度，通過數值分析方法求解等溫條件下的二維雷諾方程來計算浮起力的方法[4-5]。但這兩種方法的簡化程度較高，而利用CFD三維仿真的計算方法更貼近實際流動，可以準確直觀地反映密封的流動特性，同時更便于考慮由加工誤差造成的密封流體膜變形對浮起力的影響。

本文利用Fluent流體分析軟件來分析圓周分段式密封流場內的流動，以便得到動壓槽所產生的浮起力，并綜合一維計算方法和國外文獻中計算結果進行比較，驗證三維仿真計算方法的準確性；分析氣膜厚度，動壓槽深度，槽數以及加工誤差導致的軸偏斜和槽偏斜等因素對浮起力的影響。

1 圓周分段密封結構和工作原理

1.1 密封原理

典型的圓周分段式氦密封的組件包括分段密封環、密封殼體、蓋板和彈簧等，如圖1所示。兩組結構對稱的分段密封環背對背放置，兩環之間由彈簧預緊，貼合于密封殼體和蓋板上，腔內供隔離氦氣。密封環由分段的扇形密封環構成[6-7]，由外表面上的箍簧約束，裝配狀態下抱緊軸套，其內表面與轉子外表面構成主密封面，貼合于密封殼體的端面為副密封面。

每段密封環的主密封面上都設有軸向輸入槽與平衡環形槽，氦氣由輸入槽流入環形槽，受密封壩節流作用，減壓泄出。內表面的軸向輸入槽之間設置瑞利動壓槽，如圖2所示。瑞利動壓槽為周向槽，從軸向輸入槽開始，沿周向在兩個軸向輸入槽之間的密封面上占一定的角度，與密封內徑面之間形成臺階。轉軸工作時帶動軸向輸入槽中的介質沿周向進入動壓槽，經槽根部臺階的節流，形成高壓區，從而產生動壓力推開密封環，使密封環處于極小間隙的浮動狀態。密封內表面上的這種布置，既利用氣體靜力平衡原理提高了內表面壓力，使其在徑向壓力分布上得到極大的平衡，又利用動壓槽所產生的動壓力，進一步克服密封環的殘余外載荷，使軸和密封環維持一個微小間隙的流體膜潤滑狀態。

圖1 圓周分段氦密封結構Fig.1 Schematic of circumferential segmented seal

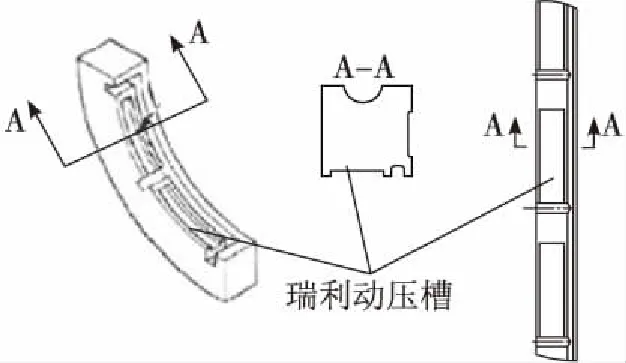
圖2 瑞利動壓槽結構Fig.2 Schematic of rayleigh steps

這種帶動壓槽的圓周分段氦密封結構在關機階段在箍簧的壓力下抱住軸，所以在渦輪泵預冷階段氦氣消耗量很低；工作階段通過軸的旋轉獲得動壓浮起力，使軸和密封環分離，從而可以在保持氦氣泄漏量很低的同時防止密封環的摩擦磨損。

1.2 受力分析

圓周分段式密封環中每一個分段環都完全相同，分段環中每一個動壓槽也是完全一致的，因此密封環的受力沿周向呈周期性分布。忽略搭接處的受力，選取其中單槽截面的簡化受力分布如圖3所示。上游壓力作用于密封環外徑的閉合力和箍簧的約束力以及副密封端面的摩擦力(以密封環呈浮起的運動趨勢為例)共同形成徑向閉合力。密封間隙內氣體所產生的總浮起力由靜浮起力、密封壩區域內氣體所產生的打開力和動壓槽所產生的動壓浮起力組成。

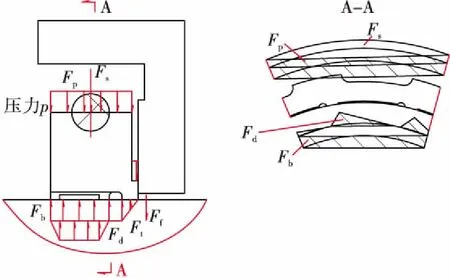
圖3 密封受力分析Fig.3 Pressure profile of segmented rayleigh step seal

為了使密封環處于較極小間隙的浮動狀態，動壓槽所產生的動壓浮起力須和徑向不平衡力相等，即

Fd=(Fp-Fb-Ft)+Fs+Ff

(1)

式中：Fd為瑞利動壓槽產生的動壓浮起力；Fb為輸入槽和環形槽內氣體的靜壓力；Ft為密封壩區域內氣體所產生的打開力；Fp為密封外載荷在外徑產生的閉合力；Fs為箍簧產生的閉合力；Ff為副密封面產生的摩擦力。

為了簡化計算動壓槽所產生的浮起力，假設壓力在槽內軸向及膜厚方向都不變，如圖4所示。流過軸向環形區域的流動為Couette剪切流[8]。

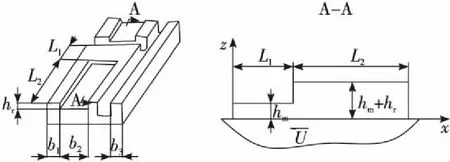
圖4 一維計算模型Fig.4 One-dimentional calculation model

由連續性方程可得進出口質量流量相等，從而計算出峰值壓力

(2)

式中U為軸的周向速度。

假設壓力在密封間隙內呈線性變化，因此由峰值壓力可以得到浮起力

(3)

2 密封環動壓浮起力的三維數值仿真計算

2.1 模型及其參數

本文選用文獻[3]中LE-7作為計算模型(見表1和表2)，計算其在不同膜厚和不同動壓槽深度下浮起力的變化，并與文獻[3]中的結果進行對比分析；之后在此基礎上改變動壓槽數量，考慮軸偏斜和動壓槽加工偏斜等因素對浮起力的影響。

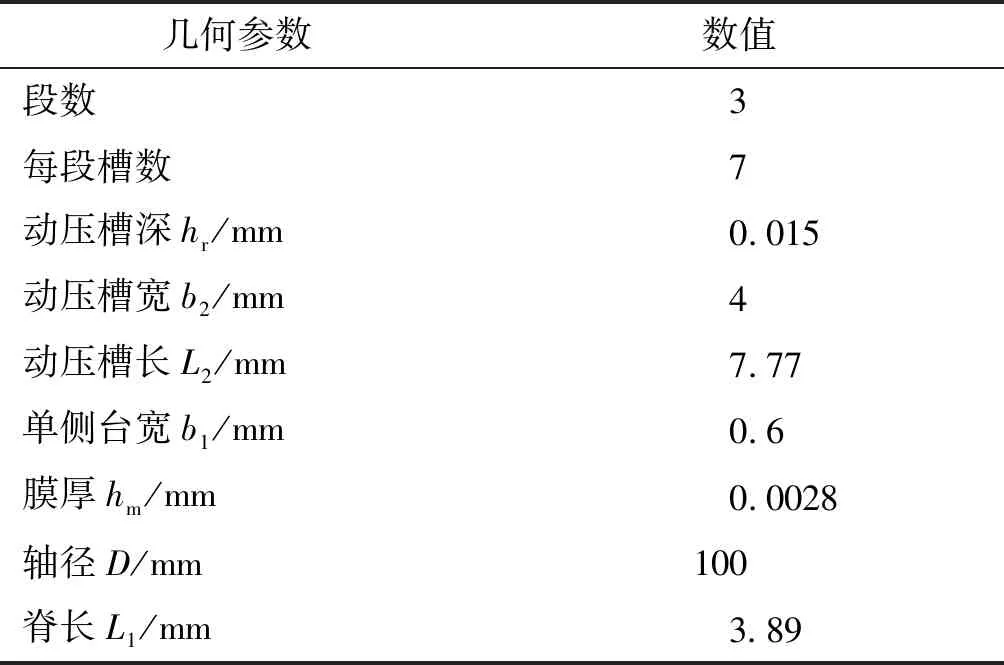
表1 LE-7模型幾何參數

表2 LE-7模型工況參數

2.2 模型結構和邊界條件

參考國外計算浮起力的方法，選取一個周期的動壓槽、支撐瓦面和軸向輸入槽為分析對象[2-3]，如圖5所示。動環表面為旋轉壁面，靜環內徑表面為靜止壁面，瑞利動壓槽開在靜環內徑面，軸向兩側一側作為壓力入口，另一側為壓力出口，氣膜周向兩側為周期邊界。

2.3 基本假設

為了簡化計算，對密封間隙內流場做出以下假設：

1)忽略體積力的作用，如重力或磁力；

2)密封間隙內為等溫環境，因此不考慮密封氣體的黏度和密度隨溫度的變化；

3)密封氣體滿足理想氣體狀態方程；

4)流動為層流[9]，不存在渦流和湍流；

5)流體在固體界面無滑移。

2.4 網格劃分

利用Gambit軟件對一個周期的密封氣膜進行網格劃分，網格劃分方式主要包括以下幾個要點：

1)網格劃分采用正交性好的六面體結構。

2)相比于軸向和周向尺寸，膜厚方向的尺寸小了幾個數量級，為了盡量減小網格的長短邊比值，同時兼顧膜厚和動壓槽深的微小尺寸，將模型劃分為動壓槽，脊以及軸向槽3個部分分別劃分網格。膜厚劃分5層網格，槽深劃分30層網格。

3)網格總數在90萬以上時浮起力和峰值壓力的變化不大，因此本文模型網格總數選擇在約90萬個。

2.5 求解器設置

采用基于壓力的求解器隱式求解，選擇層流模型壓力速度耦合采用SIMPLEC算法，在較細網格劃分下，方程二階離散余量對計算結果影響不顯著，壓力和動量的離散分別采用標準和一階迎風格式。

3 計算及結果分析

3.1 三維仿真與一維計算結果對比分析

圓周分段密封單個周期間隙內的三維壓力場分布如圖6所示，左側為模型對稱中心面上壓力變化，氣體流入瑞利動壓槽根部后壓力激增，這是由于氣體進入槽后，在根部受到阻擋不斷壓縮形成高壓。

而一維計算中忽略了密封間隙內氣膜寬度方向和厚度方向的壓力變化，假設壓力沿周向為線性變化，如圖6(a)所示。對于設計階段，一維公式簡單快捷，但在實際流動中，氣體經轉軸的帶動流入瑞利動壓槽，在槽根部受到阻擋，氣體不斷壓縮，壓力激增，壓力變化并非簡單的線性變化。

分別用Fluent和一維計算方法分析LE-7模型在膜厚為1.7 μm，2.8 μm和3.9 μm時，浮起力隨瑞利動壓槽深的變化，并和文獻[3]中經過實驗驗證的浮起力結果相比較，如圖7所示。

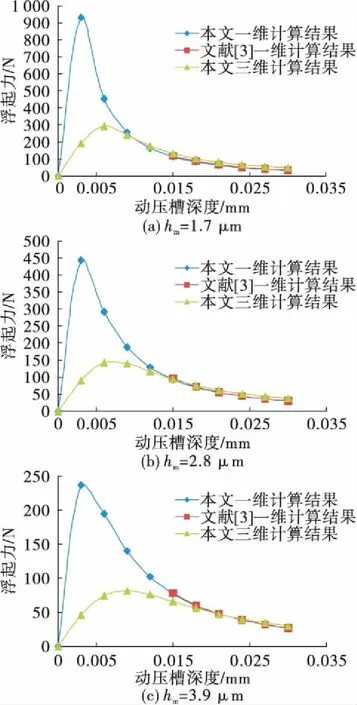
圖7 LE-7不同槽深和氣膜厚度對浮起力的影響Fig.7 Effect of film thickness and step depth on opening force for LE-7

由圖7可以看出，浮起力隨膜厚的增加而減小。而當動壓槽深度大于0.015 mm時，三維仿真計算和一維計算結果相差很小，都是隨著槽深的減小浮起力增大，并且和文獻[3]中的數據相差小于3%。當動壓槽深小于0.015 mm時，三維仿真和一維計算出現較大差異，主要原因是一維計算中忽略了氣膜寬度方向的壓力變化，動壓槽深度越小，寬度上的密封壓力變化影響越大。一維計算中隨著槽深的減小浮起力不斷增大，直到槽深減小至約0.003 mm時浮起力才達到最大值；而三維仿真中動壓槽深約0.008～0.01 mm時，動壓浮起力達到最大值，當動壓槽深小于0.008～0.01 mm時，槽深越小，浮起力也越小，分析原因是當動壓槽深太小或太大，都會削弱氣體在高速下壓縮產生的動壓效應，因此，動壓槽深度存在最優值，這和文獻[10]中提到的結論一致。

3.2 膜厚和瑞利動壓槽深度對浮起力的影響

在每段槽數為5槽下，不同槽深和膜厚對浮起力的影響如圖8所示。密封氣膜厚度越小，浮起力就越大。因此如果密封環在工作時密封間隙減小，浮起力就會增大，從而密封環克服閉合力浮起，密封間隙也會隨之增大，而間隙增大時浮起力減小，又會使密封間隙趨于減小，最終浮起力和閉合力會保持平衡，密封間隙可以維持在微米級。

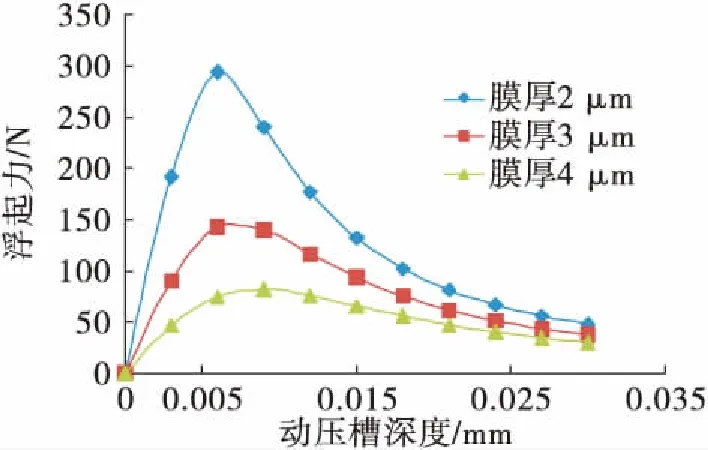
圖8 不同槽深和膜厚對浮起力的影響Fig.8 Effect of film thickness and step depth on opening force

對于動壓槽深度的影響，浮起力的變化并非為簡單的單調函數。隨著動壓槽深不斷增大，動壓槽深浮起力先增大后降低，因此動壓槽深存在最優值。不同膜厚下的動壓槽深最優值存在差異，膜厚越大，動壓槽深最優值越大，在膜厚為2～4 μm時，動壓槽深最優值為0.008～0.01 mm。實際工作中密封環可能會發生磨損，槽深變小，浮起力增大，從而平衡間隙變大，防止進一步磨損；但槽深小于0.008 mm左右時浮起力將會減小，這樣會導致磨損加劇，影響密封性能，因此在動壓槽的設計過程中，槽深不宜過小。

3.3 槽數對浮起力的影響

在膜厚為3 μm時，槽數對浮起力的影響如圖9所示。整體來看浮起力隨動壓槽深度變化趨勢相同，槽數越多，浮起力峰值點對應的動壓槽深度越大。一般動壓槽深度的設計值為0.02～0.04 mm，允許少量磨損，可見在這個范圍內，總槽數越少，浮起力越大。但是槽數越多，整環的浮起力分布越均勻，因此槽數一般在滿足浮起力要求下取最大值。

圖9 不同槽數對浮起力的影響Fig.9 Effect of step number on opening force

3.4 工作時軸偏斜對浮起力的影響

在密封環的實際工作中，軸套外圓的加工誤差可能導致轉軸外徑和密封環內徑產生一定角度，考慮軸偏移對浮起力的影響，將密封氣膜簡化為楔形間隙模型(如圖10所示)進行三維仿真計算，分別得到單段槽數為3槽、5槽和7槽的密封環隨軸偏斜角度的浮起力變化，如圖11所示。由圖11可見，軸偏斜角度越大，浮起力越小，并且都小于無偏斜時的浮起力；同時槽數越少，浮起力下降越快。因此應盡量避免軸偏斜的情況發生。

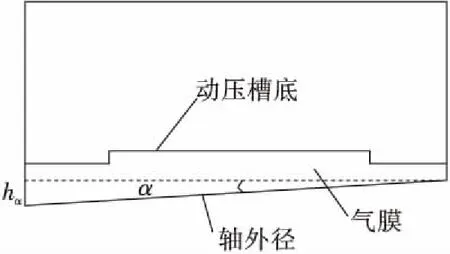
圖10 軸偏斜示意圖Fig.10 Schematic of shaft distortion

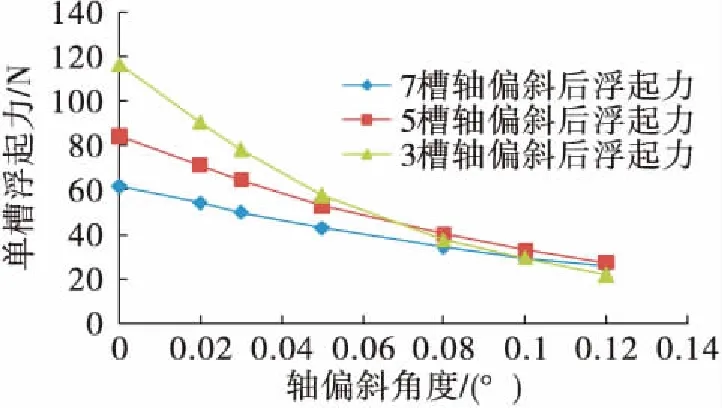
圖11 軸偏斜對浮起力的影響Fig.11 Effect of shaft distortion on opening force

3.5 瑞利動壓槽加工偏斜對浮起力的影響

在密封環的實際工作中，轉軸可能會和密封環內徑存在一定角度，考慮軸偏移對浮起力的影響，將密封氣膜簡化為楔形間隙模型(圖12)進行三維仿真計算，軸偏斜角度所對應厚度如表3所示。分別得到單段槽數為3槽、5槽和7槽的密封環隨軸偏斜角度的浮起力變化，如圖13所示。由圖13可見，軸偏斜角度越大，浮起力越小，并且都小于無偏斜時的浮起力；同時槽數越少，浮起力下降越快。因此工作時應盡量保證副密封面的平面度，避免軸偏斜的情況發生。

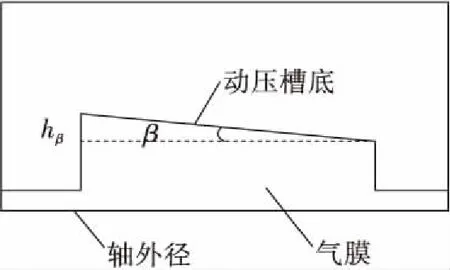
圖12 槽偏斜示意圖Fig.12 Schematic of Rayleigh step distortion

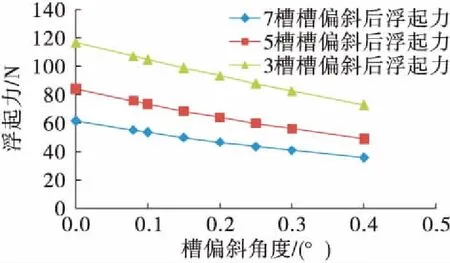
圖13 槽偏斜對浮起力的影響Fig.13 Effect of Rayleigh step distortion on opening force

4 結論

本文針對氫氧發動機氧渦輪泵中的圓周分段密封進行了數值仿真，獲得了動壓槽所產生的動壓浮起力，并得到以下結論：

1)對于圓周分段式密封動壓浮起力的計算，三維仿真和一維計算方法在動壓槽深度大于0.015 mm左右時結果基本一致，并與文獻中結果相差小于3%；當槽深小于0.015 mm時，三維仿真與一維計算結果相差較大，因此當槽深小于0.015 mm時，不適合采用一維計算。

2)當動壓槽深約為0.01 mm時，浮起力達到最大值。當槽深大于0.01mm時，浮起力隨槽深的減小而增大；當槽深小于0.01 mm時，浮起力隨槽深的減小而減小。而密封浮起力隨氣膜厚度的增大而減小。在實際工作中，密封環可能會發生磨損，槽深變小，浮起力增大，從而平衡間隙變大，防止進一步磨損；但槽深小于0.01mm左右時浮起力會減小，這樣會加重磨損，影響密封性能，因此在設計時動壓槽深度不能太小。

3)槽數越少，浮起力峰值對應的槽深越大；在大于峰值點的范圍內，槽數越少，浮起力越大。

4)軸偏斜角度越大，浮起力越小，且槽數越少浮起力減小得越快。

5)動壓槽底偏斜角度越大，浮起力越小。