三相逆變器雙閉環(huán)控制系統(tǒng)仿真研究

胡維飛，張永明

（上海電機學院電氣學院，上海201306）

0 引言

三相逆變器作為目前極其常見的電子設(shè)備，針對其輸出端的要求也越來越高，例如當負載頻繁變化時表現(xiàn)出較硬的輸出外特性、魯棒性好[1]。目前，對三相逆變系統(tǒng)控制器的研究，主流方法是采用比例積分[2-3]或者PR 控制[4]、重復控制[5]或者無差拍控制[6]等。對于直流輸入信號，其中PI 可以做到無靜差跟蹤，且具有控制結(jié)構(gòu)簡單、動態(tài)響應(yīng)較快以及魯棒性好等特點，在電氣工程領(lǐng)域得到廣泛應(yīng)用。比例諧振（PR）可以對某一特定頻率的正弦交流信號進行跟蹤。但是PR 控制在計算時需要進行離散化處理，并且PR 動態(tài)響應(yīng)速度不如PI 控制。重復控制雖然可以消除幅值和相位的穩(wěn)態(tài)誤差，但是，利用該方法時輸出周期有延遲且動態(tài)響應(yīng)不佳，并且控制器的設(shè)計比較復雜。無差拍控制雖然有著良好的動態(tài)響應(yīng)，且無超調(diào)現(xiàn)象，但是其控制特性在系統(tǒng)參數(shù)變化時有較大的影響，魯棒性較差，不利于對輸出電壓的控制[7]。

因此，本文將采用比例積分控制方案，利用電壓外環(huán)電流內(nèi)環(huán)的雙閉環(huán)控制策略作為三相逆變器的控制系統(tǒng)。本文通過詳細介紹三相逆變器的數(shù)學模型，計算雙閉環(huán)控制策略的傳遞函數(shù)，最后在MATLAB/Simulink 上搭建逆變系統(tǒng)的仿真模型，驗證控制策略的有效性。

1 三相逆變器的數(shù)學模型

1.1 基于三相靜止坐標系的數(shù)學模型

如圖1 所示為三相逆變器的主電路拓撲結(jié)構(gòu)，輸出端采用LC 濾波電路，其中，其中r 為濾波器的等效阻抗。直流側(cè)輸入電壓為udc，A、B、C 三點電壓分別為UA、UB、UC，他們是相對直流輸入端中點P 的三相電壓，輸出端電感電流分別為ila、ilb、ilc，電容電壓分別為Uoa、Uob、Uoc，流入三相負載的電流分別為ioa、iob、ioc[8]。

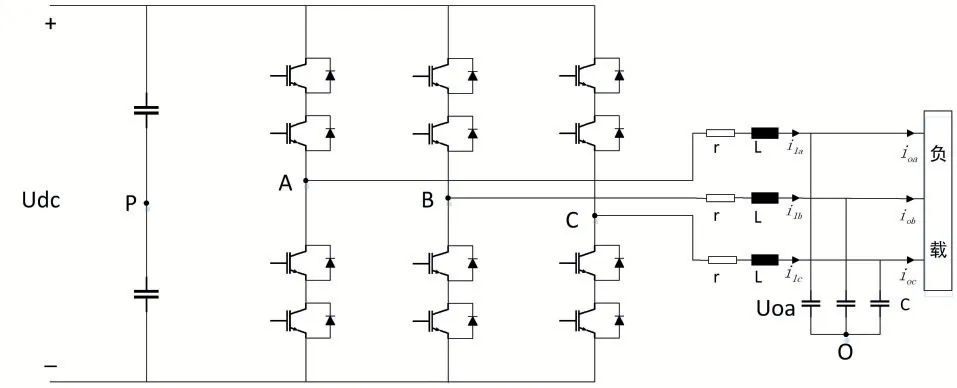
圖1 三相逆變器主電路拓撲圖

由KCL 和KVL 可列出下列方程：

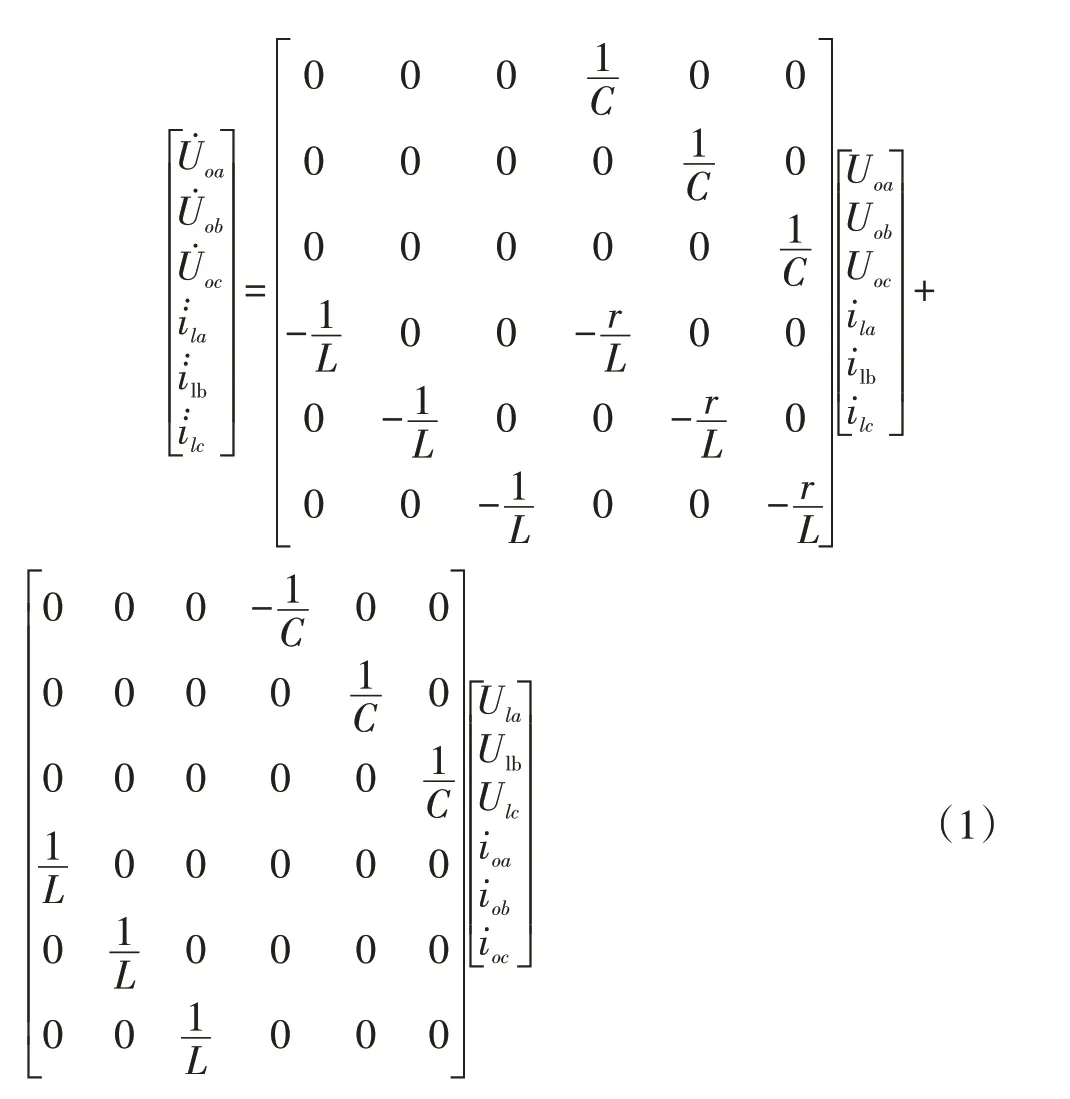
將上式化簡可得：

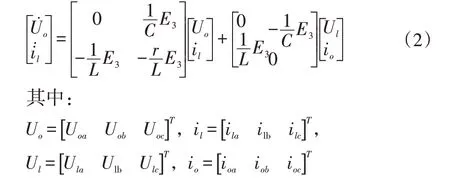
采用電容電壓和電感電流作為狀態(tài)變量，可得通用連續(xù)狀態(tài)空間模型為：

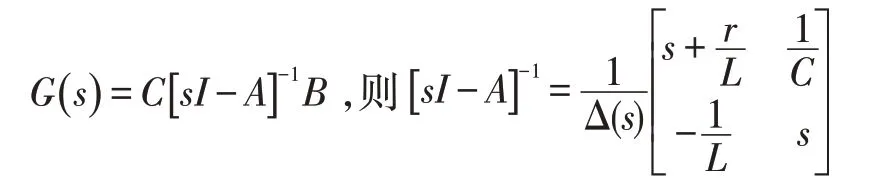
其中Δ(s)=s2+，由此可以求出輸入電壓同輸出電壓之間的傳遞函數(shù)為：

輸入電壓同輸出電流之間的傳遞函數(shù)為：

1.2 基于d-q旋轉(zhuǎn)坐標系下的數(shù)學模型

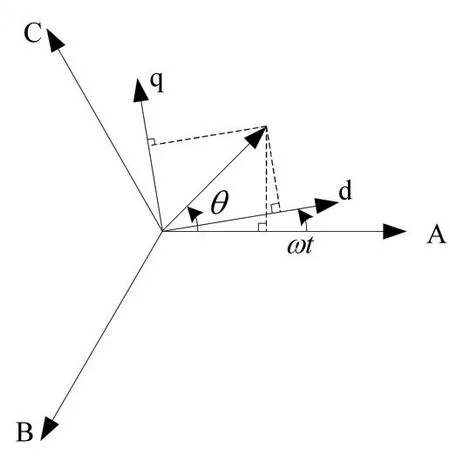
圖2 坐標變換圖

根據(jù)圖2 中各矢量的幾何關(guān)系，可以求出坐標變換后的狀態(tài)空間表達式如下：

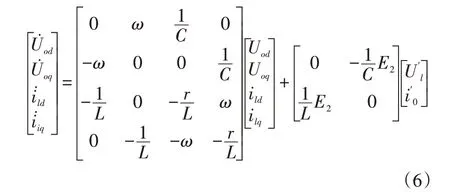
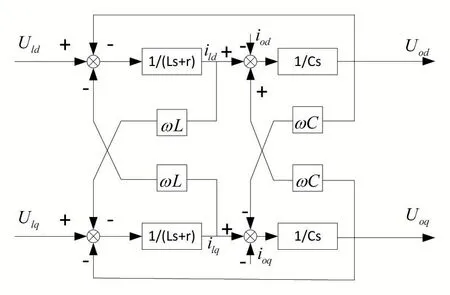
圖3 旋轉(zhuǎn)坐標系下逆變器數(shù)學模型

2 三相逆變器雙環(huán)控制策略分析

對于三相逆變器控制系統(tǒng)的雙閉環(huán)控制策略，電流內(nèi)環(huán)控制可以增加控制系統(tǒng)的帶寬，同時系統(tǒng)的瞬態(tài)響應(yīng)速度更快，當系統(tǒng)帶非線性負載時，適應(yīng)能力更強，且輸出電壓的諧波失真情況也隨之降低，提高系統(tǒng)輸出波形的穩(wěn)定性和供電質(zhì)量。而電壓外環(huán)控制的作用是使系統(tǒng)輸出波形能夠瞬時跟蹤給定值。目前，基于大多數(shù)逆變系統(tǒng)中常用的雙閉環(huán)控制的電流內(nèi)環(huán)控制策略是以輸出端的濾波電感電流為內(nèi)環(huán)控制或者以濾波電容電流為內(nèi)環(huán)進行控制。其中，采用濾波電容電流作為內(nèi)環(huán)進行控制時，由于電容電流能夠被瞬時控制，使得輸出電壓因為電容電流的微分環(huán)節(jié)得到矯正，因此，該系統(tǒng)的帶負載能力更強，本文將采用電容電流為內(nèi)環(huán)進行分析，如圖4 所示為電容電流為內(nèi)環(huán)的控制框圖。

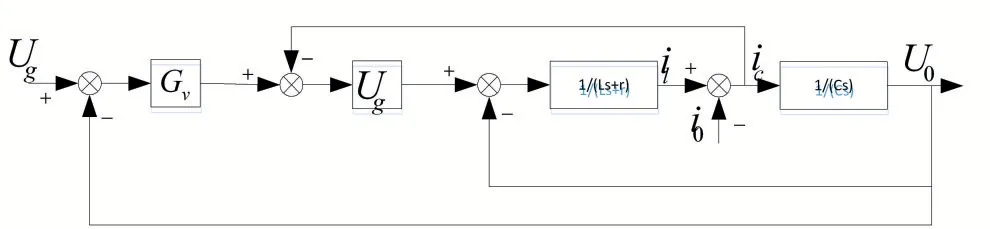
圖4 電容電流內(nèi)環(huán)電壓外環(huán)控制框圖

根據(jù)自動控制理論，可以采用極點配置法計算PI控制器的比例和積分控制參數(shù)，因為采用極點配置法時，比例和積分控制參數(shù)與閉環(huán)控制系統(tǒng)性能指標能建立量化關(guān)系，使得參數(shù)計算更加準確。圖4 中控制器的Gv與Gi分別定義為：

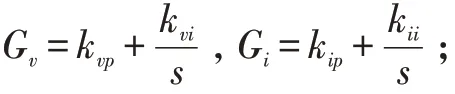
由圖4 可以推出逆變器的閉環(huán)系統(tǒng)特征方程：

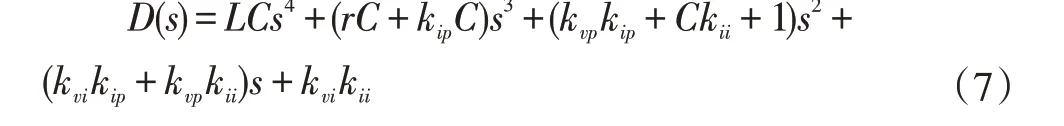
從上式可以看出此系統(tǒng)是一個四階系統(tǒng)，特征方程有四個根也就是說有四個閉環(huán)極點。使用伯德圖法、根軌跡法等一般方法設(shè)計雙閉環(huán)控制器時需要考慮調(diào)節(jié)器之間的響應(yīng)速度、頻帶寬度等多方面因素的互相影響，控制器設(shè)計步驟復雜，人工計算量大，而且還需反復湊驗；使用極點配置法不僅簡化設(shè)計過程還可減少人工計算量，而且所設(shè)計的參數(shù)能滿足系統(tǒng)高性能指標要求。

則由期望的主導極點與非主導極點所得閉環(huán)方程為：

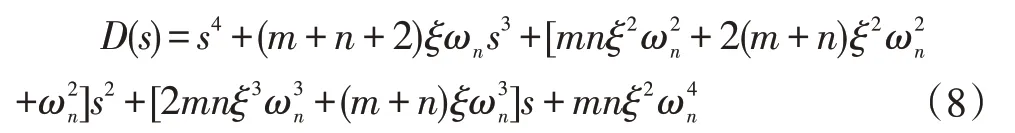
對比式（7）和式（8），令對應(yīng)系數(shù)相等，可得：

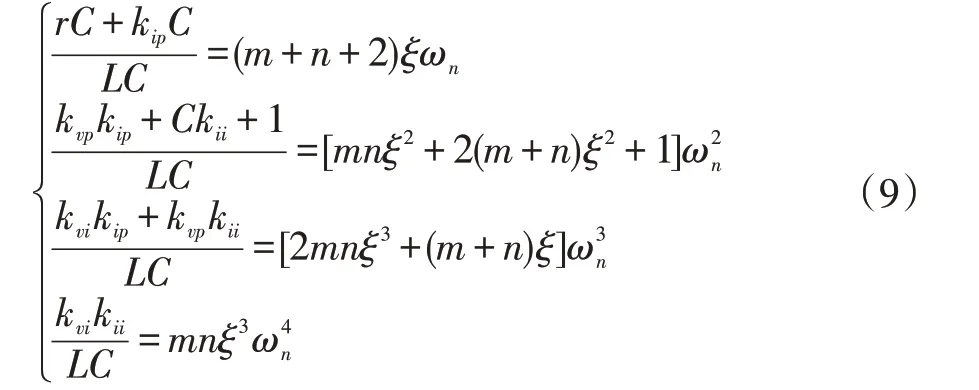
為使得計算方便，現(xiàn)令：

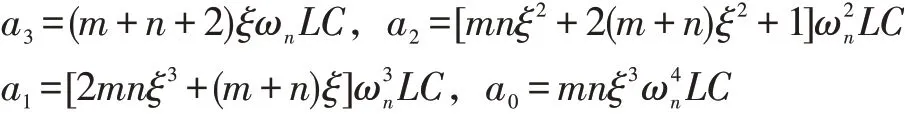
聯(lián)立上式可求得：

其中，根據(jù)kip的值可以求出式（10）的解，而kii即為該式的正實數(shù)根。

3 三相逆變器的仿真

根據(jù)上述分析，對三相逆變器的數(shù)學建模以及控制策略進行計算，利用MATLAB/Simulink 仿真平臺搭建逆變系統(tǒng)的仿真模型，對三相逆變器進行仿真，驗證控制策略的可行性與有效性。

3.1 濾波器參數(shù)設(shè)計

本文所設(shè)計的逆變器是通過以SVPWM 為控制信號來控制開關(guān)器件的通斷將直流輸入電壓轉(zhuǎn)換為正弦波等效的波形輸出，所以輸出電壓中包含有較多的高次諧波。為了使逆變器帶上負載后輸出能得到平滑的、波形質(zhì)量好的輸出電壓，因此必須在負載前端加低通濾波器以消除高次諧波分量，通常釆用LC 濾波器。

根據(jù)工程實踐，濾波器自身電感與電容的計算公式如下：

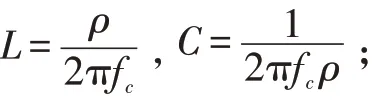
其中fc為濾波器的截止頻率，一般取為逆變器開關(guān)頻率的0.04-0.1 倍，ρ 為逆變器自身等效阻抗，一般取額定負載的0.4-0.8 倍。

綜合考慮整個逆變器的諧波輸出大小、控制算法及電感壓降等因素，通過計算，選取濾波器的電感值為2mH，濾波器的電容值為6 μF。三相逆變器的阻尼比c為ξ=，諧振頻率為ωn=所以，控制器參數(shù)可以計算得出：電壓環(huán)控制器參數(shù)：kvp=2.64e-3，kvi=1431；電流環(huán)控制器參數(shù)：kip=5.896，kii=356.394。

3.2 Simulink仿真分析

根據(jù)前面所給的系統(tǒng)參數(shù)，搭建仿真模型，對三相逆變器在不同工況下進行仿真。仿真結(jié)果如下。

（1）額定負載：Ra=Rb=Rc=6Ω，仿真結(jié)果如圖5所示，由波形圖可以看出，所搭建的電壓電流雙閉環(huán)系統(tǒng)模型有較好的輸出波形質(zhì)量。

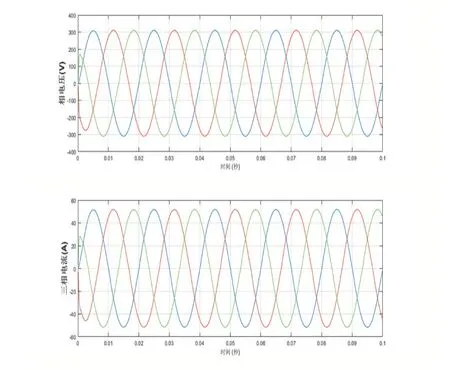
圖5 閉環(huán)穩(wěn)定工況時，輸出電壓和電流波形

（2）負載突變：在0.05s 時設(shè)置使得負載發(fā)生突變，此時Ra=Rb=Rc=3Ω，仿真結(jié)果如圖6 所示，該逆變系統(tǒng)的輸出電壓電流波形在0.05s 負載發(fā)生突變時，電壓電流均有輕微波動，但是在極短的時間內(nèi)即可恢復穩(wěn)定。

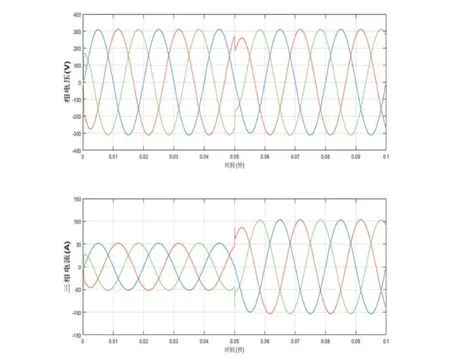
圖6 閉環(huán)負載突變時，輸出電壓和電流波形

（3）直流電壓源突變：在0.05s 時設(shè)置使得直流源發(fā)生突變，如圖7 所示，其中（a）圖為直流源從1500V瞬間增加到1800V 時的波形，（b）圖為直流源從1500V瞬間減小到1200V 時的波形，從仿真結(jié)果來看，輸出電壓均能在極短的時間內(nèi)回復到正常水平。

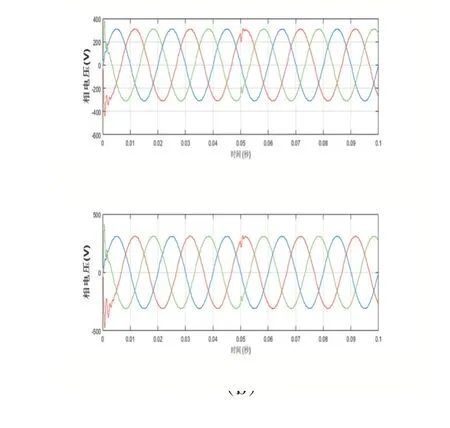
圖7 閉環(huán)直流電壓源突然增大和減小時，輸出電壓波形

經(jīng)過上述波形圖分析可知，采用以電容電流為內(nèi)環(huán)的雙閉環(huán)為控制策略之后，無論是負載發(fā)生突變或者是直流源發(fā)生突變的情況，輸出波形均能在很短的時間穩(wěn)定下來，說明該系統(tǒng)是穩(wěn)定的。

4 結(jié)語

本文主要研究了三相逆變系統(tǒng)的閉環(huán)控制系統(tǒng)。著重的研究逆變器在靜止和旋轉(zhuǎn)坐標系下的數(shù)學模型，推導傳遞函數(shù)計算系統(tǒng)穩(wěn)定性。最后在前文理論分析的基礎(chǔ)上，基于仿真工具MATLAB/Simulink 搭建輔助逆變器系統(tǒng)實驗平臺。對文中提出的逆變器電壓控制方法進行負載投切實驗、直流源突變的仿真實驗，結(jié)果完全符合設(shè)計要求。