超聲橢圓振動切削軌跡變化對表面形貌的影響

江禹安，皮鈞,2，楊光，姜濤，沈志煌

(1.集美大學 機械與能源工程學院, 福建 廈門 361021; 2.海洋平臺保障系統關鍵技術福建省高校工程研究中心，福建 廈門 361021)

0 引言

超聲橢圓振動切削最早由Shamoto等[1]提出，相對于普通切削，超聲橢圓振動切削由于自身特定的運動軌跡而具有優良的材料去除特性，包括使金屬材料呈現鏡面[2]、延長刀具使用壽命[3]、抑制毛刺[4]等。在實際加工中超聲橢圓振動切削軌跡形狀受兩相激勵相位差、振幅、刀具形狀和進給量等影響，從而影響加工質量。何俊等[5]通過仿真表明相位差為90°時平均切削力最小，切削效果最理想；李勛等[6]研究進給方向和切削方向殘余高度的影響因素，闡述了超聲橢圓振動切削表面形貌形成機理；Zhang等[7]主要研究橢圓軌跡中刃口鈍圓半徑對切削質量的影響，并建立了相應的模型。

目前針對刀尖橢圓振動切削軌跡形狀、軌跡偏轉變化對加工表面形貌的研究少有報道，探究橢圓振動切削軌跡變化，并通過雙通道超聲波發生器控制相位差分析橢圓振動切削軌跡變化對加工表面形貌的影響，對研究超聲橢圓振動超精密切削自由曲面具有非常重要的意義。

因此，本文通過建立橢圓振動切削軌跡變化切削方向殘余高度模型和動態切入角變化對加工表面質量的影響模型，分析橢圓振動切削軌跡變化對加工表面形貌的影響，并通過試驗驗證及探究最優加工表面質量的相位差值。

1 圓柱導波超聲橢圓振動系統

1.1 可控橢圓振動切削系統

已有的二維超聲振動切削系統[8-12]基本都是基于換能器與工具頭的剛性連接。剛性連接在兩個方向產生的聲阻抗相互作用無法正交輸出，導致兩個方向的振動模態耦合結果較差[13]，不能精準控制橢圓振動切削軌跡。

本實驗應用的導波傳輸超聲橢圓振動切削裝置[13]由雙通道超聲波發生器、功率放大器、夾心式壓電換能器、導波線和彎- 縱工具頭組成。如圖1所示，雙通道超聲波發生器通過功率放大器放大信號給兩組夾心式壓電換能器輸入頻率相同且具有一定相位差的高頻正弦激勵，縱振的夾心式壓電換能器連接水平方向的導波線，使得彎- 縱工具頭發生縱向振動；連接垂直方向的導波線使得彎- 縱工具頭發生彎曲振動。兩個正交方向的振動耦合到工具頭的刀尖上，最終疊加合成橢圓振動切削軌跡。由于導波線的軸向振動剛度遠大于彎曲剛度特性，使得兩個方向軸向振動耦合到彎- 縱工具頭；而較弱的彎曲剛度又會產生極小的聲阻抗，不影響彎- 縱工具頭的縱彎模態，保證了刀尖的正交振動輸出，從而通過調節相位差可達到刀尖橢圓振動切削軌跡精準調控，實現高精度橢圓振動切削軌跡變化。

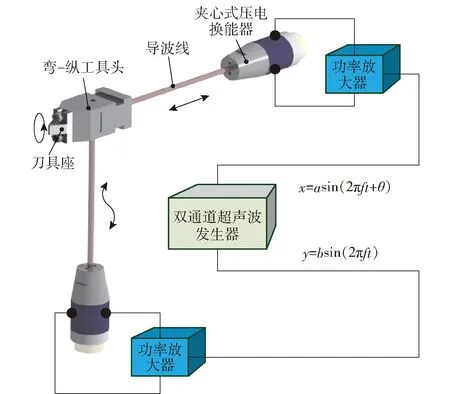
圖1 導波傳輸超聲橢圓振動切削裝置Fig.1 Ultrasound elliptic vibration cutting device with guided wave transmission

1.2 橢圓振動切削軌跡的控制

將橢圓振動切削軌跡在Oxy平面內分解成相互垂直且頻率相同、具有一定相位差的兩個簡諧運動，運動軌跡方程為

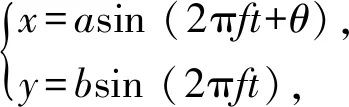
(1)

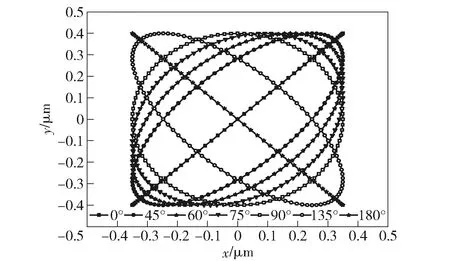
圖2 不同相位差的橢圓振動切削軌跡Fig.2 Elliptic vibration cutting trajectories with different phase differences

式中：θ為相位差；f為振動頻率；a、b分別為x軸方向振幅和y軸方向振幅，通過控制其振幅和相位差就可以實現橢圓振動切削軌跡的形狀和偏轉變化。若只對相位差控制則可得到刀尖橢圓振動切削軌跡(見圖2)。

2 橢圓振動切削軌跡變化分析

2.1 橢圓振動切削軌跡產生的切削特性

圖3為僅改變相位差得到的3種不同相位差的刀尖橢圓振動切削軌跡，圖中Rth1、Rth2、Rth3分別為相位差90°、75°、30°的切削方向殘余高度，γ1、γ2、γ3分別為相位差90°、75°、30°的動態切入角。從幾何學分析可知，相位差為90°時切削方向殘余高度Rth1最小，動態切入角γ1也最小。但過小的動態切入角使得刀具的動態鋒利程度降低，動態切削力加大。所以在控制切削方向殘余高度值的情況下適當增加動態切入角，更有利于提高實際加工表面質量。

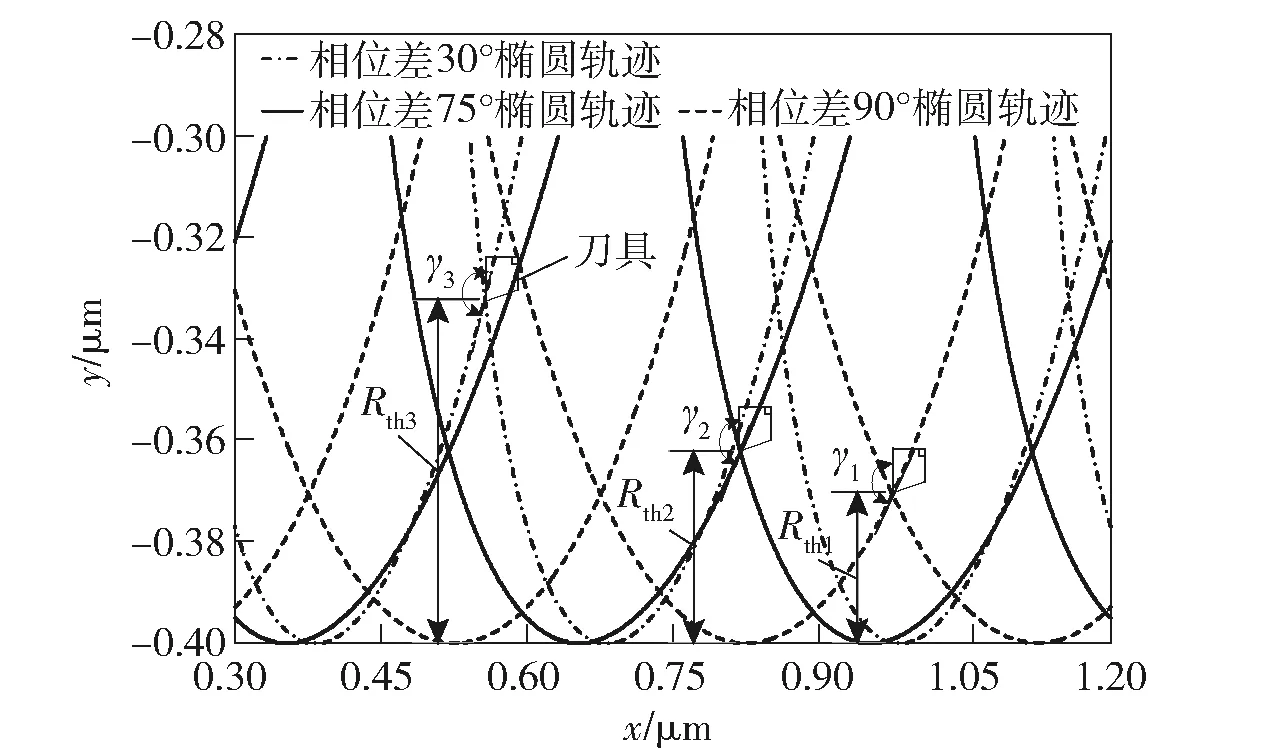
圖3 橢圓振動切削的運動特征Fig.3 Motion characteristics of elliptic vibration cutting

2.2 切削方向殘余高度模型

圖4 切削過程模型Fig.4 Cutting process model

按Zhang等[14]提出的圖4所示切削模型，推導切削方向殘余高度與振幅、相位差的關系。圖4中A0、A1為相鄰兩個切削軌跡的切削尖點；B點為切削的最低點；C點為刀具正在橢圓振動切削軌跡上的切削點；D點為刀具在橢圓振動切削軌跡上與工件的分離點；Rth為切削方向殘余高度；vs為x軸方向的相對切削速度；vt為瞬時速度矢量；β為瞬態速度角。

假設刀具在x軸、y軸方向按照橢圓振動切削軌跡移動，按(1)式可得刀具位置相對于靜止工件的表達式：

(2)

根據圖4可得

(3)

式中：t0、t1為切削尖點A0和A1對應的時間；ω=2πf；2πvs/ω為A0到A1點的距離。將(2)式代入(3)式，得

(4)

參考Shamoto等[1]的方法，可得

Rth=bcos (ωt0+θ)+b.

(5)

由(5)式可知，切削方向殘余高度與縱向振幅、頻率、相位差等有關，但并沒有表達出殘余高度與相對切削速度的關系。

如圖5所示，提出另一種切削方向殘余高度計算模型，其中Oxy平面內橢圓為當前周期的振動切削軌跡；O1x1y1平面內橢圓為下一個周期的振動切削軌跡。利用橢圓形狀表達式求得切削方向殘余高度[15]的表達式為

(6)

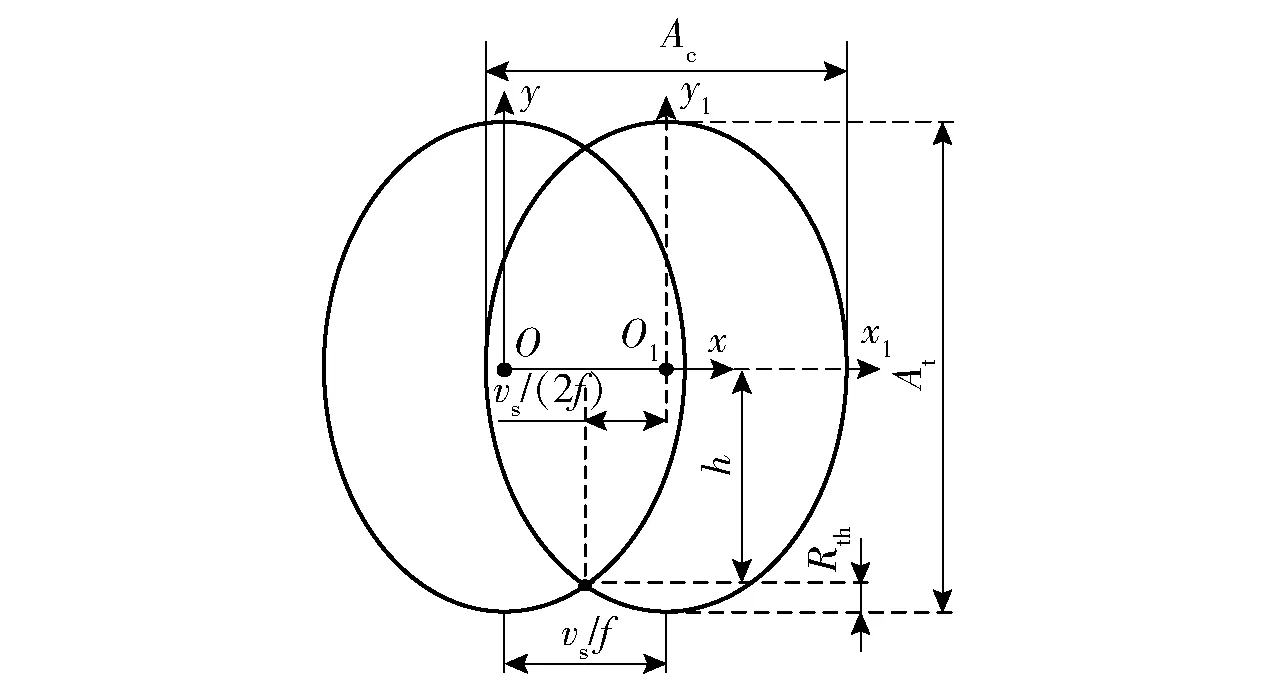
圖5 切削方向殘余高度模型Fig.5 Residual height model in cutting direction

式中：h為前后兩個周期橢圓軌跡交點與x軸的距離；At為y軸方向振幅的2倍；Ac為x軸方向振幅的2倍。

按照Kurniawan等[16]提出的速度比概念：切削速度與最大振動速度(臨界切削速度)的比值，即速度比SR滿足：

SR=vs/(2πfa).

(7)

為了實現刀具與工件表面的分離，SR必須小于1[17]. 因為SR小于1，所以fAc/vs大于1. 利用泰勒級數變換，當fAc/vs遠大于1時，殘余高度近似為

(8)

由(8)式可知切削方向殘余高度與縱向振幅和相對切削速度的平方呈正比，與橫向振幅的平方和頻率的平方呈反比。

2.3 橢圓振動切削軌跡偏轉對殘余高度的影響

根據2.2節的分析，切削方向殘余高度模型并沒有考慮橢圓振動切削軌跡偏轉的影響。

圖6為橢圓振動切削軌跡偏轉圖。由圖6可見，在Oxy平面內圖中正橢圓振動切削軌跡P1變換為斜橢圓振動切削軌跡P2，偏轉角為η. 同理，在O1x1y1平面內P′1變換為P′2. 相對于自身的坐標系，兩個橢圓振動切削軌跡對應的振幅完全一樣，其中b≥a. 但相對于正坐標系，變換后斜橢圓振動切削軌跡的振幅為m、n. 其中θ和m、n3個特征值是確定橢圓振動切削軌跡偏轉的基本參數。由(2)式求得θ、m、n[18]分別為

(9)

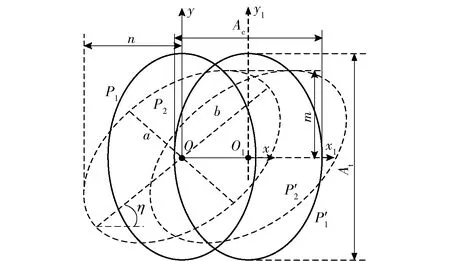
圖6 橢圓振動切削軌跡偏轉Fig.6 Elliptic vibration cutting trajectory deflection

將(9)式代入(8)式，求得橢圓振動切削軌跡偏轉下切削方向殘余高度為

(10)

當偏轉角度η>90°時，(9)式中振幅a、b存在限制，部分成立，因此偏轉角度需滿足0°≤η≤90°. 將模擬參數a=3.5 μm、b=4 μm、vs=2.0 m/s、f=100 kHz代入(9)式和(10)式，得到偏轉角度和它們的關系。

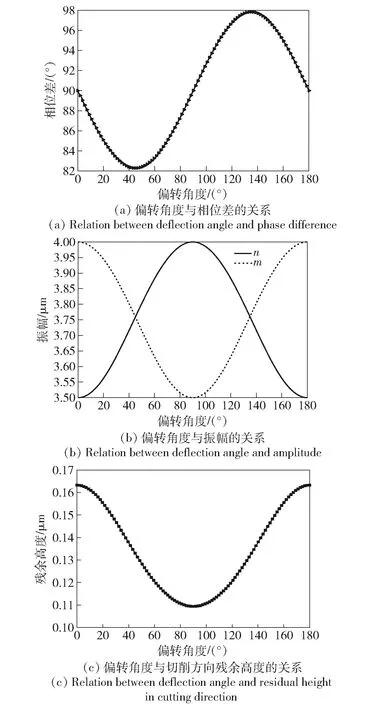
圖7 橢圓振動切削軌跡偏轉參數關系圖Fig.7 Relational graph of deflection parameters of elliptic vibration cutting trajectory

圖7為橢圓振動切削軌跡偏轉參數關系圖。當需要改變橢圓振動切削軌跡時，根據圖7(a)中偏轉角度確定相位差值，再根據圖7(b)確定對應的振幅，即可實現橢圓振動切削軌跡偏轉變化。圖7(c)為偏轉角度與切削方向殘余高度的關系，當偏轉角度為90°時，殘余高度最小。

3 橢圓振動切削實驗

3.1 切削裝置及條件

由于暫時不能精準控制振幅變化，目前僅能通過調節相位差研究單一因素對加工表面的影響。實驗采用自行研制的導波傳輸超聲橢圓振動切削裝置，并設置相位差0°、30°、45°、60°、75°、90°、120°、135°、150°、180° 10組實驗。圖8為超聲橢圓振動切削系統加工平臺，圖中u為工件切削方向；v為工件進給方向(下同)。

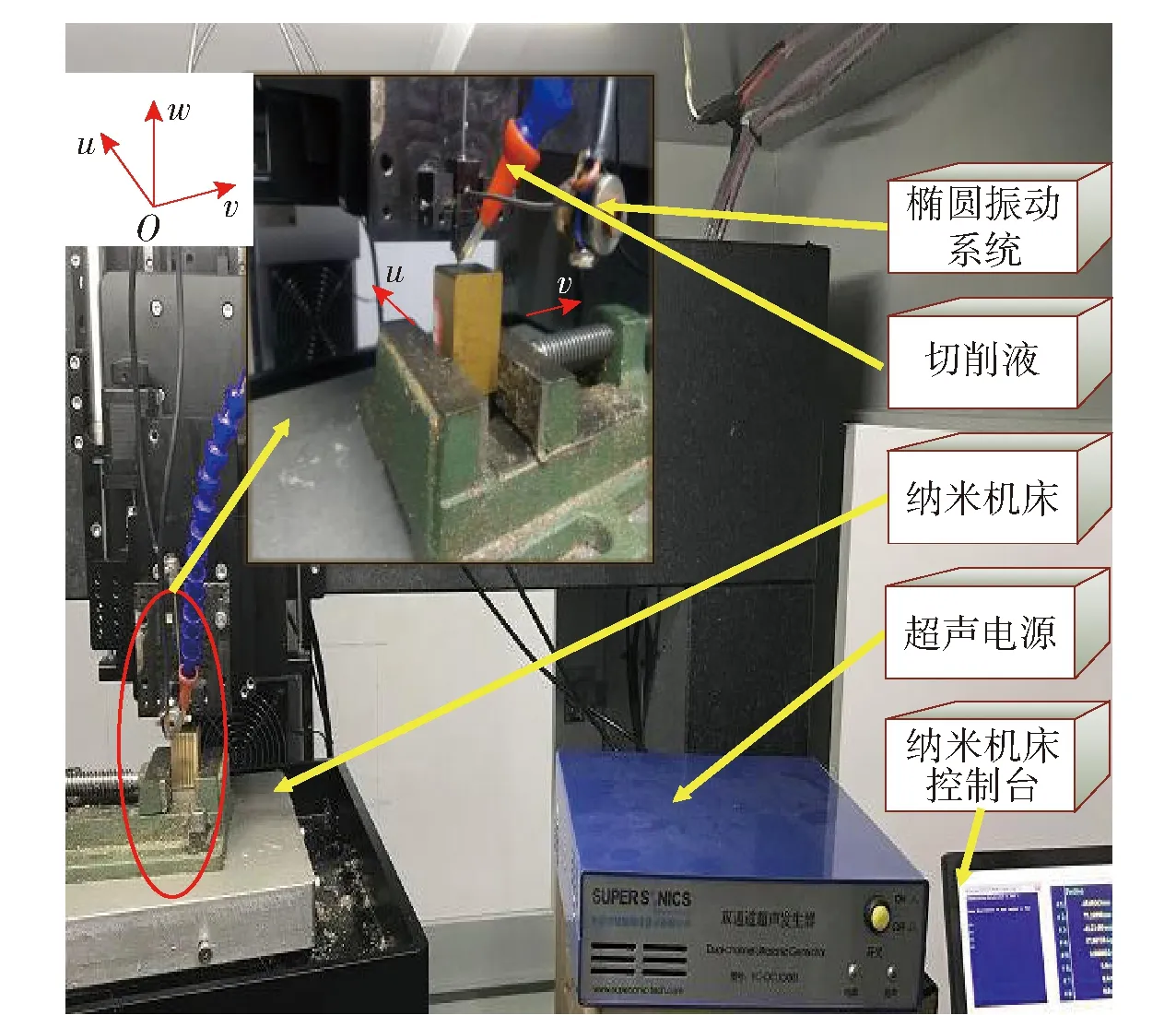
圖8 超聲橢圓振動切削系統加工平臺Fig.8 Machining platform of ultrasound elliptic vibration cutting device

刀尖振動參數：u向振幅為0.4 μm、w向振幅為0.35 μm、振動頻率為104 kHz，因此臨界切削速度為0.228 m/s. 切削材料為黃銅，切削方式為刨削，切削參數如表1所示。

表1 切削參數

注：進給量0.5 μm是加工表面達到鏡面效果的切削參數。

刀具形狀如圖9所示，刀具夾角為65°，材質為單晶金剛石，刀具參數如表2所示。

3.2 加工表面質量分析

圖10(a)、圖10(b)和圖10(c)是利用日本基恩士公司產VK-X100K激光共聚焦顯微鏡測得相位差為0°、75°和90°時的加工表面形貌。在相位差0°時由于切削方向殘余高度理論值最大且刀尖動態切入角過大，在切削方向會向兩側擠壓，造成刀痕斷續；在相位差90°時刀痕斷續和兩側擠壓相對減小，但是會隔一段距離產生，因為在實際的超聲橢圓振動切削中，相位差90°時刀具與切屑的摩擦力反轉變成有利于切屑流出的提拉力效果最大，能減少刀痕斷續和兩側擠壓，獲得較好的表面質量；在相位差75°時得到最佳切削表面質量，刀痕變得十分有規律，材料兩側的擠壓效應明顯減少，由圖10(d)可以直觀看到材料表面達到鏡面狀態，這是因為在相位差75°時切削方向殘余高度理論值較小，并且能適當提高動態切入角，保證刀具獲得較好的切入狀態。

圖9 刀具形狀Fig.9 Tool shape

刀尖圓弧半徑/μm前角/(°)后角/(°)356

圖10 切削表面形貌Fig.10 Cutting surface morphologies under various phase differences

圖11為實際測得切削方向殘余高度與相位差的關系，隨著相位差的增大，殘余高度先減小、后增大。

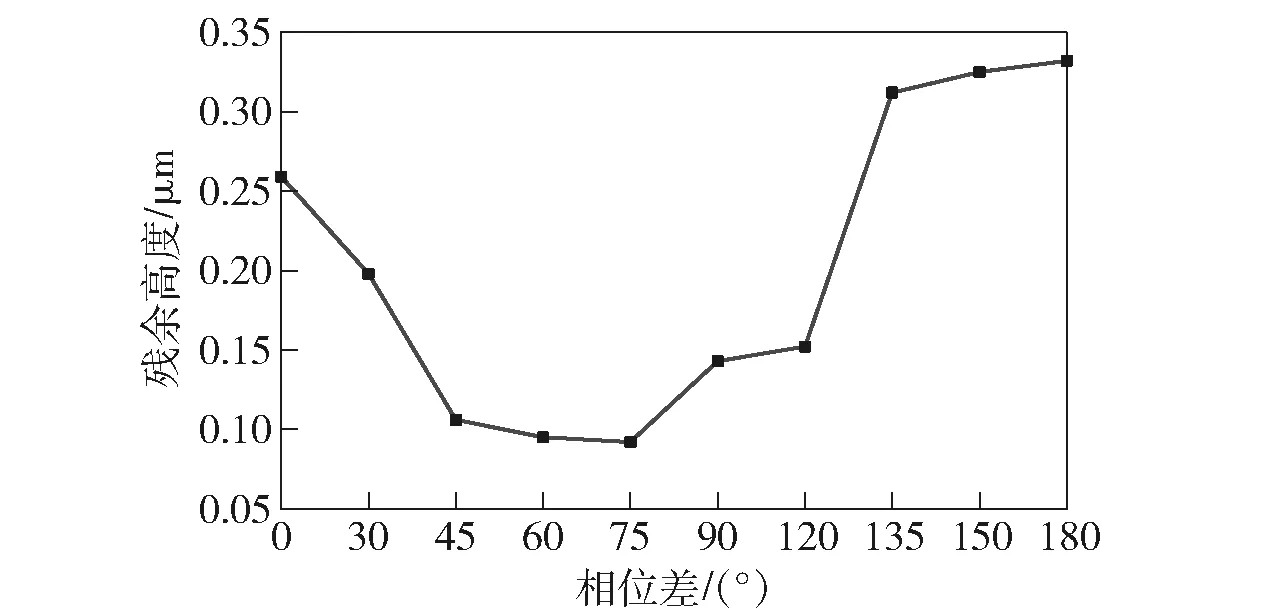
圖11 殘余高度與相位差的變化規律Fig.11 Variation law of residual height and phase difference

表3為3種相位差下材料的表面粗糙度對比，在相位差75°時進給方向與切削方向的表面粗糙度都是最小。

表3 表面粗糙度對比

圖12(a)為0°相位差時加工的微三棱錐；圖12(b)為75°相位差時加工的微三棱錐，圖中Ⅰ、Ⅱ、Ⅲ是微三棱錐加工成形的3個表面。圖12(a)中的微三棱錐3個面和棱邊存在不同程度的毛刺和崩邊，而圖12(b)的加工對于毛刺和崩邊抑制起到了很好的作用。

圖12 微三棱錐電鏡觀測圖Fig.12 Electron microscopical images of micro-triangular pyramids

4 結論

本文基于研制的導波傳輸超聲橢圓振動切削裝置，建立了橢圓振動切削軌跡變化切削方向殘余高度模型和動態切入角變化對加工表面質量的影響模型。通過理論分析和實驗對比，主要得到以下結論：

1)超聲橢圓振動切削軌跡的偏轉變化同時引起切削方向殘余高度和刀具動態切入角變化，是導致切削表面質量改變的重要因素。

2)相位差增大，殘余高度先減小、后增大，加工過程中存在一個最優相位差值。通過微三棱錐切削實驗證明，對毛刺和崩邊的抑制也存在同樣規律。

3)建立的模型為研制精準可控的橢圓軌跡控制系統提供了理論基礎，對研究軌跡變化在復雜曲面光學元件加工中的應用具有重要意義。