一種分布式多無人機(jī)協(xié)同定距盤旋跟蹤制導(dǎo)律

馮運(yùn)鐸，吳炎烜，曹昊哲

(北京理工大學(xué) 機(jī)電學(xué)院, 北京 100081)

0 引言

近些年來，無人機(jī)發(fā)展迅速，其隱蔽性好、生命力強(qiáng)、造價(jià)低廉等特點(diǎn)以及對地面和空中目標(biāo)的定距追蹤能力，使其在偵察監(jiān)視、搜索救護(hù)等領(lǐng)域有著廣泛應(yīng)用[1-2]。不同于旋翼無人機(jī)，固定翼無人機(jī)需要維持一定的巡航速度，因此當(dāng)跟蹤的目標(biāo)速度較低時(shí)，固定翼無人機(jī)通常采用定距盤旋的方式跟蹤目標(biāo)。相比于攜帶探測設(shè)備能力有限的單架無人機(jī)，多無人機(jī)組成編隊(duì)對目標(biāo)進(jìn)行協(xié)同包圍追蹤具有以下優(yōu)勢：可以擴(kuò)大對目標(biāo)的探測感知范圍，避免因視線被阻擋造成的目標(biāo)丟失等情況；編隊(duì)包圍目標(biāo)，可以從不同方位獲取目標(biāo)信息，提高了對目標(biāo)狀態(tài)的估計(jì)精度。

根據(jù)無人機(jī)定距盤旋跟蹤制導(dǎo)律所利用的相對信息不同，將制導(dǎo)策略大致分為3類：基于視線角與視線角速率的制導(dǎo)策略[3-5]、基于相對距離與相對距離變化率的制導(dǎo)策略[6-8]和基于相對距離與視線角的制導(dǎo)策略[9-10]。其中基于視線角與視線角速率的制導(dǎo)策略在多無人機(jī)的定距盤旋問題中最為常見，其通過將無人機(jī)簡化為1階或2階積分器，將視線角信息轉(zhuǎn)化為由無人機(jī)指向目標(biāo)的向量，從而把多無人機(jī)系統(tǒng)的穩(wěn)定性問題轉(zhuǎn)化為線性代數(shù)問題進(jìn)行分析，利用多無人機(jī)系統(tǒng)的狀態(tài)方程結(jié)合拉普拉斯矩陣的性質(zhì)對問題進(jìn)行求解。例如Boccia等[11]僅利用角度信息實(shí)現(xiàn)了多無人機(jī)對目標(biāo)的協(xié)同定距盤旋。且這種方法與分析多旋翼無人機(jī)系統(tǒng)的方法類似[12-15]，例如文獻(xiàn)[12]中針對具有切換拓?fù)涞男頍o人機(jī)時(shí)變編隊(duì)跟蹤控制問題，基于2階積分器提出了基于鄰近無人機(jī)信息的編隊(duì)跟蹤協(xié)議以及相應(yīng)的系統(tǒng)穩(wěn)定充分必要條件，利用李雅普諾夫第2法證明系統(tǒng)穩(wěn)定性條件，并通過實(shí)驗(yàn)驗(yàn)證了協(xié)議的有效性，然而這種簡化模型并不符合固定翼無人機(jī)通過橫向滾轉(zhuǎn)改變飛行軌跡的運(yùn)動特性。與之相比，基于相對距離與相對距離變化率和基于相對距離與視線角的兩種制導(dǎo)策略中通常將固定翼無人機(jī)簡化為Unicycle模型[16-18]，更貼合實(shí)際。但是與此同時(shí)在無人機(jī)和目標(biāo)的相對運(yùn)動方程中引入了三角函數(shù)而使其變?yōu)榉蔷€性方程，增加了系統(tǒng)穩(wěn)定性證明的難度，因此一些文獻(xiàn)僅給出基于平衡點(diǎn)的線性系統(tǒng)穩(wěn)定性證明[19-20]。

Leader-Follower法是常用的多無人機(jī)編隊(duì)結(jié)構(gòu)[21-22]，作為Follower的無人機(jī)以Leader為中心節(jié)點(diǎn)構(gòu)成編隊(duì)，然而作為Leader的無人機(jī)損壞會導(dǎo)致整個(gè)編隊(duì)解體。相比之下，分布式編隊(duì)結(jié)構(gòu)具有以下優(yōu)點(diǎn)[23]：無人機(jī)個(gè)體間的地位相同，即使某架損壞也不會影響編隊(duì)，提高了編隊(duì)網(wǎng)絡(luò)魯棒性；當(dāng)有新的無人機(jī)個(gè)體加入編隊(duì)時(shí)，由于只與其鄰近個(gè)體聯(lián)系，不會過度影響整體編隊(duì)網(wǎng)絡(luò)，編隊(duì)可擴(kuò)展性更好；降低了對無人機(jī)之間通信網(wǎng)絡(luò)帶寬的要求。

綜上所述可知多固定翼無人機(jī)協(xié)同定距盤旋追蹤目標(biāo)的難點(diǎn)在于：1)如何基于符合固定翼無人機(jī)運(yùn)動特性的Unicycle模型而非2階積分器設(shè)計(jì)協(xié)同追蹤制導(dǎo)律，使其具有實(shí)際的應(yīng)用價(jià)值，并證明多無人機(jī)系統(tǒng)的穩(wěn)定性；2)如何采用分布式而非Leader-Follower的編隊(duì)結(jié)構(gòu)，使多架無人機(jī)定距盤旋跟蹤目標(biāo)的同時(shí)組成具有較強(qiáng)魯棒性的編隊(duì)，當(dāng)編隊(duì)中無人機(jī)損壞時(shí)其余無人機(jī)能夠保持隊(duì)形，當(dāng)有新無人機(jī)加入時(shí)能夠形成新的編隊(duì)。

本文采用基于相對距離與視線角的制導(dǎo)策略，提出了一種分布式多無人機(jī)協(xié)同定距盤旋追蹤低速目標(biāo)的制導(dǎo)方法。首先以Unicycle模型為基礎(chǔ)，考慮固定翼無人機(jī)的橫向運(yùn)動特性，設(shè)計(jì)了一種針對靜止目標(biāo)的分布式協(xié)同定距盤旋制導(dǎo)律，使多架無人機(jī)在繞靜止目標(biāo)盤旋的同時(shí)以一定的隊(duì)形包圍目標(biāo)，并給出系統(tǒng)穩(wěn)定性證明；然后將該制導(dǎo)律推廣至對勻速運(yùn)動和變速運(yùn)動目標(biāo)的跟蹤制導(dǎo)；最后通過半實(shí)物仿真，驗(yàn)證了本文設(shè)計(jì)制導(dǎo)律的有效性。

1 固定翼無人機(jī)定距跟蹤問題描述

無人機(jī)飛行控制系統(tǒng)由內(nèi)回路(穩(wěn)定回路)和外回路(制導(dǎo)回路)組成，且本文假設(shè)內(nèi)回路已經(jīng)設(shè)計(jì)完成，能夠很好地響應(yīng)外回路制導(dǎo)指令。固定翼無人機(jī)通常將內(nèi)、外回路控制系統(tǒng)分解為垂直平面和水平平面兩個(gè)通道，在垂直平面通過升降舵和推力系統(tǒng)調(diào)整無人機(jī)的飛行高度和速度，在水平平面通過副翼與方向舵控制無人機(jī)的水平航跡。在實(shí)際應(yīng)用中，當(dāng)處于平飛狀態(tài)的無人機(jī)速度或者滾轉(zhuǎn)角變化時(shí)，無人機(jī)的飛行高度會受到影響，但是在速度和滾轉(zhuǎn)角變化的同時(shí)，及時(shí)調(diào)整升降舵能夠使其飛行高度的變化較小，此時(shí)可以近似地認(rèn)為無人機(jī)始終在同一高度飛行，因此本文中僅考慮多無人機(jī)在水平平面的編隊(duì)問題。在不考慮無人機(jī)垂直方向上的運(yùn)動和氣動性能、飛行狀況等因素，即所有無人機(jī)保持相同高度飛行的情況下，考慮到固定翼無人機(jī)通過滾轉(zhuǎn)運(yùn)動改變速度方向的特性，對固定翼無人機(jī)建立運(yùn)動模型：

(1)

式中：xi、yi、ψi、vi分別為無人機(jī)i的二維平面坐標(biāo)、偏航角和速度(如未特殊說明，本文中的速度皆指速度大小)，i=1,2,3,…,n,n為無人機(jī)的數(shù)量；ui和wi為無人機(jī)i的控制輸入。假設(shè)目標(biāo)與無人機(jī)具有相同的運(yùn)動模型，且xt、yt、ψt、vt為分別為目標(biāo)的坐標(biāo)、偏航角和速度，ut和wt為目標(biāo)的輸入。

(2)

圖1 多無人機(jī)定距跟蹤示意圖Fig.1 Schematic diagram of tracking the targets by multi-UAVs

將無人機(jī)i和目標(biāo)之間的相對運(yùn)動方程寫為極坐標(biāo)形式：

(3)

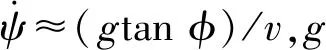
(4)

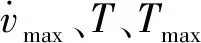
2 靜止目標(biāo)的協(xié)同定距盤旋算法

假設(shè)目標(biāo)處于靜止?fàn)顟B(tài)，即vt=0 m/s、ut=0 rad/s，則(3)式簡化為

(5)

考慮到實(shí)際情況下，固定翼無人機(jī)的內(nèi)回路通常將縱向和橫向平面分開考慮，且由(5)式可知其速度方程為1階積分器，則在(6)式的輸入作用下，無人機(jī)的速度會收斂至無人機(jī)的期望速度vc，其中kv為無人機(jī)速度通道的控制增益，由于kv不僅決定無人機(jī)的速度變化率，同時(shí)也影響速度通道的收斂速度，因此kv的取值需綜合考慮兩方面因素。

wi=kv(vc-vi).

(6)

在速度控制器的基礎(chǔ)上提出分布式多無人機(jī)定距盤旋制導(dǎo)律：

(7)

(8)

輸入ui代入(5)式，可得無人機(jī)i的視線角狀態(tài)方程為

(9)

證明：

(10)

式中：Ln×n=[lij]為拉普拉斯矩陣，其形式見(11)式，由文獻(xiàn)[24-25]可知其特征值為λL≥0:

(11)

作如下線性變換:y=χ-Kχc，則

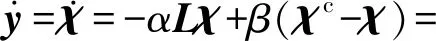
其中K為n階矩陣，I為n階單位矩陣，求解矩陣(αL+βI)的特征值λ：

由于α和β都是正實(shí)數(shù)且λL≥0，則類比拉普拉斯矩陣L的特征方程可得矩陣(αL+βI)的特征值λ：

λ=αλL+β>0.

(12)

因?yàn)?(αL+βI)的特征值均小于0，所以系統(tǒng)最終會收斂至y→0即χ→Kχc，所有無人機(jī)的視線角最終會收斂至定值Kχc，即所有無人機(jī)期望視線角的加權(quán)和。

證明：

(13)

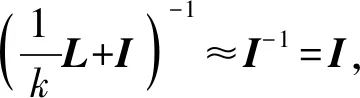
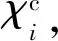
(14)

式中：vc為無人機(jī)的期望速度。

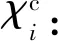
令整個(gè)多無人機(jī)系統(tǒng)的能量函數(shù)H為

(15)

將其對時(shí)間求導(dǎo)，得

(16)

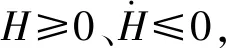
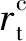
(17)

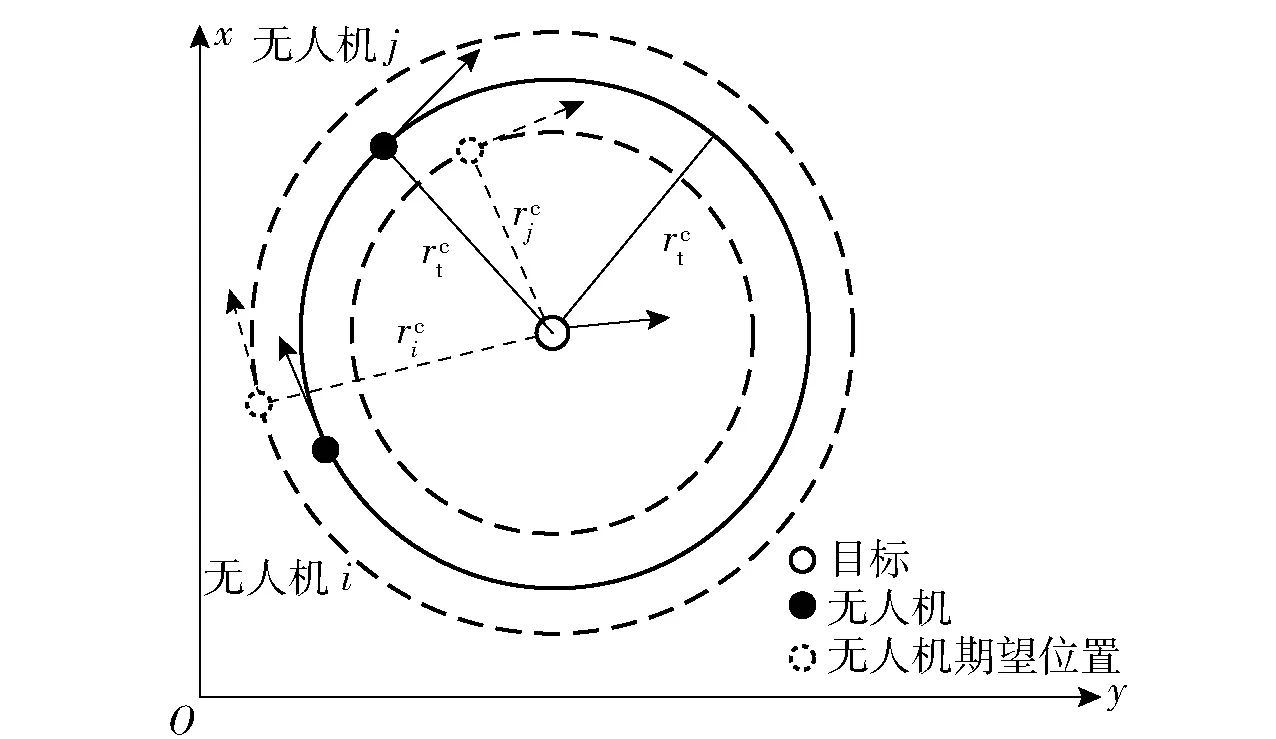
圖2 多無人機(jī)之間距離控制示意圖Fig.2 Control of distance between UAVs

3 運(yùn)動目標(biāo)的協(xié)同定距盤旋算法

當(dāng)目標(biāo)靜止時(shí)，無人機(jī)以相同的速度飛行即可完成協(xié)同定距盤旋。當(dāng)目標(biāo)以速度vt運(yùn)動時(shí)，相同速度的無人機(jī)雖然可以定距追蹤目標(biāo)，但由于無人機(jī)相對目標(biāo)的速度大小時(shí)刻變化，無人機(jī)之間的距離無法收斂至定值，多無人機(jī)無法形成編隊(duì)。針對此類情況，將無人機(jī)的速度矢量進(jìn)行如下分解：

(18)

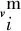
(19)

圖3 無人機(jī)速度分解示意圖Fig.3 Decomposition diagram of UAV speed

由于每架無人機(jī)的期望速度不再相同，將(6)式改寫為

(20)

在(20)式的輸入作用下，所有無人機(jī)相對目標(biāo)的速度大小收斂至相同值vc，則將無人機(jī)相對運(yùn)動目標(biāo)的運(yùn)動方程改寫為

(21)

(22)

(23)

若目標(biāo)為變速運(yùn)動狀態(tài)，此時(shí)目標(biāo)對時(shí)間的導(dǎo)數(shù)不再為0，則將(18)式寫成標(biāo)量形式：

(24)

(25)

上述從靜止目標(biāo)向運(yùn)動目標(biāo)的推導(dǎo)過程表明：對于運(yùn)動目標(biāo)，制導(dǎo)律的有效應(yīng)用需要引入額外信息，當(dāng)目標(biāo)勻速運(yùn)動時(shí)為目標(biāo)的速度信息，當(dāng)目標(biāo)變速運(yùn)動時(shí)為目標(biāo)的速度和加速度信息。本文中假設(shè)這些運(yùn)動信息皆是已知的，而在實(shí)際工程中難以直接測量目標(biāo)的速度和加速度，因此可以通過對目標(biāo)連續(xù)位置變化的分析間接得到其速度和加速度信息。例如基于光學(xué)成像的光流法能夠有效地獲得目標(biāo)的位置和速度信息[26]，基于機(jī)器學(xué)習(xí)的視覺識別能夠在先驗(yàn)知識的基礎(chǔ)上對目標(biāo)速度和加速度作出預(yù)測[27]。但是這種間接方法通常具有計(jì)算量大的缺點(diǎn)，對機(jī)載計(jì)算機(jī)的計(jì)算能力具有較高要求。

4 仿真驗(yàn)證

為驗(yàn)證前述算法的有效性，本節(jié)構(gòu)建如圖4所示的仿真框架，搭建基于飛行控制器、模擬飛行軟件X-Plane和仿真軟件MATLAB/Simulink的半實(shí)物仿真平臺，分別針對靜止、勻速和變速目標(biāo)的協(xié)同跟蹤定距盤旋制導(dǎo)律進(jìn)行仿真驗(yàn)證。其中飛行控制器作為內(nèi)回路控制無人機(jī)的飛行姿態(tài)，X-Plane軟件用來進(jìn)行固定翼無人機(jī)的動力學(xué)仿真，模擬無人機(jī)在現(xiàn)實(shí)中的飛行，而外回路制導(dǎo)模塊和通信模塊則在Simulink軟件下搭建完成。

圖4 仿真框架示意圖Fig.4 Simulation block diagram

假設(shè)無人機(jī)數(shù)量n=3，其初始時(shí)刻的位置、速度大小和航向角分別為UAV1={1 000 m,-900 m,40 m/s,π/4 rad}、UAV2={600 m,300 m,30 m/s,5π/4 rad}、UAV3={200 m,-200 m,20 m/s,3π/2 rad}。

綜上所得參數(shù)設(shè)置為

如圖5所示為半實(shí)物仿真中X-Plane軟件的顯示界面。為表現(xiàn)更直觀，以下只給出了二維平面的軌跡示意圖。

圖5 X-Plane軟件的三維仿真圖Fig.5 3D simulation of X-Plane software

4.1 靜止目標(biāo)

為與前述無人機(jī)初始狀態(tài)數(shù)據(jù)構(gòu)型相同，假設(shè)目標(biāo)的初始狀態(tài)為TARGETs={500 m,353 m,0 m/s,0 rad}。

設(shè)無人機(jī)的期望速度vc=30 m/s，如圖6、圖7和圖8所示分別為3架無人機(jī)協(xié)同繞靜止目標(biāo)定距盤旋的軌跡圖、距離變化曲線圖和相對速度變化示意圖，可以看出初始時(shí)刻無人機(jī)3距離目標(biāo)較近，無人機(jī)1和無人機(jī)2距離目標(biāo)較遠(yuǎn)。在150 s以內(nèi)，無人機(jī)和目標(biāo)的距離和視線角以及無人機(jī)之間的距離最終收斂至預(yù)設(shè)值，3架無人機(jī)以正三角形隊(duì)形包圍目標(biāo)，且無人機(jī)的速度在較短的時(shí)間內(nèi)收斂至期望值。

圖6 跟蹤靜止目標(biāo)軌跡圖Fig.6 Tracking trajectory for stationary target

圖7 距離變化示意圖(靜止目標(biāo))Fig.7 Distances among UAVs (stationary target)

圖8 相對速度變化示意圖(靜止目標(biāo))Fig.8 Relative speeds of UAVs (stationary target)

4.2 勻速運(yùn)動目標(biāo)

假設(shè)目標(biāo)的初始狀態(tài)為TARGETc={500 m,353 m,10 m/s,0 rad}。

設(shè)無人機(jī)相對目標(biāo)運(yùn)動的期望速度vc=30 m/s，如圖9、圖10和圖11所示為3架無人機(jī)協(xié)同追蹤勻速運(yùn)動目標(biāo)的軌跡圖、距離變化曲線圖和相對速度變化示意圖，可以看出3架無人機(jī)仍能以預(yù)定隊(duì)形定距追蹤目標(biāo)，即無人機(jī)和目標(biāo)之間的距離以及無人機(jī)之間的距離最終穩(wěn)定在預(yù)設(shè)值。雖然無人機(jī)相對目標(biāo)的速度仍然收斂至期望值，但是與目標(biāo)靜止時(shí)相比，相對速度收斂得較慢。

圖9 跟蹤勻速運(yùn)動目標(biāo)軌跡Fig.9 Tracking trajectory for target with constant speed

圖10 距離變化示意圖(勻速目標(biāo))Fig.10 Distances among UAVs (target with constant speed)

圖11 速度變化示意圖(勻速目標(biāo))Fig.11 Relative speeds of UAVs (target with constant speed)

4.3 變速運(yùn)動目標(biāo)

假設(shè)目標(biāo)的初始狀態(tài)為TARGETt={500 m,353 m,5 m/s,0 rad}。

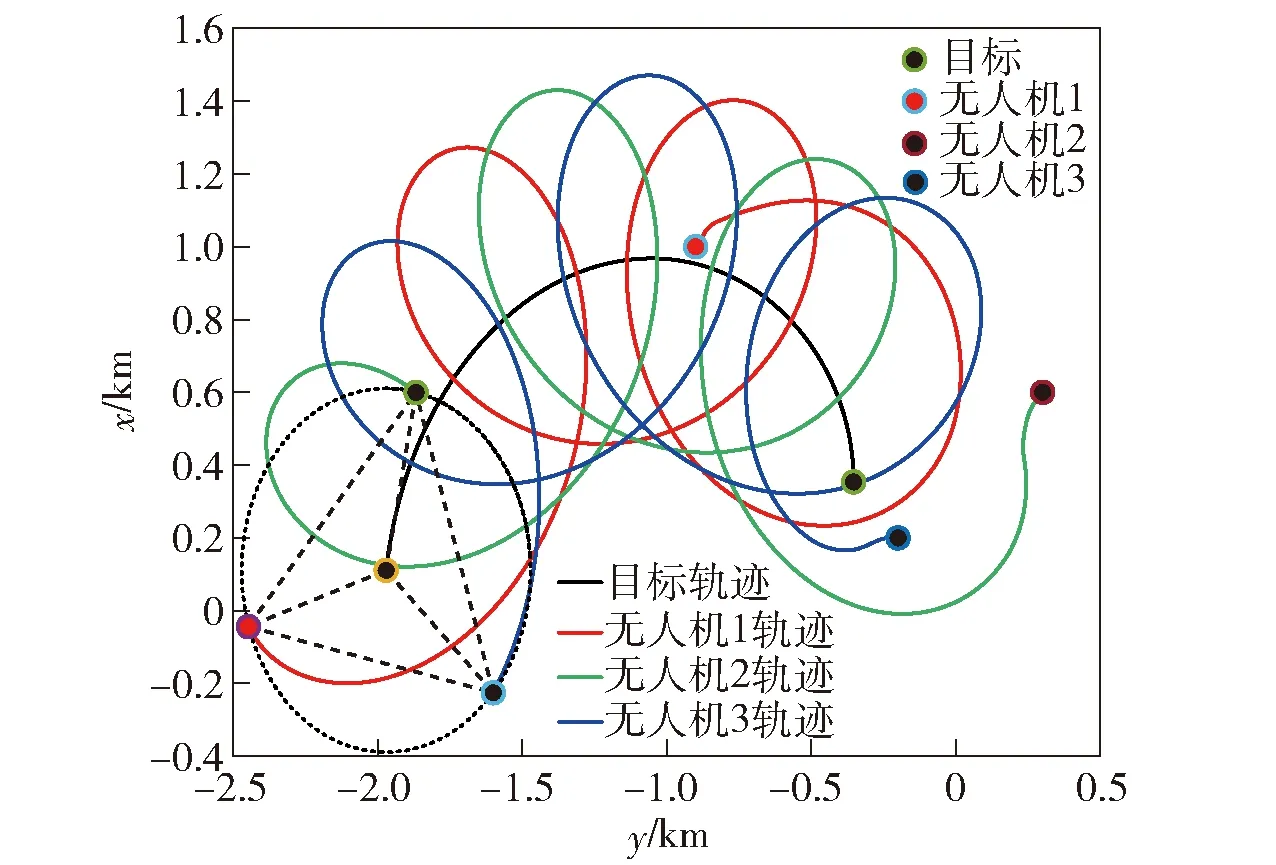
圖12 跟蹤變速運(yùn)動目標(biāo)軌跡圖Fig.12 Tracking trajectories for target with variable speed

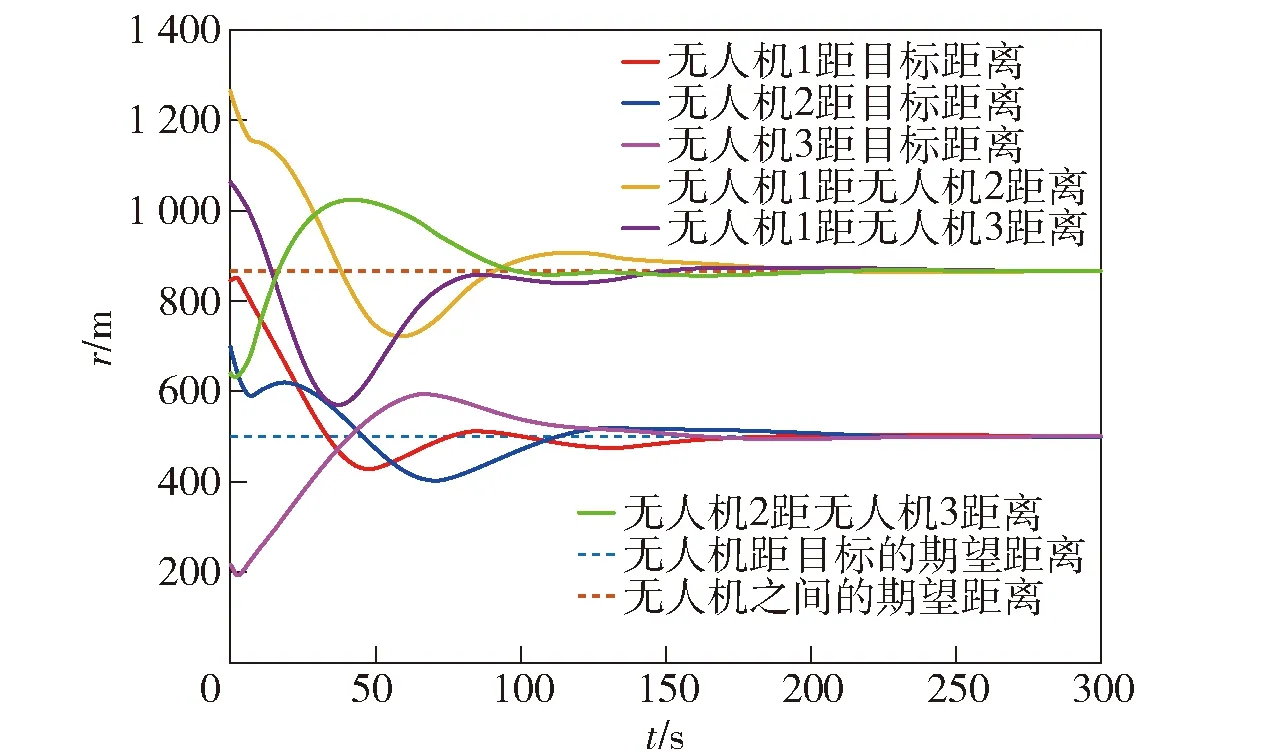
圖13 距離變化示意圖(變速目標(biāo))Fig.13 Distances among UAVs (target with variable speed)

圖14 速度變化示意圖(變速目標(biāo))Fig.14 Relative velocities of UAVs (target with variable speed)

4.4 編隊(duì)網(wǎng)絡(luò)的魯棒性

本文所提分布式協(xié)同跟蹤制導(dǎo)律較之Leader-Follower方法，最大優(yōu)勢在于提高了編隊(duì)網(wǎng)絡(luò)的魯棒性，如圖15的仿真結(jié)果所示，在3架無人機(jī)形成編隊(duì)跟蹤目標(biāo)的情況下，無人機(jī)3在t=200 s時(shí)由于不確定干擾因素脫離原有飛行軌道，飛離無人機(jī)1和無人機(jī)2的通信范圍。此種情況下，本文所提制導(dǎo)律仍然保證了無人機(jī)1和無人機(jī)2維持編隊(duì)的同時(shí)繼續(xù)定距盤旋追蹤目標(biāo)。而在t=270 s時(shí)無人機(jī)4作為補(bǔ)充的新無人機(jī)出現(xiàn)在無人機(jī)1和無人機(jī)2的通信范圍之內(nèi)時(shí)，在制導(dǎo)律的作用下3架無人機(jī)重新形成編隊(duì)定距跟蹤目標(biāo)，且無人機(jī)4的加入并未對已有的無人機(jī)1和無人機(jī)2形成的已有編隊(duì)造成顯著影響。

圖15 編隊(duì)網(wǎng)絡(luò)魯棒性示意圖Fig.15 Robustness of UAV formation

5 結(jié)論

本文提出了一種分布式多固定翼無人機(jī)協(xié)同定距盤旋跟蹤靜止及低速運(yùn)動目標(biāo)的新型制導(dǎo)方法。以相對運(yùn)動方程的極坐標(biāo)形式為基礎(chǔ)，結(jié)合反饋線性化、李雅普諾夫第2法和分布式一致性控制的基本性質(zhì)，對所提出制導(dǎo)律的穩(wěn)定性進(jìn)行了證明，并通過半實(shí)物仿真驗(yàn)證了所提制導(dǎo)方法的有效性。得到如下主要結(jié)論：

1) 根據(jù)固定翼無人機(jī)的運(yùn)動特性，基于Unicycle模型設(shè)計(jì)了多無人機(jī)協(xié)同跟蹤目標(biāo)的制導(dǎo)律，實(shí)現(xiàn)了無人機(jī)編隊(duì)對目標(biāo)的定距盤旋跟蹤，具有實(shí)際的應(yīng)用價(jià)值。

2)相比于傳統(tǒng)的Leader-Follower編隊(duì)結(jié)構(gòu)，分布式編隊(duì)結(jié)構(gòu)提高了多無人機(jī)系統(tǒng)的魯棒性，在部分無人機(jī)脫離的情況下仍然可以維持原有編隊(duì)，在新無人機(jī)加入時(shí)可以形成新的編隊(duì)。

3)搭建半實(shí)物仿真平臺，驗(yàn)證了本文提出的新型分布式多無人機(jī)協(xié)同跟蹤制導(dǎo)律可以有效跟蹤不同運(yùn)動狀態(tài)的目標(biāo)，具有實(shí)際工程應(yīng)用價(jià)值。