Belitskii約化與三階矩陣對(duì)的標(biāo)準(zhǔn)形

章 超, 蔡紅艷

(貴州大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 貴州 貴陽(yáng) 550025)

令k為代數(shù)閉域.箭圖的表示理論在眾多學(xué)科中有重要應(yīng)用,例如動(dòng)力系統(tǒng)理論.一個(gè)經(jīng)典的應(yīng)用來(lái)源于文獻(xiàn)[1].令Qi/s/o為系統(tǒng)箭圖,其中Q0:={1,2,3}以及Q1:={α:1→2,β:2→2,Γ:2→3}.Qi/s/o的一個(gè)表示(G,F,H)對(duì)應(yīng)于方程x(t+1)=Fx(t)+Gu(t),y(t)=Hx(t),其中t∈Z,x(t)∈kn,u(t)∈km且y(t)∈kp.該系統(tǒng)空間的正則點(diǎn)以及滿足特定條件的標(biāo)準(zhǔn)型得到了深入研究，見文獻(xiàn)[2-3].

從表示理論的角度來(lái)看,上述系統(tǒng)箭圖的表示理論很復(fù)雜,是最典型的野表示型代數(shù),在表示型的研究中扮演著重要的角色[4-6].由Gabriel圖化定理,代數(shù)Γ?kQ,其中Q為

,

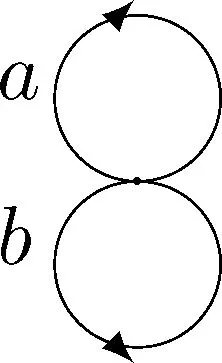
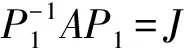
H={S∈GLn(k)|SJ=JS},

因而這個(gè)問題的研究涉及與給定矩陣可交換的矩陣問題[7].

通常來(lái)說(shuō),描述野代數(shù)的表示的同構(gòu)類是非常困難的[8-10].本文主要利用Belitskii約化算法研究代數(shù)Γ的低階表示的同構(gòu)類問題,即三階矩陣對(duì)的標(biāo)準(zhǔn)形問題.

1 Weyr標(biāo)準(zhǔn)形與Belitskii約化

研究矩陣對(duì)(A,B)的標(biāo)準(zhǔn)形,涉及與矩陣A的標(biāo)準(zhǔn)形JA可交換的矩陣問題.在研究與矩陣JA可交換矩陣問題中,矩陣的Weyr標(biāo)準(zhǔn)形比Jordan標(biāo)準(zhǔn)形更為方便.

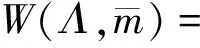
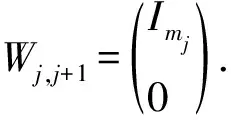
引理 1.2[12]設(shè)

J(Λ)=Jedd(Λ)⊕Jed-1d-1(Λ)⊕…Je11(Λ)

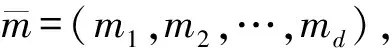
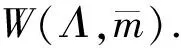
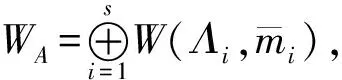
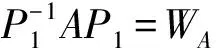
Λ={X=(Xij)d×d∈GLn(k)|Xij=0(i>j);

其中Π(Λ)為指標(biāo)集.方程組

稱之為集合Λ的定義方程組.另外,Λ也決定了集合T={1,2,…,d}上的等價(jià)關(guān)系～:i～j當(dāng)且僅當(dāng)線性方程xii-xjj=0屬于E(Λ).

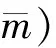
下面的引理可以直接驗(yàn)證可得.

引理 1.5如果n階方陣M=(Mij)d×d的子塊Mij是Λ-穩(wěn)定的,那么當(dāng)ij時(shí),Mij=0;否則,Mij=aijI為純量矩陣.

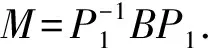
由Mlr的最小性與引理1.5可知

定義線性方程

(*)

下面對(duì)可能的3種情形進(jìn)行討論:

1) 如果方程組E(Λ)不蘊(yùn)含方程(*),則必存在X∈Λ,使得(X-1MX)lr=(M1)lr=0.

3) 如果方程組E(Λ)蘊(yùn)含方程(*),且lr,則必存在X∈Λ,使得Xrr≠Xll且方程(*)簡(jiǎn)化為其中s=rankM.

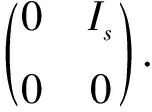
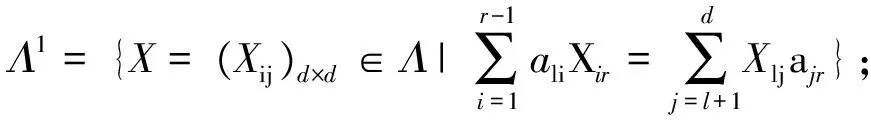
情形2Λ1={X=(Xij)d×d∈Λ|W1Xrr=XllW1};

2 三階矩陣對(duì)的相似標(biāo)準(zhǔn)形

本節(jié)將利用上節(jié)中介紹的Belitskii算法計(jì)算三階矩陣對(duì)的相似標(biāo)準(zhǔn)形,從而給出三階矩陣對(duì)的相似分類.

當(dāng)矩陣對(duì)(A,B)中A、B都為三階矩陣時(shí),以矩陣A的Weyr標(biāo)準(zhǔn)形進(jìn)行分類討論，共有以下6種情形.

情形1A相似于ΛI(xiàn)3.這種情形下,Λ=GL3(k),即所有的三階可逆矩陣構(gòu)成的集合.對(duì)于矩陣B,則存在可逆矩陣X,使得X-1BX=W1為三階Weyr標(biāo)準(zhǔn)形,所以

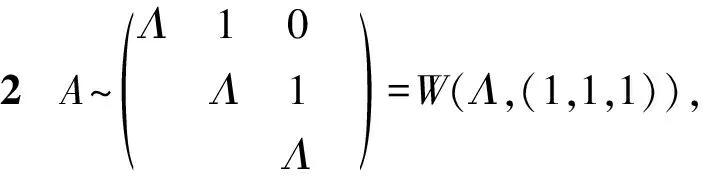
則

令矩陣

則約化過(guò)程中要滿足

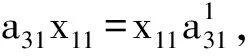
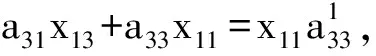
a31x13+0×x11=x11×0,

故x13=0.因此

注意到此時(shí)B3已經(jīng)Λ3-穩(wěn)定了,因此

如果a31=0,則討論過(guò)程更為復(fù)雜.記

W2=W(Λ,(1,1,1)).

類似上面的討論,利用Belitskii約化算法,按照上節(jié)中定義的序依次對(duì)變量aij逐一進(jìn)行討論,可以得到如下可能的標(biāo)準(zhǔn)形:

另外4種情形的約化方法類似,下面給出矩陣對(duì)(A,B)約化后的可能標(biāo)準(zhǔn)形.記r(b)= rank (b)為b的秩,即若b≠0,則r(b)=1;否則r(b)=0.

3 Belitskii標(biāo)準(zhǔn)形的參數(shù)數(shù)

令(M,Λ)為前面小節(jié)中的線性矩陣問題,其中M為滿足特定條件矩陣M構(gòu)成的代數(shù)簇,代數(shù)群G={S∈Λ|det(S)≠0}通過(guò)共軛作用在這些矩陣M上,矩陣M的G-軌道OM即為M的Λ-相似類,M的穩(wěn)定子群為

StabG(M)={S∈G|S-1MS=M}.

對(duì)于維數(shù),有dimG=dimOM+dimStabG(M).令ind(M)為M中的不可分解矩陣,這里的不可分解矩陣表示非準(zhǔn)對(duì)角矩陣.令

inds(M)={M∈ind(M)|dimOM=s}.

下面的定義可參見文獻(xiàn)[14].

定義 3.1ind(M)在群G作用下的參數(shù)數(shù)定義為

線性矩陣問題按照復(fù)雜度分為馴表示型與野表示型,參見文獻(xiàn)[11],粗略地說(shuō),馴表示型的線性矩陣問題(M,Λ)即為M中任意給定型號(hào)的矩陣可以由單參數(shù)量化,而野表示型矩陣問題包含了古典矩陣對(duì)的標(biāo)準(zhǔn)型問題,被認(rèn)為是沒有希望完全解決的.

定理 3.2[15]ind(M)在群G作用下的參數(shù)數(shù)μ(ind(M))為線性矩陣問題(M,Λ)的Belitskii標(biāo)準(zhǔn)形中所含參數(shù)的極大值,而且線性矩陣問題(M,Λ)為馴表示型當(dāng)且僅當(dāng)μ(ind(M))≤1.

將上述定理應(yīng)用到三階矩陣對(duì)的約化問題,結(jié)合上節(jié)計(jì)算的Belitskii標(biāo)準(zhǔn)型,可以得到下面命題.

命題 3.3設(shè)(M,Λ)為前面小節(jié)中的線性矩陣問題,則μ(ind(M))=6.特別地,(M,Λ)為野表示型的線性矩陣問題.