倒掛結構的地震作用計算分析

盧偉煌

(福建省建筑設計研究院有限公司 福建福州 350001)

1 概述

倒掛結構在實際工程中常見，現有規范或規程《高層建筑混凝土結構技術規程》[1]《建筑抗震設計規范》[2]未涉及到地震作用如何計算問題；現有整體分析計算程序計算水平地震作用，未能反映倒掛結構質量上移的特點，從而使地震作用引起的效應偏小，結構屬于不安全狀態，未能滿足建筑抗震設計規范對地震作用的要求。本文根據上述存在的問題，對各層重力荷載代表值(質量)的分布進行調整，重新計算各層水平地震作用，計算出調整前后各層水平地震作用的比值，對現有整體分析計算程序計算的各層水平地震作用進行調整，以滿足結構的實際受力狀態。

對現有的結構整體分析軟件，每層重力質量不能根據吊桿的拉力進行上移重新分布，因此，只能通過人工干預，進行每層重力質量的重分布。

2 各層重力荷載代表值(質量)的調整

根據倒掛結構的豎向構件拉力對各層重力荷載代表值(質量)的分布進行調整，如圖1所示。該示意圖表示典型的倒掛結構及倒掛結構的豎向構件的受拉狀態；現有整體分析計算程序，計算各層重力荷載代表值(質量)分布時，倒掛結構的豎向構件拉力未統計到各層重力荷載代表值(質量)中。

T1A，T2A…T6A和T1B，T2B…T6B是在“D+0.5L”工況下，每層吊桿的拉力；m1、m2、m3、m4、m5、m6、m7，是現有整體分析計算程序，計算的各層重力荷載代表值(質量)；F1、F2、F3、F4、F5、F6、F7，是現有整體分析計算程序，計算各層地震作用。

調整后各層重力荷載代表值(質量)為m01、m02、m03、m04、m05、m06、m07；

m01=m1-(T1A+T1B)

m02=m2-(T2A-T1A)-(T2B-T1B)

m03=m3-(T3A-T2A)-(T3B-T2B)

m04=m4-(T4A-T3A)-(T4B-T3B)

m05=m5-(T5A-T4A)-(T5B-T4B)

m06=m6-(T6A-T5A)-(T6B-T5B)

m07=m7+(T6A+T6B)

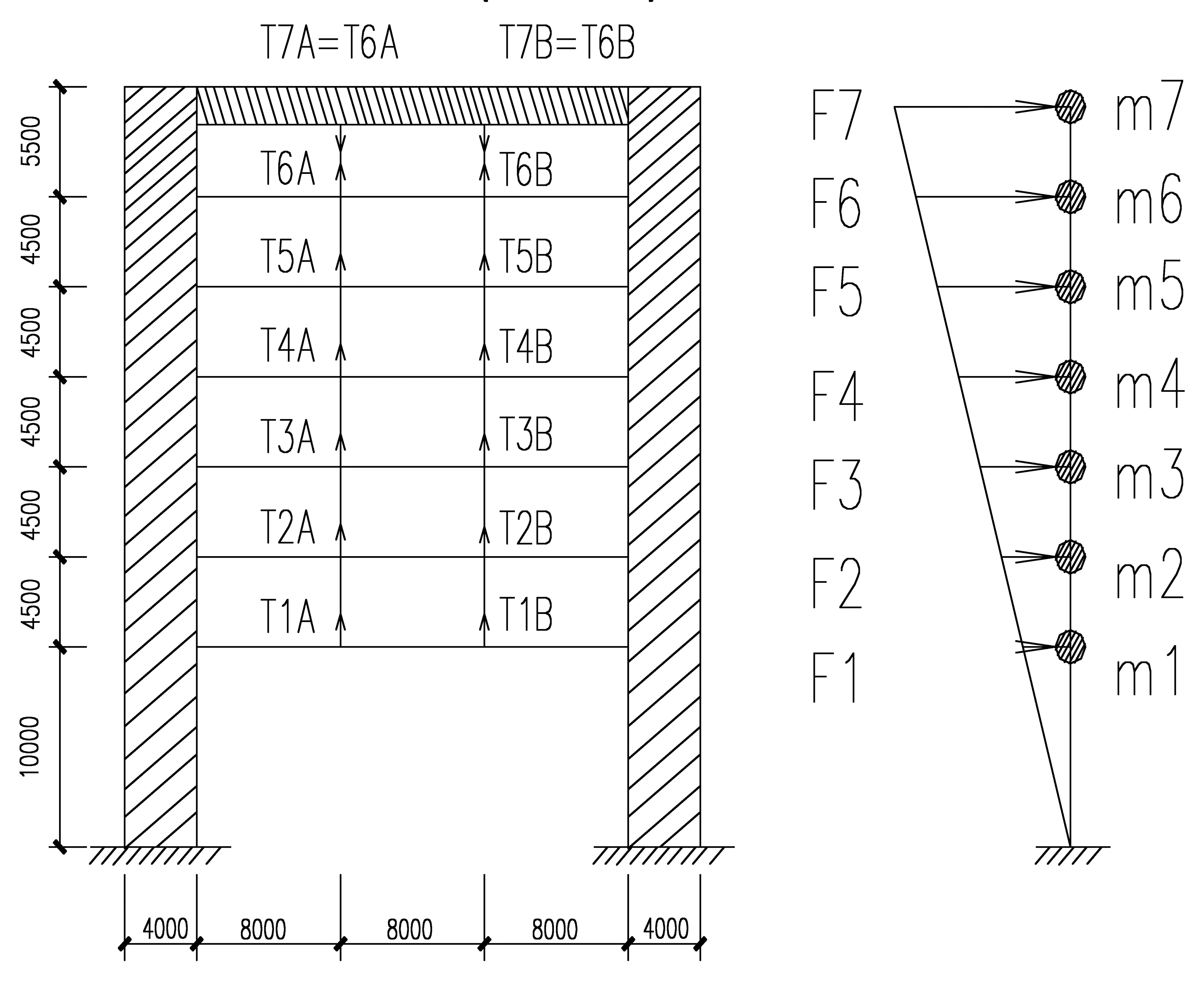
圖1 倒掛結構的示意圖

實際上現有整體分析計算程序，無法改變每層的重力荷載代表值(質量)；為了達到改變每層的重力荷載代表值(質量)目的，可以在每層的吊桿處施加向上(下)的力。

電算第1層樓面的吊桿處施加向上的力T1A、T1B；

電算第2層樓面的吊桿處施加向上的力T2A-T1A、T2B-T1B；

電算第3層樓面的吊桿處施加向上的力T3A-T2A、T3B-T2B；

電算第4層樓面的吊桿處施加向上的力T4A-T3A、T4B-T3B；

電算第5層樓面的吊桿處施加向上的力T5A-T4A、T5B-T4B；

電算第6層樓面的吊桿處施加向上的力T6A-T5A、T6B-T5B；

電算第7層樓面的吊桿處施加向下的力T6A、T6B。

3 計算調整各層重力荷載代表值(質量)后的地震作用

雖然通過各層重力荷載代表值(質量)的調整，結構的總質量不會改變，重新按現有整體分析計算程序計算各層地震作用，每層的地震作用為F01、F02、F03、F04、F05、F06、F07；計算出調整前后的各層水平地震作用的比值：K1=F01/F1，K2=F02/F2，K3=F03/F3，K4=F04/F4，K1=F05/F5，K6=F06/F6，K7=F07/F7。

用各層重力荷載代表值(質量)調整前的結構計算模型，引入各層地震作用的比值，重新計算結構內力，該計算結果即為最終的計算結果。

4 算例分析

本算例結構平面布置圖如圖2所示，剖面圖如圖3所示，地面以上7層，一層層高10m，二至六層層高4.5m，七層層高5m；屋面設置大梁，通過吊桿把下面6層的部分荷載傳到屋面大梁，屬倒掛結構；抗震設防烈度7度(0.10g)，設計地震分組第三組，建筑場地類別三類，建筑抗震設防類別丙類，結構的阻尼比5%，使用的分析程序YJK。

圖2 算例的結構各層平面布置圖

圖3 算例的結構剖面圖

按現有上部結構分析程序YJK計算結果如表1所示(由于X、Y方向完全對稱，僅列出一個方向的計算結果)。

該平面每層面積： 每層活載質量2000kN，從表1可看出，該上部結構分析程序YJK，未作上吊質量的提升。

共有44根吊柱，每根吊柱的拉力如下：二層每根吊柱拉力T2=81.1kN(40.6kN)，三層每根吊柱拉力T3=182.35kN(77.65kN)，四層每根吊柱拉力T4=290.4kN(116.7kN)，五層每根吊柱拉力T5=403.25kN(157.2kN)，六層每根吊柱拉力T6=526.8kN(201.15kN)，七層每根吊柱拉力T7=616.8kN(234.45kN)。

通過人為干預各層質量分布后，按現有上部結構分析程序YJK計算結果如表2～表6所示(由于X、Y方向完全對稱，僅列出一個方向的計算結果)。

表1 各層的質心、質量

表2 考慮扭轉藕聯時的振動周期(秒)、平動系數、扭轉系數

表3 各層的地震力Fx(kN)、各層的剪力Vx(kN)，各層地震力作用下的彎矩M(kN-M)

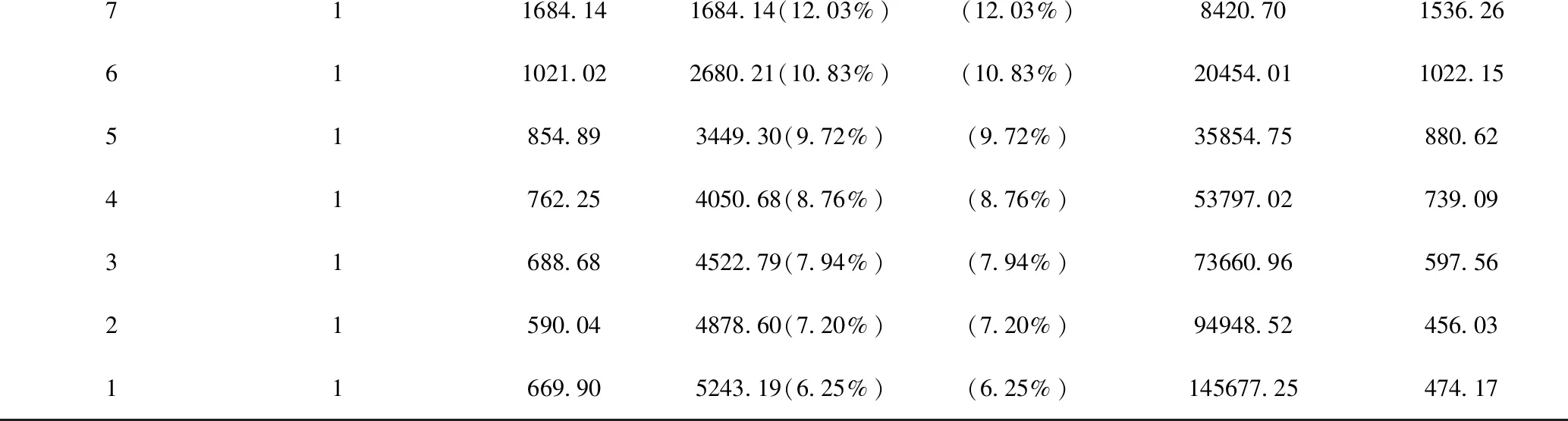
711684.141684.14(12.03%)(12.03%)8420.701536.26611021.022680.21(10.83%)(10.83%)20454.011022.1551854.893449.30(9.72%)(9.72%)35854.75880.6241762.254050.68(8.76%)(8.76%)53797.02739.0931688.684522.79(7.94%)(7.94%)73660.96597.5621590.044878.60(7.20%)(7.20%)94948.52456.0311669.905243.19(6.25%)(6.25%)145677.25474.17

表4 各層的質心、質量

表5 考慮扭轉藕聯時的振動周期(s)、平動系數、扭轉系數

表6 各層的地震力Fx(kN)、各層的剪力Vx(kN)，各層地震力作用下的彎矩M(kN-M)

通過人為干預各層質量分布后，與干預前的基底的地震剪力比5292.61/5247.35=1.008，地震做用下基底彎矩比160 545.65/145 851.41=1.1007。

每層地震力調整系數如表7所示：

表7 每層地震力調整系數

因此，把質量上移的影響，可通過每層地震力調整系數Ki來考慮。通過調整系數，對未經調整的結構整體分析模型進行各層地震作用的調整，就可以計算出基底剪力和基底彎矩。

5 結論

通過上文的算例分析，現有整體分析計算程序無法對倒掛結構按實際情況進行地震作用的分析，主要原因是目前的整體分析計算程序，統計每層重力荷載代表值(質量)時，無法減去被吊桿“吊走”的質量或增加被吊桿“下拉”的質量，造成計算地震作用錯誤。由于倒掛結構質量上移，地震作用引起的效應增大，因此對倒掛結構的工程，必須進行各層質量的調整，否則結構處于不安全狀態，不能滿足建筑抗震設計規范對地震作用的要求。

該工程算例，由于層數不多，基底剪力增加的不多，基底彎矩僅增加10%左右，但隨著層數的增加，上吊的重力質量越高，其重心也越高，基底剪力和基底彎矩也會隨著增加的更明顯。因此對這種倒掛結構地震力計算與常規結構有一定的區別。

在這里需要說明的是，對于倒掛結構的地震力計算，有一定的爭議，主要觀點是質量是不會上移，質量在那個標高，其地震作用也在那個標高。本文目的是引起科研和設計人員注意，對于倒掛結構地震力計算的問題，歡迎大家探討。