某超B級高度剪力墻結構動力彈塑性分析

郭天祥 鄭智輝

(廈門上城建筑設計有限公司 福建廈門 361012)

0 引言

鋼筋混凝土剪力墻結構整體性好，抗側剛度大，但是其基本周期短，地震慣性力較大。超B級高度剪力墻結構高度超過規范限值較多，計算要求和構造措施均應比規范規定更嚴格。另外，《高層建筑混凝土結構技術規程》[1]第5.1.13條規定，B級高度的高層建筑結構，宜采用彈塑性靜力或動力分析方法補充計算。

本文以廈門泰禾·首璽B2#樓為例，介紹超高層剪力墻結構的動力彈塑性分析。動力彈塑性分析是將地震波輸入，由結構初始狀態開始，求解每一步地震響應，并逐步積分直至地震作用結束的方法，據此結果用以考察結構在大震作用下的抗震性能是否滿足性能目標。

1 工程概況

泰禾海滄項目位于廈門海滄區，其中B2#樓建筑平面尺寸為35.0×21.3m，房屋高度172.9m(共59層)，其中上部14層為復式，層高除首層5.35m外均為2.9m，場地內設兩層地下室。主要平面及立剖面如圖1～圖3所示。

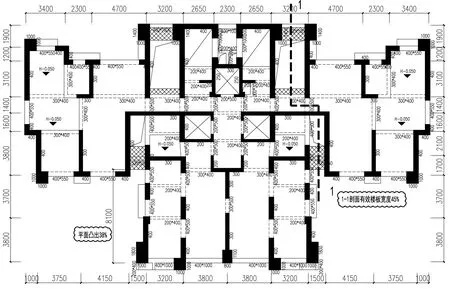
圖1 結構標準層平面圖

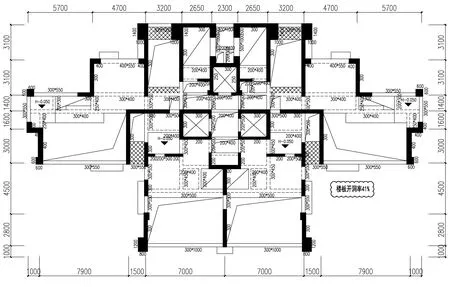
圖2 復式上層結構平面圖

圖3 立面及剖面圖

該工程設計使用年限50年，設防烈度為7度(0.15g)，地震分組第二組。基本風壓為0.8kN/m2，地面粗糙度類別為B類。

2 彈性設計分析

該工程為住宅項目，結構平面寬度較小，且隔墻較多，因此采用鋼筋混凝土剪力墻結構。高度超限、樓板不連續、平面不規則等超限情況，建筑高度超B級，高度超限是該項目的主要問題。

2.1 結構體系設計與布置

主要豎向構件布置：頂部14層為復式戶型，標準層局部柱墻到復式樓層后取消。底層墻體500mm厚，與復式樓層相關Y向墻體1～9層為400mm厚，9層以上變為300mm厚，其余Y向墻體1～9層為400mm～300mm厚，9層以上為300mm～200mm厚。X主要墻厚為300mm厚，局部樓梯間外墻為400mm厚，到上部減為300mm厚；主要剪力墻端柱為1000mm×1400mm，并在底部加強區加設型鋼。

梁系布置：外圈梁主要為550mm高，局部外圈梁(南側平面凸出部分)為1000mm高；主要的連梁及框架梁高度為500mm。

2.2 結構分析的主要設計結果

根據工程超限情況及超限論證會專家意見，結構性能目標如表1所示。另外，底部加強部位以上軸壓比大于0.25的剪力墻墻肢還應設置約束邊緣構件，中震小偏心受拉的墻肢按特一級構造，并根據拉應力情況設置型鋼。

表1 結構關鍵部位及其性能目標

彈性計算分析，主要采用YJK計算分析，并并輔以MIDAS/Building對分析結果進行校核。

小震CQC彈性分析主要計算結果表明，YJK和Building軟件計算結果比較吻合，層間位移角、自振周期、最小剪重比等各項結構總體指標均能滿足規范要求。各構件根據相應性能目標要求，按中震計算結果進行承載力設計。

3 大震動力彈塑性分析

在大震作用下，結構內力重新分布，從材料本身到整體性能均表現出非線性行為。因此，該工程采用Building建立三維結構整體模型，材料采用非線性的本構關系，進行罕遇地震作用下動力彈塑性分析，并以此考察其抗震性能。

3.1 主要技術參數指標

3.1.1模型考慮的非線性因素

在該工程的彈塑性分析過程中，考慮了以下非線性因素[2]：①材料非線性：鋼筋、混凝土及鋼材的彈塑性特性均采用材料非線性本構關系模擬，以此來表現構件的彈塑性發生、發展直到破壞的全過程；②幾何非線性：在結構變形后的幾何狀態上建立結構平衡方程，計算過程中考慮“P-Δ”效應帶來的影響。

3.1.2材料本構關系

非線性分析模型與彈性分析的模型相同，其中，對結構材料進行彈塑性本構關系的定義。

(1)基于材料的本構模型

軟件中混凝土本構關系，采用《混凝土結構設計規范》[3]附錄C中的單軸受壓應力-應變本構模型，鋼筋采用雙折線的本構模型，屈服前后剛度不同，屈服后剛度使用折減后剛度。

混凝土剪切本構采用了理想彈塑性雙折線模型，屈服前后的剛度不同，如圖4所示。

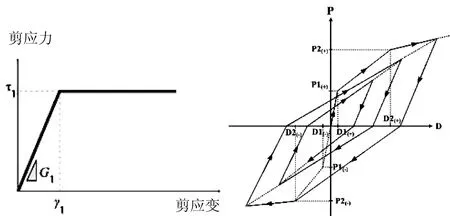
(a)理想彈塑性剪切 (b)修正武田三折線滯回模型圖4 本構模型

(2)基于截面的塑性鉸滯回模型

該工程鋼筋混凝土和型鋼混凝土構件，采用如圖4所示的修正武田三折線模型，三折線鉸輸出兩種狀態，一是開裂和開裂到屈服前狀態，二是屈服和屈服后狀態。

(3)非線性墻單元

剪力墻采用基于纖維模型的非線性剪力墻單元進行模擬。該類墻由多個墻單元構成，每個墻單元水平向和豎向被分割成一定數量的纖維，每根纖維都有一個積分點。

剪切變形計算時，綜合每個墻單元的4個高斯點位置的剪切變形。墻單元的剪切“應變等級”的定義為：墻單元剪切本構關系中單元的實際剪切應變與屈服剪應變的比值(γ/γ1)。

鋼筋的材料本構中，鋼筋的“應變等級”定義為：鋼筋實際應變與屈服應變比值(ε/ε0)。

圖中用不同顏色區分，具體如圖5所示。

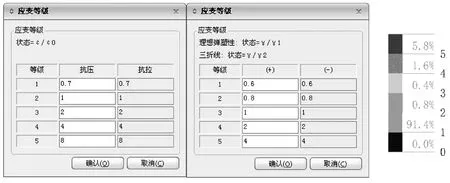
圖5 鋼筋(左)及剪力墻(右)的應變等級

3.1.3地震波的選取及輸入

該項目采用兩組天然波和一組人工波，與之作對比的是規范中的加速度反應譜，并按規范把場地特征周期加上0.05s。參照《建筑抗震設計規范》5.1.2條及條文說明的選波要求，3條地震波為：

Superstition Hills-02_NO_719，Tg(0.51)；

Superstition Hills-02_NO_724，Tg(0.52)；

ArtWave-RH2TG045，Tg(0.45)。

時程分析分兩步進行，一是施加重力荷載代表值，二是施加地震作用，輸入地震波時，峰值取310cm/s2。模型一共需輸入3組地震波記錄進行計算，每組地震波分別選取結構X、Y向作為主、次方向分別計算，主、次方向輸入地震峰值加速度按1∶0.85進行調整。結構阻尼比取0.05。

3.2 動力彈塑性分析結果

結構抗震性能評價，通過對結構整體性能(底部剪力和結構變形)和構件性能(材料損傷)兩個方面來考察。

3.2.1結構底部剪力

3條地震波在大震作用下的底部剪力約為小震作用下的3～5倍，其中，天然波2(時長18.8s)基底剪力最大。下述討論均以此條地震波Y向的結果舉例進行分析。

3.2.2結構變形

結構在地震作用主方向Y向的最大層間位移角分別為1/163、1/148、1/172，計算結果均小于規范規定的1/120限值，如圖6所示。

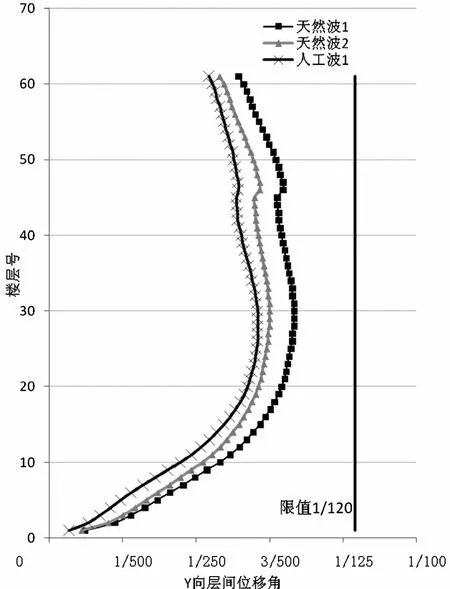
圖6 最大層間位移角

3.2.3材料損傷

本小節從構件的塑性變形與變形限值的關系來對結構進行評估，以此保證結構不因局部構件破壞而產生嚴重的破壞或倒塌。

3.2.3.1剪力墻受剪

Building中剪切破壞判斷標準，采用基于抗剪極限承載力的名義屈服應變方法：

首先，計算剪力墻構件極限抗剪承載力，此時使用的是材料強度標準值；然后，采用剪力除以墻體有效截面來計算名義屈服剪應力；最后，γ1=τ1/G，也就是屈服剪應變=屈服剪應力/剪切模量，其中G=0.4E。

Building程序設定γ1=0.00022，以此作為判斷混凝土受剪破壞的臨界點。有研究資料表明，γ1應為0.0 004～0.0 005。γ1分別取0.00 022及0.0 004進行計算表明，兩個模型層間位移角相差很小，但是剪力墻剪切破壞的結果卻變化很大，如圖7所示。因此，后續論述中，主要針對地震作用過程中剪力墻的破壞順序及程度，從概念上對計算薄弱部位采取加強措施。

(γ1=0.0002)(γ1=0.0004)圖7 不同屈服剪應變墻鉸狀態對比

為進一步了解B2#樓剪力墻在罕遇地震作用下的塑性發展情況，選取圖8所示3片剪力墻(7軸、8軸、X向)進行觀察，具體如下：

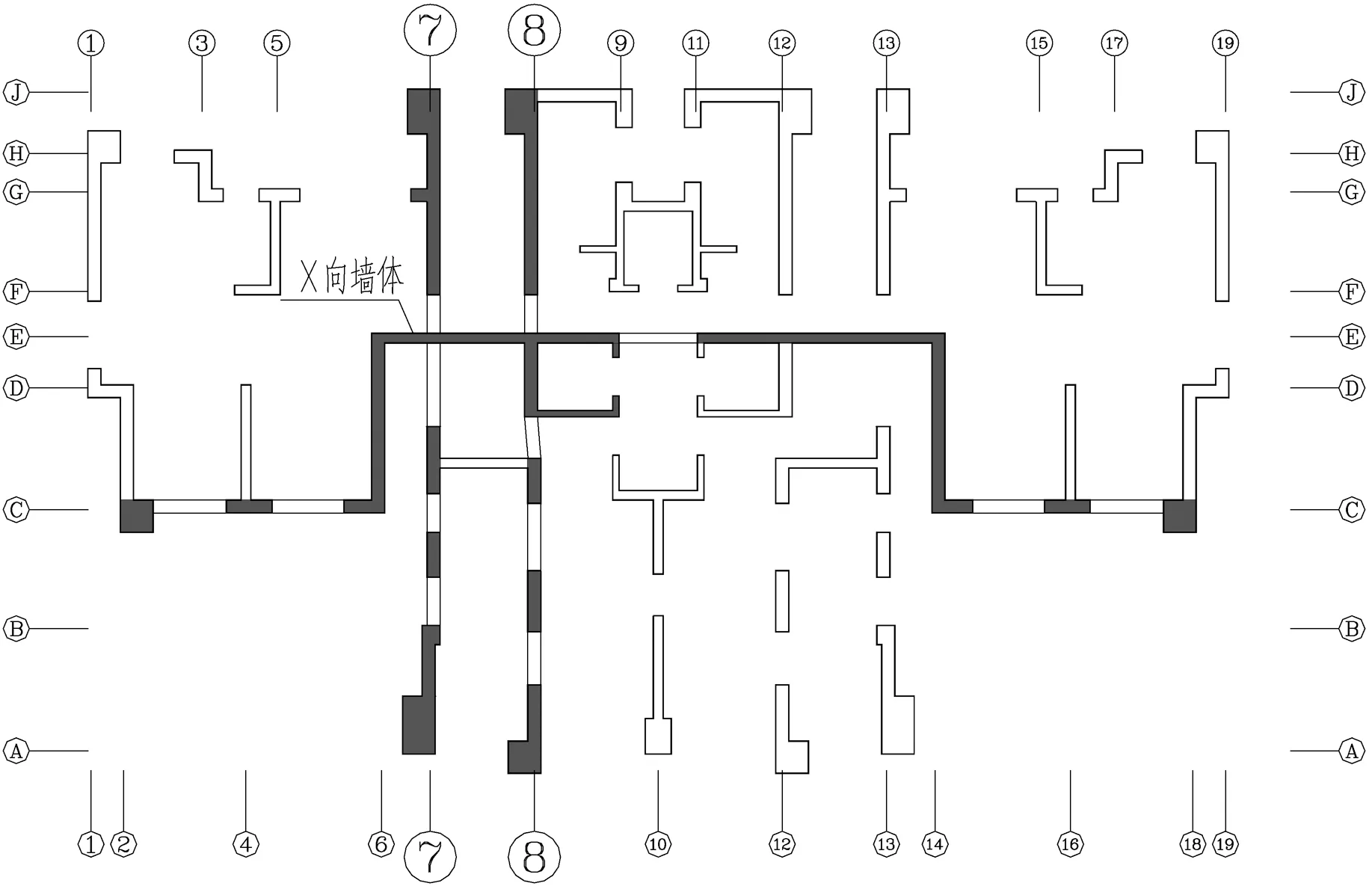
圖8 B2#樓平面示意圖

圖9所見，6.5s時7軸處剪力墻在8～16層連梁開始出現損傷，此時大部分剪力墻尚未屈服，但是豎向構件收進下層(即42～45層)位置出現塑性發展；13.5s時，J軸位置8～19層開始出現塑性損傷，豎向構件收進的下層剪力墻塑性持續發展，B軸～C軸間連梁及短肢墻塑性發展情況嚴重；到18.5s時，地震波加載結束，G軸～J軸位置在9～38層塑性發展情況嚴重，B軸～C軸間短肢墻及連梁的塑性應變等級在幾乎全高的范圍均發展至5級[4]。

(t=6.5s) (t=13.5s) (t=18.5s)圖9 7軸剪力墻混凝土剪切塑性發展過程

(t=4.5s) (t=13.5s) (t=18.5s)圖10 8軸剪力墻混凝土剪切塑性發展過程

(t=4.5s) (t=13.5s) (t=18.5s)圖11 X向剪力墻混凝土剪切塑性發展過程

圖12 部分樓層剪力墻混凝土剪切塑性發展過程注：左圖為第1、7層(型鋼變化層)，右圖為第45、46層(復式收進層)

圖10～圖11分別為8軸級X向剪力墻混凝土剪切塑性發展過程，具體情況如圖中所示。

另外，由圖12可以看出，底部加強部位(1～6層)外圈端柱設置型鋼，有效地提高了剪力墻在大震作用下的抗震能力；豎向構件收進樓層的外圈端柱，同樣有必要增設型鋼。

綜合分析以上塑性發展過程可以發現：

(1)剪力墻受剪損傷首先發生在短肢墻及連梁位置，該位置計算配筋也較大；Y向墻肢兩端設置端柱，計算配筋也較大，需設置型鋼以滿足承載力計算要求。

(2)在豎向構件收進部位的剪力墻受損情況比較嚴重，后續結構設計中應采取加強措施。

(3)X向底部墻體較Y向墻體破壞嚴重，主要原因有：結構Y向由風荷載控制，剪力墻布置較多，剪力均勻承擔；X向由地震作用控制剪力墻較少且集中，E軸處連續墻長7.6m，剛度較大；Y向墻體多已布置型鋼混凝土端柱，X向墻體未考慮性能化設計。

鑒于前述計算結果，總體而言，豎向構件的損傷較嚴重的位置主要位于以下3處：(1)剛度較大的位置。Y向長墻抗側剛度大，兩側容易出現因偏拉引起的抗剪能力削弱。(2)短肢剪力墻位置。墻肢截面較小，地震剪力作用下截面抗剪難以滿足要求。(3)豎向構件收進的位置。該位置剛度突變、受力復雜，且豎向壓重小，抗剪難以保證。

針對剪力墻損壞較明顯的部位，采取對應的加強措施后重新進行動力彈塑性分析。主要措施有：E軸處7.6m長X向剪力墻中間開洞，適當削弱剛度；提高豎向構件收進上下樓層抗震等級及配筋率；提高底部加強區豎向構件抗震等級至特一級，提高墻身豎向配筋率，并按中震正截面不屈服、斜截面彈性進行配筋；提高下部樓層短肢墻及過渡層剪力墻配筋率。

加強措施及計算結果如圖13～圖15所示。加強措施主要為：對配筋的調整，對整體計算結果影響不大。短肢墻、底部加強部位剪力墻及豎向構件收進部位等的損傷情況均得到有效改善。

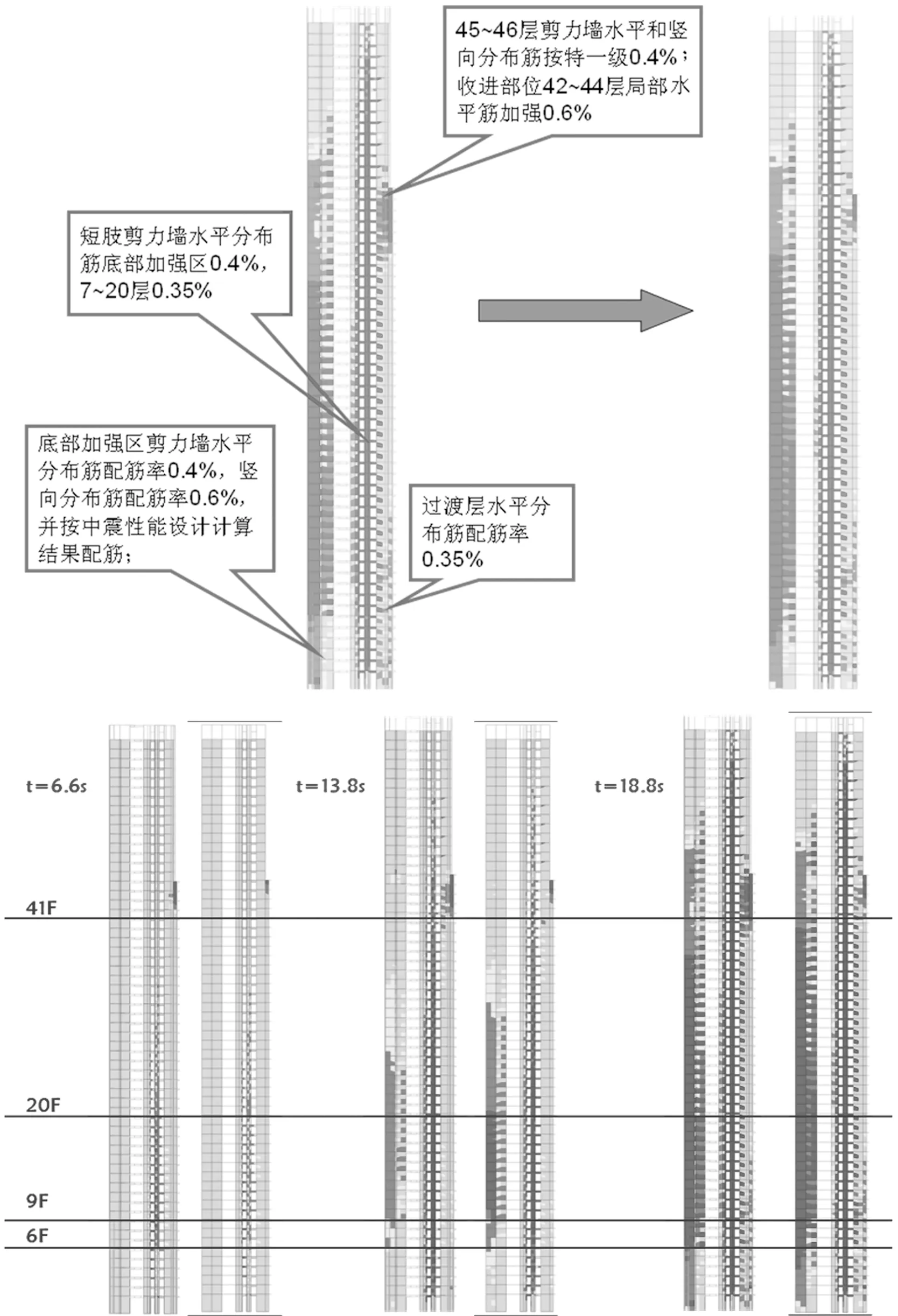
圖13 7軸剪力墻采取加強措施前(左圖)后(右圖)結果對比

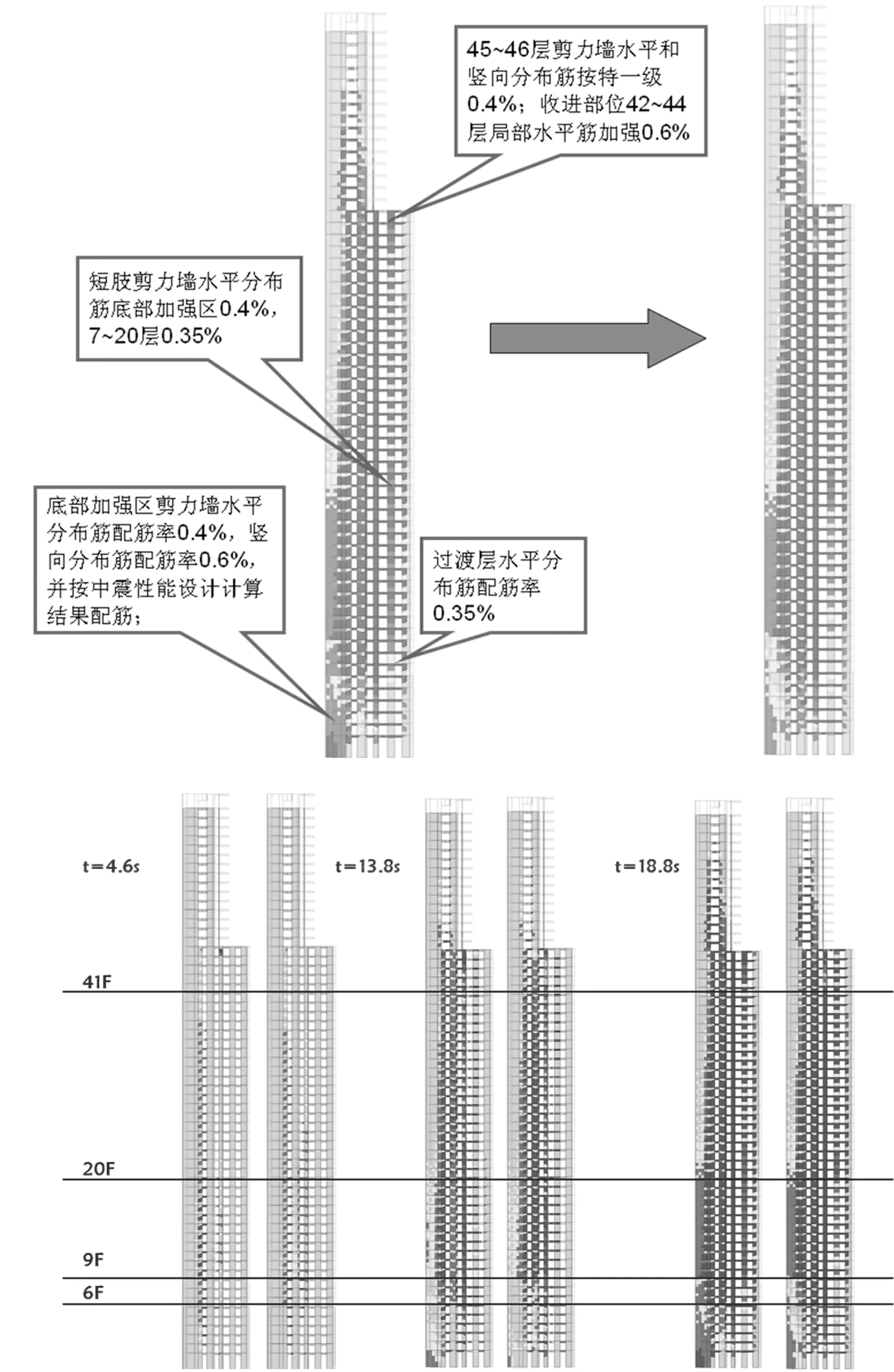
圖14 8軸剪力墻采取加強措施前(左圖)后(右圖)結果對比

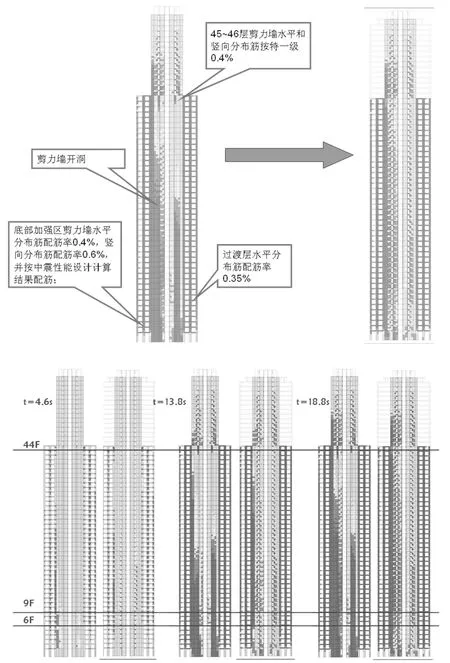
圖15 X向剪力墻采取加強措施前(左圖)后(右圖)結果對比

鑒于軟件計算參數取值對剪力墻損傷結果影響較大，為防止構件發生脆性受剪破壞，該工程控制剪力墻截面在大震下受剪滿足截面控制條件，即按《高層建筑混凝土結構技術規程》式3.11.3-4進行驗算。

驗算結果表明，剪力墻截面均滿足上述要求，部分墻肢的剪壓比驗算結果如表2所示。

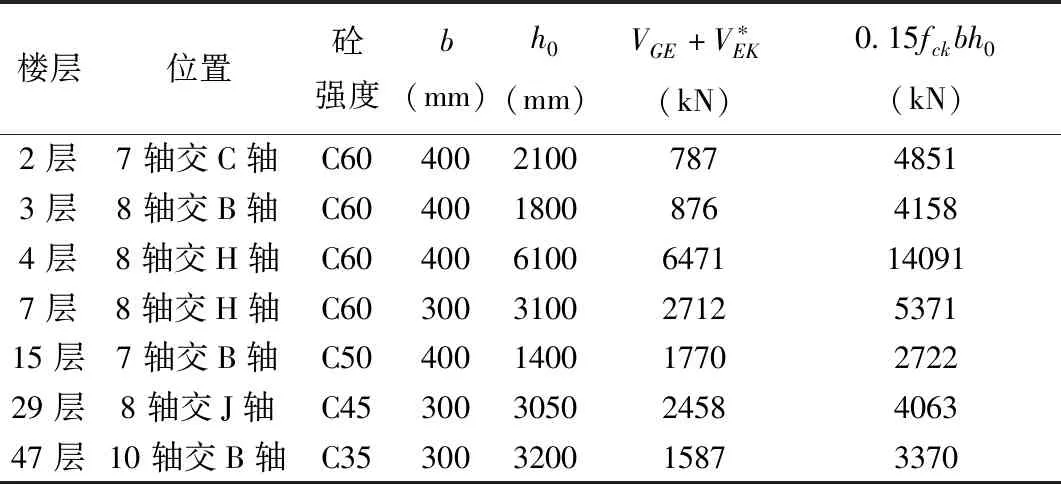
表2 墻肢剪壓比驗算

3.2.3.2剪力墻鋼筋受拉

設計對剪力墻的目標要求如下：關鍵構件→輕度損壞，普通豎向構件→部分構件中度損壞。參考文獻[5]一書中的表7-4：剪力墻損傷性能評價對應量化標準，鋼筋方面性能水平輕度損壞及中度損壞具體參考標準如下：輕度損壞：鋼筋塑性應變，γp=1～3；中度損壞：鋼筋塑性應變，γp=3～6(γp表示鋼筋塑性應變與屈服應變的比值)。

圖16為鋼筋應變等級。

圖16 鋼筋應變等級

從圖16中可以看出，鋼筋應變等級絕大部分處于1級～2級之間，即γp=0.7～1，因此剪力墻在大震下滿足性能目標要求。

4 結論

計算結果表明，目前采用的結構體系能滿足“大震不倒”的抗震性能目標。結構彈塑性發展歷程及抗震性能總結如下：

(1)輸入3組罕遇地震波進行彈塑性時程分析后可知，結構層間位移角滿足規范最低要求(1/120)且有余量。

(2)罕遇地震波持續作用下，整體結構的彈塑性發展歷程表現為：剪力墻連梁最先出現塑性鉸，隨著地震作用的進行，連梁塑性變形逐步加大，累積耗能。

(3)短肢墻及豎向構件收進的下層部位，塑性發展情況嚴重，后續結構設計中應采取加強措施。

(4)底部加強部位主要抗側力墻肢端柱采用設置型鋼的鋼骨混凝土柱，這些端柱對剪力墻能有效提高其強度、剛度以及延性性能。從計算結果上看，對剪力墻在大震作用下的抗彎、抗拉剪承載力起到明顯的有利作用。

該工程屬于超限超高層建筑，結構計算結果均滿足現行規范和規程的要求。設計時在充分計算的基礎上，采取了合理的結構布置，根據計算結果及性能化設計，對結構的薄弱部位采取有效的加強措施，并采用鋼骨混凝土構件加強剪力墻的抗彎、抗拉剪承載力，使得結構具有良好的抗震性能。