危險品道路運輸多目標路線優(yōu)化研究

李樹民 劉勇杰

摘要：根據(jù)危險品在道路運輸過程中具有運輸風險、運輸成本、運輸時間的多層屬性，提出在運輸網絡規(guī)劃中建立考慮三者因素的多目標優(yōu)化模型。將運輸風險劃分為人員風險、財產損失、環(huán)境污染損失。從監(jiān)管部門和危險品運輸企業(yè)兩者期望出發(fā)，建立運輸企業(yè)運輸費用最小、運輸風險期望值最小和運輸時間最短的多目標危險貨物道路運輸優(yōu)化模型，用層次分析法確定三項指標的權重，結合MATLAB軟件，用Dijkstra算法和集成目標函數(shù)最優(yōu)折衷路徑的擴展標號法對危險品運輸多目標優(yōu)化模型進行求解。最后通過實例分析驗證模型有效性，為監(jiān)管部門以及危險貨物運輸企業(yè)規(guī)劃運輸路線提供實際參考。

關鍵詞：危險品道路運輸;路徑優(yōu)4E;Dijkstra算法;擴展標號算法

中圖分類號：U116.2 文獻標識碼：A

0引言

隨著社會經濟的快速發(fā)展，各類危險品的道路運輸量也將逐年增加。危險物品道路運輸路線的選擇與路線周邊的人口、環(huán)境、財產安全息息相關，因此受到政府監(jiān)管部門的管制，在規(guī)劃路網時，政府部門希望危險品運輸在起訖點間總風險最小，而運輸企業(yè)更多的會考慮降低運輸成本與運輸時間，所以，找到兩者滿意的均衡路徑來保障運輸安全與運輸效益成為必要。

近年來，危險品道路運輸安全問題受到各國政府及人民群眾的高度關注，很多專家學者和科研機構對危險貨物道路運輸路網優(yōu)化問題進行了廣泛深入研究。Karkazis等人以風險和費用作為優(yōu)化目標，建立多目標路徑優(yōu)化模型，用分支定界法進行驗證求解。Jassbi等以運輸距離、風險、事故率、風險暴露人數(shù)為目標，構建多目標優(yōu)化模型，并采用遺傳算法進行了求解。Fahad A1Rukaibi等在運用GIS基礎上，引入擴散模型和碰撞模型，在不同的事故情景下分析事故的影響區(qū)域和嚴重程度，通過貨物路由算法（DGRA）確定最佳安全路線。查偉雄等建立危險貨物道路運輸阻抗函數(shù)，并根據(jù)阻抗函數(shù)，建立了路徑優(yōu)化雙層規(guī)劃模型，用模擬退火算法對模型進行了求解H。宋偉程等考慮時間和季節(jié)情況影響，建立了點危險源評價模型，在估算毒害區(qū)域面積和事故損失的基礎上，用傳統(tǒng)模型結合最大最小模型進行求解。代存杰等根據(jù)路段在路網內的地理位置，設置總風險閾值和最小相異度約束，建立了多目標優(yōu)化模型，并用遺傳算法進行求解。

本文從危險品道路運輸?shù)亩嘀貙傩猿霭l(fā)，對道路運輸網上各要素進行分析，并進行量化處理，建立危險品道路運輸多目標函數(shù)，借助Matlab軟件用Dijkstra算法和集成目標函數(shù)最優(yōu)折衷路徑的擴展標號法對危險品運輸多目標優(yōu)化模型進行求解。

1問題描述與分析

Stepl先求出和始發(fā)節(jié)點V1相連接的弧的運輸成本、運輸風險、運輸時間的最小值。由以上數(shù)據(jù)可得到：與V1連接的最小值是0.220、0.136、0.145。

Step2用Dijkstm算法分別求得運輸成本、運輸風險、運輸時間三個目標的最短路徑，分別是①-③-⑥-⑧、①-③-⑥-⑤-⑧、①-②-⑤-⑧。

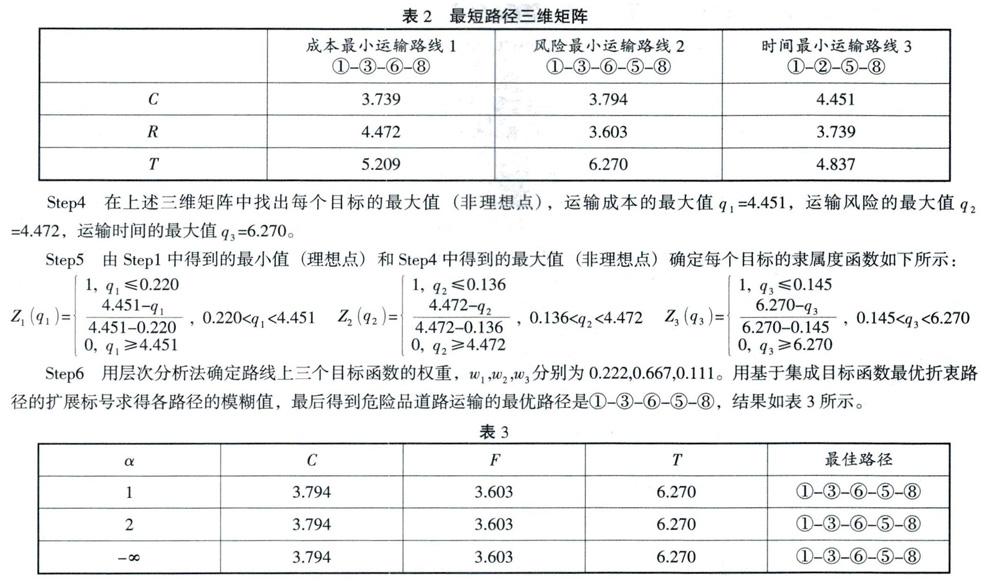
Step3計算上述每條運輸目標最短路徑的另外兩個目標值，形成的三維矩陣如表2所示：

5結論

（1）本文從運輸成本、運輸風險值、運輸時間三個運輸目標角度對危險品道路運輸路徑進行優(yōu)化分析，建立了確定環(huán)境下的道路運輸多目標決策模型，使用模糊折衷規(guī)劃算法進行求解，并應用實例來驗證了模型的有效性和可操作性。

（2）本文采用擴展標號算法求解時不需要產生所有的Pareto最優(yōu)解，只需找到一條決策者期望的Pareto最優(yōu)折衷解，大大減少了工作量。

（3）本文在構建多目標決策模型時，未考慮時間不確定、風險不確定等不確定因素影響，關于不確定環(huán)境因素下危險品道路運輸路徑決策體系和路徑優(yōu)化方法有待進一步研究。