跳頻序列的理論界
彭代淵
(1. 西南交通大學 信息科學與技術學院, 四川 成都 611756; 2. 成都工業學院 網絡空間安全研究所, 四川 成都 611730)
跳頻擴頻(FHSS)與跳時擴頻(THSS)是2種重要的擴頻通信方式.FHSS與THSS通信系統具有一系列獨特優點,例如抗干擾能力強、具有多址組網能力、抗衰落能力、易于與窄帶通信系統兼容和具有很好的保密性能等[1-2],所以,它們在民用移動通信、短距離無線通信和軍事通信等無線通信領域獲得了重要應用[3-4].在FHSS通信系統中,用跳頻序列進行頻移鍵控調制,使載波不斷地跳變.在THSS通信系統中,用跳時序列控制信號發送時刻和發送時間的長短.盡管FHSS與THSS是2個完全不同的無線通信方式,但跳頻序列和跳時序列卻具有相同的數學形式和性質.漢明(Hamming)相關函數是跳頻(時)序列的一個重要概念,跳頻序列漢明相關值的大小是影響跳頻通信系統性能的重要因素之一.設計具有優異性質的跳頻序列集一直是擴頻通信領域重要的理論研究方向.
在實際應用中,要求跳頻序列集具有理想的漢明相關特性,即全部漢明相關函數的自相關值(零時延除外)和互相關值都為零,且要求跳頻序列的數目盡可能多.但是,跳頻序列集的漢明相關值與它們的頻隙數目、序列長度和序列數目等參數有關,這些參數之間的數學關系稱為“跳頻序列的理論界”.跳頻序列理論界是跳頻序列集性能優異的評價標準,對跳頻序列設計具有重要的指導意義.早期跳頻序列的理論界基本上是在某些特殊條件下建立的.Lempel等[5]在1974年首先建立了“序列數目為1或2時,周期漢明相關函數的理論界”.1982年,Seay[6]給出了“限定漢明相關條件下序列數目和序列長度的理論界”.梅文華[7]在1992年建立了“非重復跳頻序列集的理論界”,1994年建立了“寬間隔的非重復跳頻序列集的理論界”[8].2004年,Peng等[9]建立了“一般跳頻序列集的理論界”,該理論界被稱為Peng-Fan界,作為判定一般跳頻序列集性能的標準[10-12].2009年,Ding等[13]利用糾錯碼的理論界得到了幾個新的跳頻序列集的理論界.2011年,利用糾錯碼中的Singleton界,得出了跳頻序列集的1個最大非平凡漢明相關的新理論界[14].
這些理論界幾乎都是針對周期漢明相關函數的.但是,在實際應用中,跳頻序列的部分漢明相關函數能更好地描述跳頻擴頻通信系統的性能[15].由于研究跳頻序列的部分漢明相關函數很難,所以相關研究成果較少.在2004年,Eun等[15]導出了1個序列的部分漢明自相關函數的理論界(Eun-Jin-Hong-Song界).近年來,我們開始致力于研究跳頻序列的部分漢明相關函數特性及其理論界,已獲得一些新的結果.2010年,我們建立了任意跳頻序列集的部分漢明相關函數的理論界,Eun-Jin-Hong-Song界是這個結果的特殊情況[16].
在上述理論界中,討論的是跳頻序列集漢明相關函數的最大值滿足的不等式,這類理論界被稱之為“最大漢明相關的理論界”.近年來,我們開始研究跳頻序列平均漢明相關的性質及其理論界.在2010年,首次建立了滿足跳頻序列集的頻隙數目、序列長度、序列數目、平均漢明自相關值和平均漢明互相關值等參數的理論界[17],同時建立平均周期部分漢明相關的理論界,得到了滿足跳頻序列集的頻隙數目、相關窗長度、序列數目、平均周期部分漢明自相關值和平均周期部分漢明互相關值等參數的不等式[18].
本文全面系統地闡述跳頻擴頻序列集的理論界.
1 跳頻序列周期漢明相關函數的理論界
跳頻序列的漢明相關函數是刻劃跳頻通信系統性能的重要參數.首先給出一些符號和跳頻序列及其漢明相關函數的定義.
用F={f1,f2,…,fq}表示頻隙集,q=|F| 表示頻隙數目,x=(x0,x1,…,xN-1) (xi∈F,i=0,1,…,N-1)稱為F上的1個跳頻序列,N稱為跳頻序列x的長度或周期,S是M個長度為N的跳頻序列組成的集合.
對于任給2個頻隙f1,f2∈F,令
定義 1.1任給2個跳頻序列x=(x0,x1,…,xN-1),y=(y0,y1,…,yN-1)∈S,l為整數,0≤l l=0,1,…,N-1 (1) 稱為跳頻序列x和y關于時延l的周期漢明相關函數,其中下標加法i+l按模N運算,這里只考慮正時延l.對于已知的跳頻序列集S,其最大周期漢明自相關邊峰值Ha(S) 及最大周期漢明互相關值Hc(S)分別定義為: Ha(S)=man{H(x,x;l)|x∈S, l=1,2,…,N-1}; Hc(S)=max{H(x,y;l)|x,y∈S, x≠y,l=0,1,…,N-1}. 令Hm(S)=max{Ha(S),Hc(S)}.在不引起混淆的時候,令Ha=Ha(S),Hc=Hc(S),Hm=Hm(S). 1個跳頻序列集S包含以下參數:頻隙數目q、序列長度N、序列數目M、最大漢明自相關邊峰值Ha與最大漢明互相關值Hc.根據跳頻通信設計的要求,應該使跳頻序列集的參數具有如下特性[19-20]: 1) 最大漢明自相關邊峰值Ha盡可能小; 2) 最大漢明互相關值Hc盡可能小; 3) 當參數Ha、Hc、q及N給定時,序列數目M盡可能大. 但是,上述參數受到一些約束條件的限制.為了評估跳頻序列的性能,必須找出這些參數之間的數學關系式,這就是跳頻序列理論界的研究內容.早在1974年,對于由1個或2個序列組成的特殊序列集,Lempel等[5]給出了周期漢明相關函數的理論界. 設u≥0,v>0是2個整數,用q(u,v)表示u除以v的商,用r(u,v)表示u除以v所得的余數. 定理 1.1[5](Lempel-Greenberger界) 設S是由F上的1個長度為N的跳頻序列組成的集合,r=r(N,q),那么 H (2) 推論 1.2[5](Lempel-Greenberger界) 設S是由F上的1個長度為N的序列組成的集合,如果N=pn-1,q=pk,其中p是1個給定的素數,k和n是任意2個整數,滿足1≤k Ha≥pn-k-1. (3) 定理 1.3[5](Lempel-Greenberger界) 設S是由F上的2個長度為N的跳頻序列組成的集合,如果N=pn-1≥2,q=pk,其中p是1個給定的素數,k和n是任意2個整數,滿足1≤k Hm≥pn-k. (4) 如果跳頻序列集S中的任意2個不同序列的參數使得(4)式的等號成立,則稱S是1個Lempel-Greenberger最優跳頻序列集. 1982年,Seay[6]給出了如下跳頻序列集周期漢明相關函數的理論界. 定理1.4[6](Seay界) 設S是由F上M個長度為N的跳頻序列組成的集合,如果M=qk+1,其中k是S內任意2個序列間的最大漢明相關值,那么 (5) Lempel-Greenberger界和Seay界存在如下局限性: 1) 只考慮了周期漢明相關函數的理論界,沒有研究非周期漢明相關函數的理論界; 2) 即使對于周期漢明相關函數,也只考慮了M的一些特殊值,例如M=1,2或qk+1,而不是對任意的M; 3) 沒有區分最大漢明自相關邊峰值Ha和最大漢明互相關值Hc,而僅討論了最大非平凡漢明相關值Hm的下界. 由于實際跳頻通信系統使用序列的數目都大于2,并且跳頻序列集的漢明自相關值和漢明互相關值是相互聯系的,即如果最大漢明自相關邊峰值小,則它的最大漢明互相關值往往就大,反之亦然.所以根據Lempel-Greenberger 界與Seay界判定跳頻通信系統的性能具有極大的局限性.研究跳頻序列集一般參數滿足的理論界具有重要的理論意義與應用價值. 2004年,文獻[9]找到了跳頻序列集任意參數滿足的數學關系式,建立了跳頻序列集最大周期漢明自相關邊峰值和最大周期漢明互相關值的下界定理. 對于實數x,用x表示小于或等于x的最大整數,用x表示大于或等于x的最小整數. 定理 1.5[9](Peng-Fan界) 設S是由F上M個長度為N的跳頻序列組成的集合,q=|F|,令I=MN/q,則有 (N-1)qHa+(M-1)NqHc≥ (MN-q)N, (6) (N-1)MHa+(M-1)MNHc≥ 2IMN-(I+1)Iq. (7) 如果跳頻序列集S的參數(Ha,Hc)是不等式(6)(或(7))的最小整數解,則稱(Ha,Hc)是S的1個最優周期漢明相關對,同時稱S是1個最優周期跳頻序列集. 注意到Hm=max{Ha,Hc},可得如下推論. 推論 1.6設S是由F上M個長度為N的跳頻序列組成的集合,q=|F|,令I=MN/q,則有 H (8) H (9) 2016年,Chen等[21]證明了理論界(8)與(9)式是等價的. 如果M=1,那么N=Iq+r,0≤r 推論 1.7設S是由F上1個長度為N的跳頻序列組成的集合,q=|F|,則有 H (10) (10)式即是Lempel-Greenberger界(2). 推論 1.8設S是由F上M個長度為N的跳頻序列組成的集合,q=|F|.如果存在素數p和正整數k、n滿足0≤k (pn-2)Ha+(M-1)(pn-1)Hc≥ Mp2n-k-2Mpn-k-pn+2, (11) H (12) 容易看到,Lempel-Greenberger界(3)是界(12)在M=1時的特殊情況,Lempel-Greenberger界(4)是界(12)當M=2時的特殊情況. 推論 1.9設S是由F上M個長度為N的跳頻序列組成的集合,q=|F|,令k=Hc,如果M=qk+1,那么 (13) 推論 1.10設S是由F上M個長度為N的跳頻序列組成的集合,q=|F|,令k=Hm,如果M=qk+1,那么 (14) 因為不等式 對任意正整數k成立,所以在推論1.10的條件下,界(14)比Seay界(5)更緊. 定理 1.5被學術界稱為Peng-Fan界.Peng-Fan界打破了跳頻序列理論界研究多年停滯不前的狀況,引起了國內外許多學者對跳頻序列理論界的研究興趣,從此以后,一批新的理論界不斷被發表出來. 2009年,Ding等[13]利用循環碼的Singleton界,給出了跳頻序列集的1個新的理論上界. 定理 1.11[13](Ding界) 令F是1個大小為q的頻隙集,S是1個在頻隙集F上的M個具有序列長度N的跳頻序列組成的集合,Hm是序列集S的最大周期漢明相關值,則有 (15) 2011年,Yang等[14]利用循環碼的Singleton界,給出了跳頻序列集最大周期漢明相關值的1個新下界. 定理 1.12[14](Yang界) 令F是1個大小為q的頻隙集,S是1個在頻隙集F上的M個具有序列長度N的跳頻序列組成的集合,Hm是序列集S的最大漢明相關值,則有 Hm≥logqMN-1. (16) 在2013年,Liu和Peng[ 22]改進了跳頻序列集的Singleton界. 定理1.13[22](Liu-Peng界) 令F是1個大小為q的頻隙集,S是1個在頻隙集F上的M個具有序列長度N的跳頻序列組成的集合,則有 在2014年,Liu等[ 23]通過引入M?bius函數,進一步改進了跳頻序列集的Singleton界. 定理 1.14[23](Liu-Peng-Han界) 令F是1個大小為q的頻隙集,S是1個在頻隙集F上的M個具有序列長度N的跳頻序列組成的集合,則有 (18) 其中μ(d)是M?bius函數,定義為 跳頻序列的非周期漢明相關函數是刻劃跳頻通信系統頻率重合的又一個重要指標.首先給出跳頻序列非周期漢明相關函數的定義. 定義 2.1對于任意2個長度為N的跳頻序列x=(x0,x1,…,xN-1),y=(y0,y1,…,yN-1)∈S,l為整數,且0≤l l=0,1,…,N-1. (19) l=1,2,…,N-1}; (20) x≠y,l=0,1,…,N-1}. (21) 研究跳頻序列非周期漢明相關函數的理論界較難,因此很長時間未見有關研究結果.在2004年,我們首次給出了跳頻序列集最大非周期漢明自相關邊峰值和最大非周期漢明互相關值的理論界[ 9]. 定理 2.1[9](Peng-Fan界) 設S是由F上M個長度為N的跳頻序列組成的集合,q=|F|,J=2MN/(M+q),則有 (3MN-qN-M-q)N, (22) (4J-N-1)MN-J(J+1)(M+q). (23) 推論 2.2設S是由F上M個長度為N的跳頻序列組成的集合,那么 (24) (25) 2013年,Liu等[ 24]改進了跳頻序列集非周期漢明相關函數的理論界. 定理 2.3[24](Liu-Peng-Niu界) 令F是1個大小為q的頻隙集,S是1個在頻隙集F上的M個具有序列長度N的跳頻序列組成的集合,則有 MN2-qN, (26) 2IMN-(I+1)Iq, (27) 其中I為MN/q的整數部分. 2014年,Liu和Peng[ 25]建立了一個新的關于非周期漢明相關的跳頻序列集序列數目的理論上界. (28) 從理論上講,跳頻擴頻通信系統使用的跳頻序列集應具有“理想”的相關特性,即全部自相關值(零時延除外)和全部互相關值都為零.可是,從跳頻序列理論界可知,這樣的跳頻序列集必須滿足 MN=q, 其中,N為序列周期(長度),M為序列個數,q為頻隙數目.對于實際跳頻擴頻通信系統,由于序列長度遠遠大于頻隙數目,所以關系MN=q不可能成立.這就是說:“理想”跳頻序列集是不存在的!因此,在實際跳頻擴頻通信系統中,總是存在用戶間的多址干擾. 跳頻序列理論界同時說明,跳頻序列集的序列個數隨著漢明相關值的降低而減少.可見,實際跳頻擴頻通信系統需要“跳頻序列多、漢明相關值小”的跳頻序列集,是不能實現的. 出現以上問題的主要原因是:為了便于進行理論研究,人們往往在序列的全周期內考慮漢明相關函數.為了克服以上困難,應該在“較小”的時延范圍內考慮序列的漢明相關性.跳頻序列的部分漢明相關就是在1個小于序列周期的相關窗內定義序列的漢明相關函數.由于跳頻系統中的同步時間有限以及硬件的復雜性,通常跳頻序列的相關窗的長度遠遠小于所選序列的周期,而且相關窗的長度會隨著信道條件的變化而改變,所以部分漢明相關比全周期漢明相關能更好地衡量系統的性能.盡管對跳頻序列部分漢明相關的研究較早,但遺憾的是,由于研究的困難性,公開的研究結果并不多. 近年我們對跳頻序列部分漢明相關函數進行了持續研究,獲得了一系列成果.首先給出跳頻序列部分漢明相關函數的定義. 定義 3.1對于任意2個跳頻序列x=(x0,x1,…,xN-1),y=(y0,y1,…,yN-1)∈S,序列x和y在相對時延為,相關窗起點為j,相關窗長度為L時的周期部分漢明相關函數定義為: 0 (29) 其中,下標i+按模N運算.當x=y時,H(x,y;j|L;τ)稱為周期部分漢明自相關函數;當x≠y時稱為周期部分漢明互相關函數.如果j=0 并且L=N,周期部分漢明相關函數與周期漢明相關函數一致. 跳頻序列集S的最大周期部分漢明自相關Pa(L)、最大周期部分漢明互相關Pc(L)和最大周期部分漢明相關Pm(L)分別定義為: Pa(L)= 0<τ (30) Pc(L)= x≠y,0≤τ,j (31) Pm(L)=max{Pa(L),Pc(L)}. (32) 類似地,可以定義跳頻序列的非周期部分漢明相關函數. 定義 3.2對于任意2個跳頻序列x=(x0,x1,…,xN-1),y=(y0,y1,…,yN-1)∈S,序列x和y在相對時延為,相關窗起點為j,相關窗長度為L時的非周期部分漢明相關函數定義為: 其中,下標i+按模N運算.當x=y時,稱為非周期部分漢明自相關函數;當x≠y時稱為非周期部分漢明互相關函數.如果j=0 并且L=N,(33)式即表示(19)式中定義的非周期漢明相關函數. 0<τ (34) x≠y,0≤τ (35) (36) 由于跳頻序列的部分漢明相關函數比較復雜,相關理論界的研究結果較少.在2004年,Eun 等[15]推導了1個跳頻序列的周期部分漢明自相關的理論界. 定理 3.1[15](Eun界) 令F是1個大小為q的頻隙集,對于F上序列長度為N,相關窗長度為L的跳頻序列,有 P (37) 其中,r是N模q的最小非負剩余. 由于實際跳頻通信系統使用序列的數目都大于1,根據Eun等理論界來判定跳頻通信系統的性能具有如下局限性: 1) 只考慮了周期部分漢明相關函數的理論界,沒有研究非周期部分漢明相關函數的理論界; 2) 即使對于最大周期部分漢明相關函數,也只考慮了1個序列最大周期部分漢明自相關值; 3) 沒有區分最大部分漢明自相關和最大部分漢明互相關. 2010年,Niu等[16]建立了跳頻序列集周期部分漢明相關函數一般形式的理論界. 定理 3.2[16](Niu-Peng界) 令F是1個大小為q的頻隙集,S為F上M個長度為N的跳頻序列構成的集合,相關窗長度為L(L≤N),則有: q(N-1)Pa+q(M-1)NPc≥ LMN-Lq; (38) MN(N-1)Pa+M(M-1)N2Pc≥ [2MN-(I+1)q]LI, (39) 其中I=NM/q. 因為Pm=max{Pa,Pc},由定理3.2直接導出以下結果. 定理 3.3[16](Niu-Peng界) 令F是1個大小為q的頻隙集,S為F上M個長度為N的跳頻序列構成的集合,相關窗長度為L(L≤N),則有 P (40) P (41) 由于Pm是正整數,所以,不等式(40)與(41)可以分別寫成: P (42) P (43) 2014年,Cai等[26]改進了該理論界. 定理 3.4[26](Cai界) 令F是1個大小為q的頻隙集,S為F上M個長度為N的跳頻序列構成的集合,相關窗長度為L(L≤N),則有 P (44) P (45) 2016年,我們找到了上述幾個理論界之間的等價性[27]. 定理 3.5[27](Wang-Peng界) 令F是1個大小為q的頻隙集,S為F上M個長度為N的跳頻序列構成的集合,相關窗長度為L(L≤N),則有: 1) 理論界(44)與理論界(45)是等價的,即 P 2) 關于理論界(42)與理論界(43)的等價性,有以下結論:設MN>q,L=sq+r,s≥0,0≤r≤q-1. ① 如果L>q,q不整除MN,且 那么 P ② 否則,理論界(42)與理論界(43)是等價的,亦即 P 在定理3.2或定理3.3中令序列個數M=1,得到如下結果. 定理 3.6(Niu-Peng界) 令F是1個大小為q的頻隙集,S為F上的1個長度為N的跳頻序列構成的集合,相關窗長度為L(L≤N),則有: P (46) P (47) 其中I=N/q. 注意到,N=qI+r,容易把(47)式化成(37)式,所以,Eun界是定理3.4的直接推論. 在早期跳頻序列理論界研究中,幾乎都是討論跳頻序列集漢明相關函數的最大值,使用最大漢明自相關邊峰值和最大漢明互相關值來評價跳頻序列集的性能,這是從“最壞”的角度來評價跳頻通信系統性能,主要原因是數學處理的容易性.這類理論界被稱之為“最大漢明相關理論界”.而對于跳頻擴頻通信系統性能評估,漢明相關函數的平均值更符合實際.由于研究漢明相關平均值很難,所以,關于平均漢明相關理論界的研究結果不多.近年來,我們深入討論了漢明相關平均值的性質,開始研究平均漢明相關的理論界,建立了一批理論界. 首先給出跳頻序列集平均周期漢明自相關和平均周期漢明互相關的定義. 定義 4.1令S是F上的由M個長度為N的跳頻序列組成的集合,那么 S (48) S (49) 分別稱為跳頻序列集S的周期漢明自相關碰撞總數和周期漢明互相關碰撞總數.將 A (50) A (51) 分別稱為序列集S的平均周期漢明自相關和平均周期漢明互相關. 在不引起混淆的時候,令Sa=Sa(S),Sc=Sc(S),Aa=Aa(S),Ac=Ac(S). 很明顯,跳頻序列集的平均碰撞數能夠度量跳時通信系統的平均錯誤性能.希望Aa(S)和Ac(S)越小越好. 2010年,首次建立了跳頻序列集的頻隙數目、序列長度、序列數目、平均漢明自相關值和平均漢明互相關值等參數滿足的理論界[17-18]. 定理 4.1[17](Peng-Niu-Tang界) 令S是頻隙大小為q的集合F上的由M個長度為N的跳頻序列組成的集合.設Aa和Ac分別表示序列集S的平均周期漢明自相關和平均周期漢明互相關,則有 (52) 如果1個跳頻序列集S的參數使得(52)式的等號成立,則稱S是關于平均周期漢明相關最優的跳頻序列集. 以下定理找到了最大周期漢明相關最優的跳頻序列集與平均周期漢明相關最優的跳頻序列集之間的1個關系. 定理 4.2[17](Peng-Niu-Tang界) 令S是由F上M個長度為N的跳頻序列組成的集合.如果S是關于最大周期漢明相關最優的跳頻序列集,那么S同時也是關于平均周期漢明相關最優的跳頻序列集. 一般地說,定理4.2的逆不成立,即“關于平均周期漢明相關最優的跳頻序列集”不一定是“關于最大周期漢明相關最優的跳頻序列集”.現在用一個例子進行說明. 例 4.1設頻隙集F={0,1,2,3,4,5,6},構造3次跳頻序列集S[17]如下: 即 S={s(1)=(0,1,1,6,1,6,6), s(2)=(0,2,2,5,2,5,5), s(3)=(0,3,3,4,3,4,4), s(4)=(0,4,4,3,4,3,3), s(5)=(0,5,5,2,5,2,2), s(6)=(0,6,6,1,6,1,1) }. 可見,跳頻序列集S具有以下參數:頻隙數目q=7,序列長度N=7,序列數目M=6.S的周期漢明相關值為 H(s(i),s(j);τ)= 可以驗證,這些參數使(52)式的左右兩邊相等,所以S是“關于平均周期漢明相關最優的跳頻序列集”.將這些參數代入(6)式,得到819>245,所以S不是“關于最大周期漢明相關最優的跳頻序列集”. 現在討論跳頻序列集部分漢明相關函數平均值的理論界.首先給出部分漢明相關函數平均值的定義. 定義 4.2[18]令F是1個大小為q的頻隙集,S為F上M個長度為N的跳頻序列構成的集合,相關窗長度為L(L≤N).跳頻序列集S在相關窗L內的周期部分漢明自相關函數總值與周期部分漢明互相關總值分別定義為: T (53) Tc(L):= (54) 跳頻序列集S在相關窗L內的周期部分漢明自相關函數平均值與周期部分漢明互相關平均值分別定義為: A (55) A (56) 2010年,我們建立平均周期部分漢明相關的理論界,得到了跳頻序列集的頻隙數目、相關窗長度、序列數目、平均周期部分漢明自相關值和平均周期部分漢明互相關值等參數滿足的不等式[18]. 定理 4.3[18](Niu-Peng-Liu界) 令F是1個大小為q的頻隙集,S為F上M個長度為N的跳頻序列構成的集合,相關窗長度為L(L≤N),則有 (57) (58) 其中I=NM/q. 在(57)式中,令L=N,則(57)式成為(52)式.所以,Peng-Niu-Tang界(52)是Niu-Peng-Liu界(57)的特殊情況. 2015年,我們通過分析每個頻隙在整個序列集中的分布特性,改進了跳頻序列集平均部分漢明相關函數理論界. 定理 4.4[28](Zhou-Peng界) 令F是1個大小為q的頻隙集,S為F上M個長度為N的跳頻序列構成的集合,相關窗長度為L(L≤N),則有 (59) 其中r是NM模q的最小非負剩余. 由于(58)式中的I與(59)式中的r具有關系NM=Iq+r(0≤r (2MN-Iq-q)LI= (MN+r-q)(MN-r)L/q= (M2N2+qr-r2-qMN)L/q, 所以,理論界(58)與(59)式是等價的. 跳頻序列漢明相關值的大小是決定跳頻擴頻通信系統性能的重要因素之一,跳頻序列理論界是跳頻序列性能優異的評價標準,一直是擴頻通信理論的核心研究課題.有關跳頻序列理論界的研究成果最早于1974年公開發表,之后很少報道.直到2004年,我們找到了跳頻序列集任意參數滿足的數學關系式,分別建立了跳頻序列集周期漢明相關函數的理論界與非周期漢明相關函數的理論界.從此開始,在國內外掀起了跳頻序列理論界的研究熱潮,許多學者開始從事跳頻序列理論界的研究.據不完全統計,國家自然科學基金資助的有關跳頻序列的研究項目不低于10項.研究成果非常豐富,研究范圍不斷擴大.從研究跳頻序列周期漢明相關函數的理論界開始,逐步擴展到研究跳頻序列非周期漢明相關函數的理論界和跳頻序列部分漢明相關函數的理論界,不但研究跳頻序列漢明相關函數最大值的理論界,而且研究跳頻序列漢明相關函數平均值的理論界.并且提出了“低碰撞區跳頻序列”的概念,為跳頻序列的研究開創了一個新方向.本文完整地系統地闡述了跳頻序列理論界的研究成果.關于低碰撞區跳頻序列的理論界,將另外撰文論述.2 跳頻序列非周期漢明相關函數的理論界
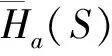
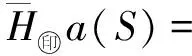


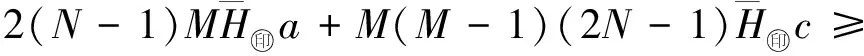

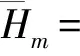

3 跳頻序列部分漢明相關函數的理論界

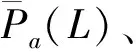
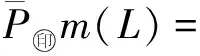
4 跳頻序列漢明相關函數平均值的理論界

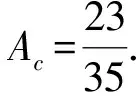
5 結論

