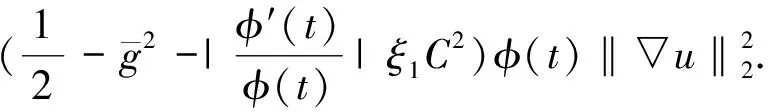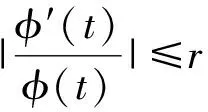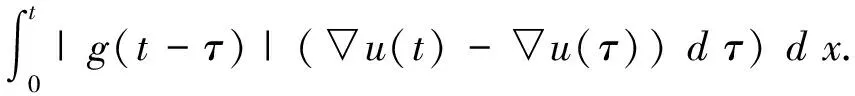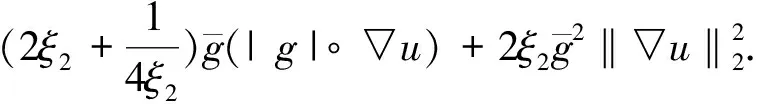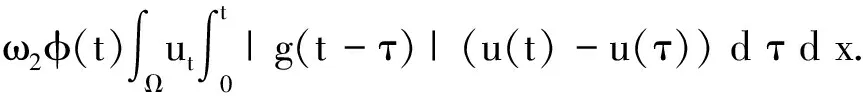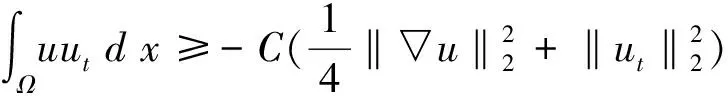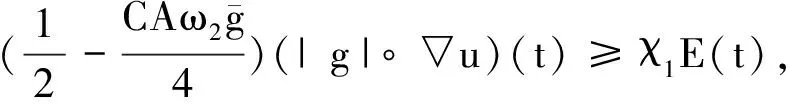一類帶有記憶核的黏彈性方程解的能量衰減估計
岳香英, 蒲志林
(四川師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院, 四川 成都 610066)
1 引言及預(yù)備知識
本文考慮以下帶有記憶項的黏彈性方程的柯西問題
utt(x,t)-Δu(x,t)+
u(x,0)=u0(x),
ut(x,0)=u1(x),x∈Ω,
(1)
其中,Ω是Rn(n∈N)中的有界區(qū)域,u0、u1為初值,g是定義在Ω上的函數(shù),是方程的記憶項,稱為記憶核,也叫松弛函數(shù).
已有大量的學(xué)者對黏彈性方程的動力學(xué)行為進行了研究,例如文獻[1-5].從已知的研究結(jié)果中知道,當g≡0時,系統(tǒng)的能量值為常數(shù),當g≠0時,以下是一些關(guān)于黏彈性系統(tǒng)解的漸近行為的結(jié)果:文獻[6-7]確定了黏彈性方程的解的存在性,并表明隨著時間趨于無窮,黏彈性系統(tǒng)的解趨于零,但是并沒有計算出明確的衰減率.當記憶核g呈g=e-αt即指數(shù)衰減的形式時,文獻[8-9]得出了非線性黏彈性方程解的指數(shù)衰減率.文獻[10-14]的研究結(jié)果表明在有界區(qū)域上,黏彈性方程解的衰減率依賴于記憶核g的衰減率,即當記憶核g呈指數(shù)衰減時,方程的解也是呈指數(shù)衰減,而當記憶核g呈多項式衰減時,方程的解也以相同的衰減率呈多項式衰減.Rivera等[15]研究了方程
(2)
其中A是某個Hilbert空間上的正自伴算子.證明了當0≤α<1時,方程記憶項g的衰減不足以使方程的解產(chǎn)生指數(shù)衰減的穩(wěn)定形式,但在一定的條件下,可以使方程的解呈多項式衰減.
在之前的研究中,記憶函數(shù)g都有衰減的特性.關(guān)于記憶函數(shù)g都有如下的假設(shè)
g(0)>0,g′(t)≤-αg(t), ?t≥0,
(3)
其中,α>0.上述假設(shè)條件太過嚴苛,已有許多文獻在討論放寬這一假設(shè)[16-21].特別地,文獻[18]在Rn中對記憶函數(shù)g做了如下假設(shè)
g(0)>0,g′(t)+αg(t)≥0, ?t≥0. (4)
在這個假設(shè)中,g′(t)可以取正值,即說明記憶函數(shù)g可以適當遞增,而不是一直衰減的,并且在該假設(shè)條件下,得到了方程的解是呈多項式衰減的.文獻[19]關(guān)于記憶函數(shù)g做了如下假設(shè):
g∈W2,1(R+)∩C2(R+),g(0)>0,
(5)
其中α和Cg是正常數(shù).在該假設(shè)下,g、g′和g″可以變號,所得結(jié)果是當記憶核g呈指數(shù)衰減時,方程的解也是呈指數(shù)衰減,而當記憶核g呈多項式衰減時,方程的解也以相同的衰減率呈多項式衰減.
本文受文獻[18-19]啟發(fā),不再局限于g>0以及g具有一致衰減特性,建立了新的假設(shè),并構(gòu)造了方程(1)的能量泛函.對能量泛函進行估計,得到方程(1)的解的漸近性,以及在|g|呈指數(shù)衰減時,方程的解依據(jù) φ(t)的不同呈相應(yīng)的衰減方式.
本文對記憶核 g作如下假設(shè):
( C1)g:R+→R是一個可微函數(shù),滿足
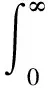
(C2) 存在可微函數(shù)φ>0以及常數(shù)r>0和h>0滿足
|g(t)|′≤-φ(t)|g(t)|,t≥0,
φ′(t)≤0, ?t≥0.
該假設(shè)拓寬了假設(shè)(4)的應(yīng)用范圍,即g的符號不要求一定為正,也可以為負,同時弱化了假設(shè)(5)中g(shù)二階可導(dǎo)的要求.相較于假設(shè)(4)和(5),本文的假設(shè)條件應(yīng)用更為廣泛和一般.
記
引理 1.1[16]若假設(shè)(C1)和(C2)成立,且
u0∈H1(Ω),u1∈L2(Ω),
則問題(1)存在唯一的解滿足:
u∈C([0,∞),H1(Ω)),
ut∈C([0,∞),L2(Ω)).
引理 1.2[18]當1≤p 存在一個常數(shù)C=C(n,p),使得 ‖u‖p*≤C‖▽u‖p, ?u∈W1,p(Ω). (6) 定義能量泛函 其中 引理 1.3若u是方程(1)的解,則能量泛函滿足 (7) 其中N和H是正常數(shù). 證明對能量泛函兩邊求導(dǎo),可得 E′(t)=(▽u(t),▽ut)+ (8) 其中 (9) 對(9)式的第二項進行估計,則存在常數(shù)N>0和H>0, dxdτ≤ (10) 由于|g|是非增函數(shù),所以 |g(t)|≤|g(0)|=g(0)=K. 對(8)式第二項進行估計 由(8)~(11)式可得到(7)式. 引理 2.1若u是系統(tǒng)(1)的解,定義輔助泛函 在假設(shè)(C1)和(C2)條件下,則存在某個常數(shù)ξ1>0使得 (12) 證明對Ψ1(t)求導(dǎo),可得 (13) 由(1)式可得 (14) 所以 (15) 由(5)式可得 C‖▽u‖2‖ut‖2≤ (16) 對(14)式的第二項進行估計,可得 |▽u(t)|)dτ)2dx. (17) 由Young不等式可得 |▽u(t)|)dτ)2dx≤ (18) 由(15)~(18)式可得 引理 2.2若u是系統(tǒng)(1)的解,定義輔助泛函 (u(t)-u(τ))dτdx, 則存在某個常數(shù)ξ2,在t≥0時滿足 (20) 證明直接對Ψ2(t)求導(dǎo),可得 (u(t)-u(τ))dτdx- (21) 其中 (22) 對于(21)式中的第二項,由(1)式可得 對于(21)式中的第一項,可得 (24) 對于(23)式中的第一項,可得 (25) 對于(23)式中的第二項,可得 |▽u(t)|)dτ)2dx+ 由Young不等式及假設(shè)(C2)可得 (27) 將(22)~(27)式代入(21)式,則(20)式成立. 引理 2.3假設(shè)(C1)和(C2)成立,構(gòu)造輔助泛函 F(t)=E(t)+ω1Ψ1(t)+ω2Ψ2(t). (28) 取適當?shù)?個正常數(shù)χ1、χ2,使其滿足 χ1E(t)≤F(t)≤χ2E(t),t≥t0, (29) 其中t0是足夠大的值,使得ω1、ω2充分小. 證明把E(t)、Ψ1(t)、Ψ2(t)、Ψ3(t)代入(24)式,可得 (30) 由Cauchy-Schwarz不等式、Young不等式和(6)式可得 (31) 和 (32) 由假設(shè)(C2)知φ(t)為單調(diào)減函數(shù),則有 φ(t)≤φ(0)=A. (33) 將(31)~(33)式代入(30)式可得 同理可得 (35) 和 (36) 下面將(33)~(35)式代入(28)式,可得 其中ω1和ω2充分小,可得 F(t)≥χ1E(t),t≥t0,χ1>0. (38) 聯(lián)立(34)和(37)式,可得到結(jié)論. 定理 2.1假設(shè)(C1)和(C2)成立,且u0∈H1(Ω),u1∈L2(Ω),以及引理1.3的條件成立,則存在正常數(shù)P和p,使得 證明對(28)式求導(dǎo),并由(7)、(12)、(20)式及假設(shè)(C2)可得 -[ω2(1-m-ξ2(r+1))- hN]φ(t)(|g|°▽u)(t). (39) 由假設(shè)(C2)知 φ(t)(|g|°▽u)(t)≤ |▽u(τ)-▽u(t)|2dτdx+ φ(t)(|g|°▽u)(t)≤ hN]φ(t)(|g|°▽u)(t), (40) 所以 F′(t)≤-[ω2(1-m-ξ2(r+1))- hN]φ(t)(|g|°▽u)(t). (41) 選擇合適的ξ1和ξ2使得 若選定ξ1和ξ2,選擇合適的ω1和ω2滿足條件 (42) 使得 ω2(1-m-ξ2(r+1))- 因為g是連續(xù)且g(0)>0,所以對任意的t≥t0>0有 (43) 取 P0=min{k1,k2,k3}, 則可得 F′(t)≤-P0φ(t)E(t). 又由(29)式可得 (44) 對(44)式在(t0,t)上積分可得 (45) 又由(29)和(45)式可得 (46) 故定理2.1得證.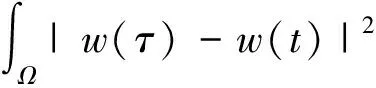
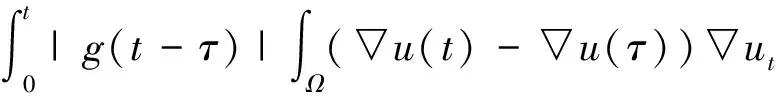
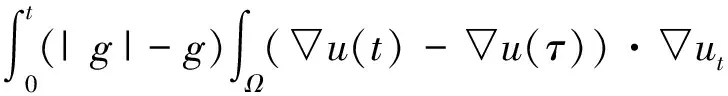
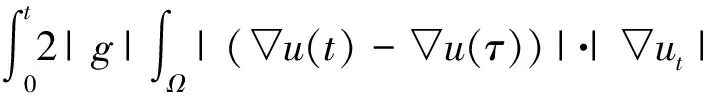
2 能量衰減估計