一類混合變分不等式的可變度量慣性近似點算法

余 靜, 夏福全

(四川師范大學 數學科學學院, 四川 成都 610066 )

本文總假設Rn為歐式空間,〈·,·〉和‖·‖ 分別表示Rn的標準內積和l2范數.

設W?Rn是非空閉凸子集,θ:Rn→R是下半連續凸函數,F:Rn→Rn是單值映射.本文所研究的混合變分不等式問題(MVIP)為:求w*∈W,使得

θ(w)-θ(w*)+〈w-w*,F(w*)〉≥0,

?w∈W.

(1)

顯然問題(1)等價于:求w*∈W,使得

0∈(F+?(θ+IW))(w*)，

(2)

其中IW表示集合W的指示函數,其定義為

?f表示函數f:Rn→R的次微分,其定義為:對?x∈Rn,

?f(x)={ξ∈Rn|f(y)-f(x)≥

〈ξ,y-x〉,y∈Rn}.

顯然,問題(2)是極大單調包含問題的特例.極大單調包含問題即為:求w*∈Rn,使得

0∈T(w*),

(3)

其中T:Rn?Rn是極大單調集值映射.對于極大單調包含問題(3),已經有很多的算法,方法之一為經典的近似點算法(PPA).為了獲得下一步迭代點wk+1,經典近似點算法需要求解近似子問題

0∈λkT(w)+w-wk,

(4)

其中,wk是當前迭代點,λk是正的參數.對于問題(4),Parente等[1]提出了廣義近似子問題

0∈λkMkT(w)+w-wk,

(5)

其中Mk為n階對稱正定矩陣.顯然問題(5)等價于

(6)

0∈λkT(w)+Gk(w-wk).

(7)

另一方面,Alvarez等[2]研究了極大單調包含問題(3)的慣性近似點算法,迭代如下:任給wk-1,wk∈Rn,參數序列αk∈[0,1],λk>0,求wk+1∈Rn使得

(8)

如果(8)式中的αk≡0,k=0,1,2，…,則以上迭代就退化為經典近似點迭代.如果αk和λk滿足一定的條件,并且T-1(0)≠?,Alvarez等[2]證明了由(8)式產生的迭代序列{wk}收斂于T-1(0)中的點.隨后,Alvarez[3]證明了慣性的實施加快了(8)式中迭代序列的收斂速度.

最近,Chen等[4]應用Alvarez等[2]的思想,提出了求解問題(1)的一般慣性近似點算法.算法如下:

設G是n階半正定對稱矩陣,給定參數列

{αk≥0:k=0,1,2,…}, {λk>0:k=0,1,2,…}.

對任給w0=w-1∈Rn,求wk+1∈W,k=0,1,2,…,使得

θ(w)-θ(wk+1)+〈w-wk+1,F(wk+1)+

(9)

(i) 問題(1)的解集W*≠?;

(ii) 映射F是H-單調,即對?u,v∈Rn有

其中H是n階半正定對稱矩陣;

(iii)G+H是正定矩陣.

對于假設條件(ii)和(iii),當映射F是單調映射時,即矩陣H≡0時，G為對稱正定矩陣.

顯然(9)式等價于

(10)

其中T=F+?(θ+IW).

受到(7)和(10)式的啟發,本文將研究一般混合變分不等式問題(1)的變度量慣性算法.具體方法是:在算法中,將近似子問題(10)中的不變矩陣G變為可變對稱正定矩陣Gk,獲得算法的可變度量慣性近似子問題

(11)

本文在Chen等[4]相似的假設條件下,獲得了算法的全局收斂性和收斂率方面的結果.

1 預備知識

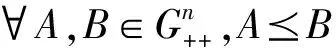
設λmin(G)、λmax(G)分別為矩陣G的最小特征值與最大特征值.易知,如果存在λl,λu>0,使得λl≤λmin(G)≤λmax(G)≤λu,則有

(12)

下面給出單調映射的定義以及下半連續函數的定義,定義1.1參見文獻[5],定義1.2參見文獻[6].

定義 1.1[5]設F:Rn→Rn,如果對任意x,y∈Rn,均有

〈x-y,F(x)-F(y)〉≥0,

則稱映射F在Rn上單調.

定義 1.2[6]設f:Rn→R,若對任意收斂于x的點列{xk}?Rn均有

則稱函數f:Rn→R在x處下半連續.如果函數f在Rn上每一點均下半連續,則稱f在Rn上下半連續.

首先證明一些有用的性質.

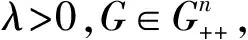
P(·)=(I+λG-1T)-1(·),

則P:Rn→Rn是單值映射且是G范數下的非擴張映射.

證明對?x∈Rn,若存在z1,z2∈Rn,且z1≠z2,使得

z1=P(x)=(I+λG-1T)-1(x),

z2=P(x)=(I+λG-1T)-1(x).

易知

x∈(I+λG-1T)(z1)=z1+λG-1T(z1),

x∈(I+λG-1T)(z2)=z2+λG-1T(z2).

進而有

λ-1G(x-z1)∈T(z1),

λ-1G(x-z2)∈T(z2).

由T的單調性有

〈λ-1G(x-z1)-

λ-1G(x-z2),z1-z2〉≥0.

(13)

由(13)式可得

〈λ-1G(z2-z1),z1-z2〉≥0.

(14)

由(14)式及λ>0可得

〈G(z1-z2),z1-z2〉≤0.

(15)

下面證明P為G范數下的非擴張映射.對?x,y∈Rn且u=P(x),v=P(y).下證

‖u-v‖G≤‖x-y‖G.

事實上,由u=P(x),v=P(y)有

x∈(I+λG-1T)(u)=u+λG-1T(u),

y∈(I+λG-1T)(v)=v+λG-1T(v).

從而存在z1∈T(u),z2∈T(v)使得x=u+λG-1z1,y=v+λG-1z2.因此

2λ〈u-v,G-1(z1-z2)〉G=

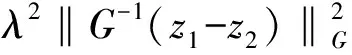
性質 1.4設W?Rn是非空閉凸子集,θ:Rn→R是下半連續凸函數,F:Rn→Rn是單調單值映射,令T(·)=[F+?(θ+IW)](·),則T-1(0)∩W=W*,其中W*表示問題(1)的解集.

證明顯然T:Rn?Rn為單調集值映射.對?w*∈T-1(0)∩W,有0∈T(w*).由T的定義知

0∈F(w*)+?(φ+IW)(w*).

從而,存在ξ∈?(φ+IW)(w*),使得0=F(w*)+ξ.根據次微分的定義知ξ滿足

(φ+IW)(w)-(φ+IW)(w*)≥〈ξ,w-w*〉,

?w∈Rn.

(16)

將ξ=-F(w*)代入(16)式可得

(φ+IW)(w)-(φ+IW)(w*)≥

〈-F(w*),w-w*〉, ?w∈Rn.

(17)

由(17)式及w*∈W可得

φ(w)+IW(w)-φ(w*)≥

〈-F(w*),w-w*〉, ?w∈Rn.

(18)

由(18)式及對?w∈W有

φ(w)-φ(w*)≥〈-F(w*),w-w*〉.

(19)

由(19)式可得

φ(w)-φ(w*)+〈w-w*,F(w*)〉≥0.

因此,w*∈W*,故T-1(0)∩W?W*.

另一方面,對?w*∈W*有

φ(w)-φ(w*)+〈w-w*,F(w*)〉≥0,

?w∈W.

(20)

由(20)式及次微分的定義可得

-F(w*)∈?(φ+IW)(w*).

(21)

由(21)式可得

0∈F(w*)+?(φ+IW)(w*)，

也即0∈T(w*),因此w*∈T-1(0)∩W,故W*?T-1(0)∩W.

2 算法及收斂性

下面給出可變度量慣性近似點算法,并在合適的假設條件下證明算法的序列全局收斂,建立算法的非線性O(1/k)收斂率.

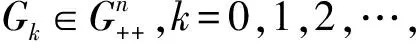
θ(w)-θ(wk+1)+〈w-wk+1,F(wk+1)+

(22)

本文總假設下面的條件成立：

(i)W*≠?;

(ii)F:Rn→Rn為單調映射;

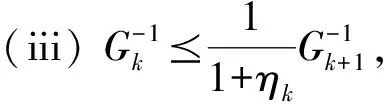
λl≤λmin(Gk)≤λmax(Gk)≤λu.

假設(ii)保證了(22)式中的wk+1是唯一存在的,因此,算法2.1是良定的.下面證明由算法2.1得到的序列全局收斂性.

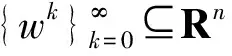
(23)

證明任取w*∈W*.令

其中T(·)=[F+?(θ+IW)](·).由性質1.4有w*∈T-1(0),從而

由(22)式及次微分的定義可知

根據上述兩式以及Pk的非擴張性可得

2αk〈wk-w*,wk-wk-1〉Gk=

(24)

由假設(iii)可得(1+ηk)Gk+1?Gk.因此

(25)

聯合不等式(24)和(25)可得

(26)

上式中的第二個不等式是由αk≤ηk獲得.由不等式(26)可得

(27)

上式中的等式是由w0=w-1獲得,第三個不等式是由(23)式獲得.由(12)式及假設條件(iii)可得

聯合不等式(27)和(28)可得

(29)

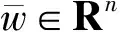
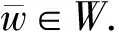
θ(w)-θ(wkj)+〈w-wkj,F(wkj)〉≥

αkj-1(wkj-1-wkj-2)‖Gkj-1≥

-λ-1‖w-wkj‖Gkj-1‖wkj-wkj-1‖Gkj-1-

-λ-1λu‖w-wkj‖‖wkj-wkj-1‖-

(30)

上式中的第三個不等式是由Cauchy-Schwarz不等式獲得,第四個不等式是由λk≥λ,αk≤αu獲得,最后一個不等式是由(12)式及假設條(iii)獲得.由0<αl≤αk可得

再由(23)式可得

因此,根據0<αl≤αk可得

進一步根據(12)式及假設條件(iii)有

因此,(30)式兩邊同時讓j→∞,可得

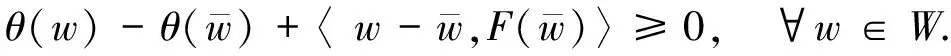
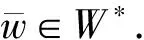
(31)

即

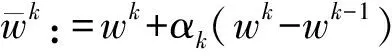
(32)

顯然

(33)

(34)

將(33)和(34)式代入(32)式整理可得

(35)

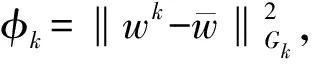
代入(35)式可得

(1+ηk)φk+1-(1+αk)φk≤

(36)

由1+αk≤1+ηk,αk>0及(36)式可得

(1+αk)(φk+1-φk)≤

(37)

由(37)式可得

φk+1-φk≤

(38)

由0<αl≤αk及(38)式可得

(39)

由(39)式可得

(40)

上式中的第二個不等式是由(23)式獲得.由(40)式可得

由(12)式及假設(iii)可得

因此

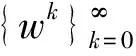
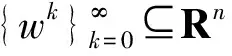
(b) 對?w*∈W*,?k∈N+,有

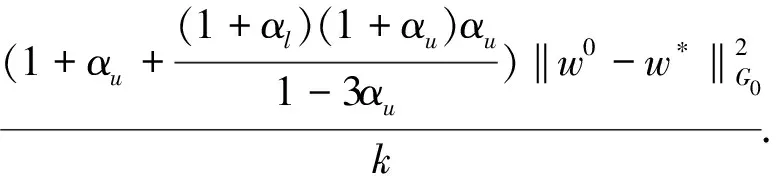
(41)

證明設w*∈W*,將w=w*代入(22)式,并由F的單調性可得

θ(w*)-θ(wk+1)-〈wk+1-w*,F(wk+1)〉≤

θ(w*)-θ(wk+1)-〈wk+1-w*,F(w*)〉-

〈wk+1-w*,F(wk+1)-F(w*)〉≤0，

即

(42)

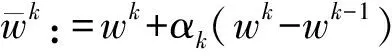
〈wk+1-w*,wk+1-wk〉Gk-

αk〈wk+1-w*,wk-wk-1〉Gk≤0.

(43)

顯然

(44)

2〈wk+1-w*,wk-wk-1〉Gk=

(45)

將(44)和(45)式代入(43)式整理可得

(46)

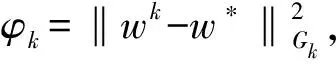
代入(46)式可得

(1+ηk)φk+1-(1+αk)φk≤

(47)

由1+αk≤1+ηk,αk>0及(47)式可得

(1+αk)(φk+1-φk)≤

(48)

由(48)式可得

(49)

上式中的第二個不等式是由Cauchy-Schwarz不等式獲得,第三個不等式是由假設(iii)獲得,最后一個不等式是由ηk>0獲得.

令

由(49)式可得

uk+1-uk=φk+1+

(50)

上式中的第二個不等式是由αk≤αk+1獲得,最后一個不等式是由αl≤αk≤αu獲得.由(50)式及αu<1/3可知{uk}是非增序列,且uk≥0,k=0,1,2,…,則

(51)

由(51)式可得

u0-uk+1≤φ0,

(52)

上式中的第二個不等式是由w0=w-1獲得.由(52)式可得

(53)

由αk≤αu及(53)式可得

故由定理2.2可知結論(a)成立.由(49)式的第一個不等式可得,對?i≥0有

(54)

由αi≤αu及(54)式可得

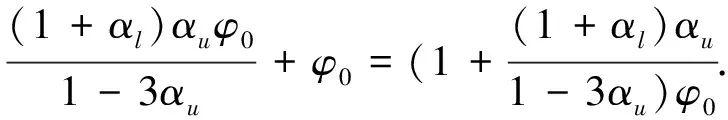
由(55)式可得

(56)

由(56)式及

可推得(41)式成立.

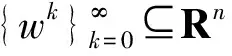
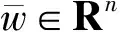
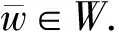
θ(w)-θ(wkj)+〈w-wkj,F(wkj)〉≥

αkj-1(wkj-1-wkj-2)‖Gkj-1≥

-λ-1‖w-wkj‖Gkj-1‖wkj-wkj-1‖Gkj-1-

-λ-1λu‖w-wkj‖‖wkj-wkj-1‖-

(57)

上式中的第三個不等式是由Cauchy-Schwarz不等式獲得,第四個不等式是由λk≥λ,αk≤αu獲得,最后一個不等式是由(12)式及假設條件(iii)獲得.由0<αl≤αk可得

再由(23)式可得

因此,根據0<αl≤αk可得

進一步根據(12)式及假設條件(iii)有

因此,(57)式兩邊同時讓j→∞,可得

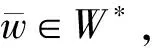
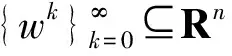
證明由定理2.2及定理2.4結論顯然成立.