一類具有常數輸入和馬氏轉換的SIQRS模型

趙曉靜, 張 龍, 張德婷

(新疆大學 數學與系統科學學院, 新疆 烏魯木齊 830046)

0 引言及模型建立

近年來,傳染病動力學發展迅速,人們建立了大量的流行病模型,如SIS、SIRS、 SIER和SIQR等,并取得了很多重要結果[1].在傳染病模型中,發病率函數對于環境波動的影響最為敏感,因此它扮演著1個關鍵性的角色,確保模型能合理地描述疾病流行的動態[2].一般地,都假設疾病傳播的發生率為雙線型,即βSI，如文獻[3]建立了具有隔離項和雙線性疾病發生率的SIQR模型

(1)

但事實上,1個人的傳染力是有限的,所以考慮飽和發生率更符合實際,也更有意義.此外,上述模型并沒有考慮外界環境的隨機影響.在實際生活中,疾病所處的環境因素并不是一成不變的,不同環境中疾病的表現也不同.比如說,在比較潮濕的紫外線較低的環境中,疾病的存活性和傳染性更強,而在紫外線較高的干燥環境中,存活性和傳染性較差[4-6].種群的增長率和環境的容納量會隨食物資源的豐度變化而有所不同,因為食物資源的豐度在很大程度上依賴于不可預知的降水等問題[7],因此,很多研究學家開始關注這一現象.Gray等[8]首先提出用帶有馬氏轉換的傳染病模型來進行刻畫,并得到了一些很好的結論.關于馬爾克夫轉換的傳染病模型,Li等[9]已經做出了很好的總結.國內外學者雖然對隨機傳染病模型的研究有了一定的成就,但對于帶有馬氏轉換的SIQRS模型研究卻較少.因此研究帶有馬氏轉換且疾病發生率為飽和的SIQRS傳染病模型是很有實際意義的.

由此,建立了SIQRS傳染病模型

(2)

其中,S(t)代表易感者類,I(t)代表普通染病者類,Q(t)代表染病隔離者類,R(t)代表移除者類,總人口數為N(t)=S(t)+I(t)+Q(t)+R(t).Λ代表新增易感者人數,μ代表人均自然死亡率系數,α代表因病死亡率系數,δ代表隔離率系數,γ和ε代表普通染病者和染病隔離者的恢復率系數,λ表示免疫消失率系數.疾病傳播率系數β由時齊馬氏鏈{r(t),t≥0}表示,r(t)在有限的狀態空間Μ={1,2,…,E}中取值,表示不同的環境.

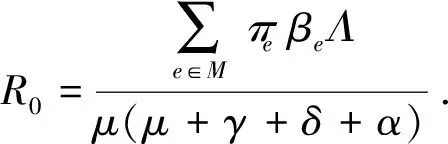
1 預備知識

在本文中,做如下假設:

(H)g(x)在[0,Λ/μ]滿足Lipschitz性質,即存在常數θ>0,使得對任意x1,x2∈[0,Λ/μ],滿足

|g(x1)-g(x2)|≤θ|x1-x2|,

為研究系統的動力學,需要引入下面的引理.

引理 1若x*∈R4是系統

的1個全局漸進穩定的平衡點,則對x*的任意鄰域U和任意緊集C?R4,存在T>0,使得對所有t≥T和x0∈C有x(t,x0)∈U成立.

2 主要結果

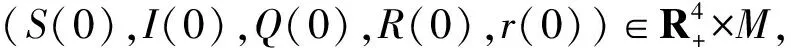
下證此解具有全局性,則只需證明τe=∞a.s.,令k0≥1充分大使得S(0),I(0),Q(0),R(0)∈[1/k0,k0].記inf ?=∞(?代表空集).對任意k≥k0,定義停時

τk={t∈[0,τe) :min{S(t),I(t),Q(t),R(t)}≤

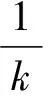
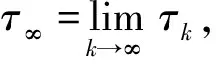
Ρ{τ∞≤T}>ε.

故存在整數k1≥k0,使得

Ρ{τk≤T}≥ε,k≥k1.

(3)

(I-1-lnI)+(Q-1-lnQ)+(R-1-lnR).

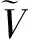
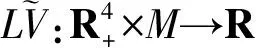
Λ-μ(S+I+Q+R)+4μ+

其中K為正常數,且與S、I、Q、R、e無關,因此有

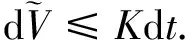
(4)

對(4)式從0到τk∧T積分并取期望得

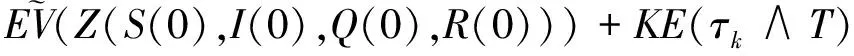
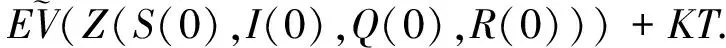
(5)

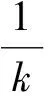
則有

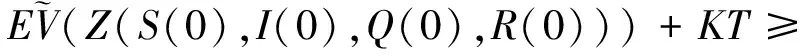
其中,IΩk表示Ωk的示性函數.令k→∞,則有

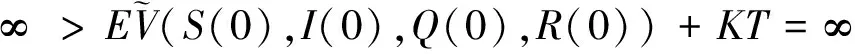
矛盾,所以τ∞=∞ a.s..故τe=∞ a.s..

令N=S+I+Q+R,則

(μ+γ+δ+α)I+δI-(μ+η+α)Q+γI+ηQ-

(μ+λ)R=Λ-μ(S+I+Q+R)-α(I+Q),

所以

由常數變易公式計算得

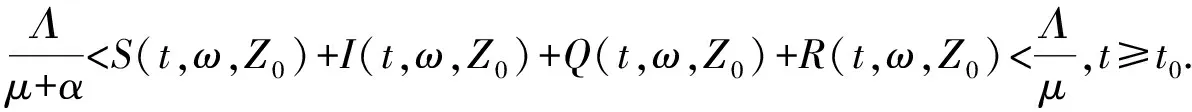
命題 3對R0值的以下替代條件成立:

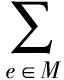
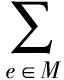
由于這個定理的證明可以直接得出,故這里省略.

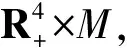
(6)

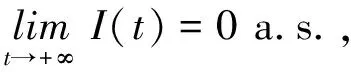
(7)

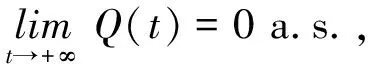
(8)

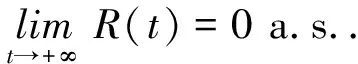
(9)

證明第一步,證明(7)式成立.由系統(2)的第二個方程知

則

由命題3的(i)知

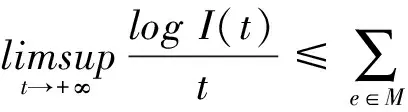
故

即(7)式成立.

第二步,證明(8)式成立.

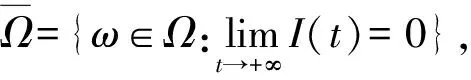
由比較原理知

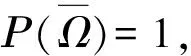
第三步,證明(9)式成立.

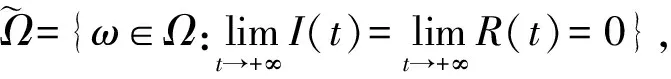
由比較原理知

同理第二步可得

即(9)式成立.

第四步,證明(6)式成立.

令N(t)=S(t)+I(t)+Q(t)+R(t),由系統(2)可知

解得

所以

由ε3的任意性知

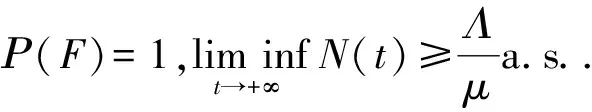
另一方面,由引理2知

所以

故得

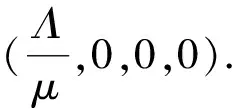
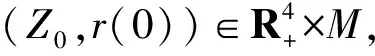
證明由系統(2)的第二個方程知

則

對上式兩邊積分得

(10)

又因為

所以

將上式代入到(10)式得

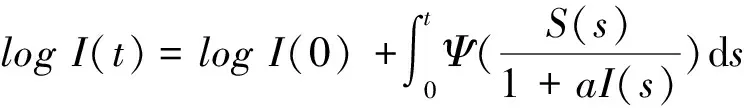
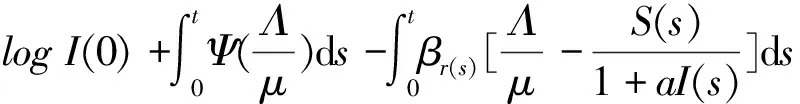
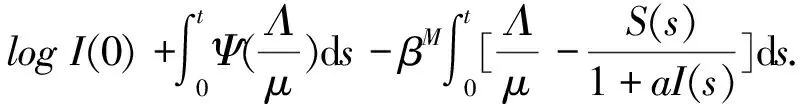
由系統的第一個方程知

對上述不等式兩邊積分得

故

(12)

將(12)式代入到(11)式得

所以

證畢.

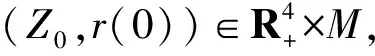
推論 6對任意初值(Z0,r(0))∈X,系統的解(S(t),I(t),Q(t),R(t)),滿足:

(i) 若R0<1,則系統(2)的染病者的數目將幾乎確定指數收斂于0的概率為1;

(ii) 若R0>1,則疾病幾乎確定持久.

3 數值模擬

在本節中，對系統(2)進行數值模擬，令M={1,2},Λ=1.3,μ=0.046,λ=0.027,a=0.001 3,γ=0.004 6,δ=0.452 0,α=0.003 5,η=0.008,且這些參數保持不變.為方便對比,設S(0)、I(0)、Q(0)和R(0)在狀態1和狀態2的初始值相同,即S(0)=40,I(0)=10,Q(0)=5,R(0)=5.在狀態1,β1=0.038,相對應的基本再生數R1=2.122 0>1,此時,S(t)、I(t)、Q(t)和R(t)隨時間t的變化如圖1所示,疾病持久.在狀態2,β2=0.012,相對應的基本再生數R2=0.670 1<1,此時,S(t)、I(t)、Q(t)和R(t)隨時間t的變化如圖2所示,疾病消失.

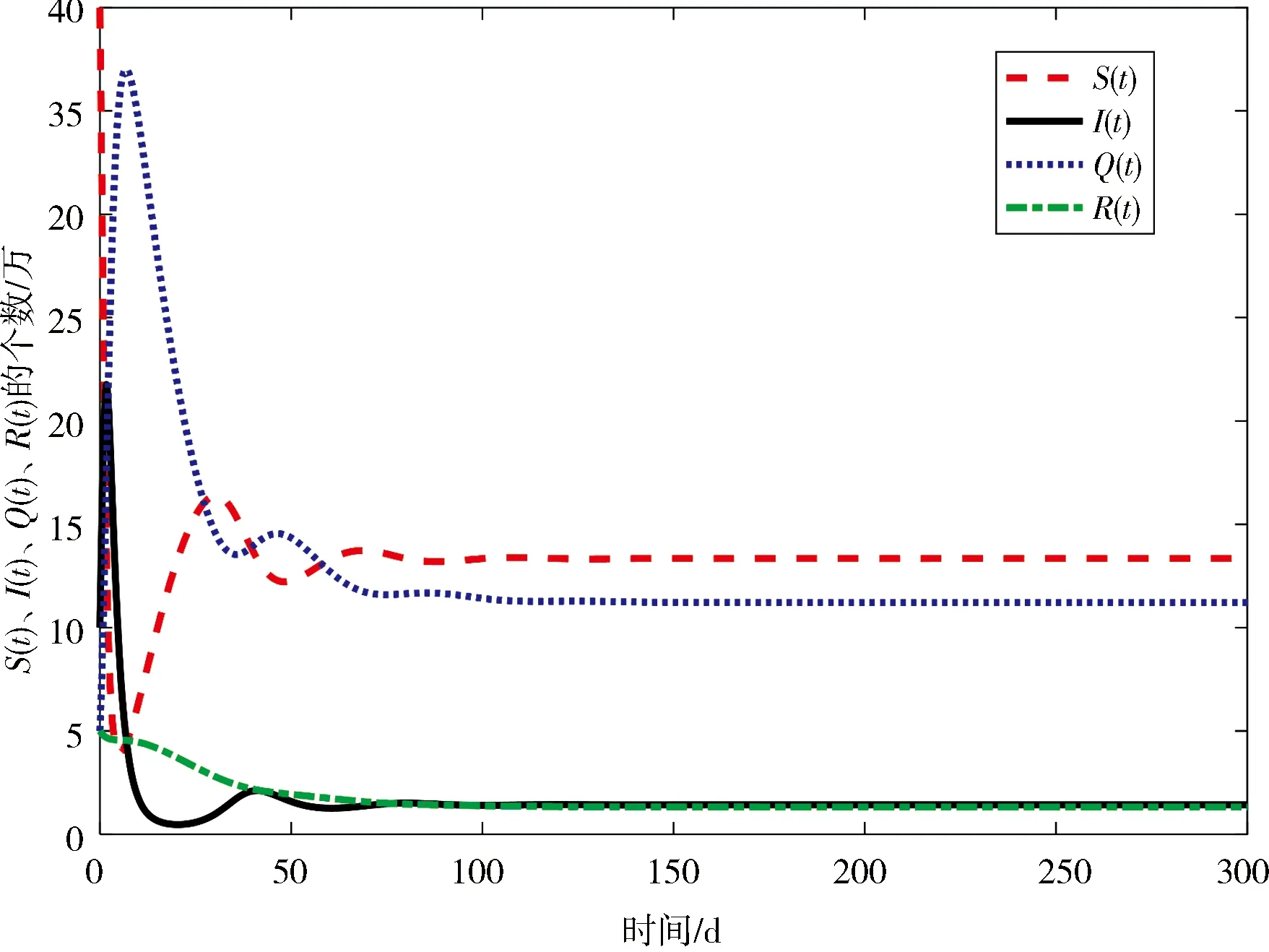
圖 1 S(t)、I(t)、Q(t)和R(t)在β1=0.038時的時間序列圖

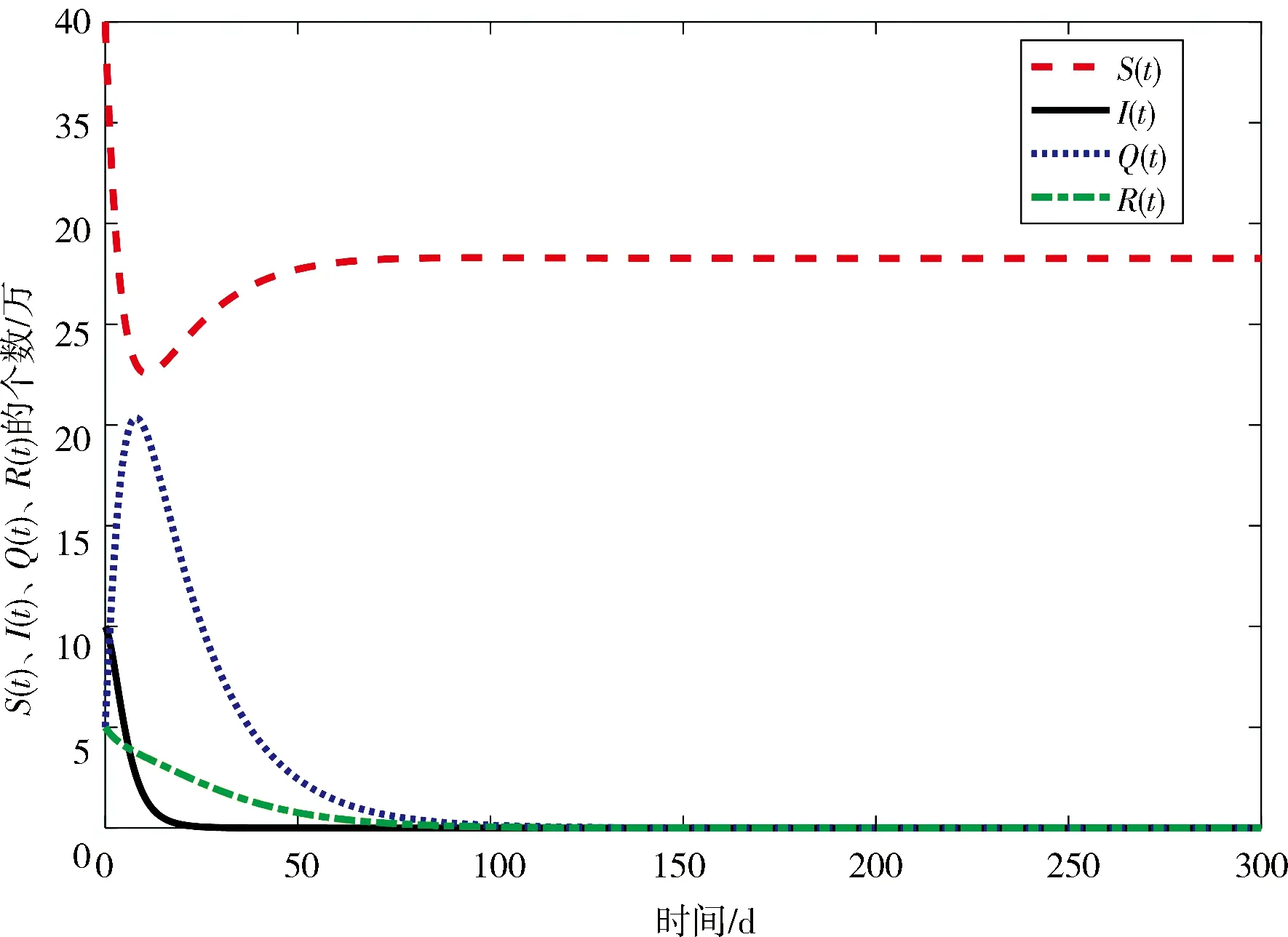
圖 2S(t)、I(t)、Q(t)和R(t)在β2=0.012時的時間序列圖

Fig.2ThetimeseriesdiagramofS(t),I(t),Q(t),R(t)atβ2=0.012

若取Π=(π1,π2)=(0.5,0.5),對應的R0=1.396 1>1,S(t),I(t),Q(t),R(t)在狀態1和狀態2之間隨時間t的變化如圖3所示,疾病隨機持久.若取Π=(π1,π2)=(0.2,0.8),則對應的R0=0.960 5<1,S(t),I(t),Q(t),R(t)在狀態1和狀態2之間隨時間t的變化如圖4所示,疾病隨機消除.

圖 3 S(t)、I(t)、Q(t)和R(t)在β1=0.038和β2=0.012之間隨機切換下的時間序列圖

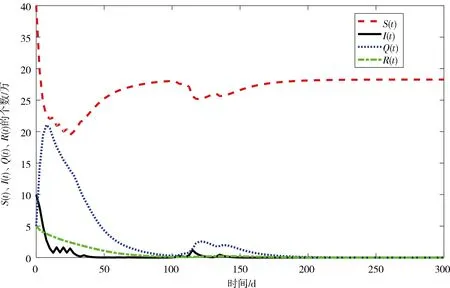
圖 4 S(t)、I(t)、Q(t)和R(t)在β1=0.038和β2=0.012之間隨機切換下的時間序列圖

致謝新疆大學博士科研啟動基金(BS160204)、新疆大學博士創新項目(XJUBSCX-2017005) 和自治區普通高等學校科研計劃項目(XJEDU2017T001)對本文給予了資助，謹致謝意.