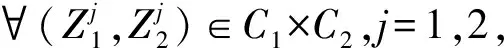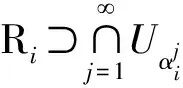n方體連續自映射混沌集合的Hausdorff維數
吳華明
(嶺南師范學院 數學與統計學院, 廣東 湛江 524048)
Ivan[1]在1988年用Lebesgue測度作為標準來研究線段自映射混沌集合的大小,得到了C0(I)中存在一個剩余集R,使得對于每一個映射f∈R,對于f而言的每一個Li-Yorke混沌集合[2]的Lebesgue測度為0.顧榮寶[3]用Hausdorff維數作為度量的標準來研究線段自映射混沌集合的大小,得到了C0(I)中也存在一個剩余集R,使得對于每一個映射f∈R,若C?I對于每一個f而言是Li-Yorke混沌的,則C的Hausdorff維數dimH(C)=0.文獻[4]將結果推廣到I2上有類似的結論.本文將文獻[4]的結果推廣到高維的情形.
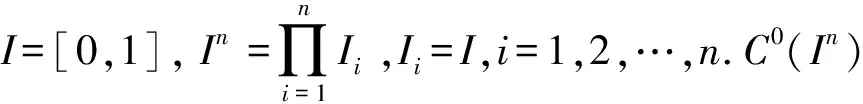
本文主要結果是:存在剩余集R ?C0(In),使得對每個f∈R,若C?In對f而言是Li-Yorke混沌的,則C的Hausdorff維數dimH(C)≤n-1,并且C是第一范疇集.
該結果對高維笛卡爾積的情形也成立,即在C0(Ini,Ini)中存在一個剩余集Ri,使得對于每個fi∈Ri,i=1,2,若集合Ci?Ini對于fi而言是Li-Yorke混沌的,則dimH(C1×C2)≤n-1,且C1×C2是第一范疇集.
1 預備知識
1.1 方體
定義 1設m是任一正整數,
A={(t1,…,tm)|ri≤ti≤si, i=1,2,…,m}?Rm
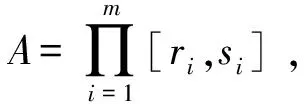
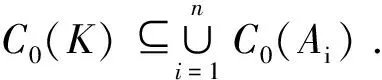
顯然Ai均是K的閉子集,根據黏合引理,若有連續映射族fi:Ai→Rl,使任意2個在公共面上的取值相同,則有連續映射:f:K→Rl,使f|Ai=fi.
1.2 方體的面
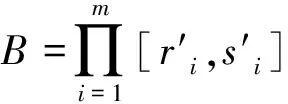
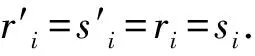
2) 當ri 易見,若BA,則: 1)B?A, 2) 0≤ dim B≤dimA, 在方體A的面中,有2個特殊的面A0和A1,分別稱為方體A的前面和后面,其中 當rm=sm時,A0=A1=A;當rm dimA0=dimA1=dimA-1. 顯然C0(A)=C0(A0)∪C0(A1). 對?x=(t1,…,tm)∈A,稱點 x0=(t1,…,tm-1,rm)∈A0, x1=(t1,…,tm-1,sm)∈A1 分別為x的前影和后影,則x=(1-t)x0+tx1,其中t=(tm-rm)/(sm-rm),若rm 1.3 典型同構設k 設A為Rm中的方體,顯然P(A0)=p(A1)=p(A)是Rm中的方體,且p|A0和p|A1都是線性保內積的同胚.而且p|C0(A0):C0(A0)→C0(p(A))和p|C0(A1):C0(A1)→C0(p(A))是一一對應的,稱p|A0和p|A1為典型同構.若BA,則p(B)p(A). 1.4 方體上的多重線性擴充任給g0:C0(A)→Rl,對m歸納地定義g:A→Rl如下:當m=1時,A=[r1,s1],若r1=s1,則A為單點,令g=g0即可;若r1 g(t1)=(1-t)g0(r1)+tg(s1),t1∈A, 其中t=(t1-r1)/(s1-r1),此時,稱g為g0的多重線性擴充. 上述的g有性質: (Ⅰ)g|C0(A)=g0; (Ⅱ)g連續; (Ⅲ)g(A)?[g0(C0(A))],其中[g0(C0(A))]為g0(C0(A))的凸包; (Ⅳ) 設BA,則g|B是g0|C0(B)的多重線性擴充. 設當m=k-1時,滿足上列性質(Ⅰ)~(Ⅳ)的多重線性擴充g已定義,對m=k時定義映射g,且稱滿足性質(Ⅰ)~(Ⅳ)的g為g0的多重線性擴充. 給定方體A?Rl,g0:C0(A)→Rl,則在Rk-1中的方體p(A)上,有2個函數: g(x)=(1-t)g′(p(x))+tg″(p(x)), 其中x=(t1,…,tk),t=(tk-rk)/(sk-rk),若rk 設K為Rm中的復合方體,g0:C0(K)→Rl,則g0限制在每個方體上都有一個多重線性擴充,由性質(Ⅳ),這些擴充在公共面上取值一致,故有連續映射g:K→Rl,使得它在頂點上與g0一致,在每個方體上的限制均為多重線性擴充,且g對于每個方體均滿足性質(Ⅲ).易見g也滿足性質(Ⅰ)和(Ⅱ). 定義 3設K為Rm中的復合方體,g0:C0(K)→Rl,則稱上述g為g0在K上的多重線性擴充. 為方便起見,先引入一些記號.Z+表示正整數集,m∈Z+,M=2m,η=2-2m2,ai=i/M,i=0,1,…,M;ci=(ai-1+ai)/2,i=1,2,…,M. Eim=[ai-1+η,ai-η], Fim=[ci-η,ci+η],i=1,2,…,M; Him=[ai-η,ai+η],i=1,2,…,M-1; H0m=[0,η],HMm=[1-η,1]; Cm={(ci1,ci2,…,cin)|i1,i2,…,in∈{1,2,…,M}}; Dm={a0,a0+η,a1-η,a1+η,…,aM-η,aM}; Qm={(z1,z2,…,zn)|zi1,…,zik∈{0,1},zik+1,…,zin∈Dm-{0,1},i1,i2,…,in為1,2,…,n的一個排列,k=1,2,…,n}. 引理 1R是C0(In)的剩余集. 對每個m∈Z+,Am顯然是C0(In)中的開集,事實上Am是C0(In)的緊致開拓撲的基元素. (1) 為一復合方體. 下面定義g0:C0(k)→In如下: (b) 對z=(z1,z2,…,zn)∈Qm,g0(z)為Cm中距離f(z1,z2,…,zn)最近的點(若這樣的點不唯一,可任取定一個),則存在g0在復合方體K上的多重線性擴充g,從而g(Em)?(Fm)0,即g∈Am. 往證ρ(f,g)<ε.對?(ci1,ci2,…,cin)∈Cm, 事實上有 |f(ci1,ci2,…,cin)-g(ci1,ci2,…,cin)|≤ 對于 ?z∈[ai1-1,ai1]×[ai2-1,ai2]×…×[ain-1,ain], 由(1)式有 |f(z)-f(ci1,ci2,…,cin)|<ε/5. (3) 事實上,由于[aij-1,aij]的長度不超過2-m,故 由(1)式有|f(z)-f(ci1,ci2,…,cin)|<ε/5,對?z∈Em. 由(2)和(3)式有 |f(z)-g(z)|<2ε/5. (4) 事實上 |f(z)-g(z)|≤|f(z)-f(ci1,…,cin)|+ |f(ci1,…,cin)-g(ci1,…,cin)|+ |g(ci1,…,cin)-g(z)|<2ε/5. 若(ci1,…,cin)∈Cm∪Qm,則 |f(ci1,…,cin)-f(ch1,…,chn)|<ε/5, hk=ik或ik+1, k=1,2,…,n. (5) 事實上 |(ci1,…,cin)-(ch1,…,chn)|≤ 由(1)式有 |f(ci1,…,cin)-f(ch1,…,chn)|<ε/5. 由(2)式和(a)、(b)有 |g(ci1,…,cin)-g(ch1,…,chn)|<3ε/5. (6) 事實上 |g(ci1,…,cin)-g(ch1,…,chn)|= |g(ci1,…,cin)-f(ci1,…,cin)+ f(ci1,…,cin)-f(ch1,…,chn)+ f(ch1,…,chn)-g(ch1,…,chn)|≤ |g(ci1,…,cin)-f(ci1,…,cin)|+ |f(ci1,…,cin)-f(ch1,…,chn)|+ |f(ch1,…,chn)-g(ch1,…,chn)|<3ε/5. 且至少存在一個1≤t≤n,使 取(ci1,…,cin)為Cm∪Qm與z點距離最小的點(若這樣的點不唯一,可任取一個).若 |f(z)-g(z)|≤ |f(z)-f(ci1,…,cin)|+|f(ci1,…,cin)- g(ci1,…,cin)|+|g(ci1,…,cin)-g(z)|≤ ε/5+ε/5+|g(ci1,…,cin)-g(ci1,…,cin)|<ε. 因此,Bn是C0(In)的稠密開集,故R是C0(In)的剩余集. 引理 2對于任意f∈R,若集合C?In對于映射f而言是Li-Yorke混沌的,則存在嚴格遞增的正整數序列{nk},使得 (7) 證明設f∈R,則存在嚴格遞增的正整數序列{nj},使得對每個j∈N,f∈Anj,C對映射f而言是Li-Yorke混沌的.任給 (8) 只需證明z1與z2不能同時滿足Li-Yorke混沌定義的2個條件時(7)式成立,即證 (9) (10) 不能同時成立. Ηn-1+αδ(In(Enk)0)≤n(2m+1)(1/2η)n-1× |Gi1m×…×Gij-1m×Hijm×Gij+1m×…×Ginm|n-1+α≤ n1+(n-1+α)/2·2m+1+α·ηα< 推論 1任給f∈R,若C?In是對f而言的Li-Yorke混沌集合,且 則dimHC≤n-1. 定理 1在C0(In)中,存在剩余集R ?C0(In),使得對每個f∈R,若C?In對f而言是Li-Yorke混沌的,則C的Hausdorff維數dimH(C)≤n-1,并且C是第一范疇集. 證明由引理1,R是C0(In)的剩余集.根據引理2、引理3和推論1,對?f∈R,若C?In對f而言是Li-Yorke混沌的,則dimHC≤n-1. 往證對f∈R而言的Li-Yorke混沌集合C是第一范疇集即可,即只需證明每一個 是無處稠密的[5]. 因此,對上述i1,…,is-1,is+1,…,in∈{1,2,…,M},is∈{0,1,2,…,M}有 引理 4對于任2個非負實數a、b,下面2條成立: 引理 5設Ci?Ini對fi而言是Li-Yorke混沌的,i=1,2,則C1×C2?In1+n2對f1×f2而言是Li-Yorke混沌的. 于是 故 再由引理4(ⅱ)得 于是有 從而 引理 6設Ri是Xi的剩余集,i=1,2,則R1×R2是X1×X2的剩余集,反之,若R是X1×X2的剩余集,則R一定是2個剩余集R1與R2的笛卡兒積. 且 故R1×R2是X1×X2的剩余集,類似地可證明第二個結論(略). 定理 2設C0(Ini,Ini)中存在一個剩余集Ri,使得對于每個fi∈Ri,i=1,2,若集合Ci?Ini對于fi而言是Li-Yorke混沌的,則 dimH(C1×C2)≤n-1, 且C1×C2是第一范疇集. 證明因為2個疏子集的笛卡兒積是疏子集(易證),所以由命題1和引理5即可證得. 致謝嶺南師范學院重點學科項目(1171518004)對本文給予了資助,本文的提出與完成得到了導師熊金城和左再思教授的精心指導和幫助,謹致謝意.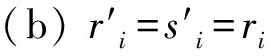
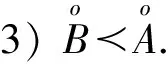
2 n維情形
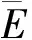
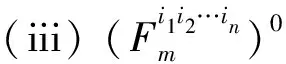
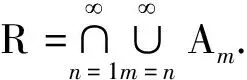
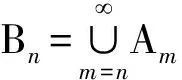
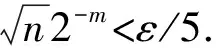

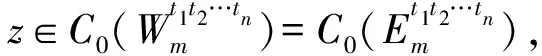
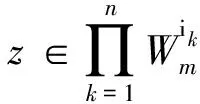

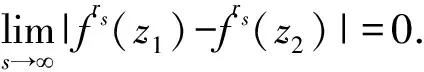
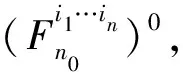
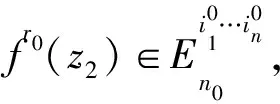
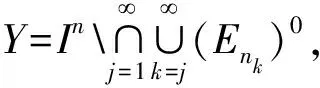
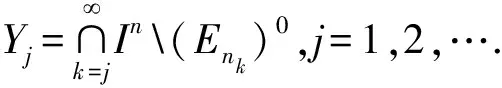
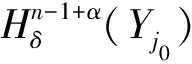

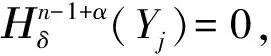
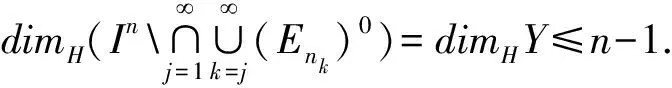
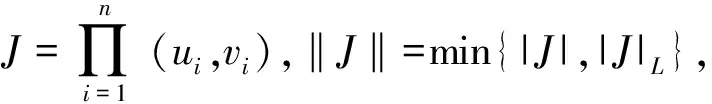
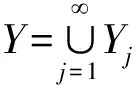
3 n維笛卡爾積情形