光電跟蹤平臺脫靶量滯后補償方法

呂明明,侯潤民,柯于峰,侯遠龍

(南京理工大學機械工程學院,210094,南京)

光電跟蹤平臺通常利用可見光或紅外圖像跟蹤器及伺服控制系統,來實現對目標的自動跟蹤[1],廣泛應用在火控、制導、靶場測試和激光通信等領域[2]。圖像跟蹤器根據所采集圖像來計算目標相對視軸的偏差,即脫靶量,并結合光電平臺的測角或測速傳感器計算目標實際位置和速度。伺服控制系統以此來控制光電平臺機構往偏差減小的方向運動,使目標始終處于視場中央。圖像跟蹤器在計算脫靶量時,需要經過圖像信號的建立和處理、由跟蹤算法提取目標位置以及信號傳輸等環節,因此脫靶量輸出往往滯后于目標實際成像時間[3]。光電跟蹤平臺的主要任務就是捕捉和跟蹤目標,而脫靶量的滯后會引起系統的超調和振蕩,降低目標跟蹤的精度,甚至導致目標捕捉和跟蹤的失敗。

由脫靶量的產生機理及處理過程可知,解決其滯后問題可以從以下3方面考慮:提高圖像采集幀頻,減少圖像跟蹤算法運算時間,利用預測模型直接或間接估計目標位置。伺服控制系統的輸入是脫靶量與平臺位置的合成值,因此用于脫靶量滯后的預測補償分為合成前預測和合成后預測。合成前預測是指通過滯后脫靶量直接估計目標不含滯后的脫靶量,再將預測值與平臺位置合成[4-6],而合成后預測是指先人為將平臺傳感器的反饋值延遲,使其與脫靶量在時間軸上保持一致,再通過合成值進行估計伺服控制系統的輸入值[7]。

脫靶量滯后是光電跟蹤系統中不可忽視的問題,如何進行補償一直是國內外研究的熱點。文獻[4]利用線性Pade逼近分析光電成像傳感器的純延遲,并采用卡爾曼濾波的多步預測法來補償脫靶量滯后。文獻[5]提出自適應卡爾曼濾波算法的模型,用其估計目標角速度,并前饋到速度回路,實現光電跟蹤平臺的復合控制。文獻[6]針對光電平臺跟蹤器延遲,采用基于自適應最小均方差(LMS)算法,結合圖像信息和無人機信息,實現對控制信號的有效預測。文獻[8]建立基于魯棒H∞濾波算法的“當前”統計模型,解決圖像跟蹤器的脫靶量滯后和信號噪聲問題。文獻[9]提出脫靶量延遲具有不確定有界時變的特性,并在此基礎上利用基于統計Singer模型和H∞控制對滯后進行補償。上述文獻均采用合成前預測,而文獻[7]作為典型的合成后預測法,提出人為將光電平臺的測角傳感器信號延遲再與脫靶量合成,之后使用卡爾曼濾波進行外推,解決了脫靶量滯后問題。

非線性跟蹤微分器(NTD)是由中國科學院韓京清研究員等針對微分信號的精確提取所設計[10],可以較好地跟蹤被噪聲污染的輸入信號,同時利用積分運算提取其近似微分信號,目前已在信號濾波[11]和微分信號提取[12]等方面廣泛應用。本文在將脫靶量滯后等效為純延遲環節和采樣保持環節的串聯的基礎上,分別利用直接預測補償法和機動目標的“當前”統計模型(CSM)進行補償,其中,直接預測補償法估計無滯后脫靶量的前提是利用NTD提取滯后脫靶量的跟蹤及微分信號。

1 脫靶量滯后問題描述

光電跟蹤平臺的主要任務是捕捉、鎖定和跟蹤目標。光電跟蹤平臺的工作示意圖如圖1所示,其主要由圖像跟蹤器、伺服控制系統和平臺負載等構成。在自動跟蹤目標時:圖像跟蹤器通過采集的圖像計算目標脫靶量,并與平臺位置合成;伺服控制系統將合成值作為輸入信號,形成隨動控制系統,控制平臺機構往脫靶量減小的方向運動,從而讓視軸始終指向目標。

圖1 光電跟蹤平臺工作示意圖

在脫靶量計算過程中,可見光或紅外傳感器生成圖像、目標跟蹤算法運行、數據傳輸等環節都需要一定的時間,使得伺服控制系統得到的脫靶量嚴重滯后于目標當前位置,這對系統的穩定性和跟蹤精度都有著不利的影響。考慮脫靶量延遲的跟蹤系統結構圖如圖2所示,脫靶量滯后相當于在伺服控制系統的位置回路中串聯了一個純延遲環節和采樣保持環節。

θT:目標位置;θO:平臺反饋位置;τ:脫靶量滯后時間;τ0:采樣保持時間;Gp(s):位置校正環節;Gv(s):速度回路的等效傳遞函數;s:拉普拉斯變換的復變量圖2 考慮脫靶量延遲的跟蹤系統結構圖

文獻[13]在假設脫靶量滯后時間為一幀時間的前提下,進一步推導了圖像跟蹤器的幀頻與位置帶寬之間的關系,公式為

(1)

式中:fT為圖像跟蹤器幀頻;fP為位置帶寬;θ0為不考慮滯后的位置環相角裕度;θ1為引入滯后的相角裕度。由此可知,脫靶量作為伺服控制系統位置回路的誤差比較環節,其滯后嚴重影響了控制系統的相位裕度,導致系統超調量的增加和位置環最大帶寬的降低,使跟蹤系統會產生振蕩,降低了跟蹤精度,甚至會導致目標捕捉和跟蹤的失敗。

2 基于NTD和CSM的補償方法

2.1 非線性跟蹤微分器

非線性跟蹤微分器是自抗擾控制器的重要組成部分,設計的初衷是從不連續或帶有隨機噪聲的信號中提取連續信號和微分信號[12]。

令z2為信號z1的微分信號,構建系統[10]為

(2)

若式(2)的所有解(按菲利波夫意義)都有界,且滿足

(3)

那么對任意有界可測信號v(t),t∈[0,∞)和任意T>0,有微分方程

(4)

式中:x1為v的跟蹤信號;x2為x1的微分信號。x1(R,t)滿足

(5)

通過選擇適當的非線性函數f(·)和參數R,使x1(t)充分逼近輸入信號v(t),同時得到輸入信號廣義導數的一種光滑逼近信號x2(t)。NTD通過積分運算得到輸入信號的微分形式,避免了傳統差分帶來的噪聲放大效應。文獻[10]給出了NTD的嚴格數學證明。理論上,通過多個NTD的串聯,可以得到輸入信號v(t)的二階或更高階微分信號[11]。

采用不同的離散方法,NTD會有不同的形式。常用的基于歐拉法的NTD離散形式[14]為

(6)

式中:v(k)為輸入信號;h為步長,由系統運算周期決定;h0和r0分別為濾波因子和速度因子,影響NTD的濾波性能和跟蹤速度,通過設置合理的h0和r0,可以得到輸入信號v(k)的跟蹤及微分信號,通常將h0取為h的若干整數倍[14];L(Δx,x2,r0,h0)為最速綜合函數,計算式為

(7)

2.2 延遲環節補償

卡爾曼濾波是光電跟蹤平臺常用的脫靶量滯后補償方法[15-17],然而卡爾曼濾波需要假設信號動態性能及噪聲統計特性已知,但實際情況并不能完全滿足[18],限制了補償效果。本文采用直接預測法補償延遲環節,其補償原理如圖3所示。

θ:目標脫靶量;θτ:滯后脫靶量;補償后的脫靶量圖3 脫靶量滯后補償原理

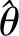
(8)

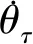
由式(8)可知,想要利用直接預測法補償滯后脫靶量,就需要首先提取滯后脫靶量的跟蹤及微分信號。直接通過差分得到的微分信號存在噪聲放大效應,并且滯后時間越小,噪聲放大越嚴重,完全可能淹沒微分信號[19]。因此,采用式(6)(7)計算滯后脫靶量的跟蹤及微分信號。

結合式(6)(8),可得出基于NTD的滯后脫靶量直接預測補償表達式為

(9)

式中:λ為預測因子,可預先設定;速度因子r0決定了跟蹤速度的快慢,r0越大跟蹤速度越快,但引入的隨機噪聲也會越大;濾波因子h0影響著濾波效果,實際上NTD的濾波效果與h0的開方成反比[20],但h0過大會增加相位的損失,因此參數調整要綜合考慮兩方面的性能。

由于目標機動性的增強,光電跟蹤平臺必須根據被跟蹤目標的變化實時調整NTD參數,以得到精準的跟蹤及微分信號,從而獲得滿意的脫靶滯后補償效果。當跟蹤信號x1和輸入信號v的間距充分小時,其微分數值充分接近[21],因此可以用間距來調整NTD的參數。進一步,為了降低信號隨機誤差的影響,采用前M個信號的間距均值來自適應調整r0和h0,計算式為

(10)

式中:M為參考的周期數;kr0和kh0分別為速度因子r0和濾波因子h0的控制增益系數,需要預先設定。

2.3 采樣保持環節補償

CSM是一種描述目標機動特性的實用模型,其假定目標在下一時刻的加速度有限,只能是在“當前”時刻加速度的鄰域內[5]。CSM的離散狀態方程為

(11)

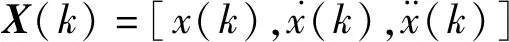
(12)

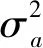
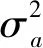
(13)

式中a+max和a-max分別為機動目標的最大正負加速度。

實際光電跟蹤平臺中,圖像跟蹤器幀頻不超過100 Hz,遠小于平臺位置反饋采樣頻率(約800 Hz)[13]。在計算相鄰兩次脫靶量期間,系統會有N個平臺傳感器的反饋數據,相當于伺服控制系統中包含一個采樣保持環節,且

(14)

式中:[·]為取整函數;T為平臺位置反饋采樣周期。

本文利用式(11)估計在采樣保持期間每個系統周期的脫靶量,其中k=1,2,…,N,此時F(k)和U(k)表達式詳見文獻[22]。

3 驗證實驗與結果

3.1 延遲環節補償實驗

為了驗證本文所提出的脫靶量滯后補償方法中延遲環節的補償效果,假定目標以θ=10sin(0.8t)做等效正弦運動,對輸入信號人為延遲并補償,進行了25 s的仿真實驗。NTD的參數設定如下:h=0.001 25 s,r0=1 000,h0=0.015,并根據式(10)實時調整r0和h0,M=5,kr0=0.1,kh0=0.1,τ=0.03 s。

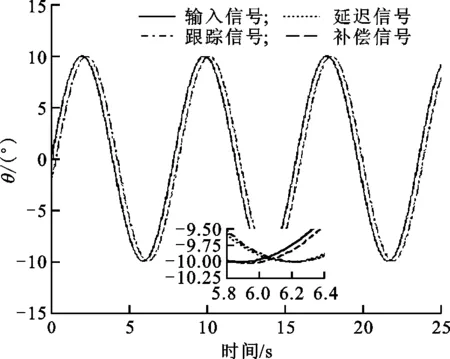
圖4 NTD跟蹤及延遲環節的補償結果

圖4是NTD跟蹤及延遲環節補償結果,可以定性地看出,跟蹤信號能夠很好地跟蹤滯后的脫靶量,直接預測法利用滯后跟蹤信號和微分信號,很好地還原了目標輸入信號,實現了延遲環節的補償。圖5是NTD跟蹤及延遲環節的誤差,通過定量分析可知,除了在初始階段因信息量不足出現較大誤差外,其余時間的跟蹤誤差范圍是[-0.24°,0.24°],脫靶量延遲環節的補償誤差范圍是[-0.15°,0.29°]。進一步,計算出跟蹤誤差的均方根誤差為0.18°,補償誤差的均方根誤差為0.21°。

圖5 NTD跟蹤及延遲環節的誤差

3.2 采樣保持環節補償實驗

將3.1節中脫靶量延遲補償后的信號作為輸入信號,進行25 s的仿真實驗。采樣保持環節補償的參數設置如下:T=0.001 25 s;采樣保持周期為0.03 s;式(12)中的機動頻率α=0.001 s-1;式(13)中的a+max=0.64 (°)/s2,a-max=-0.64 (°)/s2。

圖6是采樣保持環節的補償效果。可以看出,本文方法在采樣保持期間,很好地跟蹤了輸入信號,能夠符合目標的機動規律。圖7是采樣保持環節的補償誤差,可定量分析出采樣保持環節的補償誤差范圍為[-0.54°,0.65°],均方根誤差為0.16°。

圖6 采樣保持環節的補償效果

圖7 采樣保持環節的補償誤差

3.3 綜合補償實驗

以某型光電跟蹤平臺的高低方向進行實驗,模型結構如圖2所示,其中位置校正環節Gp(s)和速度回路等效傳遞函數Gv(s)分別為

(15)

(16)

采用基于卡爾曼濾波(Kalman)和基于自適應LMS的補償方法,與本文提出的基于非線性跟蹤微分器與“當前”統計模型的補償方法(NTD-CSM)進行對比,單位階躍響應的超調量和調節時間的對比如表1所示,單位階躍響應前3 s的曲線如圖8所示。可以看出:3種方法的調節時間相差不多,體現了光電跟蹤平臺在目標出現時快速準確的捕捉性能,NTD-CSM補償法階躍響應基本無超調,遠小于Kalman和LMS兩種方法。

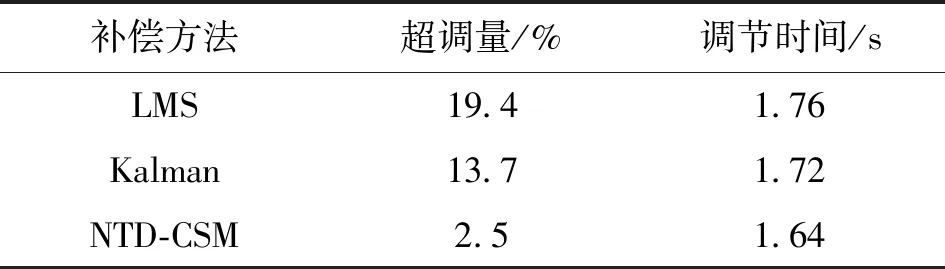
表1 單位階躍響應的結果對比

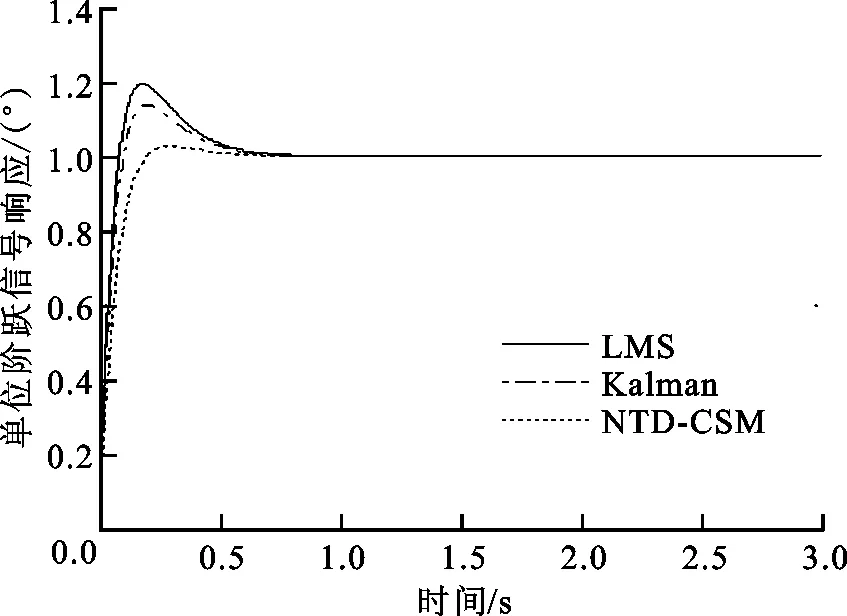
圖8 3種方法單位階躍響應曲線的比較

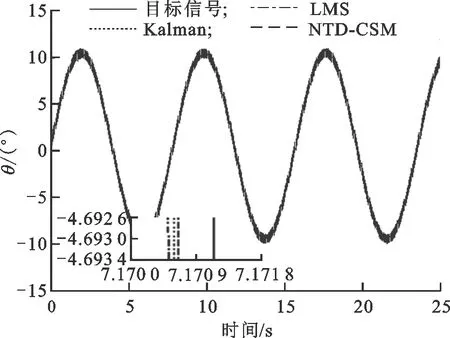
圖9 3種方法目標跟蹤曲線的比較

為驗證所設計的脫靶量滯后補償方法在目標跟蹤上的表現,仍在該平臺上假定目標以θ=10sin(0.8t)做等效正弦運動,并加入幅值為1°的隨機噪聲,同樣進行了25 s仿真實驗。圖9是3種方法的目標跟蹤曲線,可以看出,LMS的誤差范圍為[-0.44°,0.52°],Kalman的誤差范圍為[-0.49°,0.58°],NTD-CSM的誤差范圍為[-0.33°,0.47°]。圖10給出了3種方法的均方根誤差曲線,為了突出比較結果,只取前2 s的均方根誤差數據繪制曲線,可以明顯看出,NTD-CSM的跟蹤精度優于Kalman和LMS的。

圖10 3種方法均方根誤差曲線的比較

4 結 論

(1)本文提出了一種用于解決光電跟蹤平臺中目標脫靶量滯后的補償方法。根據脫靶量滯后可以等效為純延遲環節和采樣保持環節,分別采用非線性跟蹤微分器和機動目標“當前”統計模型進行補償。

(2)借助非線性跟蹤微分器獲取脫靶量滯后信號的跟蹤信號和微分信號,并采用直接預測補償法進行延遲環節的補償。由實驗可知,跟蹤信號及補償信號的均方根誤差分別為0.18°和0.21°。

(3)建立機動目標“當前”統計模型的離散狀態方程,并采用修正的瑞利分布描述加速度的“當前”概率密度,從而實現采樣保持環節的補償。實驗分析表明,采樣保持環節補償的均方根誤差為0.16°。

(4)建立綜合補償實驗模型,對比所提方法與基于自適應方差的補償方法及基于卡爾曼濾波的補償方法。在不影響調節時間的前提下,單位階躍響應的超調量由19.4%和13.7%降低至2.5%。在實際應用中應綜合考慮超調量和調節時間。