高中數學核心素養在習題教學中的體現
☉廣西壯族自治區賀州市平桂區平桂高級中學 朱遠彰
自新課改實施以來,教育部門頒布了多項政策來促使教師在教學中重點關注學生的學科核心素養,即所有課程的設置都應涵蓋思考、體驗和表達教育.思考教育,指在學習上對學生加強引導,增強其獨立思考的能力,并反思自己的得與失;體驗教育,指在學生做題時給予一定的指導和幫助,梳理做錯的習題,歸納其中的內在規律,由此讓學生迅速掌握正確的方法,提升做題的正確率及縮減做題時間;表達教育,指在課堂教學中應留出給學生交流和探討問題的時間,鼓勵學生當眾解題,以此為范例指出解題中存在的問題.此外,還應堅持具體問題具體分析的原則,點明同一類型的題目在不同情況下的問題,哪些知識點需要寫哪些知識點不需要寫.綜上所述,培養學生的核心素養不僅要傳授正確的解題思路,還要讓學生掌握相應的解題方法.
一、核心素養內涵
(1)數學核心素養符合高中數學教學的基本規律,且有利于自身的全面發展及提高將來走向社會后適應社會的能力.尤其是在新課改的大背景下,教師不僅要讓學生掌握最基本的數學原理,還要培養他們的數學思維,提升數學素養,這對其他學科的學習也大有裨益.高中數學知識相比初中難度更大、教學任務更加繁重,對學生提出了更高的標準和要求,所以教師應將數學核心素養的培養貫徹到教學的全過程,讓學生在掌握知識的同時也能夠提升思維能力和數學素養,以便更好地應用于實踐生活中.
(2)高中數學核心素養的重要性.
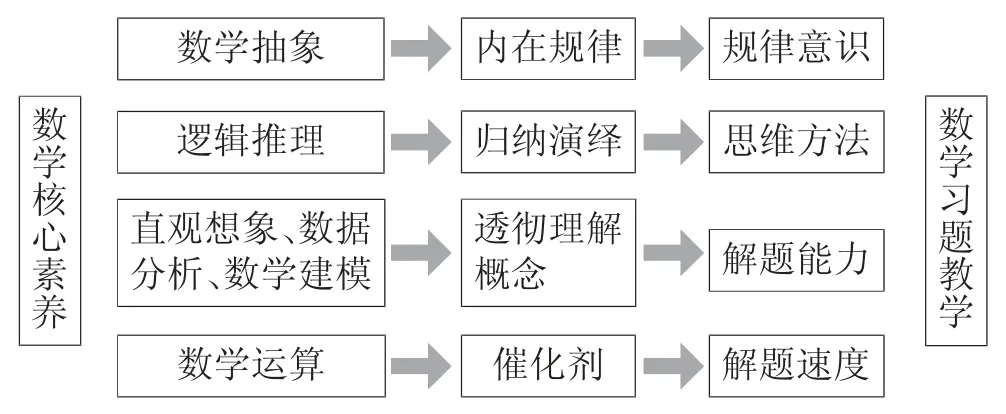
高中生應該具備的核心素養主要表現在情境和問題、思維和表達、知識和技能、交流和反思.這些素養不僅有助于提升學生的解題能力,也有助于解決日常生活中常見的問題,為將來更好、更快地適應社會打好堅實的基礎.抽象思維的利用能夠讓學生在具體問題中找到內在規律,以此形成規律意識;邏輯推理則讓學生在歸納和演繹中形成獨特的思維方法;而直觀想象、數據分析和數學建模更是從數學的角度讓學生透徹理解理論和概念,由此提高解題和做事的能力;數學運算則是解決所有習題的催化劑,加快做題速度,通過熟練的運算能力將解題思路完全地展示出來.
二、高中數學習題教學中核心素養的培養策略
(一)訓練良好的解題思維
提升學生的邏輯推理能力應該從學生的實際情況入手,采取直觀、自然的方法分析問題,從學生的視角解題,這樣得到的結果才符合學生的認知,學生才能提升邏輯思維能力,獲得更加多樣化的解題途徑.如數列中有種題型會考查證明含有數列通項公式的不等式成立,這類題目就要學生通過自己的邏輯推理能力及數學抽象能力來推斷不等式的規律,并進行歸納演繹.
例1等比數列{an}的前n 項和為Sn,已知對任意的n∈N*,點(n,Sn),均在函數y=bx+r(b>0且b≠1,b,r均為常數)的圖像上,對任意的n∈N*,當b=2時,記bn=2(log2an+1),證明:對任意的n∈N*,不等式成立.
證明:通過解題得知r=-1,bn=2(log2an+1)=2(log22n-1+1)=2n.
此時就可以應用多種思路進行解題,首先學生最常用的就是數學歸納法:
方法1:(1)當n=1 時,,因為,所以不等式成立.
(2)假設當n=k 時不等式成立,

根據(1)和(2)可知,對任意的n∈N*,不等式都成立.
方法2:也可應用放縮法.

方法3:均值定理.
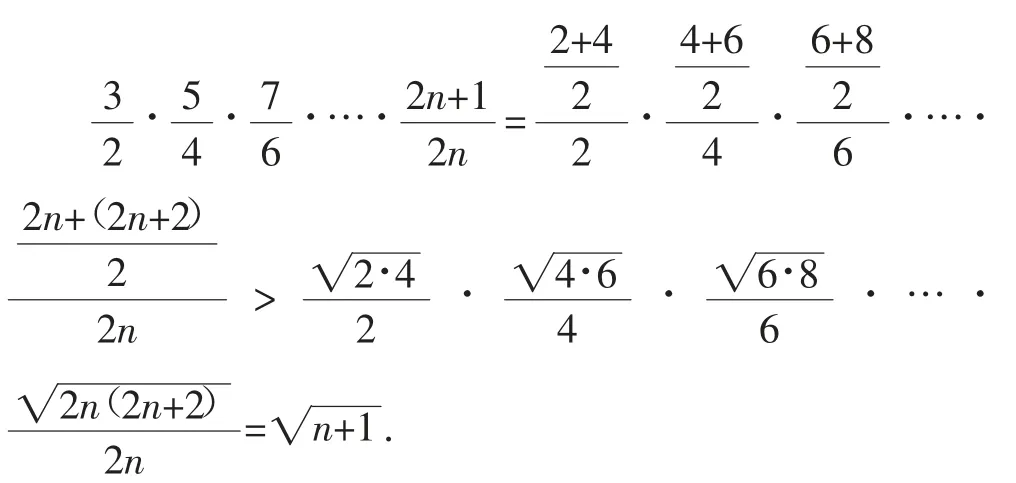
教師在教學中不應僅僅局限于公式的套用,應將點明解題思路放在首位.數學題的教學更應注重方法及其推導過程.核心素養的存在就是集體思維的整體展示,要打開學生的解題思維,不拘泥于一種解題方法,注重一題多解,找到更加多樣化的解題方法.
(二)加強過程指導,提高思維能力
數學習題的教學是師生雙方互動的過程,以教師教學作為途徑,以學生掌握做題的基本方法為目的.所以,應選擇與學生情況相符合、難度適中的數學題,這樣既不會讓學生感到沒有挑戰性,也不會產生畏難情緒.不僅能夠提升學生學習的積極性,還能優化和完善學習方法,在解題中鍛煉和提升學生自主學習的能力,保障以后開展自主學習的效果.
教師在設計活動式情境時應保持同數學習題發展方向的一致性.趣味性是活動式情境的最典型的特征,盡管其中包含游戲成分,但仍需學生具備較強的思維水平,只有這樣才能深入了解數學基本概念,保障學習效果.
(三)橫向拓展
現代思維科學的研究表明,思維是問題產生的源頭,也是推動創新的重要動力.要讓學生在學習中學會質疑權威,由此提升學生發現問題、分析問題和解決問題的能力.
例如,在開展直線和圓的位置關系這一新課程的教學中,教師在設計習題時應該秉持著從容易到困難的原則,通過階梯式的題目設置來開闊學生的思維,由此讓學生掌握基本概念和解題方法,拓寬了情境內涵的意義,由此將以往學過的、零碎的知識點串聯成一個整體.如例2,可以先由圓心到直線的距離開始入手,進而教師帶出圓與直線有幾種位置關系;再加深難度,例3通過直線與圓的位置關系來進行數形結合,求解直線的方程;教師再繼續通過綜合性習題考查學生幾何知識與代數之間的轉換.
例2(難度*)圓(x-1)2+y2=1的圓心到直線y=的距離是( ).
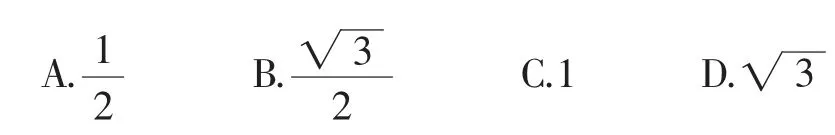
分析:選A,圓心(1,0),應用點到直線的距離公式求解.
例3(難度**)過原點的直線與圓x2+y2+4x+3=0相切,若切點在第三象限,則該直線的方程是______.
解析:設T為切點,因為圓心C(-2,0),因此CT=1,OC=2,△OCT 為直角三角形.如圖1,所以∠COT=30°.所以直線OT 的方程為

圖1
總結:
隨著新課程的改革和素質教育理念的推進,學生自主學習能力逐漸成為評價體系中的重要元素,這就對其核心素養提出了更高的要求.核心素養是高中教育的精髓,不能提升學生核心素養的教育是失敗的教育.所以在數學習題課堂教學中,教師應該樹立正確的教學理念,采用合理的教學方法.為此,筆者認為應當積極為習題教學創設趣味性的情境,從宏觀和微觀兩個角度切實解決好教師教學、學生解題中的相關問題.

