單邊核磁共振Halbach磁體結(jié)構(gòu)設(shè)計(jì)

杜海龍 王琦 周振宇 蔣川東

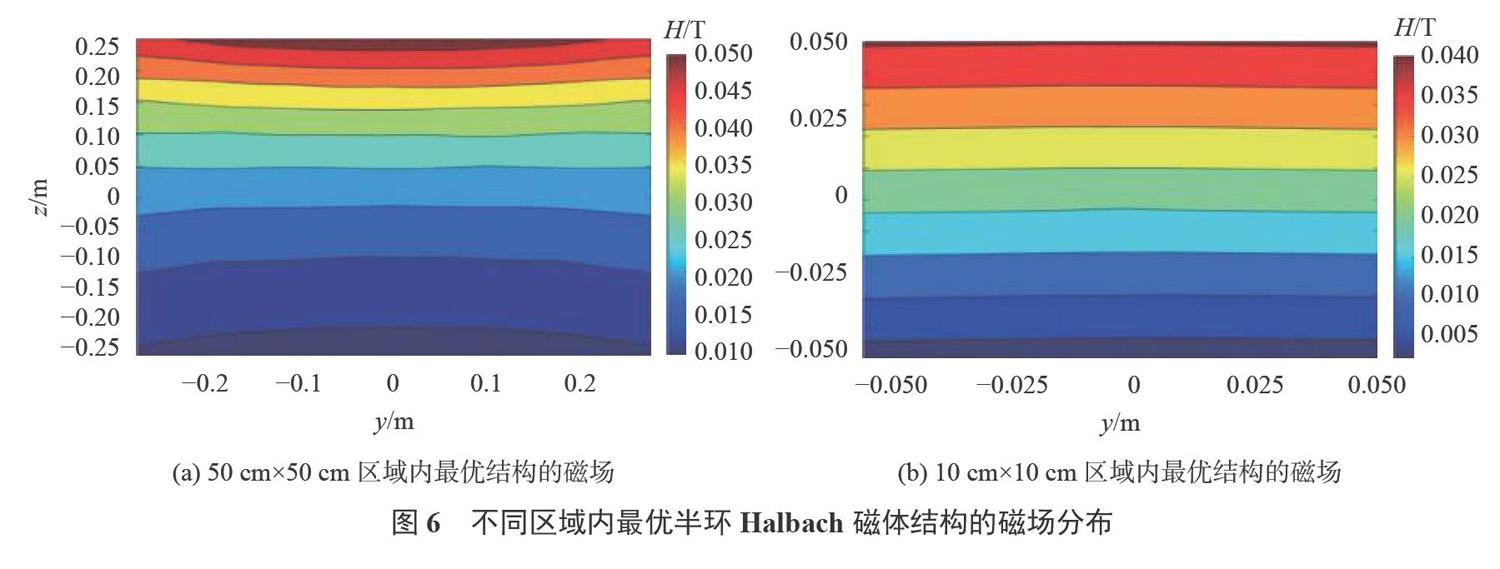
摘要：傳統(tǒng)核磁共振儀器多采用封閉式磁體結(jié)構(gòu)，導(dǎo)致儀器開(kāi)放性和便攜性差，制約其應(yīng)用范圍。為解決上述問(wèn)題，該文基于電磁場(chǎng)理論，利用二階有限元方法，研究半環(huán)形Halbach磁體的結(jié)構(gòu)設(shè)計(jì)方法，分析磁塊幾何結(jié)構(gòu)和尺寸等參數(shù)對(duì)Halbach磁體產(chǎn)生的中心場(chǎng)強(qiáng)、橫向均勻度和縱向梯度的影響。驗(yàn)證該磁體結(jié)構(gòu)無(wú)需增加線圈，即可產(chǎn)生核磁共振實(shí)驗(yàn)所需的橫向均勻縱向梯度分布的磁場(chǎng)。優(yōu)化后的單邊Halbach磁體結(jié)構(gòu)為：磁塊尺寸為0.5m×0.095m×0.095m、磁體結(jié)構(gòu)半徑為0.63m，在50cm×50cm區(qū)域得到中心場(chǎng)強(qiáng)為0.0209T，不均勻度為3.085×10^-4，梯度為0.739mT/cm的磁場(chǎng)。

關(guān)鍵詞：核磁共振儀器;Halbach磁體;有限元方法;參數(shù)優(yōu)化

中圖分類號(hào)：TM153 文獻(xiàn)標(biāo)志碼：A 文章編號(hào)：1674-5124（2019）06-0096-05

收稿日期：2018-10-29;收到修改稿日期：2018-12-03

基金項(xiàng)目：國(guó)家自然科學(xué)基金資助項(xiàng)目（41604083，41704103）

作者簡(jiǎn)介：杜海龍（1983-），男，吉林長(zhǎng)春市人，工程師，主要從事儀器與檢測(cè)方法研究。

0 引言

核磁共振作為一種高精度、無(wú)損耗的測(cè)量技術(shù)，廣泛應(yīng)用于地質(zhì)、醫(yī)學(xué)、生物和化學(xué)等領(lǐng)域[1-3]。傳統(tǒng)的核磁共振儀器中，多采用封閉式的磁體產(chǎn)生背景磁場(chǎng)，存在體積大、開(kāi)放性差等問(wèn)題[4-5]。為了增加其便攜性，同時(shí)降低儀器成本，國(guó)內(nèi)外學(xué)者開(kāi)展了對(duì)單邊主磁體結(jié)構(gòu)的研究[6-8]。K.Halbach[9]設(shè)計(jì)了直線型Halbach磁體結(jié)構(gòu)，但通常用于大型物體檢測(cè)。Blumich等[10]提出了U型磁體結(jié)構(gòu)，但是U型磁體存在磁場(chǎng)水平方向分布不均勻，導(dǎo)致縱深分辨率差的問(wèn)題。Chang Weihao等[利用兩個(gè)尺寸分別為50mmX50mmX50mm和24mmX24mmX5～的永磁體塊設(shè)計(jì)了單邊磁體結(jié)構(gòu)，但是該結(jié)構(gòu)產(chǎn)生的磁場(chǎng)在靈敏區(qū)域內(nèi)均勻度和強(qiáng)度均較低。上述單邊磁體結(jié)構(gòu)均無(wú)法直接產(chǎn)生縱向梯度磁場(chǎng)，需要額外增加梯度線圈。

為實(shí)現(xiàn)僅利用磁體即可產(chǎn)生橫向均勻、縱向梯度分布的磁場(chǎng)，本文借鑒環(huán)形Halbach磁體結(jié)構(gòu)[12]，研究了半環(huán)形Halbach磁體的原理，分析了磁體剩磁、磁體尺寸結(jié)構(gòu)參數(shù)對(duì)半環(huán)Halbach磁體結(jié)構(gòu)產(chǎn)生的中心場(chǎng)強(qiáng)、磁場(chǎng)均勻度和縱向梯度的影響，最終得到最優(yōu)的半環(huán)Halbach磁體結(jié)構(gòu)的尺寸參數(shù)。

1 Halbach磁體設(shè)計(jì)

1.1 半環(huán)型Halbach磁體原理

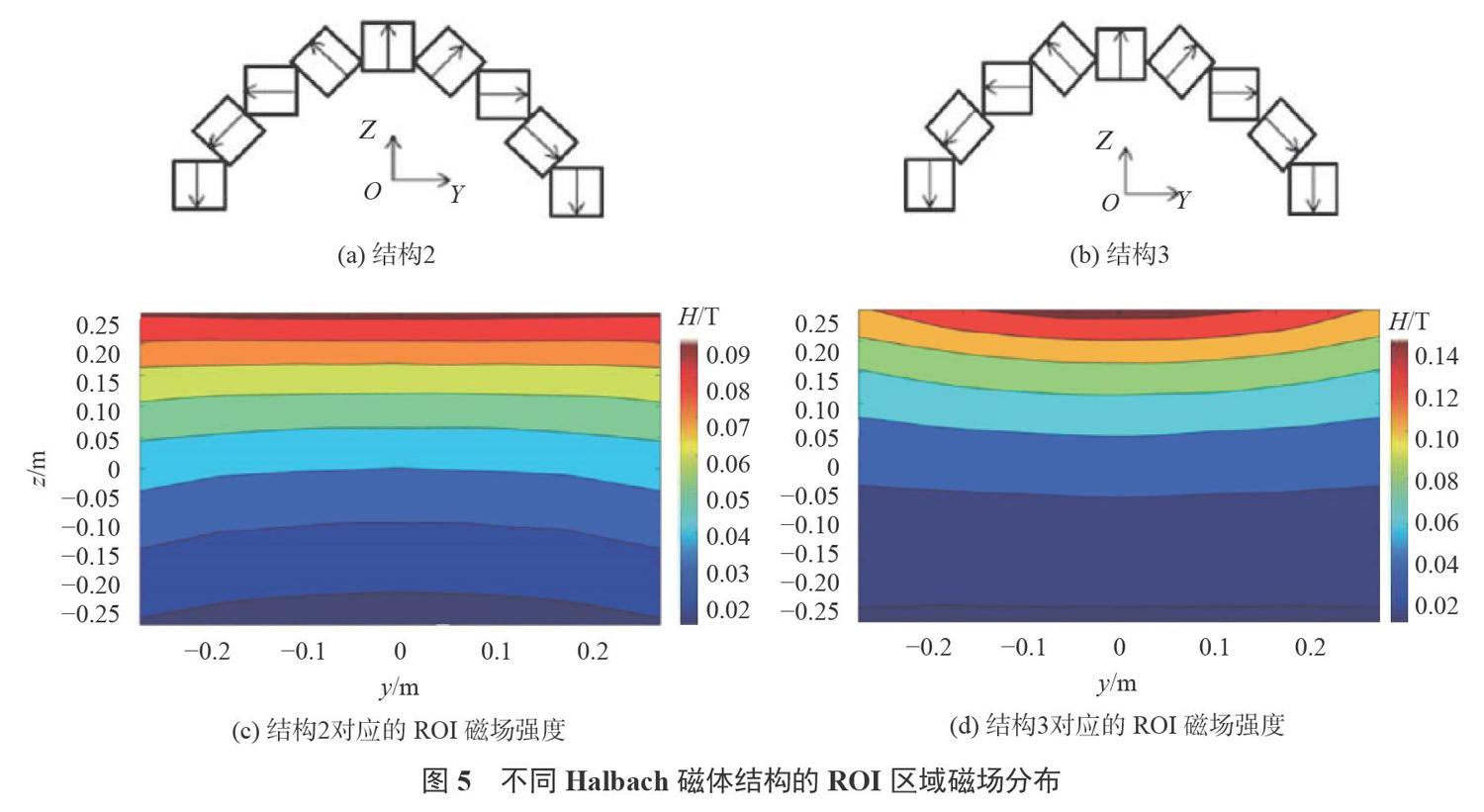
為了產(chǎn)生橫向均勻分布、縱向梯度分布的磁場(chǎng)，本文采用半環(huán)Halbach磁體結(jié)構(gòu)，如圖1所示。該磁體結(jié)構(gòu)由9個(gè)形狀、尺寸、剩磁完全相同的磁塊組成，箭頭為磁化方向。

本文以等效磁荷模型為基礎(chǔ)，采用標(biāo)量磁位法計(jì)算Halbach磁體的磁場(chǎng)。根據(jù)Maxwell方程組中的高斯定律，可得永磁體產(chǎn)生的空間任意點(diǎn)的標(biāo)量磁位φ[13-14]為式中：M——滋化強(qiáng)度;

R ——源點(diǎn)到磁場(chǎng)的距離;

ρ_ms——面磁核密度;

Ω——Halbach磁體積分區(qū)域;

Γ——磁體邊界區(qū)域。

為了得到高精度的結(jié)果，本文采用二階有限元方法[15]計(jì)算得到標(biāo)量磁位。首先采用二階四面體單元對(duì)計(jì)算區(qū)域進(jìn)行剖分，如圖2所示，則每個(gè)單元。對(duì)應(yīng)的場(chǎng)為φ^e。

單元永磁體磁場(chǎng)對(duì)應(yīng)最小泛函問(wèn)題為其中μ^e、ρ^e、σ^-e分別為磁導(dǎo)率、體磁荷密度和面磁荷密度。

對(duì)式（2）右邊求偏導(dǎo)，令其等于零：其中N_i和N_j分別為四面體的主節(jié)點(diǎn)和中間節(jié)點(diǎn)的插值函數(shù)。利用第一類邊界條件對(duì)式（3）處理后，即得到任意場(chǎng)點(diǎn)處的標(biāo)量磁位φ，將其代入H=-▽?duì)罩校纯傻玫絾芜匟albach磁場(chǎng)強(qiáng)度。

1.2 結(jié)構(gòu)設(shè)計(jì)

圖1中半環(huán)型Halbach磁體結(jié)構(gòu)，保持磁體排列為橢圓軌跡服從y²/a²+z²/b²=1（a、b分別為橢圓的長(zhǎng)半徑和短半徑），設(shè)計(jì)Halbach磁體結(jié)構(gòu)1，磁體的長(zhǎng)半徑a₁=0.55m，磁塊的尺寸為0.6m×0.095m×0.095m，剩磁B₀=1.5T。經(jīng)計(jì)算，得到靈敏區(qū)域內(nèi)（ROI）為0.5m×0.5m yoz平面磁場(chǎng)如圖3所示。可以看出，其中心場(chǎng)強(qiáng)0.04T，左右兩邊的場(chǎng)強(qiáng)明顯大于中間區(qū)域，磁場(chǎng)等位線呈上凸趨勢(shì)，磁場(chǎng)橫向均勻度較差，縱向呈梯度分布。因此本文將進(jìn)一步研究磁塊幾何結(jié)構(gòu)和磁塊尺寸等參數(shù)對(duì)中心磁場(chǎng)分布的影響。

2 影響因素和參數(shù)優(yōu)化

本節(jié)通過(guò)研究磁塊幾何結(jié)構(gòu)和尺寸等參數(shù)對(duì)Halbach磁體所產(chǎn)生磁場(chǎng)的3個(gè)主要參數(shù)（中心磁場(chǎng)強(qiáng)度、中心磁場(chǎng)水平方向的均勻度和中心磁場(chǎng)垂直方向的梯度）的影響規(guī)律，實(shí)現(xiàn)固定ROI區(qū)域半環(huán)Halbach磁體結(jié)構(gòu)的參數(shù)優(yōu)化設(shè)計(jì)。

2.1 中心磁場(chǎng)強(qiáng)度

以1.2節(jié)中的結(jié)構(gòu)尺寸為例，計(jì)算了磁體半徑和磁塊尺寸不變，不同剩磁Bo對(duì)應(yīng)的中心場(chǎng)強(qiáng)如圖4（a）所示。可以看出，中心場(chǎng)強(qiáng)隨剩磁的增大而增大，且呈現(xiàn)準(zhǔn)線性規(guī)律。當(dāng)B₀從1.0T變化至2.0T時(shí)，H從0.027 T增大至0.055T。圖4（b）給出了中心場(chǎng)強(qiáng)隨Halbach磁體結(jié)構(gòu)半徑的變化規(guī)律，可以看出中心場(chǎng)強(qiáng)隨著半徑的增大按指數(shù)趨勢(shì)減小。圖4（c）和圖4（d）給出了剩磁和結(jié)構(gòu)半徑保持不變，不同磁塊寬度和長(zhǎng)度對(duì)應(yīng)的中心場(chǎng)強(qiáng)。可以得出，隨著磁塊長(zhǎng)度和寬度的增加，中心場(chǎng)強(qiáng)均呈現(xiàn)增加規(guī)律。