汽車衡秤面防滑紋對稱重穩定性的影響研究

賴朝暉　楊曉翔　姚進輝　賴征創

摘要：選取汽車衡秤面周期分布的不同防滑紋類型為研究對象，考慮輪胎的包絡特性的條件下分別建立其等效路面高度曲線，研究其對運動車輛的激勵作用。建立1/4車輛振動模型，利用輪胎包絡特性的半經驗方法得到鋼板防滑秤面的等效高度曲線，采用輪胎包絡特性的面接觸模型得到條紋防滑秤面的有效路形，并通過Matlab/Simulink仿真，得出不同類型防滑紋的秤面對車輛激勵力的變化曲線。結果表明：對于鋼板防滑，當激勵頻率小于共振頻率時，車輛行駛速度越小，產生的激勵力越小;當激勵頻率大于共振頻率時，車輛行駛速度越大，產生的激勵力越小。鋼板間凈距小于輪印長度時，間距越小，秤面等效高度曲線波動幅度越小，但接近共振時會引起秤面激勵力的增大。對于條紋防滑，條紋與輪胎承載面的接觸面積變化越小，變化速率越慢，秤面對車輛的周期激勵力就越小。

關鍵詞：輪胎包絡特性;稱重穩定性;振動分析;防滑紋;貨車ETC

中圖分類號：TH823;O321 文獻標志碼：A 文章編號：1674-5124（2019）08-0118-06

收稿日期：2018-08-14;收到修改稿日期：2018-09-07

基金項目：國家重大科學儀器設備開發專項（2011YQ090009）

作者簡介：賴朝暉（1989-），男，福建龍巖市人，碩士研究生，專業方向為動態稱重系統的開發。

通信作者：楊曉翔（1963-），男，內蒙古赤峰市人，教授，博士生導師，研究方向為計算力學及其工程應用。

0 引言

動態汽車衡計重收費系統現已廣泛應用于高速公路收費站，精度較低、防作弊效果差的軸重式動態汽車衡已逐步被稱量精度更高的軸組式及整車式動態汽車衡所取代[1]。近幾年，我國各省、市、自治區加強ETC車道基礎設施建設，ETC模式的貨車計重收費與人工半自動化收費方式相比大大提高了貨車的放行效率，緩解了車輛的擁堵問題[2]。然而，當前我國ETC車道僅局限于客車，對以計重方式收費的貨車尚未實施ETC[3]。現有的動態稱重技術（weighing in motion，WIM），車輛計重有兩種模式，一種是“一桿一車”計重模式，一種是“整車連續跟車”計重模式;其中，連續跟車計重技術能滿足快速稱重，快速通行的需要[4]。

連續跟車的動態稱重技術，相較于靜態稱重，還要考慮車輛與秤臺之間的動荷載，因而稱量的精度遠不如靜態秤。馮秀麗等[5]對隨機路面與汽車動荷載間的關系進行了理論分析與計算機仿真，研究了路面不平度、汽車行駛速度對動態稱重結果的影響，為進一步提高汽車衡動態稱重的精度提供了理論依據。李斌[6]研究了速度與加速度對動態稱重系統的影響，將汽車振動模型進行簡化，在給定路況下不同速度的動荷載進行仿真，得到不同速度和加速度對稱重精度影響的一般規律。

秤臺表面防滑類型主要有周期分布的花紋鋼板或防滑條紋兩種[7]。不停車收費的計重系統，車輛保持相對較快的速度通過秤臺，稱重傳感器取樣時間短，要求相對穩定的稱重數據。而秤面防滑紋將對行駛中的車輛產生周期性的干擾力，引起車輛的上下振動。車輛振動產生的低頻干擾使傳感器的稱重數值發生波動，影響稱重信號的穩定性，造成電信號采集區間過度分散，進而影響稱重精度。本文從不同類型的秤面防滑類型來分析其對行駛車輛的激勵響應規律，為秤面防滑的設計和減輕車輛的稱重波動提供理論依據。

1 輪胎的濾波效應與等效路面高度

1.1 輪胎的濾波效應

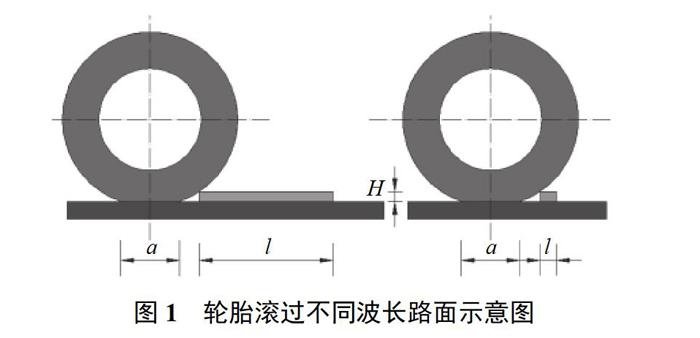
當輪胎遇到波長比接地印痕的長度還長的路面輸入時，輪胎可以看作是受到點作用力激勵的彈簧阻尼系統;當地面的激勵比接地印痕的長度小時，輪胎表現為包絡特性，即輪胎遇到路面的瞬時沖擊時，吸收或衰減該沖擊的能力，并減小了傳遞給車輛的能量[8]。如圖1所示，當路面凸臺波長滿足l>a時，輪心將隨著輪胎滾動上升的高度為H;而當l

1.2 等效路面高度的建立

因為輪胎的靜態垂直剛度隨載荷變化很小，可將輪胎在不同位置上的實際靜態垂直剛度簡化為平路面上的靜態垂直剛度，設輪胎軸高不變時，等效路面高度[9]可表示為

式中：F_z——軸高固定時輪心處的垂直力;

F_z0——平路面上輪心處的垂直力;

K_z0——平路面上輪胎靜態垂直剛度。

在低速運動下，輪胎的一般特性隨運動過程僅有細微變化a由式（1）可知，在給定等效路面高度變化的條件下，可求出運動輪胎輪心所受的垂直力變化。Bandel和Monguzzi[11]提出了一種研究輪胎包絡特性的半經驗方法，把輪胎在不同路面的響應分解成基本曲線的疊加，如半余弦曲線[12]。

2 焊接防滑鋼板周期支承振動

當秤面采用焊接方塊防滑鋼板時，如圖2所示，一般情況下，秤面鋼板長度或鋼板凈間距大于輪印長度，輪胎印痕落在平整秤面上時，等效路面高度等于秤面高度。由于車輛在秤面行駛速度較低，秤面激勵頻率較低，表現為車身的振動[12]，可用兩自由度系統模型。建立具有2個自由度的1/4汽車振動模型[5]，只考慮車身與輪胎的垂直振動，振動模型如圖3所示。圖中m₂、m₁分別為汽車本身的質量、輪胎和軸的總質量;k₂、c₂分別為汽車懸架剛度及阻尼;k₁、c₁分別為輪胎豎向剛度及阻尼;q為等效路面高度;x₁、x₂分別為輪胎與軸的垂直位移及汽車懸架的垂直位移。

2.1 等幅值的等效路面高度周期激勵

車輪滾動越過鋼板凸臺時，考慮輪胎的包絡特性，基本曲線取余弦曲線，取輪胎與凸臺接觸為曲線起點。如圖4所示，設凸臺長度為l，凸臺凈距為s，且滿足l>2AB，s>2DE，則等效路面曲線高度的變化幅值與秤面高度變化幅值一致。設車輪水平行駛速度不變，其速度設為v_x，軸重F_G，則輪胎接地印痕半長為

基本曲線半長為a=AB+DE，且有：

令基本曲線為

等效路面曲線為

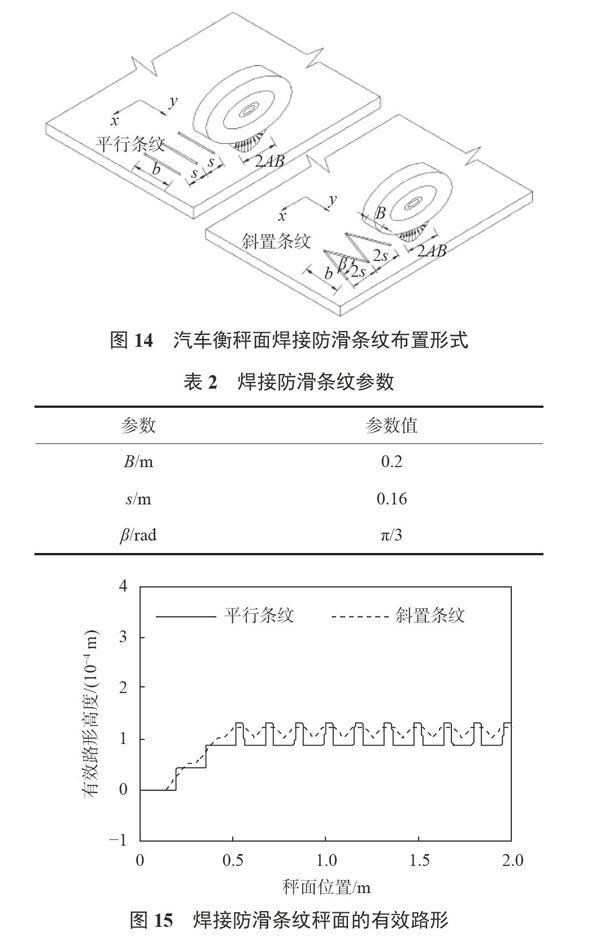
l+DE-AB≤x

考慮動態汽車衡過秤速度v_x=2m/s，振動參數如表1[5]所示。

設防滑板高度H=4mm，輪胎半徑R=635mm，l=0.8m，s=0.5m，根據式（5）可得秤面激勵的等效路面高度，如圖5所示。

相關參數代入二自由度運動微分方程[5]，可得秤面對輪胎的周期支承激勵力變化曲線如圖6和圖7所示。該振動系統一階頻率1.9HZ，振型[1，2.68]，二階頻率11.9Hz，振型[1，-0.044]。從圖6可知，秤面對車輛激勵力幅值的最大值與最小值的絕對值并不相等，不同車身質量的振動激勵力大小并無明顯規律，這是因為車身質量越大，輪胎與地面接觸面長度越大，輪胎包絡效應越明顯。從圖7可以看出，當速度為2m/s時，激勵頻率為1.5Hz，波動荷載約為車輛質量的5.4%;當速度為1m/s時，激勵頻率為0.8Hz，波動荷載約為車輛質量的3.2%。激勵頻率小于共振頻率1.9Hz時，車輛行駛速度越小，產生的波動荷載越小。在車輛行駛速度為2.47m/s的條件下，激勵頻率等于共振頻率1.9Hz，經計算對比可知波動荷載最大，約為車輛質量的18%。同樣，可以驗證激勵頻率大于共振頻率1.9Hz時，車輛行駛速度越大，產生的波動荷載越小。

2.2 不等幅值的等效路面高度周期激勵

當鋼板滿足l>2AB，s<2DE，如圖8所示，則等效路面曲線應視為基本曲線的疊加，如圖9所示，基本曲線非疊加區域如前所述，為使疊加區域滿足連續性條件，可設為曲線按如下公式進行疊加：

y=H·（cosα·sin²β+cosβ·sin²α）（6）

疊加后的曲線作為等效路面高度曲線，其最高點與原路面起伏的最高點高度相同，而最低點將高于原路面最低點，將這種曲線稱為不等幅值的等效路面高度曲線。

當l=0.8m，s=0.2m時，等效路面高度如圖10所示。在表1所示參數下，令v_x=2m/s，秤面對輪胎的周期支承激勵力變化曲線如圖11和圖12所示。從圖11可以看出，當l=0.8m，s=0.2m時，秤面對系統的激勵頻率為2Hz，接近系統一階頻率，振動荷載幅值約為車輛質量的6.4%，顯著大于l=1.2m和l=0.5m兩種情況。當l=0.8m，s=0.25m時，秤面對系統的激勵頻率為1.9Hz，引起共振，振動荷載幅值約為車輛質量的8.6%，如圖12所示。防滑板間距小于共振間距時，等效路面高度波動幅度減小，振動產生的波動荷載也減小。當鋼板間距大于共振時的間距情況下，等效路面高度波動幅度大于共振時的幅度，但是秤面激勵荷載并不必然大于共振時的荷載。當間距繼續增大時，將滿足等幅值等效路面高度的條件，對比圖7可知，當s=0.5m時，秤面激勵荷載仍小于共振時的激勵荷載。

3 焊接防滑條紋周期支承振動

車輪滾動越過微小凸紋時，如圖13所示，微小凸紋對輪胎表現為全過程的包絡特性，在輪胎的濾波效應下，輪輞豎向運動曲線變化幅度小于相應地面起伏變化幅度。設輪胎滾動過程中，接地印跡長度不變，采用輪胎包絡特性的面接觸模型[13]，輪胎垂直方向均布剛度為式中：AB——輪胎接地印痕半長;

B——輪胎胎面接地寬度。

設真實路形為q（x，y），則有效路形：

焊接防滑條紋布置形式如圖14所示，設條紋高度和寬度均為4mm，輪胎行駛在防滑條紋的中間位置，且輪胎胎面接地寬度B小于條紋寬度b，則在表2所給參數下，有效路形如圖巧所示。

將有效路形代入1/4汽車振動模型，得到秤面激勵力曲線如圖16和圖17所示。由圖16可知，對于平行防滑條紋，車輛輪胎滾過條紋時，形成瞬時沖擊荷載，當速度為2m/s時，波動荷載幅度約為車輛質量的0.32%;當速度為1m/s時，波動荷載幅度約為車輛質量的0.21%。可見車輛行駛速度越大，秤面激勵力越大。由圖17可知，斜置條紋最大波動荷載約為車輛質量的0.14%，與平行條紋比較，斜置條紋秤面有效路形高度和激勵力都較為平緩。與圖7相比較可知，焊接防滑條紋對車輛的激勵力顯著小于焊接防滑鋼板。

若防滑條紋布置寬度小于輪胎寬度，即滿足b

4 結束語

本研究對動態汽車衡最主要的兩種防滑方式分別進行周期支承振動的激勵力變化分析，得出的主要結論如下：

1）對于焊接防滑鋼板，根據前文中所給的參數的計算結果，當鋼板間凈距大于輪印長度時，在車輛行駛速度為2.47m/s的條件下，激勵頻率等于共振頻率，波動荷載最大，約為車輛質量的18%。當激勵頻率小于共振頻率時，車輛行駛速度越小，產生的波動荷載越小，如當車輛行駛速度為2m/s時，激勵頻率為1.5Hz，波動荷載約為車輛質量的5.4%;當速度為1m/s時，激勵頻率為0.8Hz，波動荷載約為車輛質量的3.2%。同樣可以驗證當激勵頻率大于共振頻率時，車輛行駛速度越大，產生的波動荷載越小。當鋼板間凈距小于輪印長度時，間距越小，秤面等效高度曲線波動幅度越小，但接近共振時會引起秤面激勵力的增大，共振條件下約為車輛質量的8.6%。

2）對于焊接條紋防滑，車輛輪胎滾過平行條紋時，會形成瞬時沖擊荷載，在前文給定的參數條件下，當速度為1m/s時，波動荷載幅度約為車輛質量的0.21%;當速度為2m/s時，波動荷載幅度約為車輛質量的0.32%。可知，激勵頻率大于一階共振頻率時，速度越大，秤面激勵力越大。而斜置條紋秤面有效路形高度變化幅度較小，產生的秤面激勵力也較小，最大波動荷載約為車輛質量的0.14%，激勵力波動較為平緩。

3）秤面周期分布的防滑紋對車輛產生的波動

（下轉第129頁）（上接第123頁）激勵力將造成稱重信號的小幅度跳動，影響連續不停車收費系統的稱重穩定性，進而影響稱重精度。因此，在設計防滑條紋時，應合理考慮條紋的尺寸大小和布置方式，避免對車輛形成共振，如用焊接防滑條紋代替防滑鋼板，斜置條紋代替平行條紋，還應盡量減小條紋與輪胎承載面接觸面積的變化和變化速率，如適當減小條紋橫向布置寬度。此外，在滿足秤面防滑性和耐磨性要求的前提下，秤面也可采用涂裝防滑涂料，或采用拉毛、壓痕或刻痕等防滑處理的混凝土面板結構。

參考文獻

[1]朱國偉，范長江，周驥，等.淺談動態汽車衡發展史[J].中國交通信息化2016（7）：98-99.

[2]張劍勇，周尚儒，楊軍.ETC模式貨車計重收費系統設計[J].中國測試，2016，42（7）：84-87.

[3]雷茂錦，余緒金，程旻瑞.貨車ETC技術的研究與應用[J].中國交通信息化2017（3）：84-86.

[4]孫曉寧.全車型貨車ETC技術在河北京張高速公路中的應用[J].中國交通信息化2018（5）：114-115.

[5]馮秀麗，李曉林，楊洪扣.路面不平度與汽車速度對動態汽車衡稱重的影響[J].中國科技論文，2012，7（11）：857-861.

[6]李斌.速度與加速度對動態稱重系統的影響[J].山西電子技術，2015（1）：43-45.

[7]王同良，冷曉飛，張衛國，等.防滑涂料在汽車衡中的應用[J].中國涂料，2016，31（5）：58-63.

[8]GENT AN，WALTER J D.輪胎理論與技術[M].危銀濤，李勇，馮希金，等，譯.北京：清華大學出版社，2013：325-327.

[9]郭孔輝，章新杰，吳海東，等.形態學濾波在輪胎包容特性中的應用[J].吉林大學學報（工學版），2009（A1）：1-4.

[10]ALKAN V，KARAMIHAS S，ANLAS G.Experimentalanalysis of tyre-enveloping characteristics at low speed[J].Vehicle System Dynamics，2009，47（5）：575-587.

[11]BANDEL P，MONGUZZI C.Simulation model of thedynamic behavior of a tire running over an obstacle[J].TireScience and Technology，1988，16（2）：62-77.

[12]吳海東.不平路面中頻激勵輪胎動態特性研究[D].長春：吉林大學，2007.

[13]郭孔輝，劉青，丁國峰.輪胎包容特性分析及其在汽車振動系統建模中的應用[J].汽車工程，1999，21（2）：65-71.

（編輯：莫婕）