電場強度求解的若干思想方法

廣東

(作者單位：廣東省中山市中山紀念中學)

梳理電場強度求解的若干思想方法的共性和特性

《高考大綱》中對于電場強度是Ⅱ級要求，要求能理解與應用，進行分析與綜合。高考題中對電場強度的求解靈活多變，側重于考查物理思維和物理方法，具有一定的區分度和難度，考查了《考試大綱》所列五種能力的前四種，即理解、推理、分析與綜合、應用數學處理物理問題能力。本文就電場強度的求解方法和物理思想進行原理闡述和點評，指出方法的共性和特性，以期能更好地提高學生解題能力。

一、場強疊加原理、割補法

電場強度是矢量，其合成遵循平行四邊形法則。當空間同時存在多個點電荷，其產生的場強互不影響，電場中某點的場強為各個點電荷在該點場強的矢量和。通過微積分或者高斯定理可以證明推論一：半徑為R的均勻帶電球殼或球體對球外一點的場強，等效于位于球心的、電量相等的點電荷產生的場強。半徑為R的均勻帶電球殼對球殼內一點的場強為零。

【例1】一半徑為R的絕緣球殼上均勻地帶有電荷量為+Q的電荷，現在球殼上挖去半徑為r(r?R)的一個小圓孔A，求剩余部分導體在球心O的場強E。

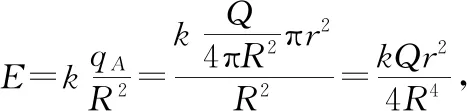
方法二：微元法與對稱思想。將球殼分成許多微元，每一組相對于球心對稱的微元產生的合場強為零，故剩余部分導體在球心的場強E與A產生的場強E1等大反向。

二、微元法、分割與累積思想

微元法、分割與累積思想是微積分的思想方法，將整體進行細分后累加，側重于突顯局部對象之間的規律，從而達到表征不規則、不直觀、條件不適用的整體對象總體特點的目的。微元法常用于以下情形：研究對象整體不適用于物理規律范圍，但若將整體分割成無限小的微小對象則適用于規律范圍，并且微元法單獨用于研究局部，能達到化“變化量”為“不變量”的作用。

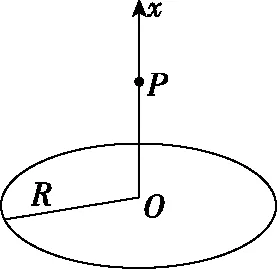
【例2】如圖1所示，均勻帶電圓環所帶電荷量為Q，半徑為R，圓心為O，P為過圓心O且垂直于圓環平面的軸上的一點，OP=L，試求圓環電荷在P點產生的場強大小E(靜電力常數為k)。

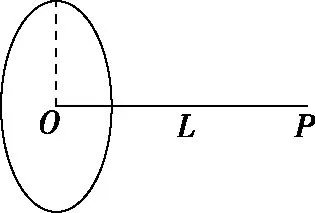
圖1

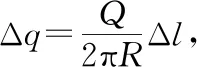
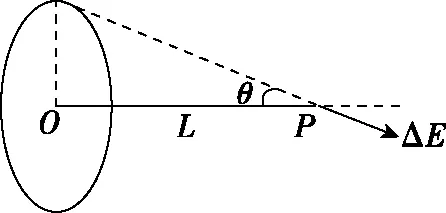
圖2

三、靜電平衡導體內部場強為零

靜電平衡時，導體是一個等勢體，導體上自由電荷不再發生移動，故導體內部合場強為零，該合場強為外部場源產生的場強和導體上感應電荷產生的場強的矢量和。

【例3】如圖3所示，半徑為R的金屬球殼A放在點電荷Q周圍，將發生靜電感應現象，球殼球心與點電荷Q的距離為r，求感應電荷在球心處的場強E(靜電力常量為k)。

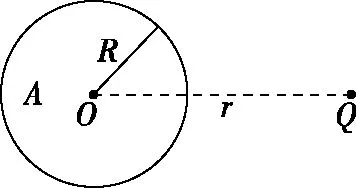
圖3

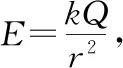
四、補償法

補償法適用于研究的場源對象為點電荷，點電荷不計大小，故可認為點電荷上所有電荷集中于一點，因此場源上的各個電荷與試探電荷的空間距離相同，距離可視為恒量，影響空間場強的因素是場源電荷量，帶電量為+Q的點電荷，可以看成是電荷量代數和為+Q的幾個電荷同處于同一點上，根據電荷間的作用是獨立的、不因第三個電荷存在而改變，可認為點電荷在外部產生的場強是由各個獨立的電荷產生的。

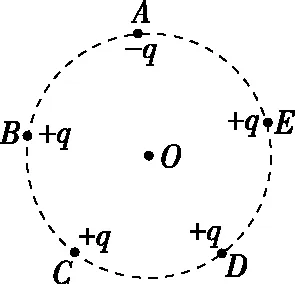
圖4

【例4】如圖4所示，A、B、C、D、E是半徑為r的圓周上等間距的五個點，在這些點上各固定一個點電荷，除A點處的電荷量為-q外，其余各點處的電荷量均為+q，則圓心O處

( )

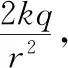
五、極限法

極限法是數學方法在物理問題中應用的一種方法。極限法側重于讓變量進行無窮大或無窮小的變化，由量變引起質變，化有限為無限，構造模型之間的對立統一關系。例如，將有限的圓形半徑這一變量變為無窮大，則無窮大圓面與無窮大平面已經是統一的。

( )

甲

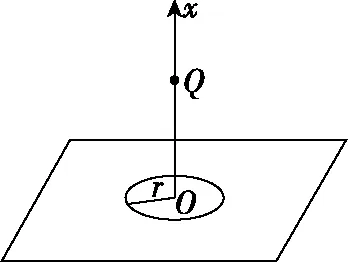
乙

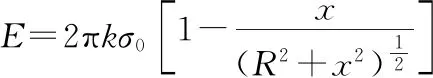
六、鏡像法

鏡像法的基本原理是靜電場邊值問題的唯一性定理，給定一組邊界條件，空間中的電場分布唯一確定。高中物理中常見的鏡像法模型對象是點電荷和無限大平面導體(或無限大相互垂直平面導體)構成的靜電平衡電場分布問題。由唯一性定理可推論，若電場的電勢分布相同，則其電場強度分布也相同。靜電平衡下的無限大平面表面的電場線與平面處處垂直，且電場分布具有對稱性，所以，可以用具有相同電場線分布的場源電荷來等效替代無限大平面導體進行求解。

【例6】如圖6所示，在無限大接地金屬板上方距板d處有一個+Q點電荷，求金屬板表面P點的場強大小(已知QP垂直于板面)。

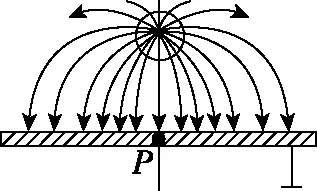
圖6

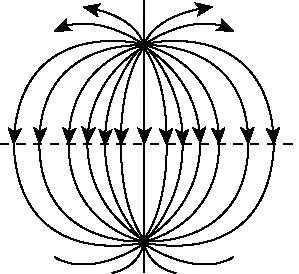
圖7

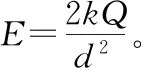
七、總結