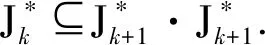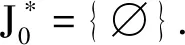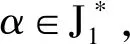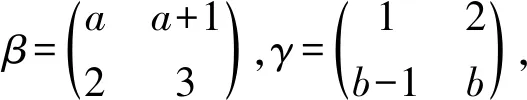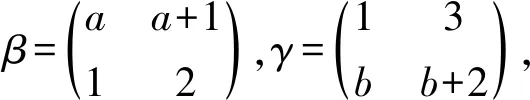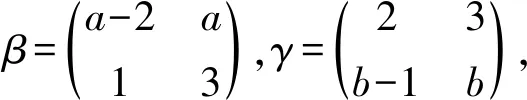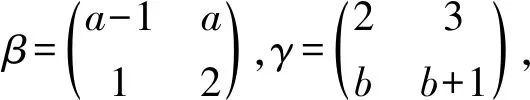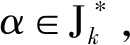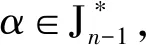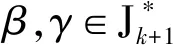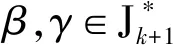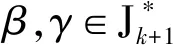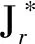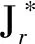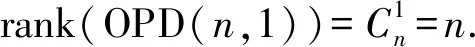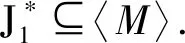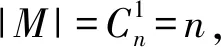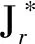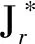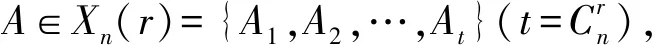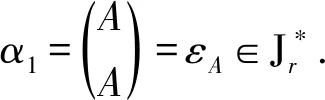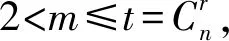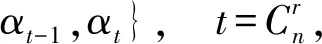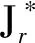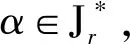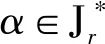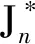半群OPD(n,r)的秩和相關秩
李曉敏, 羅永貴, 趙 平
(貴州師范大學 數(shù)學科學學院, 貴州 貴陽 550025)
1 預備知識
設[n]={1,2,…,n-1,n}(n≥3)并賦予自然數(shù)的大小序.In與Sn分別表示[n]上的對稱逆半群(即部分一一變換半群)和對稱群,SIn=InSn是[n]上的部分一一奇異變換半群.設α∈SIn,若對任意的x,y∈Dom(α),x≤y可推出xα≤yα,則稱α是部分一一保序的.記OIn為[n]上的保序有限部分一一奇異變換半群.設α∈OIn,若對任意的x,y∈Dom(α)有
|xα-yα|=|x-y|,
則稱α是保距的.令
OPDn={α∈OIn:(?x,y∈Dom(α)),
|xα-yα|=|x-y|},
則稱OPDn為[n]上的保序且保距有限部分一一奇異變換半群.記
OPD(n,r)={α∈OPDn:|Im(α)|≤r},
0≤r≤n-1,
易見OPD(n,r)是OPDn的子半群,且對任意的α∈OPD(n,r),βγ∈OPDn,均有|Im(βαγ)|≤r,即βαγ∈OPD(n,r),因而OPD(n,r)是OPDn的雙邊星理想.
通常一個有限半群S的秩定義為
rank(S)=min{|A|:A?S,〈A〉=S}.
半群S及其子半群V之間的相關秩定義為
r(S,V)=min{|A|:A?S,A∩V=?,〈A∪V〉=S},
易見r(S,S)=0.對于有限半群的秩及其相關秩的研究目前已有許多結果[1-11].文獻[1]考慮了[n]上的保序有限部分一一奇異變換半群OIn的理想
KO(n,r)={α∈OIn:|Im(α)|≤r}, 0≤r≤n-1
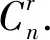
本文在文獻[1-10]的基礎上繼續(xù)考慮保序且保距部分一一奇異變換半群OPDn的雙邊星理想OPD(n,r)的秩和相關秩,證明了如下主要結果.
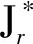
定理 2設n≥3,0≤r≤n-1,則
定理 3設n≥3,0≤l≤r≤n-1,則
設A是自然序集[n]的非空子集,符號εA表示A上的恒等變換.用?表示空變換,規(guī)定:?是保距變換,?是部分一一保序變換.設α∈OPD(n,r),用Im(α)表示α的象集,Ker(α)表示Dom(α)上的如下等價關系
Ker(α)={(x,y)∈Dom(α)×Dom(α):xα=yα}.
對任意的t∈Im(α),tα-1表示t的原象集且|tα-1|=1.若|Im(α)|=k,1≤k≤r≤n-1,則由保序性和保距性容易驗證α有如下表示法
其中,a1 |aj-ap|=|bj-bp|, 于是,令 A={a1 為敘述方便,這里引用Green*-等價關系[12].不難驗證,在半群OPD(n,r)中,L*、R*、J*有如下刻劃:對任意的α,β∈OPD(n,r)有 (α,β)∈L*?Im(α)=Im(β), (α,β)∈R*?Ker(α)=Ker(β), (α,β)∈J*?|Im(α)|=|Im(β)|. 易見L*?J*,R*?J*.記 k=0,1,2,…,r-1,r. 不難驗證OPDn具有如下包含關系的雙邊星理想鏈OPD(n,0)?OPD(n,1)?OPD(n,2)?…?OPD(n,n-2)?OPD(n,n-1)=OPDn. 定義 1[4]若對任意的A={a1 ai-ai-1=bi-bi-1, 則稱A與B同距,否則稱A與B不同距. 將Xn(r)按照同距概念進行分類.對任意的A∈Xn(r),記A的同距類為[A].進一步可證:對任意的 A={a1 必定存在 C={1 為完成定理的證明先給出若干引理與推論. 若a 情形2若a=n,注意到n≥3,則a-2≥1. 引理 2對2≤k≤r-1,3≤r≤n-1,有 其中 a1 對任意的j,p∈{1,2,…,i-1,i,i+1,…,k-1,k}有 |aj-ap|=|bj-bp|. 情形1若存在j∈{2,3,…,i-1,i,i+1,…,k-1,k},使得aj-aj-1≥3. 如果i β= γ= 如果i=j,令 如果i>j,令 情形2若存在j,p∈{2,3,…,i-1,i,i+1,…,k-1,k}且j≠p使得aj-aj-1≥2且ap-ap-1≥2,不失一般性,不妨設j 如果j 如果j β= γ= 如果j 如果i=j β= γ= 如果i 如果i β= γ= 如果i=j,令 如果i>j,令 β= γ= 若bk 如果i β= γ= 如果i=j,令 如果i>j,令 β= γ= 情形4對任意的j∈{2,3,…,i-1,i,i+1,…,k-1,k}使得aj-aj-1=1.利用保序性和保距性可知:對任意的j∈{2,3,…,i-1,i,i+1,…,k-1,k}使得bj-bj-1=1.由2≤k≤r-1,3≤r≤n-1可知k≤n-2,即k+2≤n. 如果a1≠1且b1=1,令 β= γ= 如果a1≠1且b1=2,令 如果a1≠1且3≤b1≤n,令 如果ak≠n且b1=1,令 如果ak≠n且b1≠1,令 引理 3設α,β∈OPD(n,r),若(α,β)∈J*且(α,αβ)∈J*,則(αβ,β)∈L*,(α,αβ)∈R*. 證明設α,β∈OPD(n,r),若(α,β)∈J*且(α,αβ)∈J*,則 |Im(α)|=|Im(β)|=|Im(αβ)|. 再由 Im(αβ)?Im(β), Ker(α)?Ker(αβ), 與[n]的有限性知 Im(αβ)=Im(β), Ker(α)=Ker(αβ), 即 (αβ,β)∈L*, (α,αβ)∈R*. 推論 1設自然數(shù)n≥3,則 引理 4設自然數(shù)n≥3,則 證明由引理1的證明過程易知 顯然有 rank(OPD(n,0))=1. M={α1,α2,…,αi-1,αi,αi+1,…,αn-1,αn}, 則 當i α=αiαi+1…αj-1; 當i=j時,有 α=αiαi+1…αn-1αnα1α2…αi-2αi-1; 當i>j時,有 α=αiαi+1…αn-1αnα1α2…αj-2αj-1. OPD(n,1)=〈M〉. 再結合推論1立即有 對其余的同距類也用類似的方式進行構造,可以得到集合 若|[A]|=1,則 α=εA=εIm (α). 若|[A]|≥2,則: 當i α=αiαi+1…αj-1; 當i=j時,有 α=αiαi+1…αm-1αmα1α2…αi-2αi-1; 當i>j時,有 α=αiαi+1…αm-1αmα1α2…αj-2αj-1. 因此,結合推論1與引理4,立即有 定理3的證明當l=r時,顯然有 r(OPD(n,r),OPD(n,l))=0. 當0≤l 即證得 r(OPD(n,r),OPD(n,l))= 注 1半群 OPD(n,n)=OPD(n,n-1)∪{ε[n]} rank(OPD(n,n))=n+1. 致謝貴州師范大學研究生創(chuàng)新基金(YC[2018]023)對本文給予了支持,謹致謝意.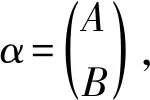
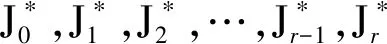
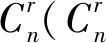
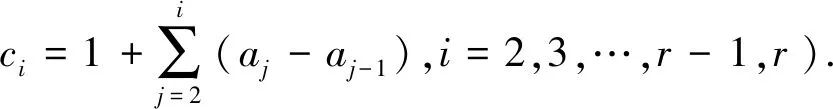
2 定理的證明