基于Excel數據建模求解及結果分析

石建國

（安徽工程大學計算機與信息學院，安徽蕪湖241000）

數據分析和處理在各領域都有重要的應用，根據數據之間的關系和實際問題的需求，建立現實問題的數學模型，通過相關軟件或設計算法并進行編程對模型進行分析和求解，以此找出解決問題的最優化方案。為此，需要借助數據處理軟件進行復雜數據的處理,常用的數據處理分析軟件有Excel、SPSS、Matlab、R等。但除Excel外，其他軟件對數據分析人員的專業技術能力要求相對較高、使用較復雜、軟件購置費較昂貴，成為使用過程中的一個瓶頸。

規劃求解問題在很多領域都有廣泛的應用，如果不用Excel求解，通過編程實現非常復雜，而且算法的準確性不易得到保證。類似的數據處理工具諸如Spss，雖然也具有較強的數據處理和分析功能，但與辦公軟件如Office或WPS兼容困難；另一種用于數值分析和計算的重要軟件Matlab雖然功能強大，但較難掌握，尤其是在算法設計和實現時需要通過對象化編程，程序執行速度較慢，而且使用成本昂貴。Excel是一款通用且簡單易學的數據處理軟件，同時具有操作簡單方便、使用廣泛和成本低等優點，常用于一些簡單的數據處理。同時，Excel也有一些實用功能可解決復雜的應用問題，但這種復雜的應用在普通教材和Excel幫助中均沒有詳細介紹。文章通過實例探討利用Excel規劃求解工具求解最優化問題的思路和方法，并對處理結果中輸出的敏感性報告進行了分析，并驗證了結論的正確性。

1 Excel數據處理及分析方法

（1）Excel提供了很多數據處理和分析方法。目前常見的應用于數據處理的方法有排序、篩選、分類匯總、合并計算及各類數據處理函數，這些數據處理方法，通過簡單學習便可熟練掌握并運用。

（2）用于數據分析的方法有規劃求解、數據透視圖表、各類圖表(如條形圖、柱形圖、散點圖、餅圖等)、描述性統計、均值推斷、概率統計、回歸分析（線性回歸、邏輯回歸和多元回歸等）、時間序列、T-test、Z-test等。其中描述性統計和概率統計方法通常用于匯總數據，其與回歸分析、T-test和Z-test統稱為傳統的統計分析方法。時間序列用于預測分析，為非傳統統計分析方法[1]。

2 線性規劃問題求解

線性規劃問題數學模型通常由變量、約束條件和目標函數3個要素組成。通過列出約束條件及目標函數，找出約束條件所表示的可行域，在可行域內求目標函數的最優解[2]。根據現實情況，從中建立數學模型一般分3個步驟：（1）根據目標影響因素確定決策變量；（2）由決策變量和目標之間的數量關系確定目標函數；（3）根據決策變量的客觀限制條件確定決策變量應滿足的約束[3]。以下以運輸問題為例來闡明Excel在線性規劃求解中的應用。

3家企業X1、X2、X3生產同一產品，其產量分別是46、22、32（單位：萬件），現要將產品運到Y1、Y2、Y3、Y44個地方，這4地的產品需求分別為27、39、20和14（單位：萬件），試確定最優化方案[4]。從產地到銷地的產品運價如下面矩陣所示：

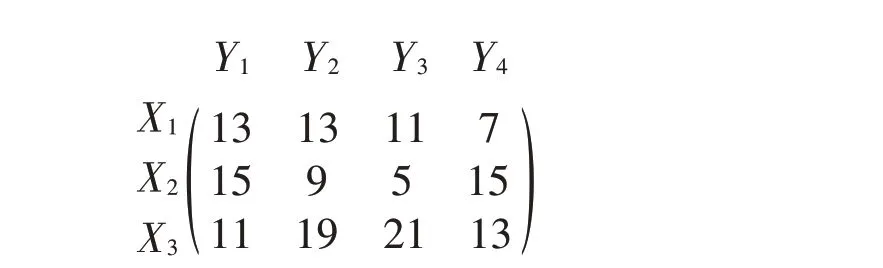
若設xij為從產地Xi到需求地Yj的產品運輸量，則該運輸問題的線性規劃模型為

min Z =13x11+13x12+11x13+7x14+15x21+9x22+5x23+15x24+11x31+19x32+21x33+13x34，將上述模型對應的數據填入Excel工作表中，如圖1所示。各單元格之間的運算關系如表1所示。

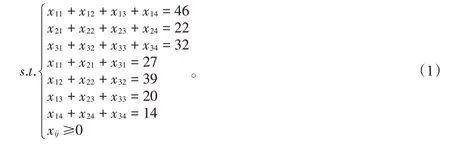
在Excel 中點擊“數據”菜單，找到“模擬分析”中的“規劃求解”選項，出現圖2“規劃求解參數”對話框。其中求解目標在工作表的B14單元格顯示，數據可動態改變的單元格范圍為$B$8：$E$10，滿足的約束條件為（1）$B$11：$E$11=$B$13：$E$13；（2）$F$8：$F$10 =$H$8：$H$10。

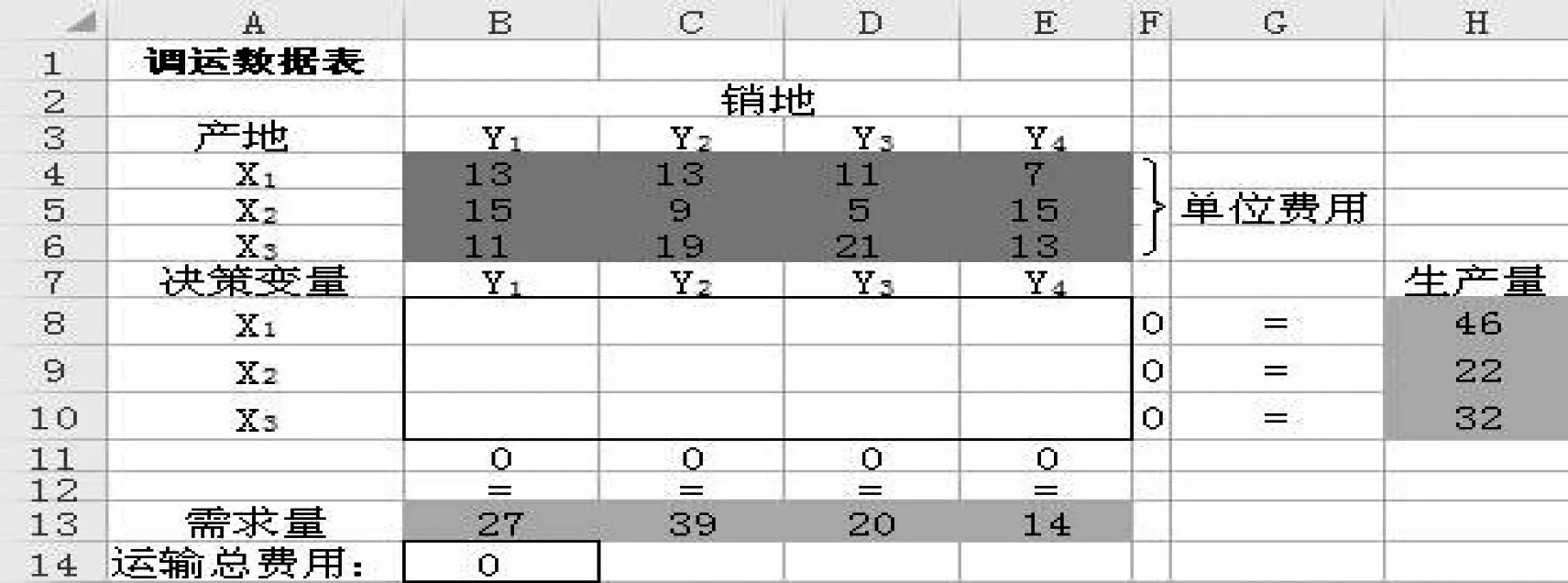
圖1 運輸問題的電子表格模型

表1 運輸問題模型中的公式設置

點擊圖2中的“求解”按鈕，在Excel中輸出的最優解如圖3所示。由圖3可知，通過單純線性規劃得出的最優化運輸方案為從X1調運32（萬件）到需求地Y2，調運14（萬件）到需求地Y4；從X2調運2（萬件）到需求地Y2，20（萬件）到需求地Y3；從X3調運27（萬件）到需求地Y1，調運5（萬件）到需求地Y2。這樣可以使得運輸費用最小為1 024（百元）。

圖2 運輸問題的規劃求解參數設置

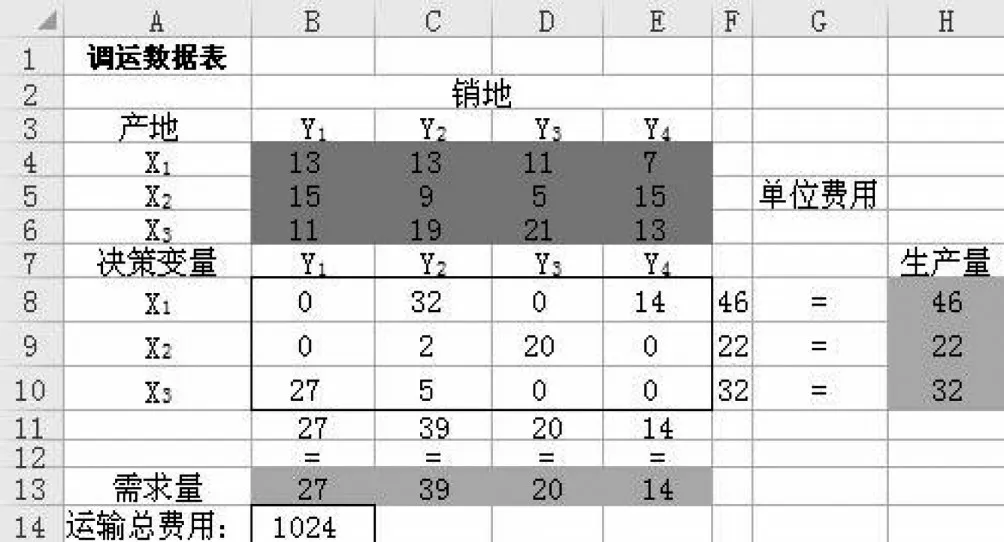
圖3 運輸問題最優方案

3 結果分析

結果分析中最重要的是敏感性報告中各項參數的分析，最重要的參數有陰影價格、遞減成本、目標式系數和允許的增減量分析。

3.1 敏感性分析的內涵及作用

所謂敏感度分析，是指對某些可能變化的因素及其對決策目標影響程度的反復分析，以揭示決策方案如何隨可變因素變化而變化[5]。實例中建立線性規劃模型所需的數據都是已知的，這些數據被稱為模型參數。但在現實應用中獲取這些模型參數并不容易，需要付出大量時間和精力，并通過實踐和檢驗才能獲得可靠的數據，有時即使投入大量時間和精力，也只能得到模型參數的粗略估計或預測值。因此，結果分析需要研究兩個問題：一是當參數中的一個或多個發生變化時，已求得的線性規劃最優解會如何變化；二是參數在什么范圍內變動，最優解能夠保持不變[6]。

敏感度分析的作用主要有兩點：（1）可了解相關因素的變動對決策方案、目標或者其他評價指標的影響程度，找到影響最優決策方案的相關因素，并進一步分析或者估算影響決策目標的不確定因素，有利于比較不同備選方案對關鍵敏感因素的影響程度，以便選擇敏感性相對較小的方案，從而減小決策風險。（2）幫助決策者掌握方案最優與最劣的可能變動范圍，通過分析把握如何采取有效控制措施，以便選取最有經濟意義的決策方案[7]。

3.2 敏感性報告輸出

在求解輸出最優化運輸方案時，點擊“規劃求解參數”界面的“求解”按鈕，顯示界面如圖4所示。

選中“報告”框中的“敏感性報告”，點擊“確定”，便可輸出“敏感性報告”，對敏感性報告中的數據進行整理，輸出結果如表2和表3所示。表2為可變單元格部分，對應于目標函數中的xij；表3為約束部分，即限制條件，對應于各地產銷量的約束限制范圍。

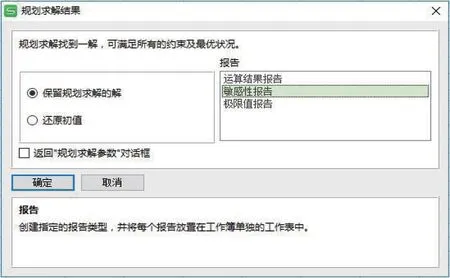
圖4 規劃求解結果界面

表2 敏感性報告之一：可變單元格部分

表3 敏感性報告之二：約束部分

3.3 參數分析

（1）可變單元格參數分析。可變單元格部分共提供5欄數據。“終值”表明問題的最優解，“遞減成本”說明降低成本的數量，“目標式系數”表示單位運價，“允許的增量”和“允許的減量”標明單位運價在“已知運價，允許增量,允許減量”之間變動，運輸方案可以不變。若超過這個范圍，運輸方案則需要變更。此范圍即為最優解的敏感度。表中“1E+30”表示無窮大，此處可以理解為大于零的任意值。若設單位運價為xij，則在本例中，的變化范圍為，則，即產地X1到銷地Y1的單位運價x11的取值范圍為。同理可得在保證運輸方案不變的前提下，各產地和銷地之間的單位運價xij的變動范圍，結果如表4所示。

表4 單位運價變動范圍

遞減成本（Reduced cost）也叫減少成本，等于相應目標函數中變量檢驗數的值[8]，是敏感性報告中的一個重要參數，是Excel輸出時目標函數中xij的系數。而對于求最大值的線性規劃而言，所有檢驗數必小于等于0；對于求最小值的線性規劃而言，所有檢驗數必大于等于0。與之對應，如果目標函數若是求最大值，則遞減成本必小于等于0。故根據遞減成本的正負就能判斷出目標函數是求最大值還是最小值。本例中目標函數是求最小運輸費用，則遞減成本必小于等于0。

同時，觀察表2 中的終值和遞減成本的對應關系，可以得出終值與其相應的遞減成本的積為0，即×Rij=0（表示變量xij的終值，Rij表示變量xij的遞減成本）。這種性質稱為最優解與遞減成本的互補松弛性[9]。據此，只要知道終值和遞減成本其中一項不為0，則可推知另一項必為0。

表2中產地和銷地之間沒有產品運輸關系的有6個。以X3→Y3為例，X3到Y3的單位運價為21（目標函數中x33的系數），如果要使X3Y3的終值不為零，即最優方案中有產地X3往銷地Y3的產品運輸，在保證最優解不變的前提下，可對表3中的R33參數進行調整，當R33的值由6減少到0時，才會出現X3Y3對應的終值不為0的結果。若其他條件不變，實例中產地X3到銷地Y3的單位運價減少到15時，從產地X3才會運送產品到Y3，這就是Excel敏感性報告中遞減成本蘊含的有價信息。

為驗證上述判斷的正確性，將產地X3到銷地Y3的單位運價改為15，運用非線性內點法重新求解一次，得到的最優解如表5所示。

由表5可知，方案更改后產地X3到銷地Y3有2萬件產品的運輸量（對應于灰色單元格數值）。將表5數據代入目標函數，與之前的最優運費相同，驗畢。

表5 單位運價變動后的最優化方案

（2）約束部分參數分析。約束部分最重要的參數是陰影價格，通常也稱影子價格。影子價格是指線性規劃模型中某個約束的右端常數項增加（或減少）一個單位而導致的目標函數值的增量（或減量）[10]。影子價格客觀地反映了資源在系統內的稀缺程度，影子價格越高，這種資源越稀缺。而影子價格為零的約束資源為富余資源。由陰影價格的定義可得出，陰影價格反映的是單位資源（消耗）的價值（費用）。

第一個約束銷地Y1的影子價格是11，說明銷地Y1每增加1個需求量，目標函數運輸總費用會增加11個單位。也就是說，目標函數的最優解會發生變化，從“允許的增量”一欄中可以看出，實例中銷地Y2的陰影價格最大，說明Y2每增加1個需求量所增加的運輸總費用最高。但從表3可以看出，銷地Y1、Y2、Y3和Y4“允許的增量”為0，產地X1、X2和X3“允許的減量”也為0，說明銷地增加需求量和產地減少生產量都將導致最優解發生改變。

現在假設如果市場條件已發生變化，生產量和需求量需要同時增加（或減少），仍然保持產銷平衡狀態。當生產和需求同時增加時，X1和X2允許的增量都為5（萬件），X3允許的增量為任意值，假設總的需求量增加5（萬件），生產量也要同時增加5（萬件），這時仍滿足產量和銷量相等。運用Excel進行進一步求解分析，目標是當生產量和需求量各增加5（萬件），保持產銷平衡，得出運輸總費用增加最少的最優化方案，所得結果數據如表6所示。

表6 運輸總費用增量表

從表6可以看出，在X2生產量增加5（萬件）和Y1需求量增加5（萬件）的情況下運輸總費用增加最少，這是因為在表3中，產地X1的陰影價格為-6，X2對應的陰影價格為-10，X3的陰影價格為0，說明X2增加產量比X1和X3對總費用的降低最大。同時，銷地Y1對應的陰影價格為11，Y2對應的陰影價格為19，Y3對應的陰影價格為15，Y4對應的陰影價格為13，說明Y1增加需求量比Y2、Y3和Y4對總費用的增加最小。因此，在生產量和需求量都同樣增加保持產銷平衡的情況下，在產地X2處生產最劃算。同理，在生產量和需求量都同樣減少保持產銷平衡的情況下，不難判斷在X3處減少生產最合理。

4 結束語

Excel在數據處理和分析方面還有很多重要應用，比如通過統計分析對大量數據進行統計處理；通過回歸分析找到數據內在規律，并可用于預測和控制等問題；通過時間序列分析進行市場預測以及制定生產計劃等。但最重要的是要理解數據背后所表達的現實含義。文章以線性規劃中的運輸問題為例，通過對數據處理結果進行分析，揭示敏感性報告中的重要參數的現實內涵，通過驗證證明了結論的正確性，對于使用Excel進行數據處理和分析的人員具有一定的參考價值。