一種新型的改進果蠅優化算法

戈濤，張馨

（1.合肥市現代職業教育公共實訓中心，合肥230012；2.安徽大學計算機科學與技術學院，合肥230601）

0 引言

果蠅優化算法是臺灣學者潘文超在2011 年提出的新型群體智能優化算法[1-2]，主要是模擬果蠅搜尋食物的過程，果蠅有著優于其他物種的敏感嗅覺器官，能夠嗅到漂浮在幾十公里外空氣中的各種食物味道，當靠近食物位置時又能通過其敏銳的視覺找到食物和同伴，并向味道濃度最大的方向飛去。果蠅算法就是通過模擬此過程并不斷迭代尋優以求得問題的最優解。果蠅優化算法自誕生之日起就以其算法簡單、調整參數少、易實現等優點而受到廣大學者的青睞，現已被廣泛應用與求解函數優化[3]、PID 控制參數優化[4]、最小二乘支持向量機參數優化[5]、置換流水線調度[6]、LSSVR 干燥速率建模[7]、多維背包問題[8]等。隨著對果蠅優化算法的不斷深入研究，算法本身也暴露出了不可忽視的缺點。果蠅優化算法在求解單峰值函數時尚能表現出良好的尋優效果，但是在求解多峰值或者高維度的復雜優化問題時很難達到理想的效果。

為了解決原始果蠅優化算法自身存在的收斂速度慢、尋優精度低、易陷入局部最優等問題，本文提出了一種新型的果蠅優化算法，將本文方法與原始果蠅優化算法及改進的果蠅算法DS-FOA 和LGMS-FOA 進行仿真對比，實驗結果表明，本文所提出的算法在收斂效果和尋優速度上有了明顯提高且具有更高的穩定性。

1 基本果蠅優化算法介紹

1.1 FOA算法描述

在基本果蠅優化算法中，每只果蠅個體會被隨機的分布在一個N 維的特定搜索空間，其搜索步長固定不變，搜尋食物的方向具有隨機性，每個果蠅個體都攜帶有味道濃度，該值與味道濃度判定值有關，由于在初始階段不知道食物的具體位置，因此把每個果蠅個體與原點距離的倒數作為判斷味道濃度判定值的依據，將該值代入目標函數以求得果蠅個體的味道濃度值，味道濃度值越小的果蠅距離食物源的位置越近（適用于最小優化問題），記錄下果蠅群體中味道濃度值最小的果蠅位置，其他果蠅憑借敏銳的嗅覺飛往該位置，最后通過迭代不斷更新果蠅群體中的最佳位置，直到迭代結束找到問題的最優解。

1.2 FOA具體步驟

FOA 算法主要分為7 個步驟：果蠅群體位置初始化，果蠅飛行方向和距離，味道濃度判定值計算，味道濃度值計算，計算最佳味道濃度，保留最佳味道濃度值及其位置，迭代尋優。

（1）果蠅群體位置初始化

設定果蠅群體規模和最大迭代次數分別為Sizepop、Maxgen,果蠅群體位置為X_axis,Y_axis。

（2）果蠅飛行方向和距離

其中，RValue 為果蠅的隨機搜索距離。（3）味道濃度判定值計算

計算果蠅個體與原點的距離（Di）和果蠅個體的味道濃度判定值（Si）：

（4）味道濃度值計算

將味道濃度判定值Si代入適應度函數Function中，求出該果蠅個體位置的味道濃度smell(i)：

smell(i)=Function(Si)

（5）計算最佳味道濃度

找出此果蠅群體中的最優個體（即味道濃度最小值）以及其位置：

[bestsmellbestindex] =min(smell)

（6）保留最佳味道濃度值及其位置

保留最優味道濃度值bestsmell 與其對應的X、Y 坐標，此時果蠅群體往該位置飛去：

（7）迭代尋優

重復執行步驟（2）-（5），并判斷味道濃度是否優于前一迭代味道濃度，若成立則執行步驟（6）。

1.3 基本FOA的缺陷

缺陷一：基本FOA 算法中，果蠅個體在搜索空間內移動步長是固定不變的，選擇一個固定的移動步長值求解優化問題是不恰當的，尤其是對于多峰值函數，若搜索步長值取得較大，在算法前期尚可獲得較快的尋優速度，進行全局搜索，但是到了算法尋優后期較大的移動步長極有可能跳過函數最優解，尋優精度降低，陷入局部最優；若搜索步長值取得較小值，雖然尋優精度提高了，但是步長值較小會降低了尋優速度，需要不斷重復的迭代，降低了尋優效率，不利于進行全局尋優。

缺陷二：基本FOA 算法中，在果蠅視覺搜索過程中，果蠅群體一旦發現具有最優味道濃度的果蠅，所有果蠅個體都會飛往該果蠅的位置，可是該果蠅極有可能并不是整個搜索空間中的最優果蠅個體，而是局部最優果蠅個體，若此局部最優果蠅個體周圍沒有比其味道濃度更優的果蠅，它就會保持不動，其他果蠅則源源不斷地飛往此果蠅的位置，不但降低了尋優效率，也容易使算法陷入局部最優。

2 改進的FOA算法（CSFOA）

2.1 非線性遞減步長

針對基本FOA 算法中的缺陷一，CSFOA 算法中變固定步長值為非線性遞減步長，移動步長變化率如圖1所示，在果蠅算法迭代尋優初始階段，果蠅個體保持一個較大的移動步長，使算法的搜索能力能夠滲透到整個搜索空間，從而提高算法全局尋優的能力，避免算法陷入某個局部最優值；在果蠅算法迭代尋優后期，果蠅個體的移動步長非線性的動態逐漸減小，使其能在當前局部最優解附近進行精細搜索，不僅避免了因為移動步長值過大而跳過最優解可能，而且也提高了算法后期的收斂精度。

圖1 移動步長變化率

具體公式如下：

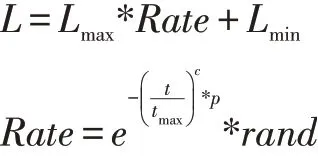
其中Lmax，Lmin分別為最大和最小移動步長，Rate為步長的變化率，t 為當前迭代次數，tmax為最大迭代次數，p 為步長調節因子，c 為指數調節因子。

2.2 隨機策略

針對基本FOA 算法中的缺陷二，本文引入了隨機機制，增加算法探索解空間的能力，若某個最優解經過多次迭代始終不變，則此時極有可能陷入局部最優解，如圖2 所示，因此引入隨機策略進行擾動，使算法逃離局部最優，增加解得多樣性，從而進行全局搜索。具體策略如下：

其中（1-e-λx）滿足指數分布，besti-1為上一代最優味道濃度值。

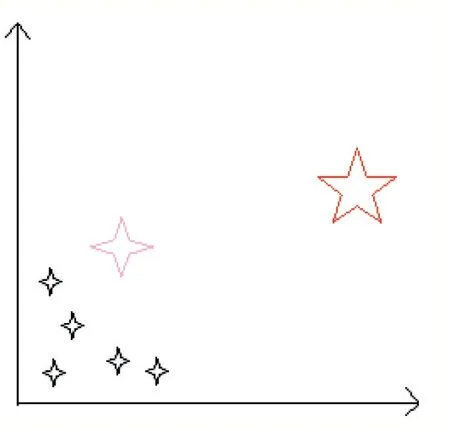
圖2 局部最優實例

3 仿真實驗及結果分析

3.1 實驗平臺

本文的實驗平臺是MATLAB R2014a,在操作系統為Windows 7，內存為4GB，CPU 頻率為3.20GHz 的PC上運行。

3.2 參數設置

具體參數設置如下：果蠅群體大小Sizepop=20，迭代次數tmax=100，步長調節因子p=1，指數調節因子c=1.5，最大移動步長Lmax=5，最小移動步長Lmin=0.01，隨機策略中的λ=0.5。

3.3 測試函數

為了驗證算法的可行性，本文選取8 個基準測試函數對FOA、DS-FOA、LGMS-FOA 以及本文算法進行測試，求出在指定搜索區間內的函數最優值，測試函數如表1 所示。

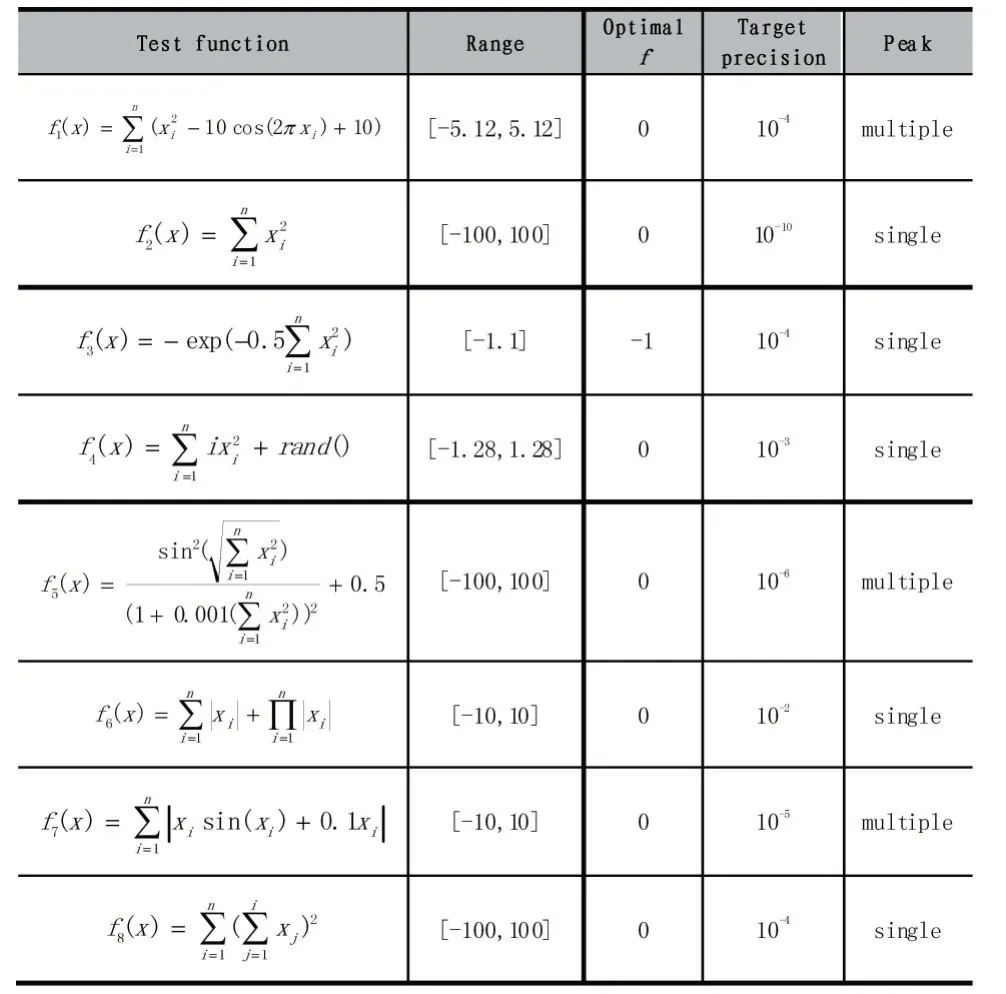
表1 測試函數

3.4 仿真實驗

使用基本FOA、DS-FOA、LGMS-FOA 以及本文算法CSFOA 對8 個基準函數獨立運行實驗20 次，分別求出8 個基準測試函數的平均值以及標準偏差，函數的平均值反映了算法的尋優能力，標準偏差則能夠反映出算法的穩定性。在MATLAB 上經過20 次獨立運行的實驗結果如表2 所示，其中Mean、Std 分別代指函數的平均值和標準偏差。

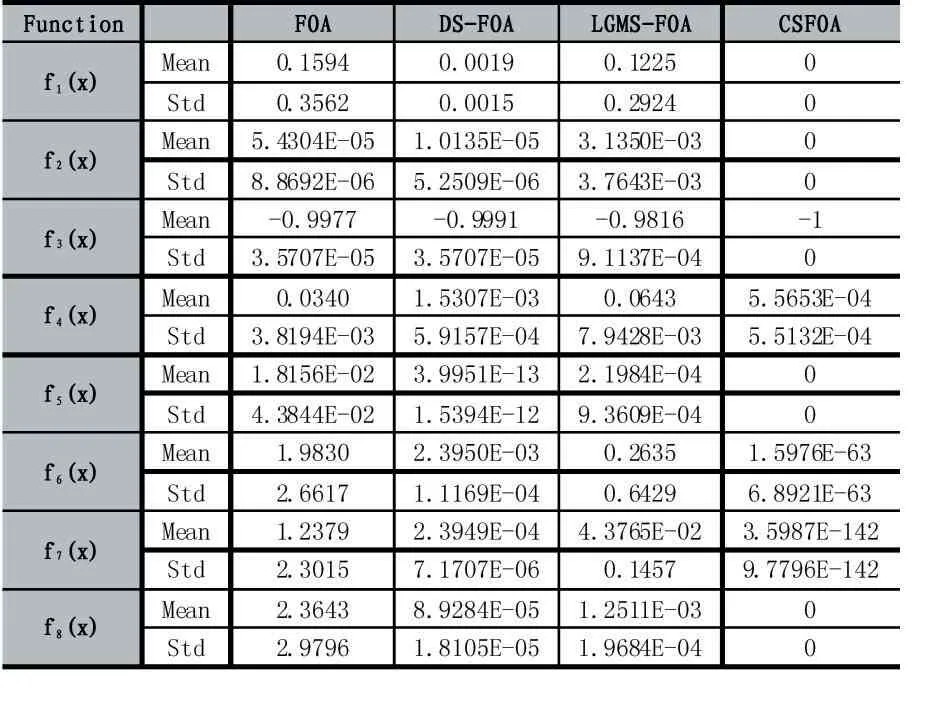
表2 四種算法優化性能對比

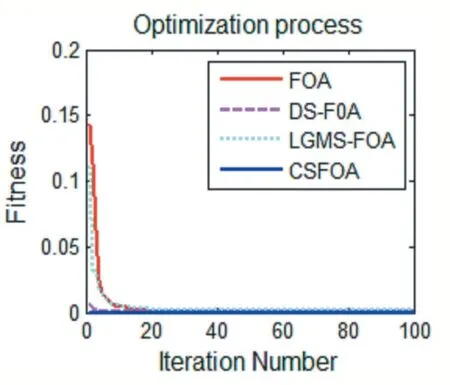
圖3 f1(x)函數優化對比

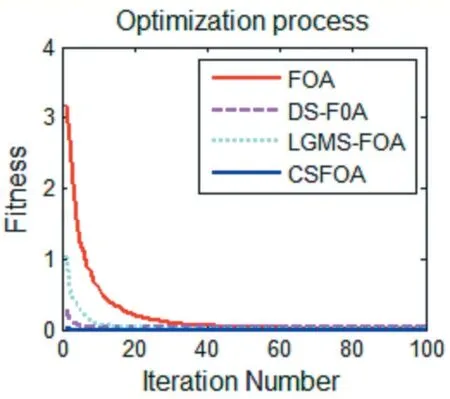
圖4 f2(x)函數優化對比

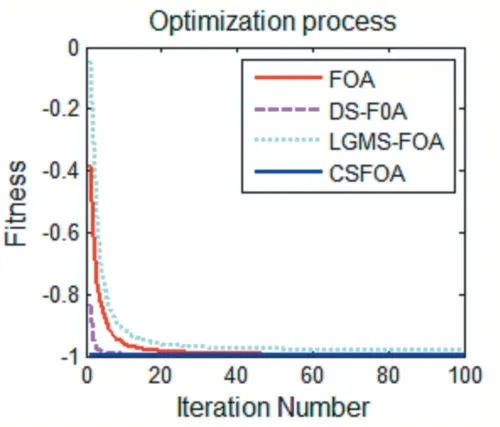
圖5 f3(x)函數優化對比

圖6 f4(x)函數優化對比

圖7 f5(x)函數優化對比

圖8 f6(x)函數優化對比

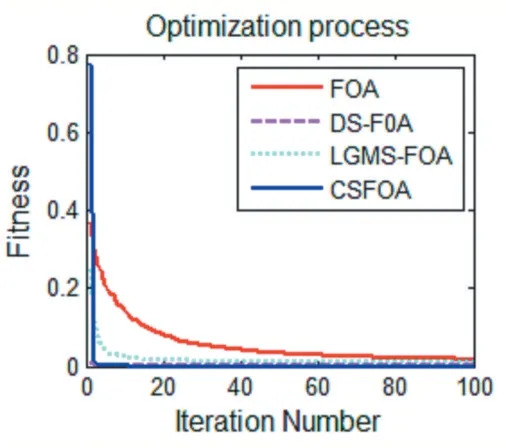
圖9 f7(x)函數優化對比

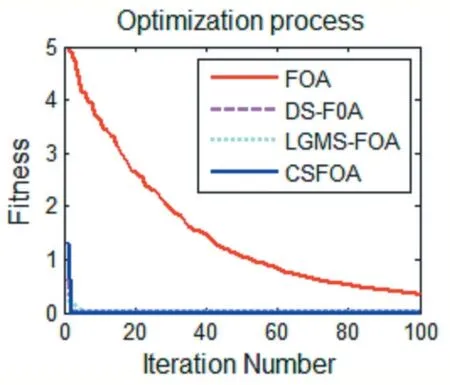
圖10 f8(x)函數優化對比

從表2 中可以看出，在求解高維函數的最優值時，原始FOA 算法的弊端尤其明顯，由于原始FOA 采用固定的步長值，限制了算法的尋優性能，導致算法容易陷入局部最優；相較于原始FOA，DS-FOA 引入了初始步長L0，使算法能夠隨著迭代的進行移動步長逐漸減小，提高了算法在迭代后期的收斂精度；LGMS-FOA 則是引入了權重系數w，并且隨著不斷迭代權重系數w 按指數形式下降，相較于原始FOA 同樣提高了算法的收斂精度，但是在對函數f2(x)、f3(x)、f4(x)求解中其收斂精度卻低于原始FOA 的收斂精度，原因在于LGMSFOA 算法并沒有解決算法陷入局部極值的問題。與其他三種算法相比，CSFOA 算法不管是在收斂精度還是算法穩定性方面都有著明顯的優勢。

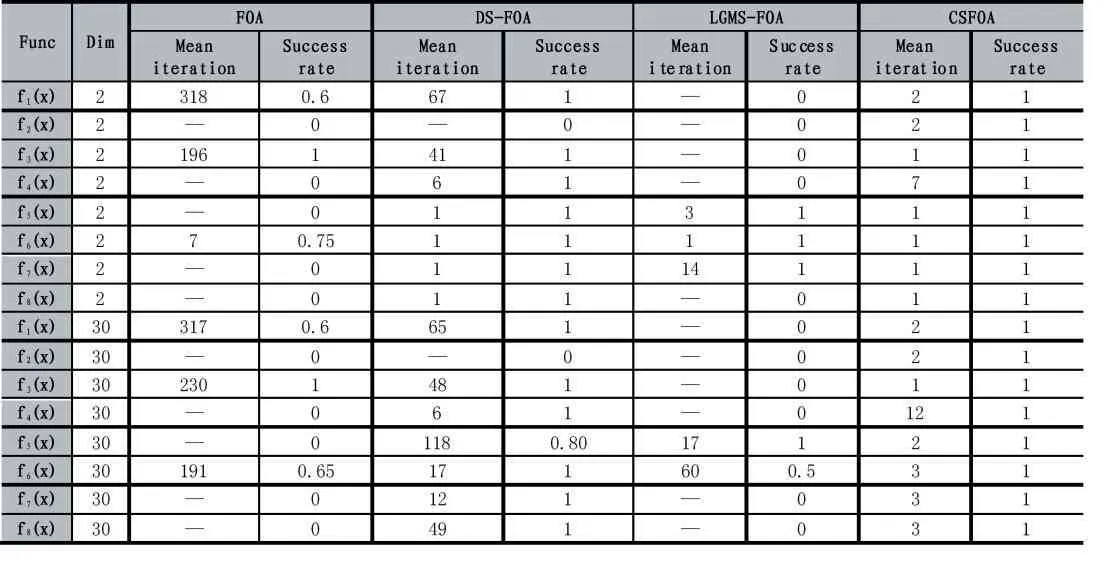
表3 目標精度下平均迭代次數與成功率對比

圖3～圖6 為四種算法的迭代尋優過程，從中可以看出，原始FOA 算法收斂速度較慢，DS-FOA 和LGMS-FOA 算法收斂速度雖有提高，但是容易陷入局部最優，而CSFOA 算法由于采用了隨機策略，即使遇到局部最優解也能及時跳出局部極值，尋找到函數最優解，提高了算法的尋優性能。

表3 為8 個基準測試函數在目標精度下所需要的迭代次數和成功率的結果對比，從中可以看出，在低維情況下，三種改進的FOA 算法有著更強的尋有能力，迭次數更少，且成功率高；在高維情況下，原始FOA 算法、DS-FOA 算法和LGMS-FOA 算法的尋優能力下降，易陷入局部最優，且在完成目標精度情況下需要經過多次迭代，影響了算法的尋優效率，而CSFOA 算法在低維和高維情況下都表現出了良好的尋優能力，且具有更高的效率和穩定性。

4 結語

本文針對基本果蠅算法的缺陷，提出了非線性動態機制，將基本果蠅算法中的固定步長變為非線性遞減步長，既保持了算法在迭代初期全局尋優的能力，又維持了算法在迭代后期進行精細搜索的能力；為了增加算法在整個尋優空間中探索解空間的能力，引入了隨機策略，對空間解進行擾動，避免算法陷入局部最優。仿真實驗結果表明，改進后的算法具有更好的探索解空間的能力，有效避免了算法陷入局部極值，增加了算法的穩定性，提高了運行效率。接下來的研究任務是將新改進的算法用于解決實際問題，驗證其解決問題的能力和效率。