基于水下高速小目標末彈道測量的實孔徑成像聲吶波束形成研究

張思宇，何心怡，陳 菁，王 磊

(1.海軍研究院，北京 100161；2.中國科學院聲學研究所，北京 100097)

0 引 言

在聲吶系統的設計過程中，波束形成是一個核心基礎環節，利用一定幾何形狀的基陣和信號處理技術，使發射和接收的信號形成指向性波束。在發射信號時，通過指向性波束提高聲吶的作用距離；在接收信號時，在空間域中抑制環境噪聲和混響干擾，提高聲吶接收機輸入端的信噪比，獲得更好的聲吶圖像和目標的分辨率，其直接表征為旁瓣級，旁瓣級越低，系統抑制旁瓣區域的干擾能力越強。

在沒有水下彈道測量系統的條件下，設計測量水下高速小目標末彈道的聲吶成像系統的主要考慮：1）目標接近成像系統的方向未知，可能從任一方向接近；2）目標運動速度快，回波多普勒偏移量大，可能達到寬帶信號的標準；3）目標距離近，成像系統受到混響的干擾強等因素的限制[1]。在聲吶系統的陣型設計中，只有使用均勻排布的圓形陣列，才具有 0°～360°的方位角范圍內，形成均勻指向性波束的能力，避免目標的方位模糊，圓陣波束形成數學模型簡單，設計的工程實現性強。但是圓陣的常規波束形成的旁瓣級高，圖像的目標分辨率低，彈道測量誤差大，本文以一種對均勻圓陣進行Dolph-Chebyshev 加權的波束形成方法，并給出在圓陣利用此法波束形成的約束條件，并通過仿真實驗驗證方法的可行性。

1 常規波束形成模型

由于聲信號到達基陣各個陣元的距離不同，導致各個陣元輸出的信號也不同，需要通過延時等信號處理方法補償差異，這是常規波束形成的基本思想[2-3]。假設入射信號是平面波，基陣是N 個陣元組成。以其中某個陣元為參考點， 設第 i個陣元接收的信號為s[t +τi(θ0)]， 其中 θ0為預設的信號入射角，對各通道信號延時補償 τi(θ0) ， 使各路輸出信號均為 s(t)， 再對N 路信號求和、平方和積分就得到，其中為信號功率。此時，信號如從 θ角入射，則第 i個陣元輸出信號為 s[t +τi(θ)?τi(θ0)]，陣列輸出為：

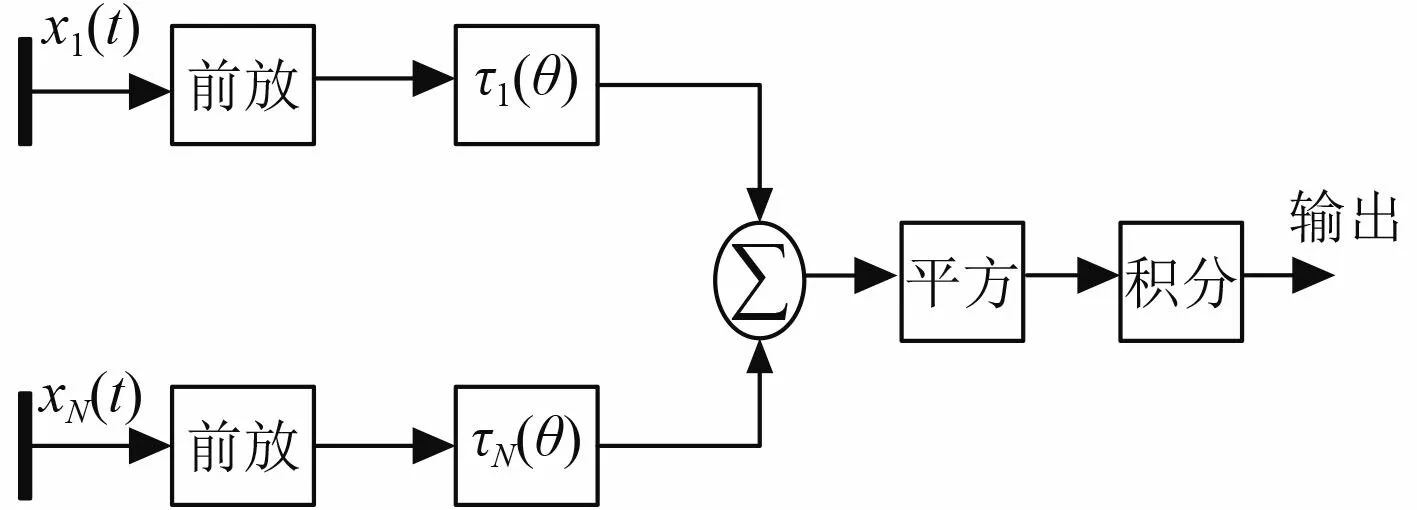
圖 1 常規波束形成模型Fig.1 Conventional beamforming model

2 圓陣波束形成的信號模型

目前，陣元發射信號受到換能器諧振頻點的限制，一般只能發射窄帶信號。接收信號則根據信號的不同分為窄帶信號模型和寬帶信號模型，通常當目標回波信號帶寬大于信號中心頻率的1/10 時，被認為是寬帶信號，由于發射信號和接收信號的波束形成原理相同[3]，文中以接收的信號模型為例說明。

被測目標到成像系統的距離一般是遠大于成像系統的圓陣直徑，陣元接收的信號屬于遠場窄帶信號。假設回波信號為 s(t) ， 圓陣的陣元數為 N，圓陣接收的信號可以表示為：

式中， f0為 信號的中心頻率， a (t) 為信號幅度， φ (t)為信號相位，其解析信號可以表示為：

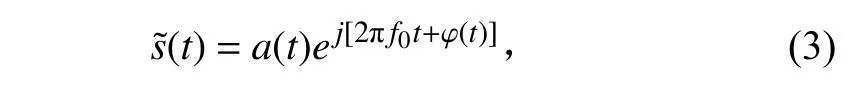
假設接收信號的時延量為τ,圓陣接收信號為：

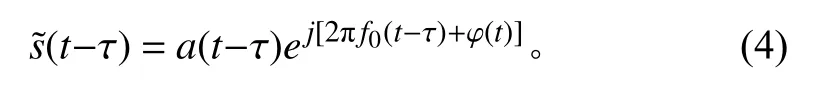
但是，窄帶信號的幅度是慢變化的，則a (t?τ)=a(t)。可見，窄帶信號時延只會引起信號復包絡的相移變化，對信號的幅值的影響基本可以忽略。假設圓陣的參考陣元的接收信號為第i個陣元接收信號相對參考陣元接收信號的時延量為 τi，其信號可表示為：

圓陣在第n 次快拍接收到的信號模型可用矩陣表示為：

3 圓陣波束形成的數理模型

3.1 均勻加權波束形成

假設圓陣半徑為 R， 在其圓周上等間距排布 N 個陣元，以原點作為參考點，依次確定信號到達各陣元的時延量，如圖2 所示。

圖 2 均勻圓陣陣元分布圖Fig.2 Distribution of uniform circular array elements

其中， ?R 為參考原點和第i 個陣元的波程差。則第i 個陣元和參考原點之間的相位差為：

整個均勻圓陣的波束響應可以表示為：

式中， si(θ,φ)為 第 i 個 陣元的接收信號， ωi為 第 i 個陣元接收信號的加權值。

在均勻圓陣上，采用均勻加權法進行波束形成，則有：

整個均勻圓陣的波束響應可以表示為：

3.2 旁瓣抑制加權波束形成

通過Dolph-Chebyshev 加權法抑制旁瓣高度，改善圓陣波束形成的性能，但是以上加權法只適用于線性陣列，故需要通過相位模式激勵法將圓陣等效成線列陣，再進行后續的波束形成[4-5]。為了方便討論波束性能，令則方位角為 φ，此時參考陣元 i的接收信號響應為：

定義矩陣 J 和 F分別為：

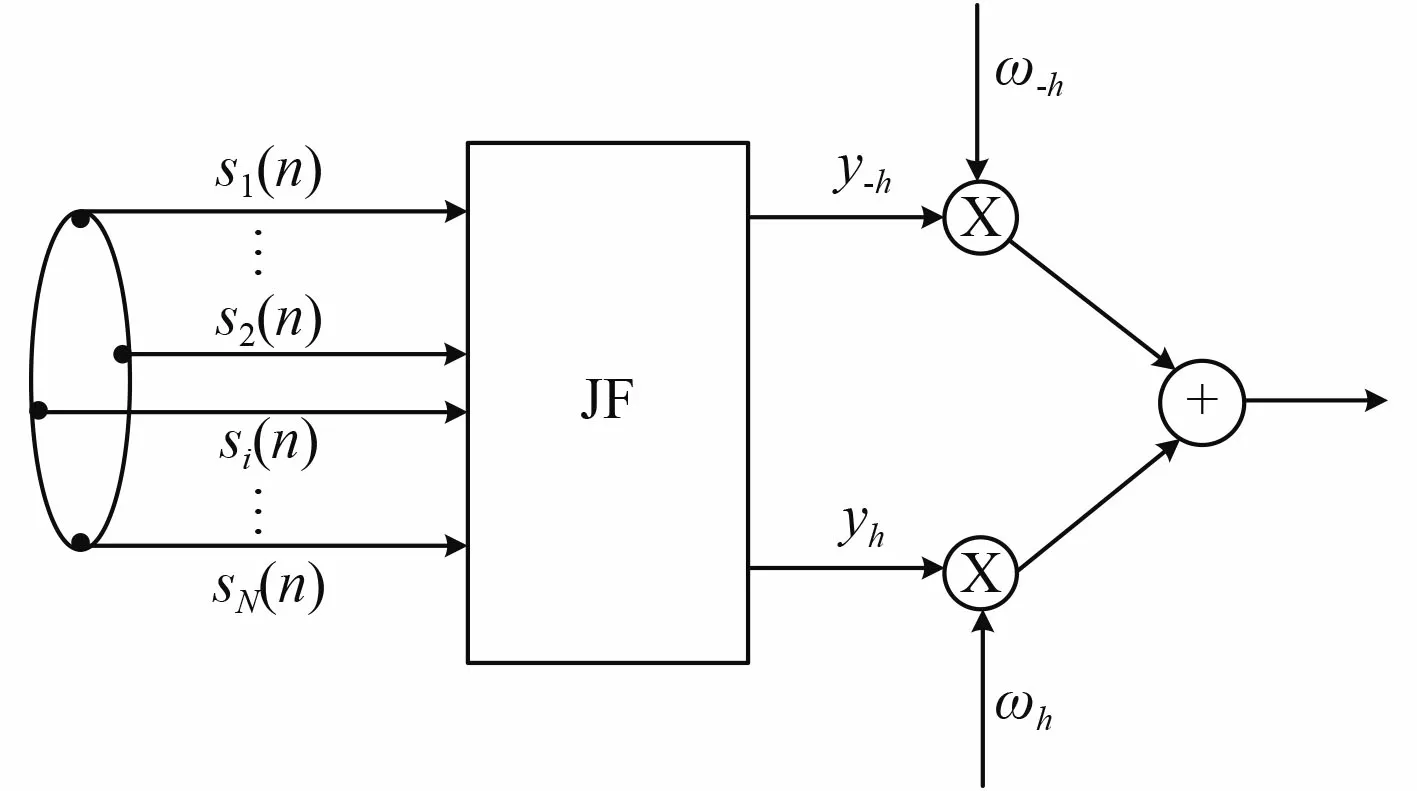
圖 3 圓陣響應模式轉換模型圖Fig.3 Model diagram of response mode transformation of circular array

經過轉化后，陣元信號響應矩陣為：

形成了線列陣的響應模式，具有范德蒙行列式的結構形式，在此基礎上，可以按照Dolph-Chebyshev 加權法對輸出信號 yi(n),i = ?h,···,h進行波束形成，假設波束指向 φ1方 向，設置權向量 W：

則整個整理的波束響應為：

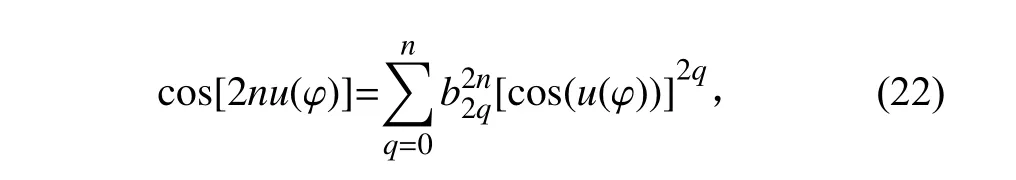
B(φ)

即，波束響應 可以轉化為：

令 β為主瓣幅值和旁瓣幅值的比值，將式（22）表示成根值 z ∈[?1,1]且 還有 2h項的Chebyshev 多項式：

式 中， z = z0cos(u(φ)),z ∈[?z0,z0] 。 其 中， z0有T2h(z0)= β ＞1決定，可以進一步得到：

圓陣響應模式可表示為：

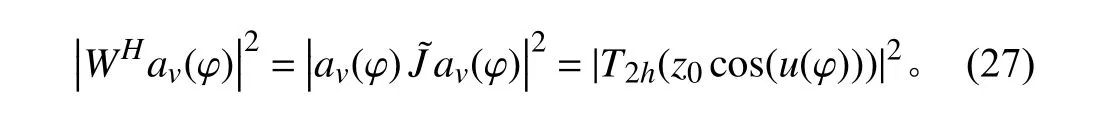
此時，圓陣波束響應模式已經等效為均勻線列陣Dolph-Chebyshev 多項式的響應模式。因為 u(φ) 和 φ1成線性關系，對于任一取值的 φ1， 圓陣波束響應 B(φ)主瓣寬度都相同，即任一波束指向方向的圓陣波束響應的主瓣寬度一致。對于任一方向接近的目標，其波束響應的強度相同，有利于均衡圖像的背景，提高目標的圖像分辨率。

值得注意的是上述陣列模式等效轉換需要滿足矩陣 BJF可逆的條件，即圓陣的陣元數圓陣的陣元間距必須小于回波信號的半波長。下面通過仿真實驗經過Dolph-Chebyshev 加權后的旁瓣抑制效果。

4 圓陣波束形成仿真實驗及性能分析

仿真實驗1：假設均勻圓陣共有33 個各向同性的陣元，圓陣半徑為 R， 接收信號的波長為 λ。要求波束指向 (0°,0°)方向，經過Matlab 仿真得到圓陣的波束指向性圖，如圖4 所示。

由圖4 可知，圓陣三維波束形成圖可以獲得均勻加權圓陣的俯仰角和方位角信息，反映了均勻加權波束形成性能。但是，實孔徑聲吶成像系統和被測目標基本在同一深度，故方位角信息更值得關注。為了方便分析圓陣波束形成水平方向的指向性特征及討論不同陣元數和半徑的波束指向性能。

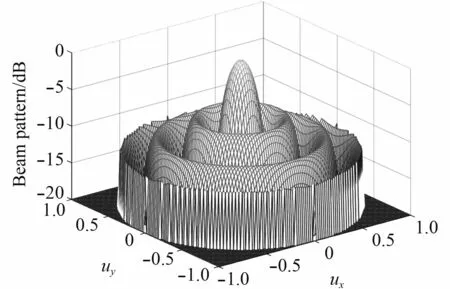
圖 4 均勻加權圓陣三維波束形成圖Fig.4 Uniform weighted circular array three-dimensional beamforming

圖 5 均勻加權圓陣二維波束形成圖Fig.5 Two-dimensional beamforming of uniformly weighted circular array

由圖5 可知，均勻加權圓陣水平方向的半功率波束寬度1 1.5°， 最大旁瓣高度約為 ? 8 dB，遠離預成方向的旁瓣呈現遞減趨勢。

仿真實驗3：其他實驗假設條件不變，保持 R/λ=0.66 不變，改變陣元數 N，得到圖6。

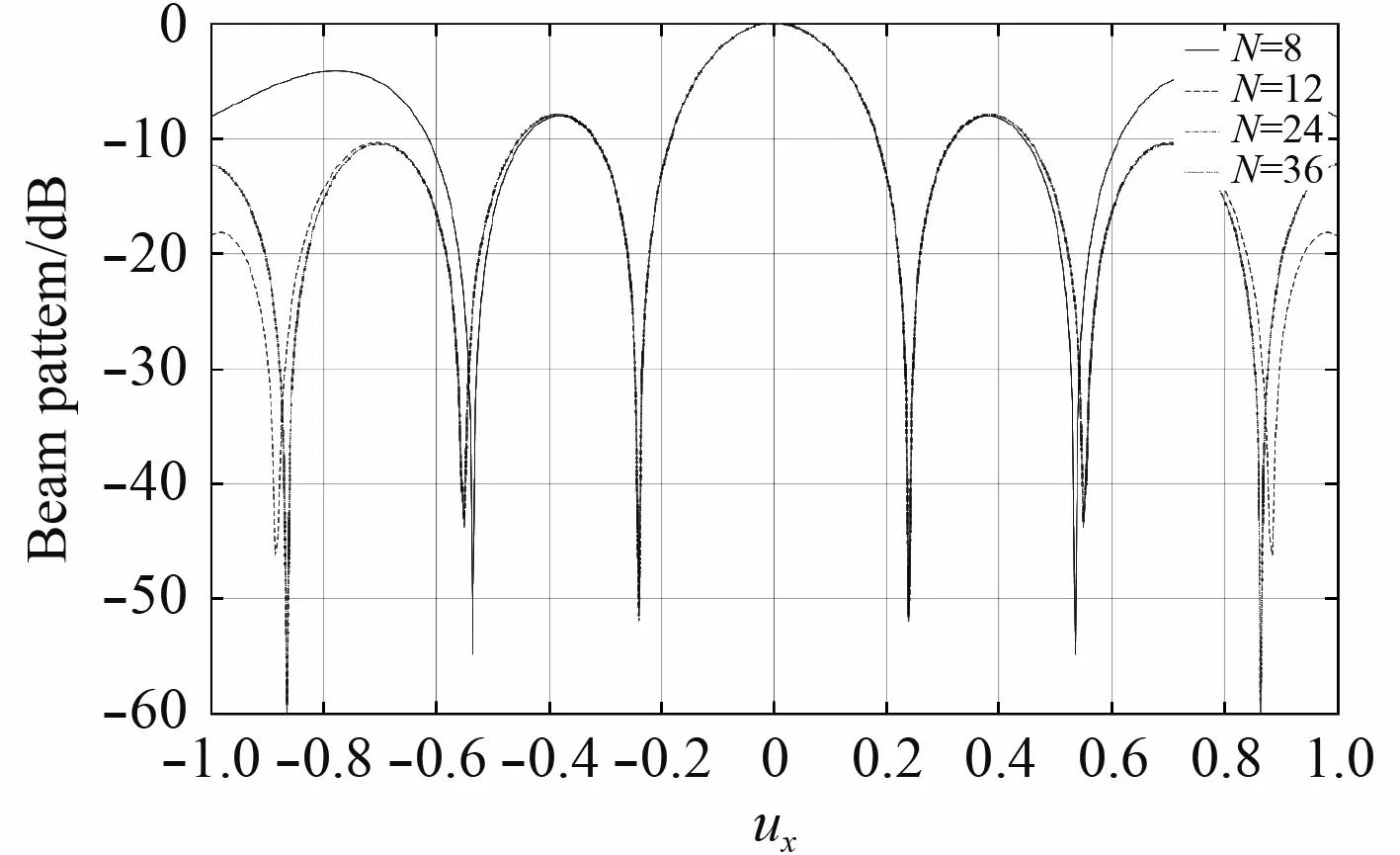
圖 6 信號頻率一定不同陣元數圓陣二維波束形成圖Fig.6 Two-dimensional beamforming of circular arrays with different signal frequencies

由圖6 可知，由于圓陣的非線性特點，在調整圓陣半徑和接收信號波長比值不變的情況下，無論怎樣改變圓陣陣元的數量，均勻加權圓陣的第一旁瓣高度總是約為-8 dB，明顯高于線列陣的第一旁瓣-13.5 dB的高度。高旁瓣會引起高的虛警概率，造成大的彈道測量誤差，應當在設計中采用適當的方法抑制旁瓣，保證測量精度。

仿真實驗4：實驗1 的其他假設條件不變，改變圓陣接收信號頻率，即改變圓陣的半徑和信號波長比，得到圖7。

圖 7 圓陣半徑一定不同頻率信號二維波束形成圖Fig.7 Two-dimensional beamforming of signals with certain circular array radius and different frequencies

由圖7 所示，在圓陣陣形固定的條件下，提高發射信號頻率可以減小波束形成的主瓣寬度，改善波束指向性能，但是最大旁瓣高度仍為-8 dB 左右，虛警概率和軌跡測量依然較大，且提高發射信號頻率會導致信號吸收損失的增強，限制了聲吶系統的作用距離，需要慎重選擇發射頻率。

仿真實驗5：設圓陣具有32 個均勻排布的陣元且陣元各向同性，半徑波長比為0.75，主瓣幅值和旁瓣幅值比為 β =10（ ? 20 dB ），令波束指向 ( 0°,0°)方向，俯仰角，最大相位模式 h = 5，則圓陣chebyshev 加權部分可以等效為11 個陣元均勻排布的線列陣，利用Matlab 仿真，分別得到均勻加權圓陣波束響應圖和Dolph-Chebyshev 加權圓陣波束響應圖，如圖8 和圖9 所示。

5 結 語

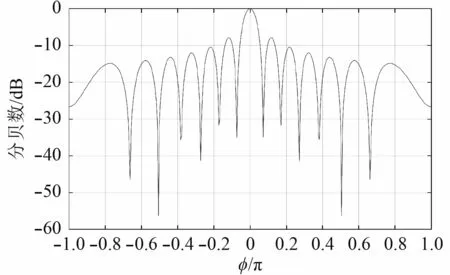
圖 8 均勻加權圓陣二維波束形成圖Fig.8 Two-dimensional beamforming diagram of uniform weighted circular array

圖 9 Dolph-Chebyshev 加權圓陣二維波束形成圖Fig.9 Dolph-Chebyshev weighted circular array 2-D beamforming

設計基于水下高速小目標末彈道測量的實孔徑成像聲吶應該優先考慮均勻排布的圓陣，保證沒有觀測盲區，提高觀測效率。在圓陣做波束形成時，Dolph-Chebyshev 加權法能夠有效抑制旁瓣高度，克服均勻加權圓陣波束形成旁瓣高的缺陷，同時能夠保證在各個波束方向上，波束響應的幅值相同，為后續圖像信號處理提供高質量的輸入信號。但是，圓陣陣元數必須滿足才能等效成線列陣的響應模式進行Dolph-Chebyshev 加權，否則常規波束形成的方法旁瓣抑制效果均不理想，故為了獲得良好的目標回波圖像采用Dolph-Chebyshev 加權時，必須合理設計圓陣半徑、發射信號頻率和陣元數量的關系以滿足 BJF矩陣可逆。