陣元數對組合線陣近場目標定位性能的影響*

李昆鵬 康春玉 夏志軍 張聞龍 張 億

（1.海軍大連艦艇學院學員五大隊 大連 116018）（2.海軍大連艦艇學院水武與防化系 大連 116018）

1 引言

隨著降噪技術的不斷發展，水下目標輻射噪聲級不斷降低，隱蔽性隨之增強。近場區域警戒和近海岸的港口防御等軍事需求越來越迫切［1～2］。針對近場聲目標定位問題，聚焦波束形成是常見的方法之一，其原理就是根據目標聲源到各個陣元曲率半徑不同，補償球面波傳播模型下的時延差，并對補償后的陣元信號進行加權求和，聚焦波束形成輸出會出現峰值，其峰值所應的角度即為目標信號的方位。科研人員基于均勻線列陣，對近場聚焦波束形成方法展開了比較深入的研究，2010年，熊鑫等［3］系統地研究了基于線列陣的最小方差無失真響應（Minimum Variance Distortionless Response，MVDR）聚焦波束形成方法，仿真結果表明，MVDR聚焦波束形成方法能夠有效解決因線陣陣元間距增大而導致的“混疊”問題，提高了聚焦空間分辨率。2014年，劉凱等［4］提出了一種基于矩陣空域預濾波處理的近場聚焦波束形成方法，該方法有效提高了對弱輻射噪聲目標的定位能力，進一步優化了聚焦波束形成方法，從目前的研究情況來看，基于單線陣的近場目標的定位研究主要集中于方位估計或方位與俯仰角估計，且仍然無法解決“左右舷模糊”等問題。針對基于空間陣的目標距離、方位、俯仰角三維同時定位需要進行更深入的研究。研究也表明，定位性能與基陣的布設、定位的方法等都有比較大的關系，如何設計更合理的小尺寸基陣實現對近場目標的準確定位仍然是需要解決的問題［5～6］。

本文提出組合線陣設計的構想，推導了組合線陣的接收信號模型，提出了近場三維聲聚焦波束形成的實現框架，通過對切割球面上聚焦點的掃描，得到目標方位角和俯仰角，再通過對不同掃描球面上最大輸出功率的比較得到目標距離，從而實現了對近場目標距離、方位角、俯仰角的估計，并采用常規波束形成方法仿真分析了組合線陣陣元數對目標三維定位性能的影響，可為組合線陣的陣形設計提供一定支撐。

2 組合線陣近場信號接收模型

如圖1所示，組合線陣由4條線型子陣組成，每條子線陣的陣元數為m，則整個基陣的總陣元數M=4m。4條線型子陣與水平面的傾斜角度均為θz，單條子陣的長度為d且陣元間距相等，以四條線陣的對稱中心為圓心建立坐標系，每條線陣距離圓心均為l1，假設近場聲源S的位置為( )r，θ，φ ，其中r表示聲源到參考點的距離，θ表示俯仰角，φ表示方位角。聲源 S 到第 k（k=1，2，...，4）條子陣第 i個（i=1，2，...，m）陣元的距離為 rki。

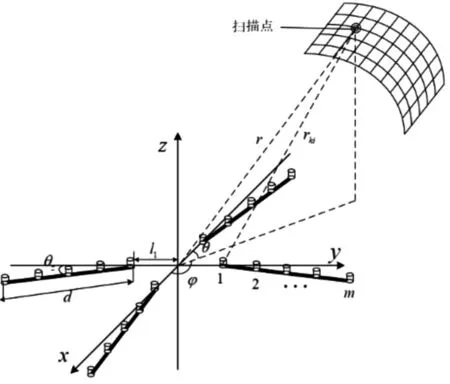
圖1 組合線陣陣列模型

根據和幾何關系，運用三角形余弦定理可得

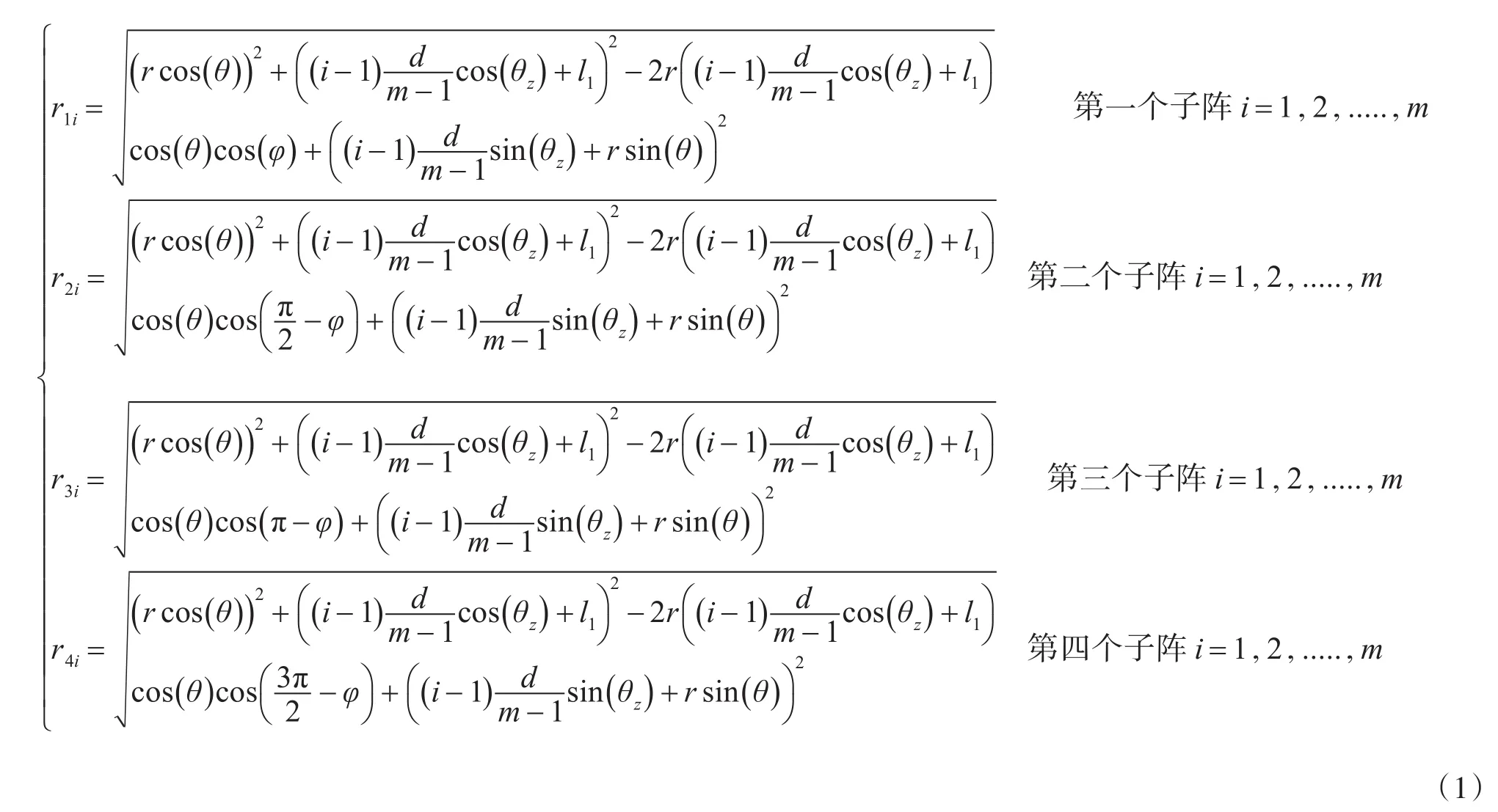
第 k（k=1，2，...，4）條子陣第 i個陣元收到信號與參考點的時延差為

則第 k（k=1，2，...，4）條子陣第 i個陣元的接收信號可表示為

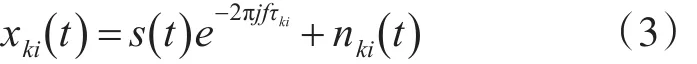
表示為矩陣形式為

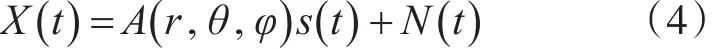
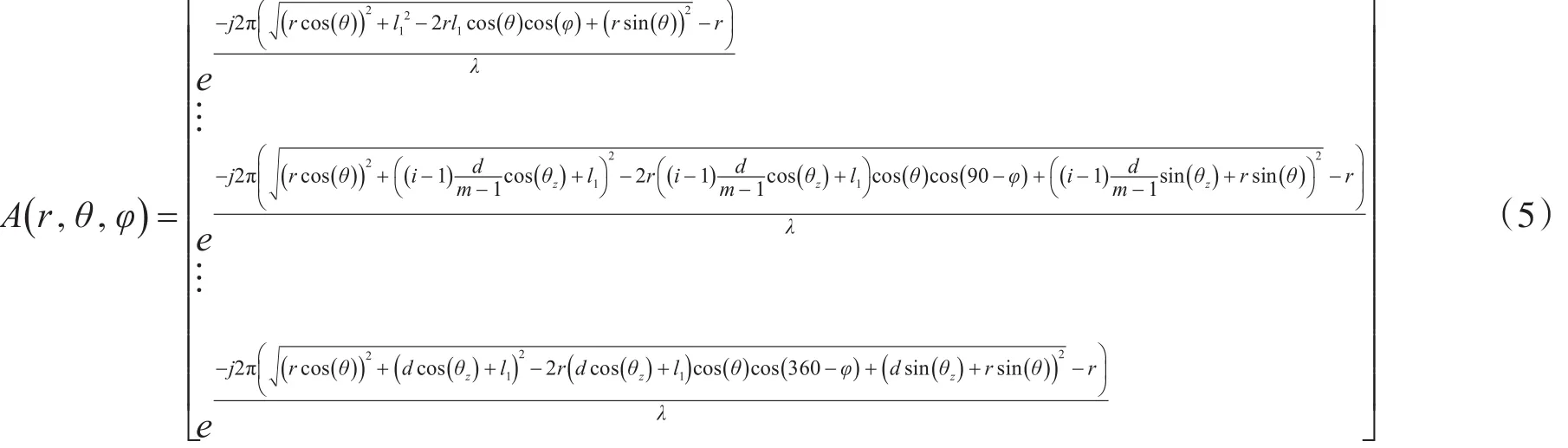
3 三維聲聚焦波束形成原理

常規聚焦波束形成，就是根據目標聲源到各個陣元曲率半徑不同，補償球面波傳播模型下的時延差，并對補償后的陣元信號進行加權求和，聚焦波束形成輸出會出現峰值，其峰值所應的角度即為目標信號的方位，其傳統方法的時延差是聲源距離和方位的二維函數，在掃描平面上對不同位置點進行掃描，獲得該平面的聲強圖，當掃描點與目標位置重合時，聚焦波束形成輸出會出現峰值，即可得到目標的距離和方位估計［7～10］。

本文在常規聚焦波束形成的基礎上，提出三維聲聚焦波束形成方法。

首先，以坐標系原點為中心，將搜索目標的距離范圍切割為Q個掃描球面，每個掃描球面的半徑差為10m，對每一個掃描球面rq再以1°為間隔，將掃描球面 rq劃分為181×361個掃描點［11～12］。

對rq（掃描球面距參考點的距離）球面上掃描點進行均勻加權常規波束形成，可得到波束輸出為

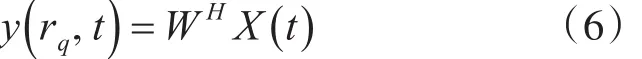
加權向量：

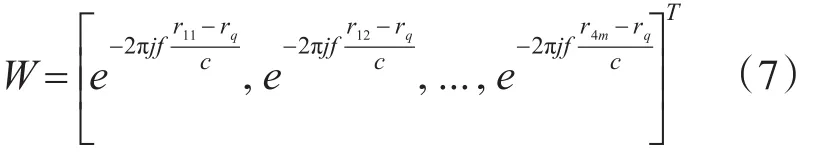
相應rq球面上各個掃描點的輸出功率為

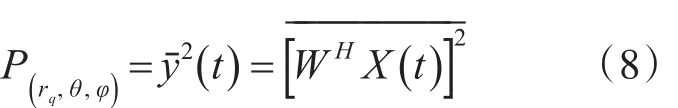
利 用 上 式 ，代 入 不 同 的(θ ，φ ) ，其 中θ=-90°～90°，φ=0°～360°，就可掃描出 rq球面上最大輸出功率，然后通過掃描不同球面rq，得到每個球面的最大輸出功率，通過比較不同球面的最大輸出功率，得到輸出功率的最大值Pmax，其所對應的球面距離即為目標聲源的估計距離r，同時此球面上出現最大輸出功率的掃描點所對應的角度即為目標聲源的方位角和俯仰角。

4 仿真數據檢驗與分析

仿真驗證中假設單條線陣長度d固定為3m，線陣傾斜角度θz為15°，每條子陣上的陣元均勻分布，半徑l1為1.5m，信號采樣頻率 fs為12.5kHz，快拍數為4096，信噪比SNR設為5dB，聲傳播速度c為1500 m/s。每次仿真實驗都進行100次蒙特卡洛實驗。

4.1 陣元數對測距性能的影響

實驗一：假設目標俯仰角為5°，方位角為90°，目標為頻率500Hz的單頻率信號，單條線陣陣元數從3變化到48，目標距離從500m變化到2000m時，目標距離估計相對誤差的三維和二維圖如圖2所示。

從圖2可以看出，單條線陣陣元數對不同距離目標下的距離估計誤差影響比較大，總的來看，陣元數越多，同一距離目標的距離估計就越準確，即測距性能越好。同一陣元數下，目標距離越遠，估計誤差就越大。同時通過取值分析可以得到，當單條線陣陣元數大于30時，2000m范圍內目標的距離估計誤差均小于20%。

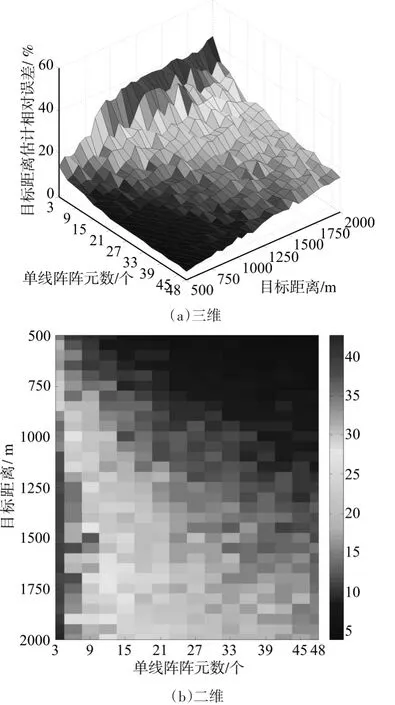
圖2 不同陣元數下的目標距離估計相對誤差

實驗二：假設目標俯仰角為5°，方位角為90°，目標距離為2000m，單條線陣陣元數從3變化到48，目標仍為單頻信號，頻率從500Hz～1500Hz線性變化，不同陣元數下，不同頻率目標的距離估計相對誤差的三維和二維圖如圖3所示。

從圖3可以看出，單條線陣陣元數、信號頻率都是影響距離估計誤差的重要因素，總的來看，陣元數越多，使得同一頻率目標的距離估計越準確，測距性能越好，與仿真實驗一得到的結果一致。另外，同一陣元數下，目標信號頻率越高，距離估計誤差越小。同時通過取值分析可以得到當頻率大于1000Hz時，距離估計誤差可均小于20%。

4.2 陣元數對聚焦空間分辨率的影響

實驗一：假設目標方位角為60°，距離為2000m，信號為頻率500Hz的單頻信號，單條線陣陣元數從3變化到48，目標俯仰角從-90°變化到90°，不同單條線陣陣元數、不同俯仰角下的俯仰角聚焦空間分辨率如圖4所示。

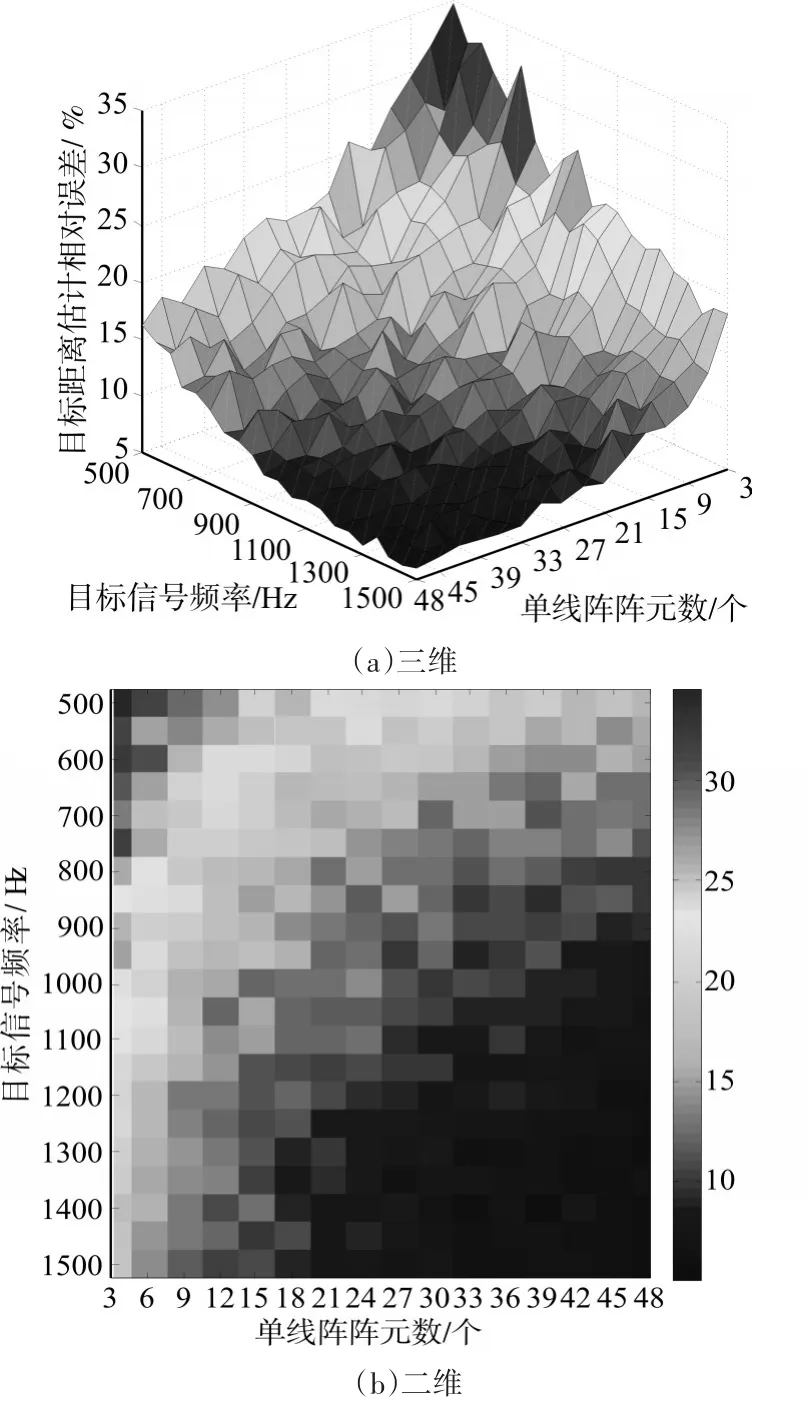
圖3 不同陣元數下的目標距離估計相對誤差

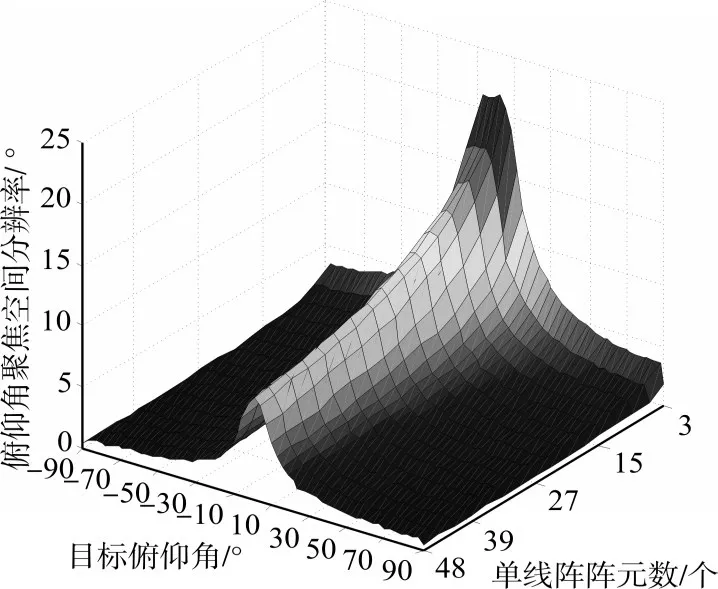
圖4 不同陣元數下的俯仰角聚焦空間分辨率

由圖4可以看到，俯仰角在-15°～15°范圍內的目標，其俯仰角聚焦空間分辨率明顯差于其它位置。對于同一俯仰角的目標，單條線陣陣元數越多，俯仰角聚焦空間分辨率越高，但不是特別明顯。

實驗二：假設目標俯仰角為 5°，距離為2000m，信號為頻率500Hz的單頻信號，單條線陣陣元數從3變化到48，目標方位角從0°變化到360°，不同單條線陣陣元數、不同方位角下的目標方位角聚焦空間分辨率如圖5所示。

從圖5可以看出，單條線陣陣元數越多，目標方位角聚焦空間分辨率越高。同一陣元數下，不同方位目標的聚焦空間分辨率基本相同。通過取值分析，當單條線陣陣元數大于3時，方位角聚焦空間分辨率均小于5°。

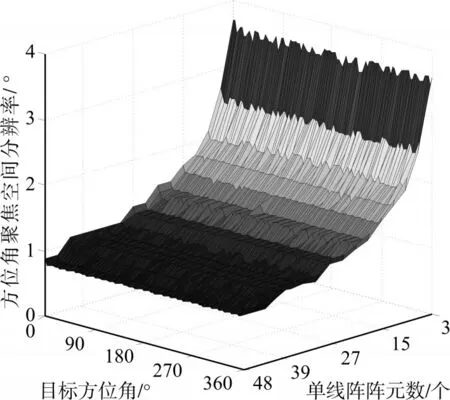
圖5 不同陣元數下的方位角聚焦空間分辨率

實驗三：假設目標距離為2000m，俯仰角為5°，方位角為60°，單條線陣陣元數從3變化到48，目標仍為單頻信號，頻率從500Hz～1500Hz線性變化，不同單條線陣陣元數下，不同頻率目標的俯仰角聚焦空間分辨率如圖6（a）所示，方位角聚焦空間分辨率如圖6（b）所示。

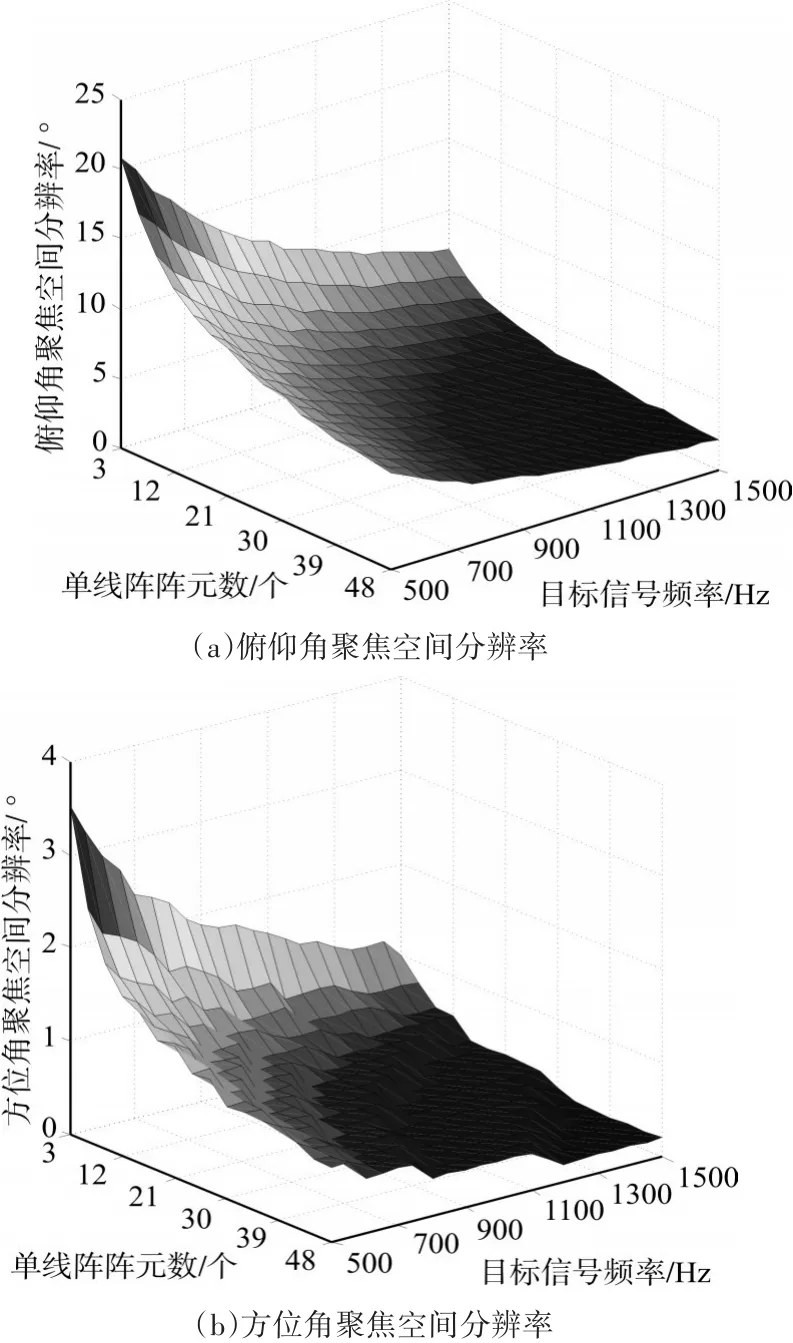
圖6 不同陣元數下聚焦空間分辨率曲線圖

從圖6（a）可以看出，單條線陣陣元數不變，信號頻率越高，俯仰角聚焦空間分辨率值越小，分辨目標能力越強。目標信號頻率不變，線陣陣元數越多，俯仰角聚焦空間分辨率值越小，分辨目標能力越強。通過取值分析，當要求俯仰角聚焦空間分辨率小于5度時，單條線陣陣元數必須多于30個。

從圖6（b）可以看出，單條線陣陣元數不變，信號頻率越高，方位角聚焦空間分辨率值越小，分辨目標能力越強。信號頻率不變，線陣陣元數越多，方位角聚焦空間分辨率值越小，分辨目標能力越強。同時可以看到，方位角聚焦空間分辨率明顯高于俯仰角聚焦空間分辨率，當單條線陣陣元數大于3時，方位角聚焦空間分辨率均小于5°。

綜合圖4～圖6可以看出，總的來說，陣元數越多，對聚焦空間分辨率都有好處，但由尺寸限制，每條線陣的陣元數不可能無限增大，在設計這樣的基陣時，每條線陣上的陣元數應盡可能多。當指標要求方位和俯仰角聚焦空間分辨率均小于5°時，每條線陣上陣元數至少應大于30。

5 結語

本文推導了組合線陣近場信號接收模型和三維聲聚焦波束形成方法，研究了組合線陣近場常規三維聲聚焦波束形成被動定位的性能，從仿真數據分析發現，當固定線陣傾斜角度、線陣與圓心的距離l1和每條線陣的長度時，每條線陣上布設的陣元數對定位性能的影響比較大，陣元數越多，測距性能越好，聚焦空間分辨率越高。當指標要求距離估計相對誤差小于10%，方位和俯仰角聚焦空間分辨率均小于5°時，每條線陣上陣元數至少應大于30個。需要說明的是，本文仿真實驗的目標信號均為窄帶信號，對寬帶目標信號的定位性能還有待進一步分析驗證，同時，組合線陣子陣條數、組合線陣的中心半徑l1、每條線陣的長度等對定位性能的影響也需要進一步研究。