基于最優(yōu)選點(diǎn)數(shù)的多胞LPV建模及其魯棒控制研究*
鄭亞龍 江 駒 徐文螢
(南京航空航天大學(xué)自動(dòng)化學(xué)院 南京 211000)
1 引言
相對(duì)于傳統(tǒng)飛行器,高超聲速飛行器具有飛行包線大、參數(shù)快時(shí)變以及由飛行環(huán)境復(fù)雜等因素造成的參數(shù)強(qiáng)不確定性等特點(diǎn),因此其控制系統(tǒng)必須能夠適應(yīng)較大參數(shù)變化范圍以及大的參數(shù)不確定性。傳統(tǒng)的增益調(diào)參方法設(shè)計(jì)簡(jiǎn)單且容易實(shí)現(xiàn),但大包線內(nèi)的調(diào)參過程極其繁雜,并且無法從理論上保證系統(tǒng)在全包線的穩(wěn)定性和性能指標(biāo)。線性變參數(shù)(Linear Parameter-Varying,LPV)控制是一種新穎的增益調(diào)度技術(shù),克服了傳統(tǒng)增益調(diào)參的控制器插值問題和穩(wěn)定性問題,同時(shí)保證了工程實(shí)現(xiàn)性。
目前,基于LPV的變?cè)鲆婵刂撇呗栽诤娇蘸教祛I(lǐng)域得到了廣泛應(yīng)用[1~4]。針對(duì)全包線控制器的設(shè)計(jì)大多數(shù)采用傳統(tǒng)的增益調(diào)參方法,即采用多個(gè)線性控制器來滿足全包線的控制需求。文獻(xiàn)[5~6]分別按照動(dòng)壓等高線和高度、馬赫數(shù)進(jìn)行包線劃分,其很大程度上依賴設(shè)計(jì)者經(jīng)驗(yàn);另外,傳統(tǒng)的基于Lyapunov函數(shù)的LPV控制方法的凸分解策略和自增益調(diào)節(jié)策略[7~8]采用系統(tǒng)參數(shù)的幾何距離作為依據(jù),無法準(zhǔn)確體現(xiàn)系統(tǒng)動(dòng)態(tài)特性之間的關(guān)系,且在對(duì)象頂點(diǎn)模型求取時(shí)沒有考慮模型的參數(shù)不確定性,控制器魯棒性較差。
基于上述問題,本文提出了一種基于間隙度量的魯棒LPV控制方法,利用間隙度量理論分析得到大包線模型特性變化規(guī)律,指導(dǎo)完成了包線劃分,并根據(jù)包線劃分結(jié)果建立多胞LPV系統(tǒng),同時(shí)考慮高超聲速飛行器模型參數(shù)存在的不確定性,定義不確定多胞LPV系統(tǒng),在此基礎(chǔ)上設(shè)計(jì)魯棒控制器,驗(yàn)證了方法的有效性。
2 高超聲速飛行器的LPV建模問題描述
2.1 模型描述
設(shè)某高超聲速飛行器在平衡巡航飛行條件下的運(yùn)動(dòng)方程為
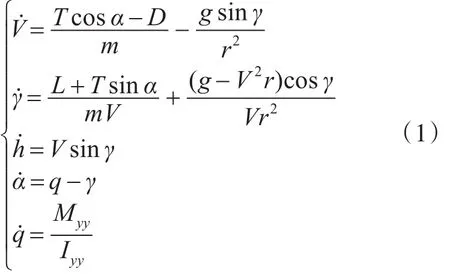
其中:
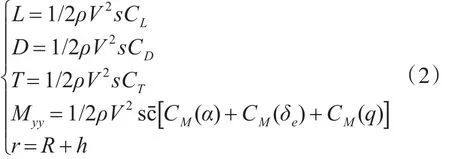
氣動(dòng)參數(shù)表示為
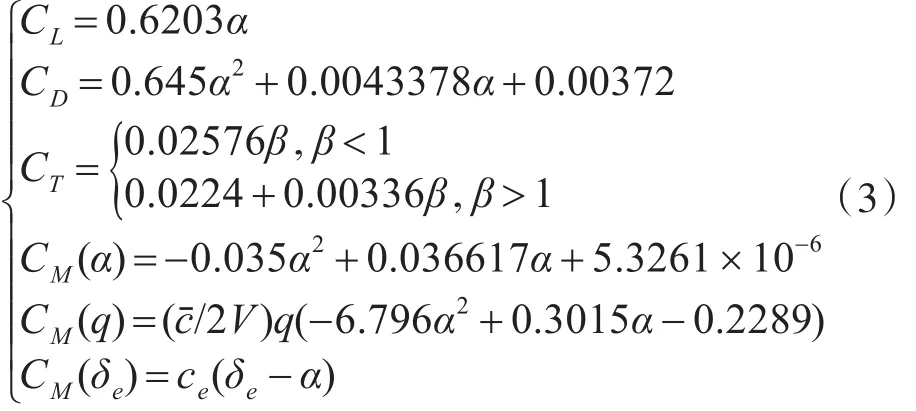
發(fā)動(dòng)機(jī)二階系統(tǒng)模型為
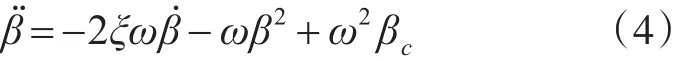
2.2 LPV建模
考慮如下式所示的非線性系統(tǒng):

對(duì)于它的任一個(gè)平衡點(diǎn)采用一階Taylor展開,得到:

式中,fe(x,u)表示系統(tǒng)位于平衡點(diǎn)處的取值,xδ=x-xe,uδ=u-ue,xe和 ue分別表示平衡點(diǎn)狀態(tài)和平衡點(diǎn)輸入。
定義如下偏差變量:Vδ(t)=V(t)-Ve(V,h),其余同理。其中,Ve(V,h)等均為狀態(tài)變量在系統(tǒng)平衡點(diǎn)處的取值,則原運(yùn)動(dòng)方程可表示為

將得到的一系列LTI模型進(jìn)行數(shù)值擬合,即得到高超聲速飛行器的LPV模型,記為
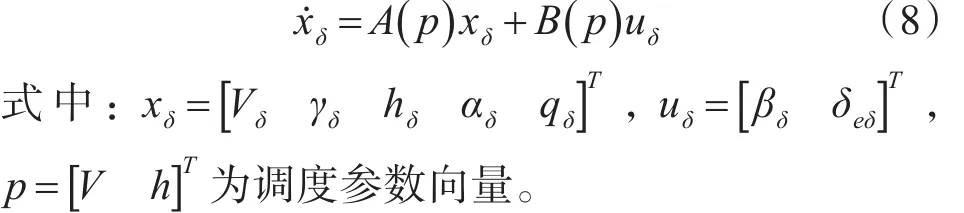
高超聲速飛行器的LPV建模中,主要存在一個(gè)問題,就是如何確定LPV模型平衡點(diǎn)的個(gè)數(shù)。傳統(tǒng)LPV建模中,平衡點(diǎn)的個(gè)數(shù)都是基于經(jīng)驗(yàn)法選取,并沒有統(tǒng)一的標(biāo)準(zhǔn)和理論依據(jù)。因此需要確定一個(gè)平衡點(diǎn)的選取準(zhǔn)則,在同時(shí)考慮建模精確度和計(jì)算復(fù)雜度的情況下確定一個(gè)最優(yōu)的平衡點(diǎn)選取個(gè)數(shù)。
下面引入間隙度量理論,確定最優(yōu)的平衡點(diǎn)個(gè)數(shù),進(jìn)而建立LPV模型。
3 基于最優(yōu)選點(diǎn)數(shù)的多胞LPV建模
3.1 間隙度量理論概述
間隙度量理論由Zames和El-Sakkary引入到控制領(lǐng)域中,目的是更精確地描述線性系統(tǒng)之間的差異程度。
定義 1[9~10]設(shè) G1,G2∈ Rn×m(s)是具有 m 個(gè)輸入 n個(gè)輸出的傳遞函數(shù)陣,(D1,N1)和(D2,N2)分別為G1和G2的規(guī)范右互質(zhì)分解,則G1和G2之間的間隙度量為
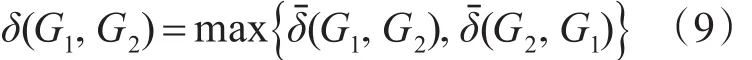
式中
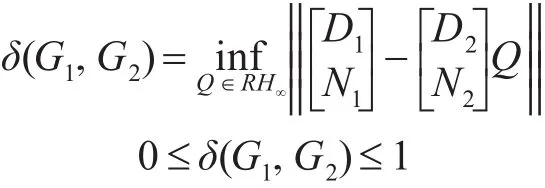
由間隙度量的定義,如果δ接近于0,則表明兩個(gè)系統(tǒng)動(dòng)態(tài)特性近似。因此,間隙度量值的大小可反映模型變化的大小,依此可作為飛行包線劃分的依據(jù)。
為了更加清晰地顯示間隙度量值的物理意義,我們得到如下間隙度量值的變化曲線,如圖1~圖2。
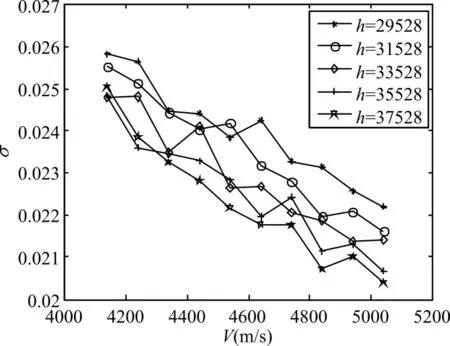
圖1 相同高度下間隙度量值變化曲線

圖2 相同速度下間隙度量值變化曲線
從上圖可以看出,盡管是相同的速度間隔或者高度間隔,但相鄰兩平衡點(diǎn)之間的間隙度量值并不一樣,即有必要依據(jù)間隙度量值選取平衡點(diǎn)個(gè)數(shù)。
3.2 建立優(yōu)化模型
將系統(tǒng)的間隙度量理論引入到LPV建模過程中,從而定量的描述模型之間的差異程度,更好地選取平衡點(diǎn)的個(gè)數(shù)。
但同時(shí)考慮到,平衡點(diǎn)的個(gè)數(shù)同樣影響著控制器的計(jì)算復(fù)雜度,因此,結(jié)合一般的針對(duì)LPV模型的控制器設(shè)計(jì),對(duì)線性矩陣不等式(LMI)的計(jì)算復(fù)雜度進(jìn)行分析。根據(jù)文獻(xiàn)[11],求解LMI的計(jì)算復(fù)雜度為Ncost=O(n2m2N+nm3N),其中,n表示狀態(tài)空間的維數(shù),m表示系統(tǒng)矩陣的塊對(duì)角元素的個(gè)數(shù)。因?yàn)閚和m皆為已知常數(shù),所以線性矩陣不等式的運(yùn)算復(fù)雜度與平衡點(diǎn)的個(gè)數(shù)為一次線性關(guān)系。
按照當(dāng)前系統(tǒng)與頂點(diǎn)系統(tǒng)的間隙度量值最小和計(jì)算復(fù)雜度最低的指標(biāo)對(duì)系統(tǒng)LPV建模平衡點(diǎn)個(gè)數(shù)進(jìn)行優(yōu)化,建立優(yōu)化目標(biāo)函數(shù)如下:
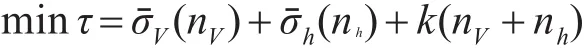
式中,nV,nh分別表示速度和高度方向上劃分的平衡點(diǎn)的個(gè)數(shù),σˉ表示間隙度量平均值,k為權(quán)系數(shù),統(tǒng)一前后兩部分的量級(jí)。
取不等式約束為

具體的優(yōu)化策略如下:
對(duì)于任意的平衡點(diǎn)選取個(gè)數(shù)nV×nh,計(jì)算所有相鄰頂點(diǎn)之間的間隙度量值;
對(duì)符合不等式約束的nV,nh,最優(yōu)平衡點(diǎn)選取個(gè)數(shù)可由式(10)優(yōu)化得到。
實(shí)踐證明“導(dǎo)游天下”APP、云班課平臺(tái)將視頻學(xué)習(xí)、課堂討論、測(cè)驗(yàn)、互動(dòng)評(píng)價(jià)等教學(xué)方式與課前、課中、課后的教學(xué)過程融為一體,有效組織了整個(gè)課程教學(xué)的實(shí)施,輕松解決教學(xué)難點(diǎn),保障學(xué)習(xí)的效果和實(shí)用性。“教”與“學(xué)”的每個(gè)步驟和結(jié)果經(jīng)平臺(tái)記錄,形成課程“大數(shù)據(jù)”,其分析結(jié)果可與以往教學(xué)情況做比較,有效指導(dǎo)教師教學(xué)和學(xué)生學(xué)習(xí),使“教”與“學(xué)”有的放矢、事半功倍,充分體現(xiàn)信息化學(xué)習(xí)的強(qiáng)大優(yōu)勢(shì)。動(dòng)畫游戲等信息資源的使用,將知識(shí)技能融為一體,讓教學(xué)變得節(jié)能高效。
3.3 建立基于最優(yōu)選點(diǎn)數(shù)的LPV模型
選取高超聲速飛行器速度變化范圍為4090.3m/s~5090.3m/s ,飛 行 高 度 變 化 范 圍28528m~38528m,取權(quán)系數(shù)k=0.01,圖3給出優(yōu)化函數(shù)的變化曲線。
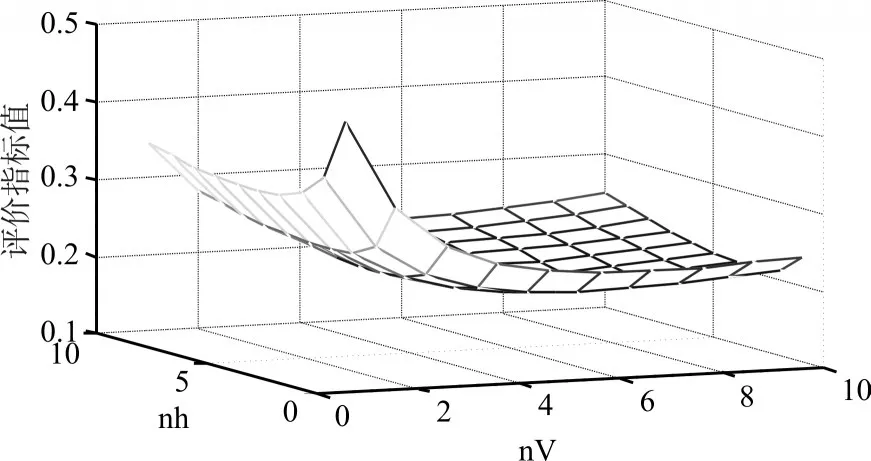
圖3 評(píng)價(jià)指標(biāo)隨平衡點(diǎn)個(gè)數(shù)的變化曲線
最終我們得到優(yōu)化結(jié)果為nV=3,nh=6,即在速度方向上劃分為3個(gè)速度值,高度方向上劃分為6個(gè)高度值,包線內(nèi)共得到18個(gè)平衡點(diǎn)。通過第一節(jié)介紹的雅可比線性化方法,可以得到18個(gè)標(biāo)稱點(diǎn)以及相應(yīng)的18個(gè)LTI系統(tǒng)(狀態(tài)矩陣可表示為(Ai,Bi,Ci,Di),i=1,2,…,18),對(duì)上述LTI進(jìn)行插值擬合,最終可得到高超聲速飛行器LPV模型:
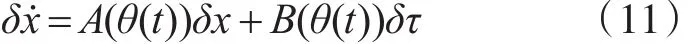
3.4 仿真分析
為了驗(yàn)證我們所建立的LPV模型的有效性,在速度變化范圍4090.3m/s~5090.3m/s,飛行高度變化范圍28528m~38528m內(nèi)任取一點(diǎn),將基于最優(yōu)選點(diǎn)數(shù)的LPV模型,以及傳統(tǒng)LPV模型,與非線性模型在該點(diǎn)的平衡狀態(tài)的雅可比線性化矩陣進(jìn)行伯德圖比較。
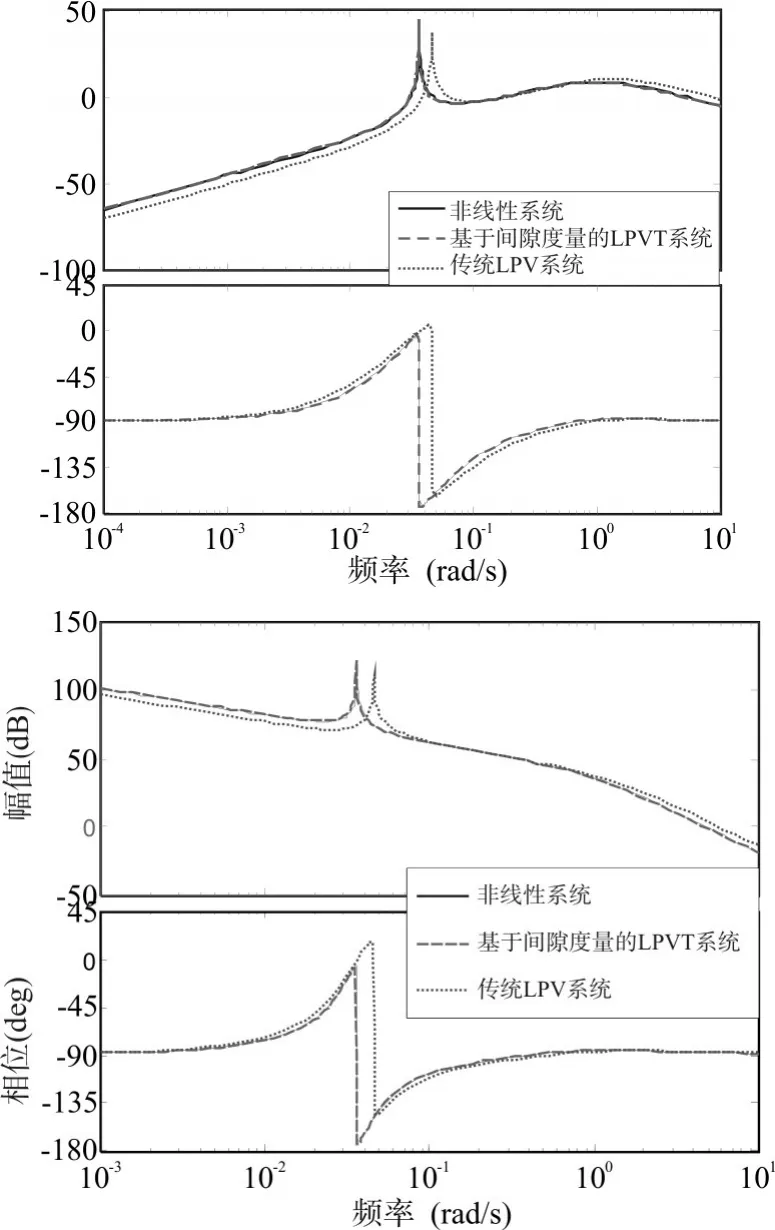
圖4 LPV系統(tǒng)與非線性系統(tǒng)伯德圖比較
仿真可以看出,基于最優(yōu)選點(diǎn)數(shù)建立的LPV系統(tǒng)的伯德圖曲線與原始非線性系統(tǒng)在該點(diǎn)線性化后的伯德圖曲線基本吻合,而傳統(tǒng)LPV建模得到的伯德圖則與其存在一定偏差。這表明由最優(yōu)選點(diǎn)數(shù)建立的LPV系統(tǒng)可以更好地復(fù)現(xiàn)原始非線性系統(tǒng)的特性。
為了進(jìn)一步說明該建模方法有效性,對(duì)基于最優(yōu)選點(diǎn)數(shù)建立的LPV模型進(jìn)行魯棒控制器設(shè)計(jì)。
4 魯棒控制器設(shè)計(jì)
4.1 控制問題描述
針對(duì)上一節(jié)建立的LPV模型(11)首先進(jìn)行多胞轉(zhuǎn)化:設(shè)緊集 Pθ??3n:θ∈Pθ,?t>0可以看作是一個(gè)由凸包定義的多胞型:
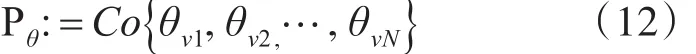
式中N為頂點(diǎn)個(gè)數(shù)。通過定義上述多胞型,系統(tǒng)就可以用頂點(diǎn)處LTI模型的線性組合來表示,也就是多胞LPV模型

我們的目的就是要尋找一個(gè)常數(shù)矩陣K∈?n×2n,使得反饋控制輸入:

能使閉環(huán)系統(tǒng)漸近穩(wěn)定。
4.2 不確定性分析
事實(shí)上,由于線性近似誤差和其他的一些不確定項(xiàng),頂點(diǎn) Pi:=(Ai,Bi),i=1,2,…,N 存在參數(shù)不確定性。

式中,(Aˉi,Bˉi)是在 N 個(gè)不同的點(diǎn)計(jì)算得到的標(biāo)稱頂點(diǎn)。盡管通過增加頂點(diǎn)個(gè)數(shù)N,可以更加逼近系統(tǒng)的非線性特性,但同時(shí)也增加了計(jì)算復(fù)雜度和一些沒必要的計(jì)算。
根據(jù)式(14)和LPV描述式(13),閉環(huán)系統(tǒng)可以表示為
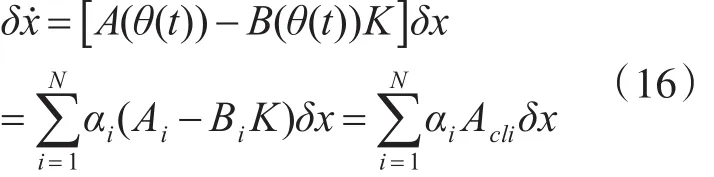
定義Δi為第i個(gè)頂點(diǎn)閉環(huán)模型處的參數(shù)不確定性:

將不確定性式(15)代入式(16),系統(tǒng)變成如下形式:
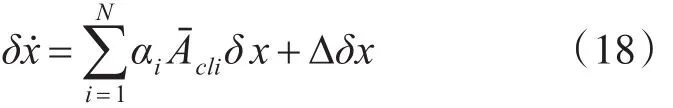
式中:

是第i個(gè)頂點(diǎn)模型的標(biāo)稱系統(tǒng)矩陣。

可以看作是整個(gè)閉環(huán)系統(tǒng)的多胞參數(shù)不確定性。
定義1 將包含參數(shù)不確定性Δ的多胞系統(tǒng)式(19)稱為不確定多胞LPV系統(tǒng)。
定義2 如果滿足任意頂點(diǎn)處的不確定性不超過與其他頂點(diǎn)之間的距離,則稱該系統(tǒng)是多胞主導(dǎo)的。即
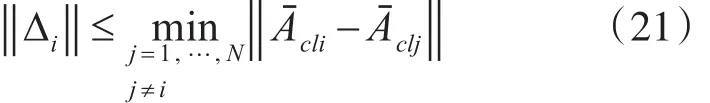
4.3 魯棒控制器設(shè)計(jì)
基于以上條件,在接下來的定理中給出了系統(tǒng)式(18)魯棒穩(wěn)定的充分條件。
定理1不確定多胞LPV系統(tǒng)是漸近穩(wěn)定的,當(dāng)且僅當(dāng)存在正定對(duì)稱的矩陣 X=XT>0,Y=YT>0,以 及 M 使 得 對(duì) 所 有 的i∈{1,2,…,,M},滿足下面的LMIs:
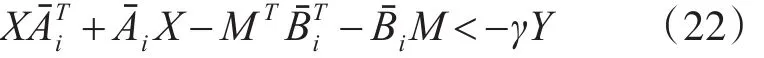
對(duì)足夠大的γ有
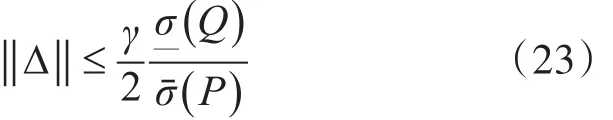
其中Q=X-1YX-1,P=X-1。如果存在這樣的解,則控制器的增益可以寫成:

5 仿真實(shí)驗(yàn)
對(duì)高超聲速飛行器巡航段進(jìn)行仿真驗(yàn)證。設(shè)計(jì)仿真條件:高超聲速飛行器初值V0=4590m/s,h0=33528m,指令信號(hào)為Vc=40m/s,hc=60m,得到速度和高度的變化曲線。過程中給飛行器模型加入一定的參數(shù)攝動(dòng),分別假設(shè)大氣密度ρ的攝動(dòng)|Δρ|/ρ0=0.03 、俯 仰 力 矩 慣 性 積 Iy的 攝 動(dòng)|ΔIy|/Iy0=0.03、俯仰力矩系數(shù)中的參數(shù)ce的攝動(dòng)|Δce|/ce0=0.03、翼弦長(zhǎng) c的攝動(dòng) | Δc|/c0=0.03。對(duì)比分析考慮參數(shù)不確定性和未考慮參數(shù)不確定性情況下兩種控制器的仿真效果,如圖5~圖6所示。
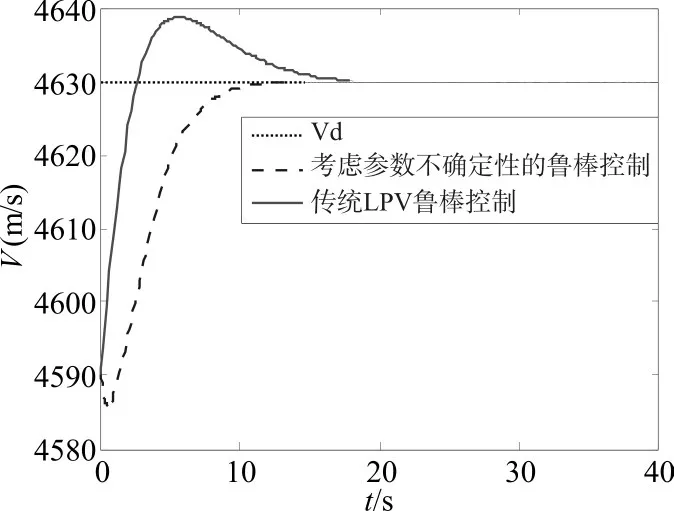
圖5 速度變化對(duì)比曲線
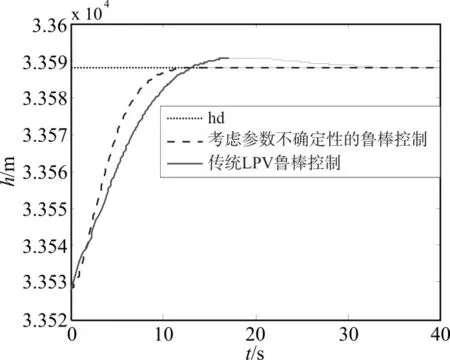
圖6 高度變化對(duì)比曲線
由圖5和圖6可以看出,在建立LPV模型過程中,考慮頂點(diǎn)模型的參數(shù)不確定性,設(shè)計(jì)出來的魯棒控制器具有更好的動(dòng)態(tài)跟蹤性能,驗(yàn)證了算法的正確性。
6 結(jié)語
1)間隙度量的理論被應(yīng)用到LPV建模過程中,建立了高超聲速飛行器縱向模態(tài)的多胞LPV模型,在同時(shí)考慮平衡點(diǎn)個(gè)數(shù)和控制器復(fù)雜度的情況下,設(shè)計(jì)了優(yōu)化模型,解得最優(yōu)的選點(diǎn)數(shù),并基于此設(shè)計(jì)多胞LPV模型。基于最優(yōu)選點(diǎn)數(shù)的多胞LPV建模相比于傳統(tǒng)的建模方法保守性更低小,大包線內(nèi)系統(tǒng)性能更趨于一致,也有利于降低飛行器控制系統(tǒng)設(shè)計(jì)的保守性;
2)在求取多胞頂點(diǎn)模型時(shí)充分考慮模型參數(shù)的不確定性,使得基于不確定多胞LPV模型設(shè)計(jì)的魯棒控制器具有更好的性能,在高超聲速飛行器存在較大參數(shù)不確定性的情況下仍能保證系統(tǒng)的穩(wěn)定性。

