基于支持度函數的2D雷達目標高度估計方法*

楊軍佳 時銀水 王世軍 黃沈華

（陸軍炮兵防空兵學院鄭州校區 鄭州 450000）

1 引言

自從第二次世界大戰以來，雷達在戰爭中的作用越來越重要。為了獲取目標比較精確的位置信息，通常需要對目標的三維坐標進行測量。雖然在裝備更新換代的過程中，三坐標體制的雷達逐步替代老舊體制的2D雷達，但是2D雷達并不是沒有任何用武之地。為了能夠獲取目標的三維信息，一些學者利用兩坐標雷達的測量參數對目標的三維坐標進行了有益的探索。文獻［1］針對等高度飛行、高信噪比的目標，闡述了利用兩坐標雷達獲取的目標幅度和距離變化信息進行測高的原理，對波束形狀和錄取數據數量等因素的影響進行了分析。文獻［2］利用目標的動態模型，結合兩坐標雷達關于目標多個時刻的測量信息，對目標三維空間的位置進行最大似然估計。文獻［3］針對兩坐標雷達組網系統誤差估計忽略了目標高度影響的問題，采用模塊化方法，將3部兩坐標雷達組網分成平面與空間兩個模塊進行目標高度與系統誤差的聯合估計。文獻［4］從集中式框架下融合中心的廣義量測方程出發，推導了融合中心的更新方程，并用各部兩坐標雷達的局部跟蹤信息代替更新方程中的量測，從而得出目標3維狀態的估計。文獻［5］針對雷達普遍存在距離和角度量測系統誤差工程實際情況，以及兩坐標雷達目標高度可觀測分析和估計技術缺乏對雷達系統誤差考慮不足之處，利用Fisher信息矩陣，通過求解CRLB下限，對系統誤差下的兩坐標雷達目標高度可觀測分析問題進行了深入研究。文獻［6］以目標恒海拔等速運動為前提，利用協同單元提供的目標指示信息，對兩坐標雷達的空間目標高度問題進行了研究。文獻［7］針對彈載雷達平臺不穩定的情況下，分析了寬波束比窄波束測高的優勢以及3種不同算法測高精度的對比。文獻［8］利用兩部2D雷達的局部估計建立關于目標高度所產生系統誤差的非線性模型，進而采用UKF濾波方法實現對目標的實時估計。文獻［9］根據雷達天線的“仰角-增益”測試數據，利用目標點跡屬性中的高低波束增益差，估算目標高度信息。文獻［10］分析了不同位置、目標高度條件下幾何量測理論誤差，并利用濾波算法對目標高度進行工程化應用。

以上文獻所提方法為解決目標高度估計問題提供了一定的思路。本文考慮采用多部2D雷達組網的方式，利用不同雷達測量同一目標的冗余信息，實現對目標高度的融合估計，以提供目標的三維坐標信息。

2 理論分析

2.1 高度估計可行性分析

圖1為雷達與目標三維位置關系示意圖。其中，點A表示其中一部雷達，其坐標為；點B表示另外一部雷達，其坐標為；點C表示目標，其坐標為；點 D 是目標在XOY平面上的投影，其坐標為；點 D'是點B向CD作垂線，且與CD的交點，其坐標為；點 E 是過點 D 向 X 軸作垂線，且與X軸的交點，其坐標為；點 E'是過點 D'向過B點且與X軸平行的線作垂線，且與該線的交點，，其坐標為；雷達 A 對目標 C 的測量距離為rA、測量方位角為α，雷達B對目標C的測量距離為rB、測量方位角為β。

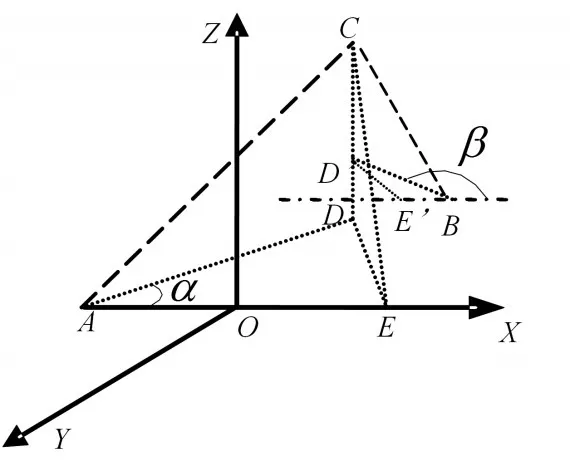
圖1 雷達與目標三維位置關系示意圖

從上面的描述中，可以得到：

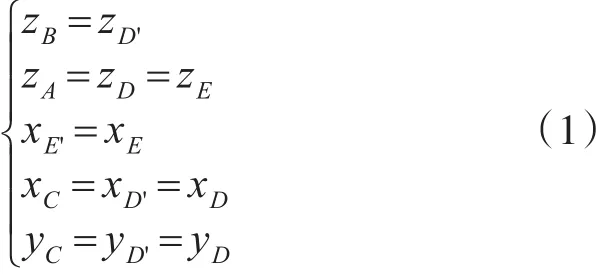
從圖1中雷達與目標之間的位置關系，可以得到：

將式（1）代入式（2）可得：

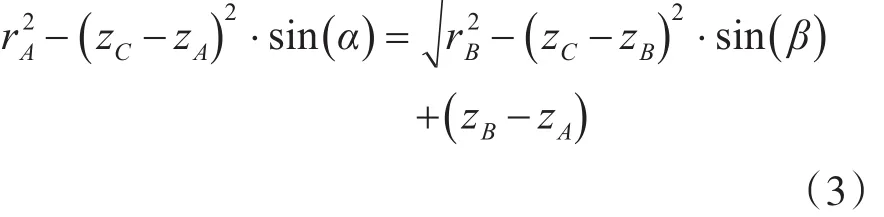
在式（3）中，由于 rA、α、rB、β以及 zA、zB為已知參數，則可計算出zC的值。

2.2 高度數據融合估計

由于雷達對目標距離和方位角的測量存在誤差，導致式（3）計算出的目標高度也存在誤差。為了提高目標高度估計精度，將n部雷達兩兩組合計算的個目標高度值進行加權融合，以減小距離和方位角測量誤差的影響。

由于修正證據距離是在Jousselme距離的基礎上進行的改進，不僅保留了Jousselme距離良好的數學特性，而且解決了其在衡量證據相似性上所存在的問題，并且收斂性更好［11］，因此，本文考慮以任意兩部雷達組合估計的目標高度之間的修正證據距離來確定不同高度估計值之間的融合權值。

假設第 i、j（1≤i＜j≤n）部雷達對目標高度的估計值為 hij，第 j、k（1≤j＜k≤n）部雷達對目標高度的估計值為hjk，則依據文獻［12］可得hij和hjk之間的修正證據距離為

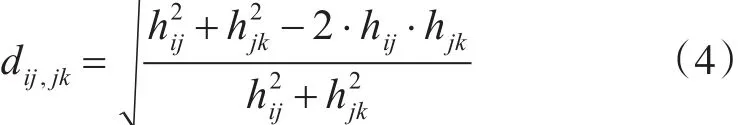
式（4）中 dij，jk越小，表明高度估計值 hij和 hjk之間的差異越小。

定義1 兩高度估計值之間的相互支持度為兩高度估計值之間修正證據距離的倒數，即：

式（5）中 d'ij，jk越大，表明兩高度估計值之間的相互支持程度越高，目標高度真實值越接近hij和hjk。

依據上述分析，可以構建n部雷達任意兩部組合計算出的目標高度值之間的相互支持度矩陣D：

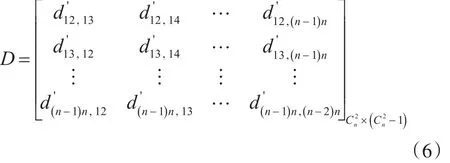
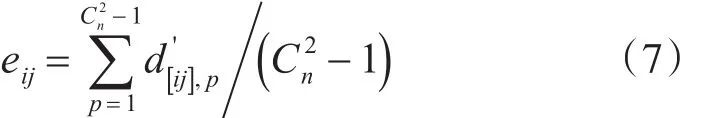
從式（7）中可以看出，任意兩部雷達組合估計的目標高度值與其余-1個高度估計值之間的一致支持度越大，該兩部雷達組合估計的目標高度值可信度越高，其在高度融合估計中所占的比重應該越大。

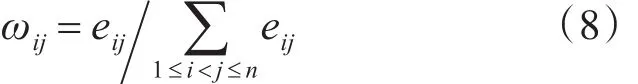
依據式（9）可得n部雷達對目標的高度融合估計值為：

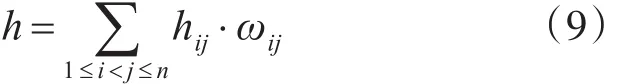
3 雷達組網高度估計方法

依據上述分析，在采取半自動錄取目標參數的情況下，利用多部雷達對同一目標參數測量的冗余信息估計目標高度值的方法為

步驟一：所有測量數據時空對準

假設第i部雷達在ta時刻測量的目標參數為時刻測量的目標參數為，則tc時刻的目標參數為

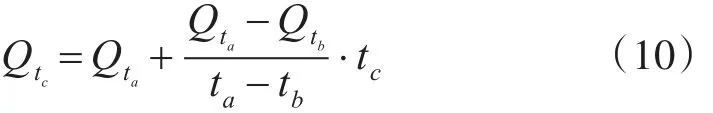
在進行參數測量信息時空對準的時候，盡量以采樣間隔比較大的參數測量時間為基準，以減小因時空對準引入較大的誤差。

步驟二：依據式（3）計算同一時刻n部雷達中任意兩部雷達組合的個高度估計值。

步驟三：依據式（4）、（5）、（6）構建 n 部雷達任意兩部組合計算出的目標高度值之間的相互支持度矩陣D。

步驟四依據式（7）計算任意兩部雷達組合估計的目標高度值與其余-1個高度估計值之間的一致支持度。

步驟五依據式（8）計算任意兩部雷達組合估計的目標高度值在個高度估計值融合中所占的比重。

步驟六依據式（9）進行n部雷達對目標高度的融合估計。

4 仿真分析

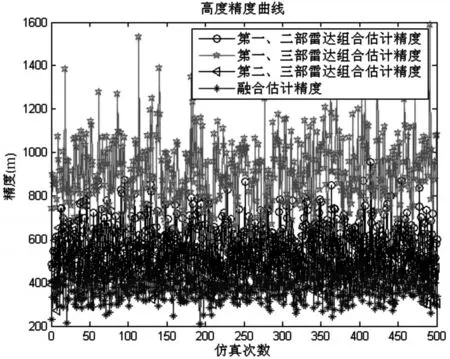
圖2 500次仿真高度估計精度

從圖2及圖3可以看出：

1）采用任意兩部雷達都能夠對目標的高度信息進行估計，但是估計精度不同。雖然第二和第三部雷達組合的高度估計精度優于第一和第二部雷達組合的高度估計精度，但是兩者的高度估計精度相差不大；第二和第三部雷達組合以及第一和第二部雷達組合的高度估計精度明顯優于第一和第三部雷達組合的高度估計精度。主要原因是第一和第二部雷達以及第二和第三部雷達距離和方位測量精度的偏差一樣，都明顯小于第一和第三部雷達的距離和方位測量精度的偏差。

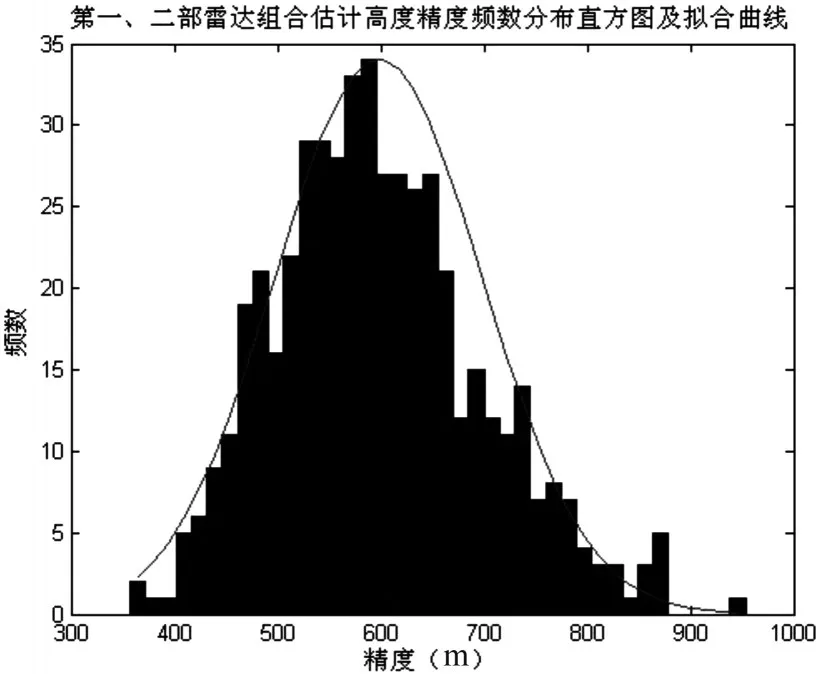
圖3 （a）第一、二部雷達組合估計高度精度頻數分布直方圖及擬合曲線

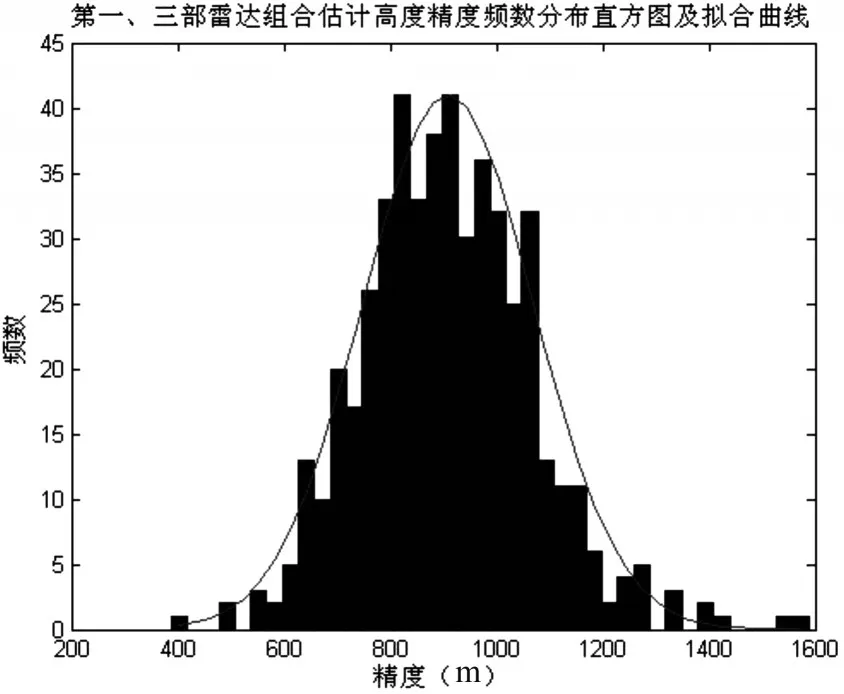
圖3 （b）第一、三部雷達組合估計高度精度頻數分布直方圖及擬合曲線

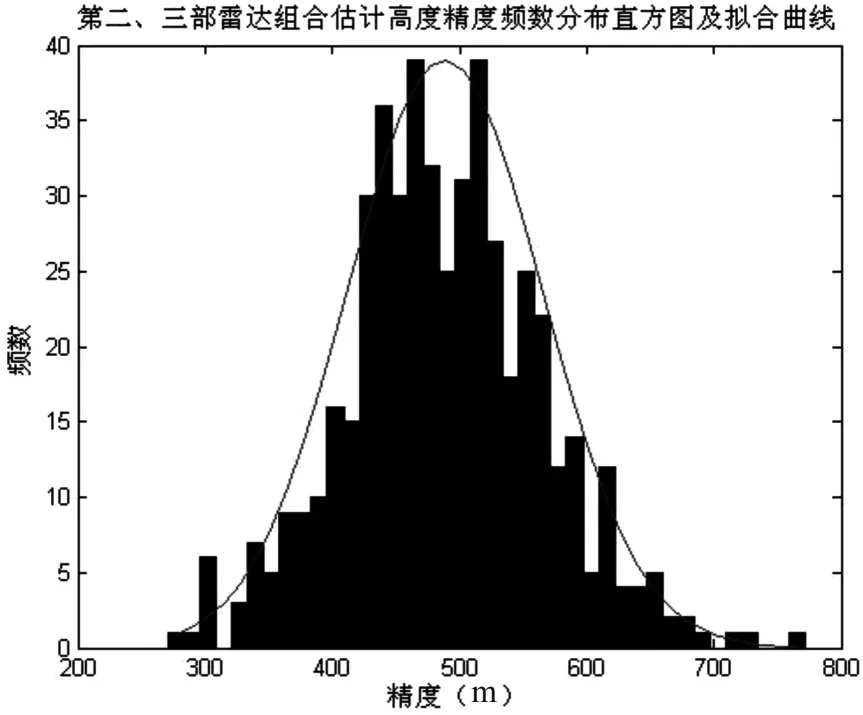
圖3 （c）第二、三部雷達組合估計高度精度頻數分布直方圖及擬合曲線

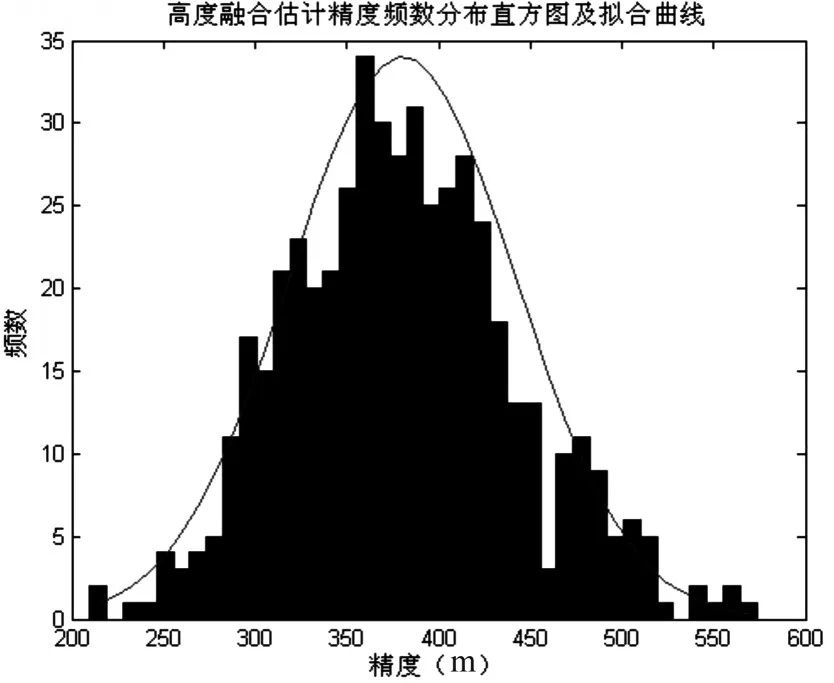
圖3 （d）高度融合估計精度頻數分布直方圖及擬合曲線

2）進行加權融合后的高度估計精度明顯優于任意兩部雷達組合對目標的高度估計精度。主要原因是依據越靠近真實值的數據出現的概率應該最大的大數定律，通過計算不同高度值之間的一致支持度，比較科學地確定不同高度值參與融合的權重。

5 結語

通過對2D雷達組網進行目標高度估計的分析和討論，可以得出：

1）采用兩部雷達對目標高度估計的時候，盡量使用距離和方位測量精度相差不大的兩部雷達，最好是同型號的雷達；

2）為了提高目標高度的估計精度，可以采用多部雷達組網的方式。

但是在采用雷達組網方式的時候，必須考慮估計精度的提高程度與部署雷達數量的關系，必須找到一個合適的臨界值，這也是本課題接下來需要研究的內容。